基于特征频率筛选的声发射信号去噪算法

陈文峰， 向华， 许光达， 柯西江

（1.华中科技大学 机械科学与工程学院，武汉430070; 2. 国家数控系统工程技术研究中心，武汉430070）

0 引言

刀具的状态与加工的质量一直是机床领域的关注的焦点，而声发射（Acoustic emission，AE）技术作为对应力作用状态监测的一种手段，在刀具磨损监测和加工质量监控领域发挥着重要的作用。AE本质是材料应变能以弹性波的形式释放[1-3]，所以大应力作用下的去除成形将产生大量的AE事件[3]。同样的，机械传动的过程是应力在多个对象间的传递，也会产生一定的AE事件。所以在复杂加工环境中，采集的原始AE信号（以下简称原始AE信号）包含了非加工产生的AE信号（以下简称非加工信号）与加工产生的AE信号（以下简称加工信号）。为获得清晰的加工信号，需对原始信号进行去噪。

非加工信号源有：机床自身、机床内部的液压与气压系统、机械运动过程的撞击及所有摩擦过程[4]。非加工信号主要由加工外的应力作用产生，非加工信号与加工信号的性质相似，在频域上均分布在100 kHz～1 MHz[5]。但非加工信号源的位置与传感器间存在多种不同的介质，传感器采集的信号实际已在各类介质中发生多次界面反射、干涉与衰减，且属于介质模态频率分量的信号会被增强，最终在100 kHz～1 MHz的频谱中表现为散布的多个高能峰，进一步可以将这类频率概括为一种离散的频率分布，并将这些频率视为该分布的特征频率，而加工信号在频域具有为低幅值、宽频带的特点，进一步可以概括为一种连续频率分布[6-7]，如图1所示。

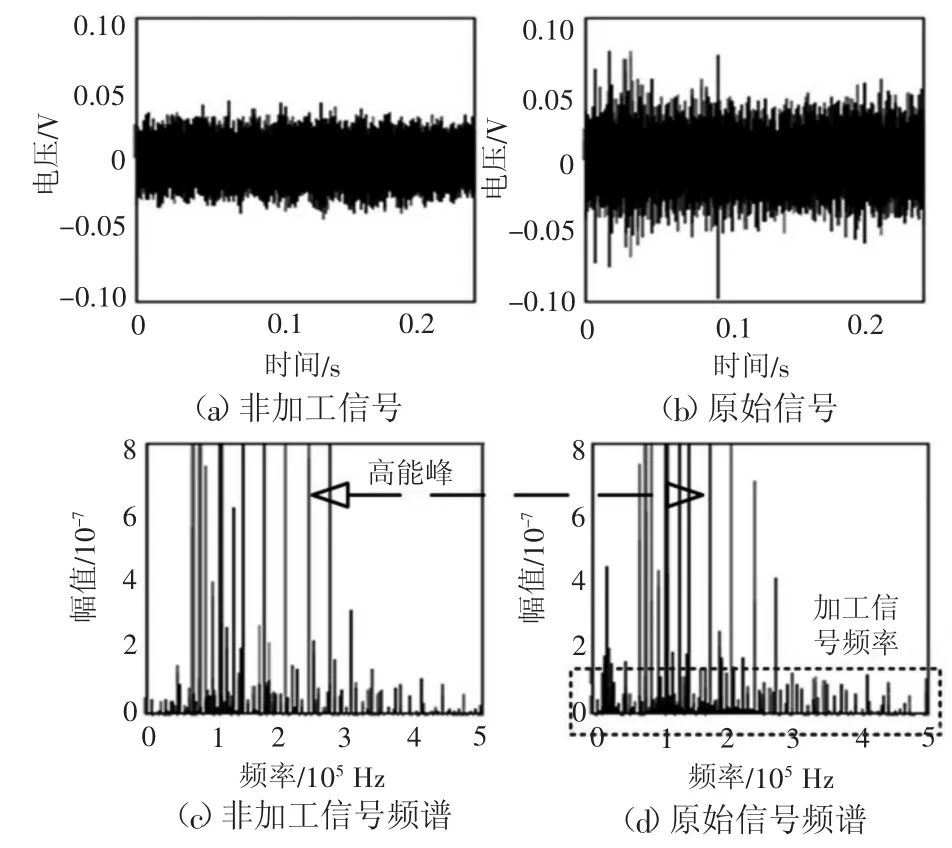
图1 离散频率分布与加工信号频率示意图

早期受限于计算机性能，对原始信号中加工信息的提取以RMS滤波、振铃计数等硬件手段为主[1,7]，无法处理非加工信号的干扰。近几年，随着计算机的处理性能的发展，在加工领域中，声发射分析技术逐渐从参数法分析法转向频域与时频域分析[3,8-9]。对非加工信号也逐渐在频域与时频域进行研究，X.Chiementin等[10]对于轴承的AE信号，分别对自适应滤波方法（Self-Adaptive Cancellation，SANC）、谱减法与小波降噪方法进行实验与分析，得出自适应滤波方法降噪效果最佳的结论。王宗炼等[11]、程铁炼等[12]、王雨虹等[13]、李占国等[14]均采用小波包降噪的方法对原始信号进行去噪。而王丽华等[15]则基于自动编码器无监督网络去除非加工信号。上述对非加工信号处理算法的研究，取得了一定的进展与效果，但均停留在实验室阶段，加工环境理想、信号清晰，并且未结合非加工信号离散频率分布的特点，在面对复杂的实际加工环境时，对原始信号的去噪效果十分有限。但结合离散频率分布特点，使用通用的带阻滤波方式，由于加工信号宽频带的特点，将损失阻带边沿加工信号的频率分量。

对此，本文根据非加工信号离散频率分布的特点，提出基于特征频率筛选的去噪算法——DCFS。并与自适应滤波算法与带阻滤波算法进行去噪效果比较，DCFS具有最优的去噪性能。本文将在第1节中，介绍DCFS算法的原理与实现方法，第2节介绍实验方法与实验结果的分析与比较，第3节对非加工信号的特点及DCFS进行总结。

1 基于特征频率筛选的去噪算法

将机床空运行时AE信号视为非加工信号，以便对非加工信号的特点进行直观的观察，实际机床的原始信号与非加工信号及其频谱如图1所示。根据图1中（c）～（d）的频谱分布关系，可以直观地发现，非加工信号频谱存在多个分散的高能峰，且在原始信号频谱中依旧存在，而原始信号本身在低幅值处存在连续的频率分布，该频率分布只出现在加工过程中。对此可以得出，非加工信号是一种离散频率分布的信号，并且该频率分布在加工过程中依然存在，而加工信号在低幅值处具有较为连续的频率分布。

DCFS算法结合上述离散频率分布的特点，将离散分布的频率视为非加工信号的特征频率，以这些特征频率的频率大小与幅值为依据，对原始信号进行去噪，具体可概括为两个子方法：基于去噪特征频率窗口滑动的频谱筛选方法、基于iFFT的去噪信号重构方法。算法的总的流程与效果如图2所示。

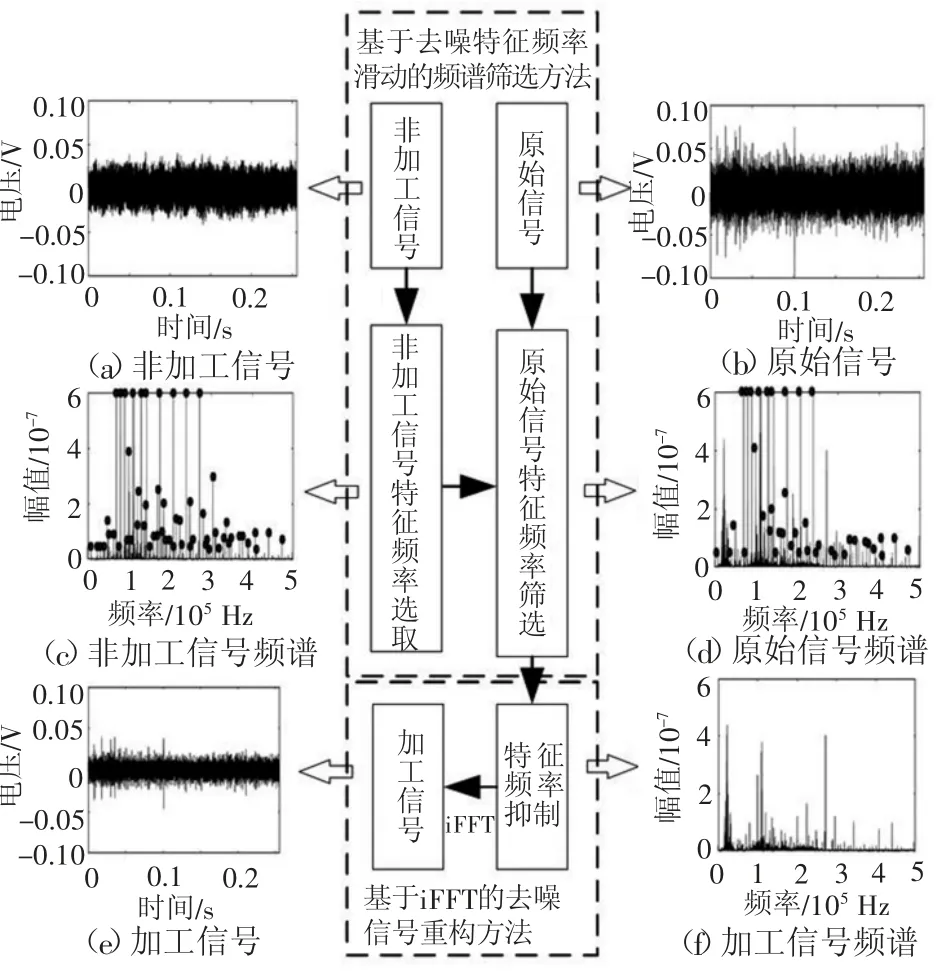
图2 DCFS流程与效果示意图

1.1 基于去噪特征频率窗口滑动的频谱筛选方法

基于去噪特征频率窗口滑动的频谱筛选方法，可以分为两个步骤：非加工信号特征频率选取与原始信号特征频率筛选与抑制。因为需要进行频率选取，所以需通过快速傅里叶变换（FFT）获得频谱序列，FFT的核心离散傅里叶变换公式如下，并换算出幅值能量与相位：

其中：N为离散信号点数；Y（ω）为幅值能量；phase（v）为相位。

非加工信号特征频率选取需结合离散分布的频率的高能峰特点，为了确定频率分布中高能频率与低能频率分界幅值，本步骤先对非加工信号进行FFT，得到幅值Y，并对其进行降序排列获得Ydes与其差分Ydes′，保留Ydes和Ydes′与频率值的映射关系，通过设定的阈值，确定幅值变化放缓的临界点。视该临界点为高低能分量的幅值分界点，根据映射关系确定高幅值的频率集合Fpeak：

该步骤算法为提取特征频率集合，

输入为非加工信号x(n)，输出为特征频率集合Fpeak、特征频率幅值Ypeak。具体流程为：1）开始；2）加载非加工信号x(n)；3）[F,Y]= FFT(x(n))←FFT获得频率与对应幅值；4）Ydes(n)=Y↓、Ydes′(n)=Ydes(n+1)- Ydes(n)←Y(n)降序排列并差分；5）Fpeak=[F|Ydes(F)＞1×10-9；|Ydes′(F)|＞1×10-11]，Ypeak=Y(Fpeak)←确定特征频率；6）结束。

各阶段操作流程与效果如图3所示。

原始信号特征频率筛选与抑制则根据已获得特征频率集合Fpeak中的各元素的频率值，循环对原始信号频谱对应的区域进行筛选。本步骤将以Fpeak的频率值为中心，在原始信号频谱中构建正负方向、长度可调的窗口。结合特征频率幅值大、离散分布的特点，通过窗内的幅值分布情况，判断该窗内是否存在近似的特征频率。

图3 非加工信号特征频率选取示意图

若不存在特征频率，则不进行抑制；若存在近似特征频率，则根据窗内非特征频率的幅值分布关系，利用最小二乘（Least squares，LSQ）多项式拟合方法，确定抑制后特征频率的幅值大小。最小二乘多项式拟合方法如公式（4）、公式（5）：

式中：多项式基函数选择｛1，x，…，xm｝；xi为非特征频率；yi为非特征频率幅值；wi为权函数，本算法取1；φ（x）为拟合多项式函数，多项式系数｛a0，a1，…，am｝为方程（4）的解。

将特征频率带入φ（x）即获得抑制后特征频率处的幅值。经过循环，最终获得去噪后的加工信号的频率分布关系。输入为原始信号xoriginal(n)、特征频率集合Fpeak、特征频率幅值Ypeak，输出为加工信号频率幅值Ymanu、相位Phase。具体算法流程为：1）开始；2）加载原始信号xoriginal(n)；3）F(ω) =FFT(xoriginal(n)) phase=arctan(Re(F)/IM(F))，Y=||F||←FFT获得频率与对应幅值和相位；4）i=1，N=size(Fpeak)；5）当i＜N；6）Yw=Y(Fpeak(i)±L)，Fw=Fpeak(i)±L←构建长度为2L的窗体；7）Ywdes=Y↓Ywdes′= Ywdes(n+1)-Ywdes(n)←降序排列窗内幅值；8）判断窗内是否存在||Ywdes′||＞1×10-8，不存在开启下一次循环←判断是否存在离散分布的特征频率；9）Fwpeak=[F| ||Yw(F)-Ypeak(Fpeak(i))||＜1×10-8] ←筛选窗内高能分量；10）Fwpeak是否为空，若空则至14；11）Fleave=[F|F∈Fwpeak(n)&&F∈Fw(i)]，Yleave=Y(Fleave)←确定窗内非特征频率及幅值；12）=LSQ(x=Fleave，y=Yleave)←最小二乘拟合幅值分 布关系；13）Y(Fwpeak)=←确定特征频率抑制后幅值大小；14）i=i+1；15）结束循环；16）Ymanu=Y←保留抑制后的加工信号频率幅值；17）结束。

算法示意图如图4所示。

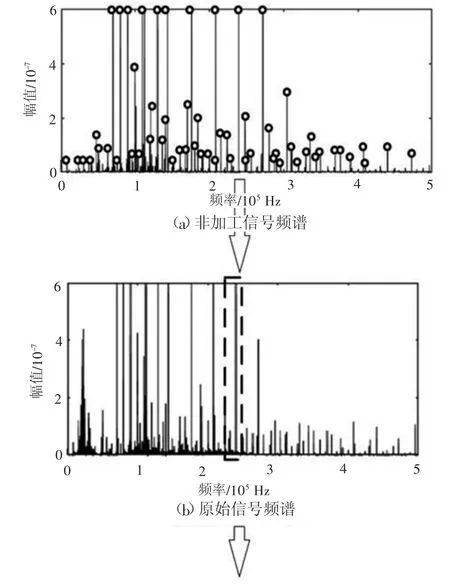
图4 原始信号特征频率筛选与抑制示意图

1.2 基于iFFT的去噪信号重构方法

对于抑制后的频谱图结合原始信号的频率相位信息，结合关系公式:

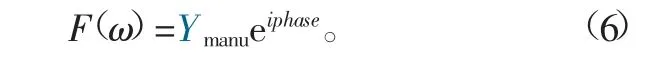
使用新构建的复信号进行快速傅里叶逆变换，获得原始信号中的加工信号，该信号重构流程示意图如图5所示。

离散快速傅里叶变换公式为

图5 信号重构示意图

DCFS受常规谱减法的启发设计而成，但是在该应用场景中，离散频率分布的频率幅值并不是固定的，常规谱减法无法处理频率幅值存在一定波动的情况，同时无法保留被抑制频率分量中加工信号的分量。对此结合离散频率分布的特征频率的特点，设计了上述的DCFS算法，在保留原始信号中加工信号分量的同时，有效抑制了非加工信号的分量。

2 DCFS实验验证

为了验证DCFS的实际去噪效果，本实验在实际工厂的加工环境下进行实验，采集非加工状态与加工状态时的数据，对数据使用DCFS进行去噪，并与LMS-自适应滤波算法和带阻滤波算法进行比较。

2.1 实验设备与方案

本文采用的实验设备与器件主要为：kistler 5125C声发射信号调理仪，kistler 8152C声发射传感器，NI-9223电压采集卡，白钢与钨钢φ10直柄立铣刀，尺寸规格为15 mm×60 mm×160 mm的6063铝合金、45钢、7075铝合金。

实验在常温下Z540B铣床上进行，对工件一侧进行同方向循环面铣削，将回程空运行作为非加工信号。采集卡采样频率1MSPS，传感器信号调理仪自带50～500 kHz带通滤波器。为贴近实际生产加工中声发射传感器的使用方式，将声发射传感器安装在通用夹具一侧。实验装置连接示意图如图6所示。为验证算法的适用性，采集了不同刀具及不同材料情况下的加工与非加工信号。具体实验方案如表1所示，共计180组数据。

2.2 实验结果

图6 实验设备连接拓扑图

表1 实验参数

对采集数据使用DCFS对数据进行去噪，对比180组数据的结果，去噪算法生成的加工信号保留了原始信号中加工分量的声发射信息，非加工声发射信号被抑制。部分实验结果如图7～图9所示。

2.3 算法比较分析

为了与其他算法进行比较，需设定一个可量化指标对去噪效果打分，但实际情况中无法获知原始信号中的真实加工信号或者真实的非加工信号，不能采用常规的功率类评价指标，如信噪比（SNR）、均方根差（RMSE）。对此本文采用归一化互相关函数最大值（以下简称互相关值）作为两信号关联程度的判定。互相关函数峰值采用如下公式：

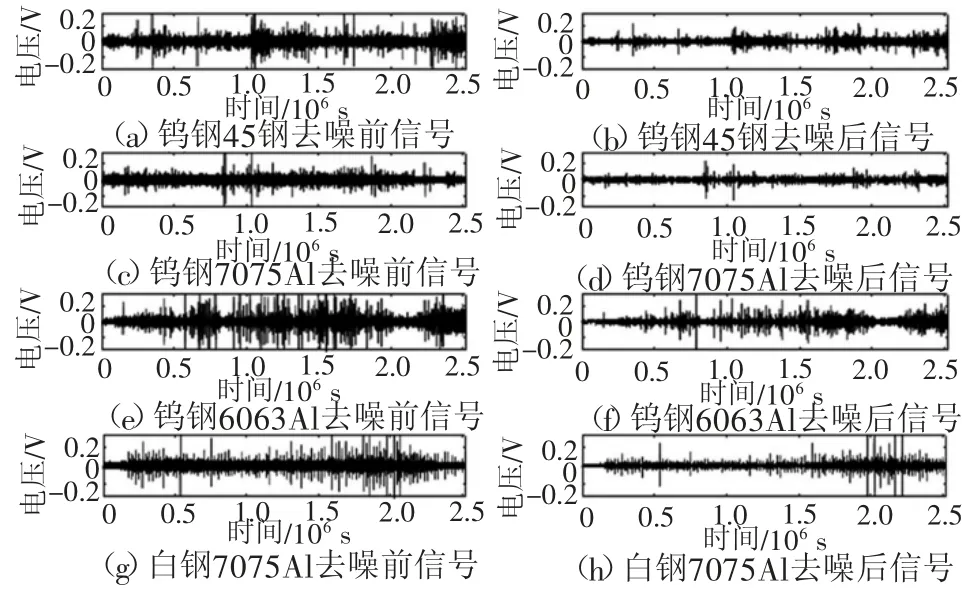
图7 各参数第一组1刀去噪前后数据对比图

其中：x，y为输入信号；N为信号长度；R^xx（0）和R^yy（0）分别为x与y的自相关函数值。式（9）中的最大互相关值表示两信号相关性，若关联性越大，则值越大。使用加工信号与原始信号的互相值及加工信号与非加工信号的相关值值作为去噪效果的评判依据，要求前者保持一个较高的值，而后者应为低的值。

图8 各参数第二组8刀去噪前后数据对比图

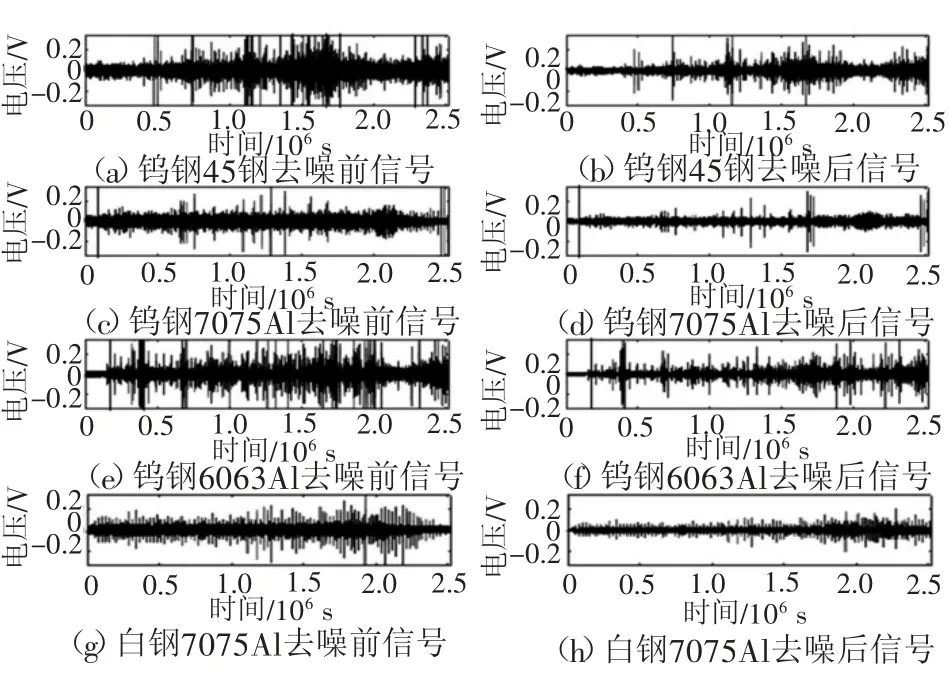
图9 各参数第三组15刀去噪前后数据对比图

为比较DCFS的去噪效果，对所有数据分别使用LMS-自适应滤波、DCFS、带阻滤波。对结果进行相关性分析，以加工信号与非加工信号相关值作为横坐标，以加工信号与原始信号相关值作为纵坐标，构建二维结果分布图，最终结果如图10所示。根据相关值的评价指标要求可得出，图中越位于右下角则去噪效果越好，越位于左上角则去噪效果越差。

根据图10所示，DCFS相比于LMS-自适应滤波算法与带阻滤波算法，180组数据均处在图像右下角，针对不同刀具与不同材料均表现出了良好的去噪效果，在3种算法中去噪能力最佳。带阻滤波结果集中在图像左上角，去噪效果在三者中最差，验证了前文对于带阻滤波去噪过程中损失阻带边沿加工信号能量的论述。LMS-自适应滤波则与原始信号存在着极高的相关性，与非加工信号也存在较高的相关性，去噪能力有限。

3 结语

本文将实际机床采集的声发射信号作为研究对象，以频谱分析为工具，对机床中非加工声发射信号的特点进行了分析，发现该信号是一种离散频率分布的信号，并提出了一种有效的去噪方法，具体得出了以下两点结论：

1）经实验数据验证，提出铣削机床中加工声发射信号的非加工分量在频域中呈现散布的多个高能峰，具有一种离散的频率分布的特点，且在机床运行过程中持续存在。本文视高能峰为特征频率，在采集的180组数据中，特征频率值始终保持在相同频率上。这些特征频率为进一步进行去噪算法的设计与铣削加工状态分析提供基础。

2）结合非加工信号的离散频率分布的特点，设计了基于特征频率筛选的去 噪 算法——DCFS。该方法在保留铣削中加工声发射信号分量的前提下，有效抑制了非加工信 号。 经180组数据测试，去噪效果稳定，且优于通用的带阻滤波方法与LMS-自适应滤波方法。该算法能有效适应嘈杂的加工环境，提升了声发射技术在复杂工厂应用的可能性，为进一步开发刀具状态监测与加工质量监控提供了清晰的信号。

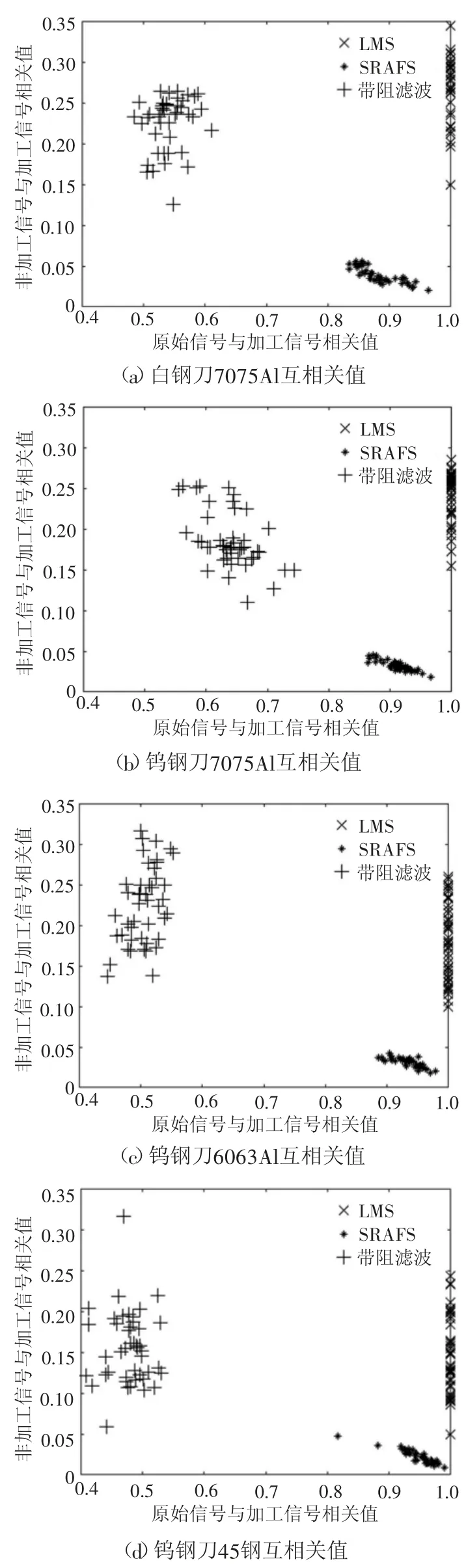
图10 各数据非加工信号-加工信号/原始信号-加工信号相关值分布图