400 km/h动车组车体压力载荷列车参数影响特征研究

徐银光 王志钧 魏 康 梅元贵 李 艳

(1.中铁二院工程集团有限责任公司， 成都 610031；2.兰州交通大学甘肃省轨道交通力学应用工程实验室， 兰州 730070)

随着行车速度的不断提高，高速列车所面临的空气动力学问题日益显著，其不仅对列车的运行环境、经济性等造成影响，更影响着车内人员的安全和乘坐舒适感。高速列车通过隧道时，空气动力学问题更加严重[1]，由于空气的可压缩性和隧道壁面的空间限制，列车头部和尾部驶入隧道时产生的压力波以近似当地声速的速度在隧道内传播并发生反射，形成了隧道内复杂的压力环境，并使车外压力发生剧烈变化[2]，严重时可能会危害到列车的运行安全，并造成车内人员耳感不适等问题。气动载荷的反复作用还会使车体结构及隧道衬砌等部件产生疲劳破坏[3]。

当前，国内外对于列车隧道空气动力学的研究方法主要有现车试验、模型试验和数值模拟3种[4]。20世纪 60年代以来，日本、英国、法国、德国等国家研究了高速列车隧道压力波的形成机理和影响因素[5-7]，基于相关研究，各国对不同速度等级下的铁路隧道压力波效应提出了相关标准[8-12]，为列车的气动性能设计和运行维护提供了技术支持。隧道压力波数值研究方法主要有基于CFD软件的三维流动模型和基于特征线的一维流动模型方法。模拟列车隧道压力波的三维流动模型方法主要有面元法、有限体积法和有限元法，可模拟出车体不同部分的流场情况及气动载荷，但其计算成本较高、计算周期较长。一维数值模拟方法可高效、大批量地模拟出不同隧道及列车参数的隧道压力波，且已证实与现车试验和模型试验结果吻合较好，可满足工程设计要求，为不同列车参数的车体气动载荷、车内人员舒适性等设计及优化提供可靠依据[13]。

目前，400 km/h及以上高速铁路已进入研发阶段[14]，为对该速度等级下的列车隧道气动载荷问题进行研究，本文采用发展成熟的一维非定常可压缩不等熵流动模型特征线数值模拟压力波方法，开展400 km/h速度等级下，单列车通过隧道和隧道中央等速交会时的压力波形成机理以及不同列车编组长度和列车速度对车外压力幅值影响规律的研究，归纳车体压力载荷的基本分布特征，论证车外压力幅值与列车速度平方成正比的适用条件和范围，为今后深化研究压力载荷变化提供基础。

1 研究方法

由于空气与列车壁面、隧道壁面之间存在摩擦、传热等不可逆因素，列车通过隧道时，隧道内的空气流动为伴有边界层分离的三维非定常不等熵紊流流动。因隧道长度远大于隧道断面水力直径，列车长度也远大于列车与隧道形成的环状空间横截面的当量水力直径，故隧道压力波在隧道断面上的传播时间远小于压力波在隧道长度和列车长度方向上的传播时间。对于一定长度的隧道和列车而言，隧道断面上的压力可近似相等，隧道断面上的空气流速可近似为常数。因此，可将隧道内的空气流动简化为一维非定常不等熵流动模型，并利用特征线方法求解控制方程，最终求得车外压力。具体求解方法及控制方程可参见文献[5]。

2 计算结果和分析

2.1 列车隧道内诱发压力波形成机理

单列车(8节编组)以400 km/h通过长度为 400 m的隧道时，列车运行轨迹和隧道内压力波反射叠加如图1(a)所示。头车车外压力时间历程曲线如图1(b)所示。

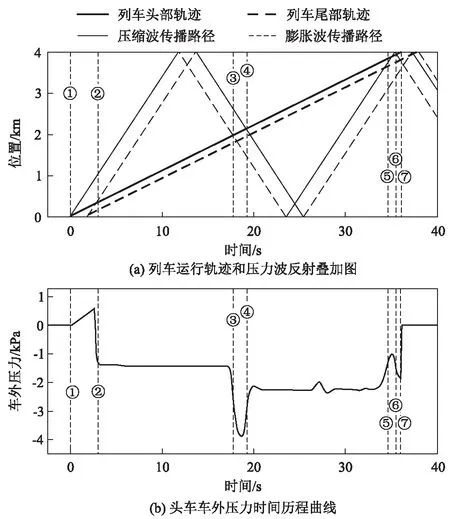
图1 单列车通过隧道时压力波形成机理示意图

由图1可知：

(1)列车头部于①时刻驶入隧道并压缩空气形成压力增量，产生了初始压缩波；列车尾部于②时刻驶入隧道并由于隧道空间突然增大形成负压，产生了初始膨胀波；列车头尾车驶出隧道时也将产生压缩波和膨胀波。压缩波和膨胀波在隧道内以近似当地声速的速度向隧道另一端传播，到达隧道端口后，压缩波和膨胀波分别转化成相反形式波形反射回隧道入口端，循环往复，形成了隧道内复杂的压力环境。

(2)压缩波和膨胀波传播到达头车外部时，分别引起头车车外压力的急剧升高和降低，且由于隧道壁面的摩擦，不同时刻的车外压力变化量有所减小。

(3)单列车通过隧道时，头车外部压力受到列车进入隧道产生的压缩波和膨胀波以及其反射波的影响；隧道中央等速交会时，头车外部压力除受到自身进入隧道产生的压力波的影响外，还会受到对向列车进入隧道产生的压力波的影响以及不同形式波形在隧道内叠加使车外压力变化量增大或减小的影响和列车交会对车外压力产生的影响。故隧道中央等速交会时车外压力的变化比单列车通过隧道时车外压力的变化更为复杂。

2.2 列车编组长度的影响

定义系数K为最大正压值、最大负压值、最大压力峰峰值16节编组和8节编组的比值，分析不同编组长度车外压力的差异。由参考文献[10]给出的最不利隧道长度的估算公式可知，速度100～500 km/h所对应的最不利隧道长度约为 1 100～1 200 m，故本文在进行列车编组长度和列车速度影响特征研究时，隧道长度均取为 1 200 m，隧道净空面积取100 m2。8节编组(210 m)和16节编组(420 m)列车以400 km/h单列车通过隧道和隧道中央等速交会情形下，头、中、尾车的车外最大正压值、最大负压值和最大压力峰峰值的变化规律分别如图2和图3所示。

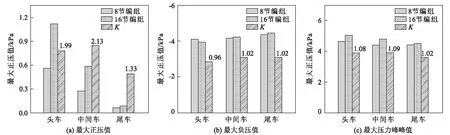
图2 单列车通过隧道情形下车外压力幅值变化规律图

图3 隧道中央等速交会情形下车外压力幅值变化规律图

由图2、图3可知：

(1)除单列车通过隧道情形下，16节编组头车最大负压值较8节编组列车较小外，其他头、中、尾车的最大正压值、最大负压值和最大压力峰峰值，16节编组均较8节编组列车更大。

(2)两种编组最大正压值和最大压力峰峰值的差异从头车到尾车有逐渐减小的趋势，最大负压值差异由头车到尾车有逐渐增大的趋势。

(3)隧道中央等速交会的情形下，两种编组的最大正压值、最大负压值和最大压力峰峰值的差异均比单列车通过隧道时更大。

(4)两种编组车外最大正压值的差异最大，车外最大压力峰峰值次之，最大负压值的差异最小，故编组长度对车外最大正压值的影响最显著，对车外最大负压值的影响最小。

2.3 列车速度的影响

选取8节编组(210 m)列车以100～500 km/h速度通过长度为 1 200 m隧道(隧道净空面积为100 m2)为计算条件，研究单列车通过隧道和隧道中央等速交会情形下车外压力随列车速度的变化规律。单列车通过隧道和隧道中央等速交会情形下，头车外最大正压值、最大负压值和最大压力峰峰值随列车速度的变化如图4、图5所示。

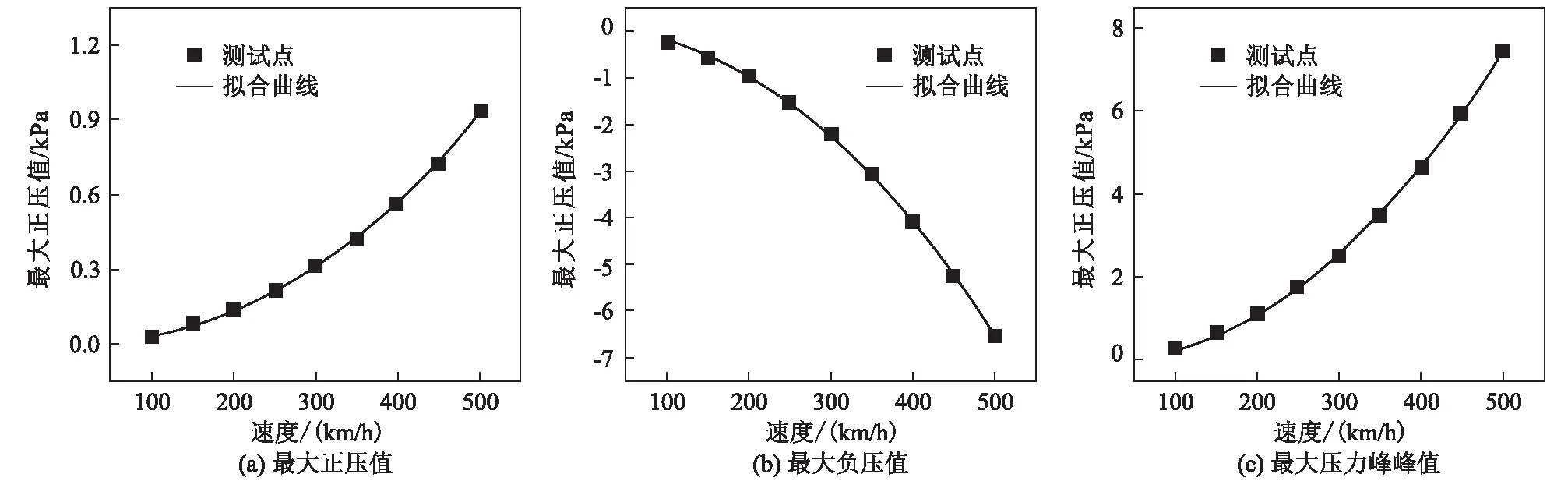
图4 单列车通过隧道情形下头车外压力幅值随列车速度的变化曲线图

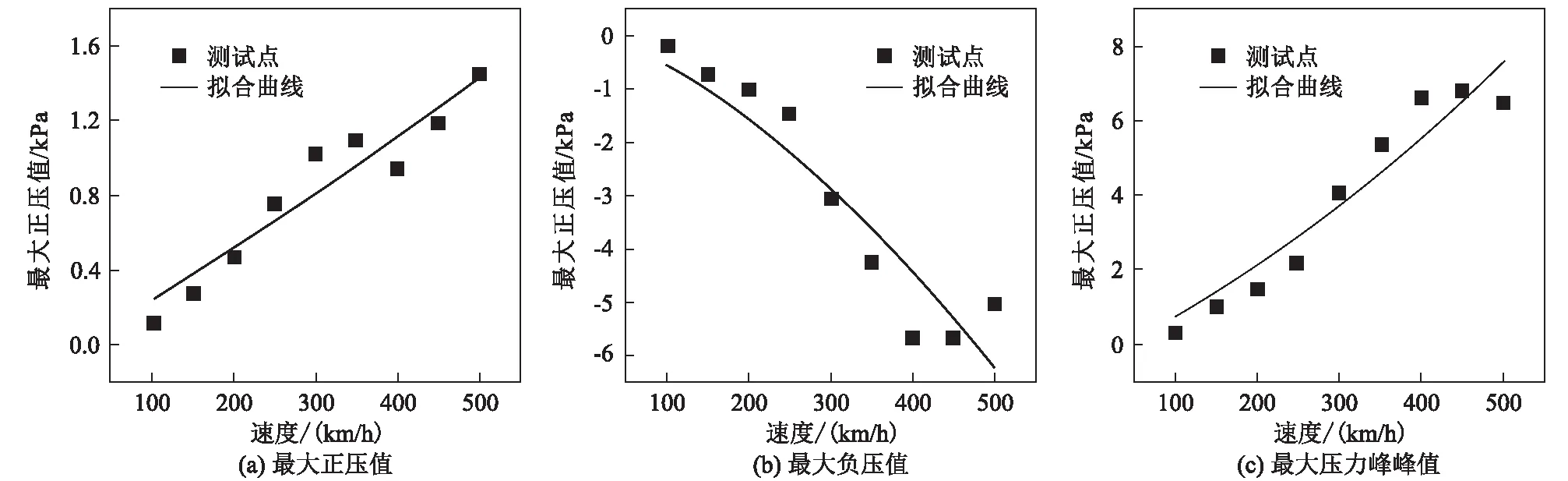
图5 隧道中央等速交会情形下头车外压力幅值随列车速度的变化曲线图

为更直观地反映两者的变化规律，将不同速度下的车外最大正压值、最大负压值和最大压力峰峰值分别按式(1)形式拟合：

Δp=AVB

(1)

式中：A——拟合函数系数；

V——列车速度，取100～500 km/h；

B——列车速度的拟合指数。

单列车通过隧道和隧道中央等速交会情形下的曲线拟合参数及平均拟合误差如表1、表2所示。

表1 单列车通过隧道拟合参数表

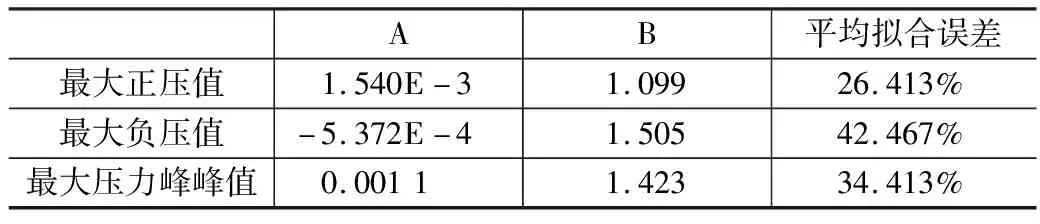
表2 隧道中央等速交会拟合参数表

由综合分析可知：

(1)单列车通过和隧道中央等速交会情形下，车外最大正压值、最大负压值和最大压力峰峰值随速度的增大而增大，并与列车速度的B次方近似成正比。

(2)单列车通过隧道情形下，拟合曲线各点的拟合误差较小；隧道中央等速交会情形下，拟合曲线各点的拟合误差则较大。两种不同情形下，拟合函数系数A总体保持在10-6～10-3数量级，指数B的取值总体保持在1～2.5之间。

(3)单列车通过隧道情形下，系数A绝对值的取值范围为1.4×10-6～1.7×10-5；隧道中央等速交会情形下，系数A绝对值的取值范围为0.5×10-3～1.6×10-3。由此可认为，隧道长度为 1 200 m时，隧道中央等速交会的系数A绝对值较单列车通过隧道时要大。

(4)单列车通过隧道情形下，指数B保持在2左右；隧道中央等速交会情形下，指数B的取值则介于1～1.6之间。由此可认为，隧道长度为 1 200 m时，隧道中央等速交会情况下的指数B的取值小于单列车通过隧道情形，且单列车通过隧道情形下，车外最大正压值、最大负压值和最大压力峰峰值近似与速度的平方成正比。

为论证单列车通过隧道时，车外最大正压、最大负压和最大压力峰峰值与列车速度平方成正比的适用性，选择不同隧道长度，对列车通过隧道时，头车外最大正压值、最大负压值和最大压力峰峰值随列车速度变化的拟合参数进行探究，隧道长度范围为250～1 700 m。列车以100 ～500 km/h速度单列车通过隧道和隧道中央等速交会情形下，头车外最大正压值、最大负压值和最大压力峰峰值随列车速度的变化规律拟合为式(1)所示函数时，拟合指数B随隧道长度的变化规律如图6、图7所示。

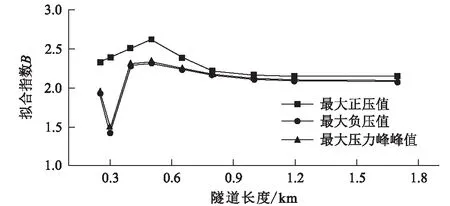
图6 单列车通过隧道情形下拟合指数B随隧道长度的变化曲线图

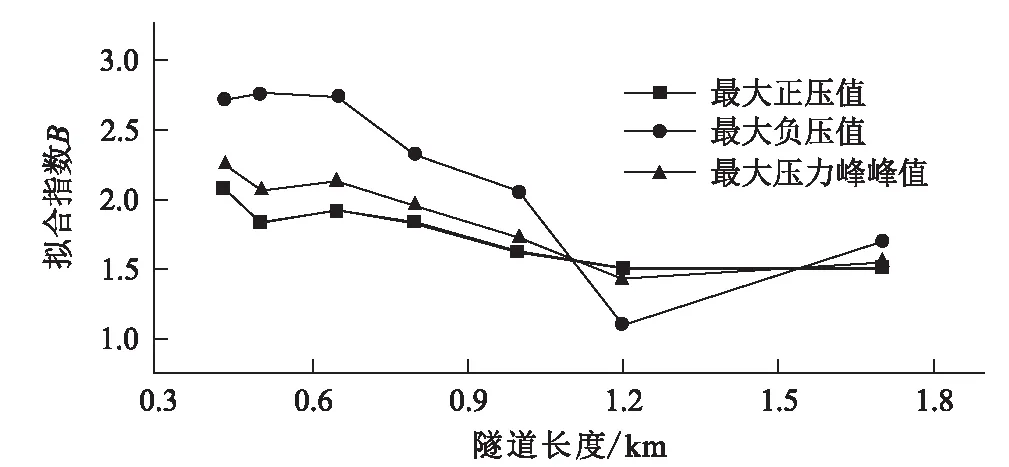
图7 隧道中央等速交会情形下拟合指数B随隧道长度的变化曲线图

由图6、图7可知：

(1)单列车通过隧道情形下

①头车外最大正压值关于列车速度的拟合指数B随隧道长度的增大先增大后减小。隧道长度为500 m时，最大正压值的拟合指数B的值最大，约为2.613，随后，最大正压值的拟合指数B逐渐减小，隧道长度大于800 m后，最大正压值的拟合指数B约等于2.1且逐渐保持恒定。

②头车外最大负压值和最大压力峰峰值关于列车速度的拟合指数B随隧道长度的增大先减小后增大。隧道长度为300 m时，最大负压值和最大压力峰峰值的拟合指数B最小，分别约为1.411和1.484；随后，最大负压值和最大压力峰峰值的拟合指数B逐渐增大，隧道长度大于500 m后，又逐渐减小；隧道长度大于800 m后，最大正压值和最大压力峰峰值关于速度的拟合指数B约为2.1且逐渐保持稳定。

③单列车通过隧道情形下，隧道长度大于800 m时，车外最大正压值、最大负压值和最大压力峰峰值近似与列车速度的平方成正比。

(2)隧道中央等速交会情形

①头车外最大正压值、最大负压值和最大压力峰峰值关于列车速度的拟合指数B随隧道长度增大而减小，隧道长度为 1 200 m时，头车外最大正负压值和最大压力峰峰值的指数B最小，分别为1.1、1.423和1.505，之后指数B逐渐增大。

②由于列车在隧道中央等速交会时，隧道内压力环境较为复杂，车外最大正压值、最大负压值和最大压力峰峰值的取值不仅取决于列车速度，更取决于两列车进入隧道产生的压力波的叠加时刻和叠加形式，故在隧道长度范围为250～1 700 m时，车外最大正压值、最大负压值和最大压力峰峰值关于列车速度的拟合指数B波动范围较大，且无明显迹象收敛于某一数值。

3 结论

本文采用一维可压缩非定常不等熵流动模型，研究了400 km/h等级下，列车编组长度和列车速度对车体压力载荷的影响特征，得出以下主要结论：

(1)列车进入隧道和驶出隧道都将产生压缩波和膨胀波，压力波在隧道内以近似当地声速的速度传播并反射，形成了隧道内复杂的压力环境，引起了车外压力的变化。两列车在隧道内交会时，受列车高速交会的影响，车外的压力变化更加复杂。

(2)单列车通过隧道和隧道中央等速交会情形下，16节编组列车头车的外最大负压值略小于8节编组，其他车厢的最大正压值、最大负压值和最大压力峰峰值均大于8节编组动车组。车外最大正压值和最大压力峰峰值的K值由头车到尾车有逐渐减小趋势，最大负压值的K值由头车到尾车有逐渐增大的趋势。

(3)隧道中央等速交会情形下，16节编组列车的车外压力幅值和8节编组的比值K大于单列车通过情形，且最大正压值的K值较最大负压值和最大压力峰峰值要大。单列车通过隧道情形下，最大正压值的K值在1.3～2.2之间；隧道中央等速交会情形下，最大正压值的K值在1.4～3.6之间；单列车通过和隧道中央等速交会情形下，最大负压值和最大压力峰峰值的K值均小于1.4。

(4)单列车通过隧道情形下，车外压力幅值随列车速度的增大而增大，且与列车速度的B次方成正比。隧道长度为500 m时，车外最大正压值的拟合指数B最大，为2.613；隧道长度为300 m时，车外最大负压值和最大压力峰峰值的拟合指数B最小，分别为1.411和1.484；隧道长度大于800 m后，车外压力幅值随列车速度变化的拟合指数B逐渐减小并约等于2。

(5)隧道中央等速交会情形下，车外最大正压值、最大负压值和最大压力峰峰值随列车速度的增大而增大，近似与列车速度的B次方成正比，但拟合误差相对单列车通过隧道情形较大，且指数B波动范围较大(在1.1～2.75之间)，无明显迹象收敛于何值。