单向偏心受压构件配筋率、轴力、弯矩之间关系的探讨
2021-05-22王海润
王海润
河北工业大学土木与交通学院
1 引言
在混凝土结构中,我们把承受轴向压力为主的构件称为受压构件[1]。考虑到实际工程中对称配筋的应用更为广泛,本文以轴向压力作用点仅对构件正截面的一个主轴有偏心距时的单向偏心受压构件为研究对象,探讨其配筋率,所受轴力,所受弯矩之间的关系问题。
2 偏心受压构件正截面受压承载力公式计算
钢筋混凝土偏心受压构件中的纵向钢筋通常布置在截面偏心方向的两侧,随着轴向拉力N的偏心距e₀和纵向钢筋配筋率的变化,偏心受压构件可能发生大偏心受压破坏或小偏心受压破坏。
在大偏心情况下,轴力N由受压钢筋,受拉钢筋,受压区混凝土共同承担。但在实际工程中,由于存在着荷载作用位置的不确定性、混凝土质量的不均匀性及施工的偏差等因素,都可能产生附加的偏心距ea。当e₀比较小时,ea的影响比较显著。随着轴向压力偏心距的增大,ea对构件承载力的影响逐渐减小。《混凝土结构设计规范》(GB 50010—2010)规定[2],在两类偏心受压构件的正截面承载力计算中,均应计入轴向压力在偏心方向存在的附加偏心距ea。在偏心受压构件正截面承载力计算中,考虑了附加偏心距ea后,轴向压力的偏心距用ei表示,称为初始偏心距。初始偏心距可按下式计算:

式中:
e₀——所计算截面上弯矩M和轴力N的比值,即e₀=M/N。
2.1 大偏心受压构件正截面受压承载力计算公式
根据试验研究结果,对于大偏心受压破坏,纵向受压钢筋As的应力取抗拉强度设计值fy,纵向受压钢筋As’的应力取抗压强度设计值fy’。同时,偏心受压构件与受弯构件正截面受弯
承载力计算时采用的基本假定和分析方法相同。为保证计算简便并且压力的大小和作用点保持不变,构件截面受压区混凝土压应力分布取为等效矩形应力分布。其应力值为α₁fc。
根据纵向力的平衡条件及各力对受拉钢筋合力点取矩的力矩平衡条件[3],可以得出计算大偏心受压构件正截面承载力的两个基本公式:

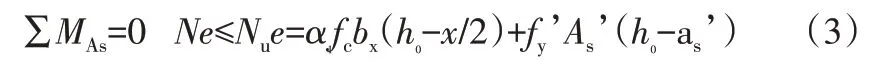
其中:

式中:
b——截面宽度;
X——等效矩形受压区高度;
h₀——截面有效高度,即受拉钢筋合力点至截面受压区边缘之间的距离。可按式(5)计算:

式中:
as,——受拉钢筋和受压钢筋至截面受拉边缘;
as’——受压边缘的距离;
e——轴向压力作用点至纵向受拉普通钢筋和受拉预应力筋的合力点的距离。
对称配筋时,As’=As,fy’=fy。将其代入上式,即可得到对称配筋情况下大偏心受压构件的正截面受压承载力计算公式:
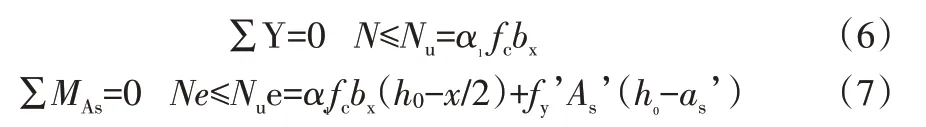
公式(6)、(7)只能在一定条件下使用,为保证构件受压时钢筋能够达到屈服强度,公式应满足:

同时,为了防止所配钢筋过多而发生超筋破坏,公式应满足:

式中:
ξb——纵向受拉钢筋屈服与受压区混凝土破坏同时发生时的相对界限受压区高度。
可按公式(10)计算[4]:

式中:
εcu——非均匀受压时的混凝土极限压应变。
其取值与所配钢筋级别和混凝土强度等级有关。
如果在计算中出现x≤2as’的情况,说明纵向受压钢筋的应力没有达到抗压强度设计值fy’,这时不能利用式(2)、(3)计算正截面承载力。可近似取x=2as’,并对受压钢筋的合理点取矩,这样可以避免出现多余未知量。计算公式即为:

式中:
e’——纵向压力作用点至受压区纵向钢筋合力点的距离。
2.2 小偏心受压构件正截面受压承载力计算公式
根据实验研究的结果,小偏心受压构件发生破坏时受压区混凝土已经被压碎,混凝土被压碎一侧钢筋可以达到受压屈服强度,故受压区钢筋应力取抗压强度设计值fy’。但是距离轴向力较远一侧的钢筋可能受拉也可能受压,且均达不到屈服强度。所以,距离轴向力较远一侧的钢筋应力表示为σs。受压区混凝土应力图形仍为等效应力图形。
σs可近似按下式计算:
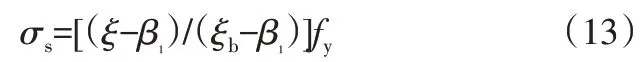
当计算出的σs为正号时,表示钢筋受拉,σs为负号时,表示钢筋受压。且按照上式计算的σs应满足:

由截面上纵向力的平衡条件、各力对距离轴向力较远一侧钢筋受力合力点取矩以及对距离轴向力较近一侧钢筋受力合力点取矩的力矩平衡条件,可以得到小偏心受压构件正截面承载力的基本公式:

将As=As’代入上式,可以得到对称配筋小偏心受压构件的计算公式,为:

将式x=ξh₀及式(13)代入式(17)和式(18)中,可以写成下列形式:
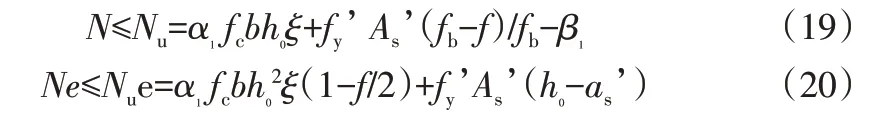
3 混凝土矩形截面单向偏心受压构件的计算曲线
将大偏心、小偏心受压构件的正截面承载力计算公式画出图像,即可较为直观的分析偏心受压构件的轴力,弯矩以及配筋率之间的关系。
3.1 大偏心受压构件的计算曲线
(1)满足2as’≤x≤ξbh₀的情况下,将式x=ξh₀,式(4)和下式:

代入式(3)中,可得:
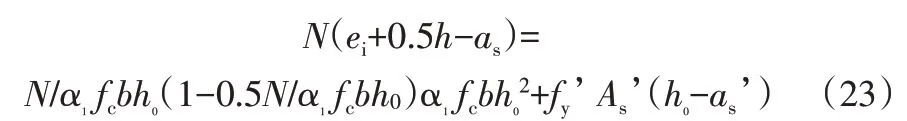
为了使曲线可以表示在不同的混凝土强度等级、钢筋级别的情况下偏心受压构件的轴力N,弯矩M,配筋率ρ之间的关系,我们把上式进行无量纲化处理,可得:
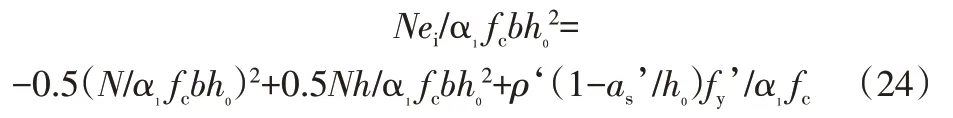
式中,ρ‘为受压一侧钢筋的配筋率。即:

令:

代入上式,得:

此时,以M’为横坐标,N’为纵坐标,即可绘制出矩形截面对称配筋情况下偏心受压构件在满足2as’≤x≤ξbh₀的情况下的计算曲线。此种情况对应计算曲线中两条水平虚线之间的曲线。
(2)在x<2as’的情况下,由对应情况的大偏心受压构件计算公式可得:
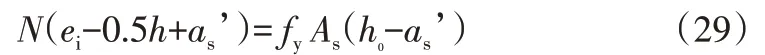
同样将上式无量纲化,即为:
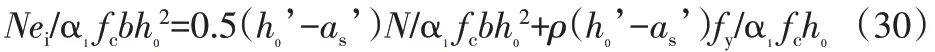
同样将式(26),式(27)代入上式,得:
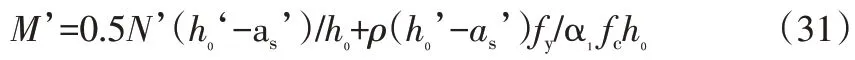
此种情况下的计算曲线对应横坐标至第一条水平虚线之间的曲线。
3.2 小偏心受压构件的计算曲线
同样将e=ei+h/2-as代入小偏心受压构件的基本计算公式中,可得:
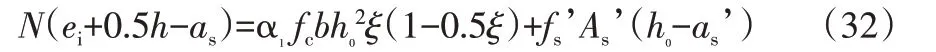
无量纲化后得:
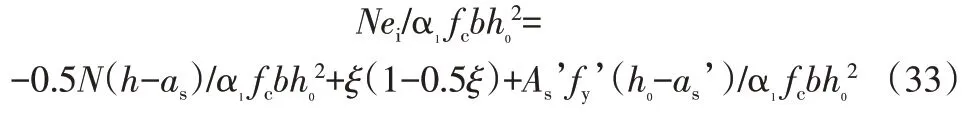
同样将式(26),式(27)代入上式,得:
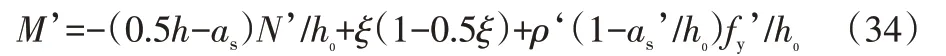
式(34)中的ξ可以由式(19)确定。将式(19)无量纲化后得:

第二条虚线以上的部分就是小偏心受压构件的计算曲线。
3矩形截面对称配筋偏心受压构件轴力N和弯矩M以及配筋率ρ之间的关系。
第二条水平虚线为界限破坏的情况。在第二条水平虚线以上,为小偏心受压破坏的情况。在第二条水平虚线以下,为大偏心受压的情况。
(1)大偏心受压构件的受弯承载力M随着轴向压力N的增大而增大,受压承载力也随着弯矩M的增大而增大。小偏心受压构件轴受弯承载力M随着轴向压力N的增大而减小,受压承载力N随着弯矩M的增大而减小。
(2)对于大偏心受压构件,当轴向力N的大小保持不变时,弯矩M越大,则所需要配置的纵向钢筋越多。当弯矩M保持不变时,轴向力N越小,则所需要配置的纵向钢筋越多。
对于小偏心受压构件,当轴向力N的大小保持不变时,弯矩M值越大则所需要的纵向钢筋越多。当弯矩M保持不变时,轴向力N越大,则所需要的纵向钢筋越多。
以上对混凝土矩形截面对称配筋单向偏心受压构件所受轴力N,弯矩M以及截面配筋率ρ之间的关系进行了较为深入的分析研究,该研究可以在实际工程中起到一定的指导作用。
