耦合干空气机制的黄土水热运移过程模拟——以山地苹果园为例*

杨 博，赵西宁，高晓东，潘岱立，霍高鹏，叶苗泰

（1.西北农林科技大学水利与建筑工程学院，陕西杨陵 712100；2.西北农林科技大学水土保持研究所，陕西杨陵 712100）

黄土高原是全球最大的黄土堆积区[1]，黄土剖面深厚，可达200 m。该区大部分属于半干旱半湿润区域，降雨量在400～600 mm 之间，光热资源丰富，是全球最大的优质苹果主产区，种植面积和产量均超过全球的25%[2-3]，但是由于干旱缺水加之果树耗水强烈，水分供需矛盾十分突出[4]。干旱缺水是制约该区农业生产与生态建设的主要瓶颈之一[5]，其中土壤水热条件是最根本因素[6-7]。因此，了解土壤水热动态过程可为该区果园生产力预报奠定基础。

数值模拟是再现土壤水热动态过程的一种可行且较为经济的方法[8-9]。与基于数据驱动的统计模型相比，基于物理过程的土壤水热耦合模型具有较强的物理意义，经得起理论推敲与试验验证，可复制性可移植性强[10-12]。目前，虽然已有研究验证了土壤水热耦合模型的可行性[13-15]，但是大部分模型假定土壤空气压强与大气压强始终保持平衡，空气自由出入地表界面，并认为土壤中只存在水相运移，忽略土壤空气流动带来的内部压力变化[16-17]。实际上，土壤水热运移是水、气两相流体在土壤孔隙中相互驱动的复杂过程，具有二相流特质，土壤干空气显著影响着土壤水分运移[9]。二相流质热传输模型STEMMUS 首次将土壤干空气方程耦合进土壤水汽热过程模拟中，综合考虑了土壤水、汽、热、气之间的耦合过程，并已得到初步应用[9，17]。黄土是一种点楞支架式多孔疏松的土壤，气相所占比例较高，总孔隙度可达30%以上[18]。该区在7—9 月份集中降雨期经常发生短时强降雨现象，极易形成超渗产流，产生有压入渗，使得土壤空气显著影响水分和热量运移过程[19-20]。但是，目前考虑土壤干空气机制的黄土土壤水热运移过程模拟较为薄弱。

本文将以黄土高原山地果园为对象，在果园土壤水热监测数据基础上，采用STEMMUS 模型模拟果园剖面土壤水热运移过程，探讨土壤干空气机制对土壤水分运移过程模拟的影响，以为黄土区土壤水分管理提供科学依据。

1 材料与方法

1.1 研究区概况

试验在陕西省子洲县清水沟村山地有机苹果种植基地（37°26′N，110°02′E）进行，海拔高度1 051 m，为典型的黄土丘陵沟壑地形。该区降水年际变化较大，年均降雨量为450 mm，多集中在7—9 月，年均气温为9.1℃，多年平均无霜期为145 d，属于温带大陆性季风气候。园区土壤主要为黄绵土，属于沙壤土，田间持水量约为22%（体积含水率），平均土壤容重为1.42 g·cm–3。

2018 年5 月在试验区果园内随机选择长势相当的3 株果树（平均种植密度为2 m×3.5 m）作为3 个重复，供试苹果树为红富士品种，树龄为10 a（至2019 年），试验观测时间为2018 年6 月1 日至2018 年9 月28 日。果树具体测定生长指标见表1。

表1 果树生长指标Table1 Apple tree growth index

1.2 观测项目及方法

土壤含水率及土壤温度：采用EC-5 型传感器（Decagon Devices Inc.，USA）测量果树根区土壤含水率与土壤温度。距树干40 cm 处预挖剖面，将传感器垂直插入土壤剖面10 cm、20 cm、40 cm、60 cm、80 cm 处。同时，将EC-5 所测土壤水分和烘干法所测体积含水量（体积含水量由质量含水量与环刀所测土壤容重相乘得到）进行拟合，校正EC-5。用RR-1008 数据记录仪（北京雨根科技有限公司，中国）自动记录传感器测量的数据，监测频率为每10 min 记录一次。模型输入采用1 小时内土壤水热数据的平均值。

气象数据：在距离果园50 m 的空旷处安置小型气象站（Decagon Devices Inc.，USA），气象数据监测项包括逐日大气温度（T）、空气湿度（RH）、降雨量（P）、太阳辐射（PAR）及距地面2 米处风速（D）。系统每30 min 记录一次数据。

果树生长指标：采用LAI-2200C 冠层分析仪（Li-Cor，USA）对果树叶面积指数（LAI）进行测量，测量间隔为7～10 d 一次。采用LI-6400XT 光合仪（Li-Cor，USA）测定果树叶片气孔导度。测定时间为白天10 点～12 点之间，此时果树气孔导度达到顶峰并保持稳定，测量间隔为1 个月。

果树根系密度分布：采用根钻法对生长期末果树根系进行实际取样，取样深度为2 m，将所取样品过40 目筛网，经人工拣根，利用扫描仪扫描根系图像（300 dpi），Delta-t scan 软件（Delta-T Devices Company，UK）分析根系图像，由图像分析结果剔除直径大于2 mm 的粗根，获取细根根长。将获得的各土层总细根根长除以对应取样土体体积得出果树各土层细根根长密度。

1.3 STEMMUS 模型

在非饱和土壤水、汽、热耦合运移理论[21-22]基础上，STEMMUS 模型充分考虑了土壤干空气对土壤水运动的影响，将土壤空气压强视为一个独立变量，耦合了土壤空气运动方程[23]，使之能够成功描述非饱和土壤水、汽、干空气和热耦合运移过程[9]，并运用隐式有限差分法，通过Matlab 软件编写程序实现对控制方程的数值求解。同时，在该模型基础上，研发人员又编入Feddes 根系吸水模型[24]及两种不同计算方法的蒸散发模块[25]，成为能模拟土壤含水率、土壤温度、植物蒸腾及土壤蒸发的SPAC模型[17]。

（1）边界条件。本研究土壤水分运动上边界选用大气边界描述，包括自然降雨与土壤蒸发。试验样地位于水平塬面上，地势平坦，地下水埋深较大。下边界条件假定为自由出流边界。热传输上边界条件采用实测土壤表层温度，热传输下边界条件采用实测底部温度。土壤空气压强梯度设为零。

（2）模型参数输入。通过环刀获取样地 0～20 cm 土样，采用CR22GⅢ型离心机（Hitachi，Japan）测定土壤水分特征曲线，并用 RETC（RETention Curve）软件拟合VG（van Genuchten）模型的土壤水分特征曲线参数。用环刀法测定土壤饱和导水率。模型率定参数是以实测参数为基础，以实现土壤水热过程模拟效果最优为目标，采用试错法对实测的土壤水分特征参数θs、θr、α、n 进行参数调优，不断优化率定期的土壤水热模拟结果，确定最优参数。土壤水力特征参数经模型率定验证后结果如表2 所示。土壤热特征参数参考Yu 等[17]测定值，取值见表2。

表2 试验地土壤水力特征参数及土壤热特征参数Table2 Soil hydraulic and thermal characteristics of the experimental orchard

为在模型中反应模拟期内苹果树叶面积指数（LAI）的连续动态变化，将冠层分析仪获取的实测数据拟合成二次函数（R2=0.79）进行线性描述，拟合结果如图1 所示。

模型中Feddes 根系吸水模型的原模型采用标准化根系密度分布函数对植物根系密度分布的描述，这种函数只适用于描述一年生作物的根系生长，而果树作为多年生植物，根系分布不规则，因此本研究采用相对深度和相对根长密度来描述果树固定根长密度分布函数b(x)[26]。

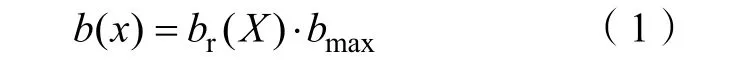
式中， br( X) 为相对根长密度； bmax最大根长密度，试验所测果树 bmax均值为0.193 3 cm·cm–3；X 为相对深度； xm为最大根系深度，设为3 m。 br( X) 采用指数函数进行拟合（R2=0.76）。

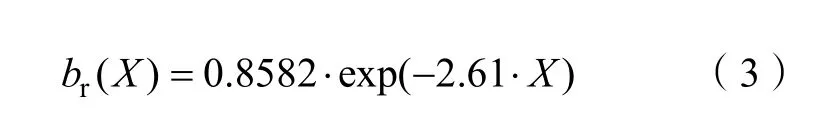
合并式（6）和式（7）得到果树根长密度分布函数：

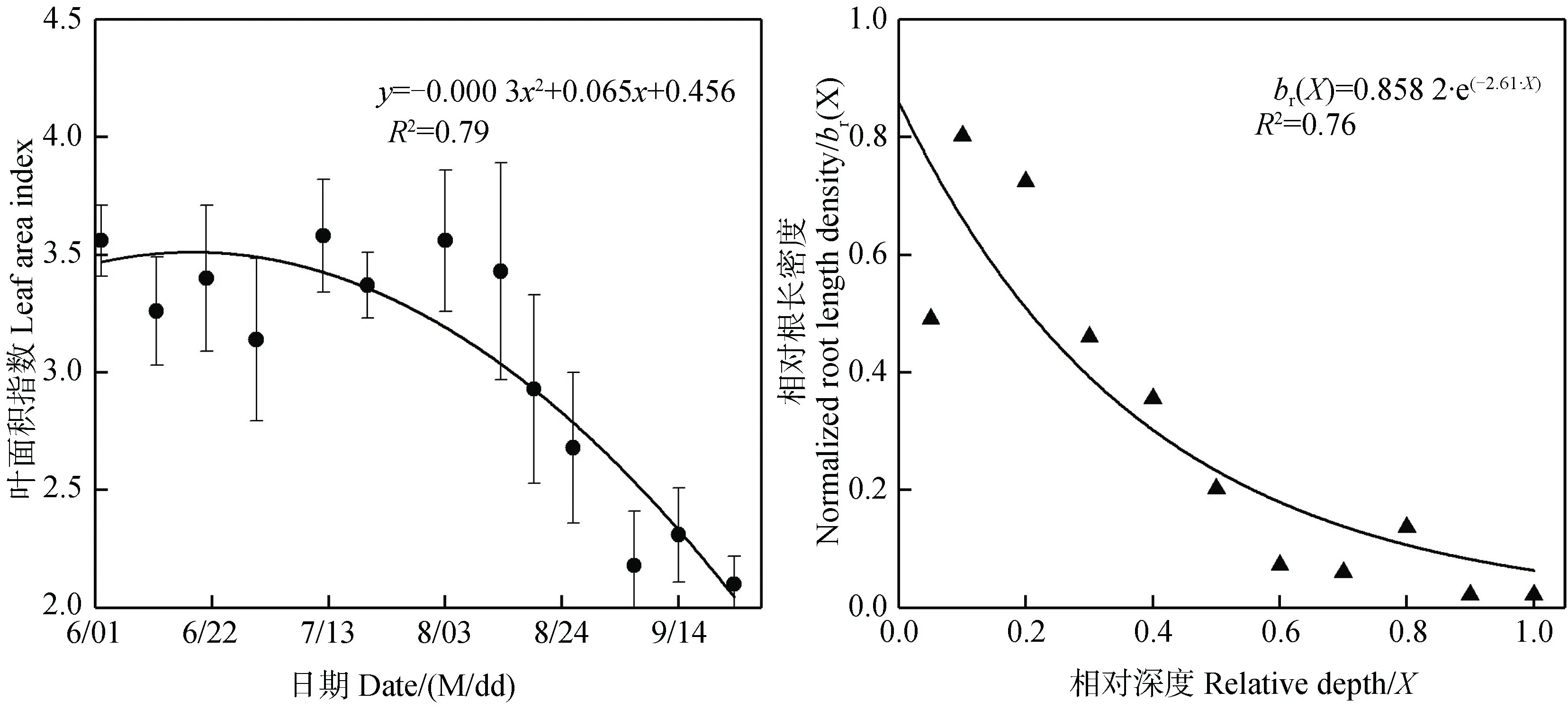
图1 模拟期内果树叶面积指数和根细密度分布Fig. 1 Leaf area index and root fine density distribution during the simulation period

（3）空间与时间离散。采用Galerkin 有限元法对控制方程进行空间离散。设定土壤剖面深度为3 m，将剖面设置38 个节点，划分37 个单元，5 个观测点，表层空间较下层空间离散性好。采用隐式后项差分法对控制方程进行时间离散。最大迭代次数为30，时间步长设为3 600 s，模拟时段为2018 年6 月1 日至2018 年9 月28 日，共2 880 h，120 d。其中，模型率定期从2018 年6 月1 日开始到2018年7 月29 日结束，模拟时间共1 416 h。验证期从2018 年7 月30 日开始到2018 年9 月28 日结束，模拟时间共1 464 h。

（4）模型验证与评价。采用归一化均方根误差（normalized root mean square error，NRMSE）、决定系数（R2）和一致性指数（agreement of index，d）评价模型土壤含水率、土壤温度模拟效果。式中，分别为iP、iO 模拟值和实测值；mO 为实测值均值；i 为次数。NRMSE 越小，表明模型模拟偏差越小；越接近1，表明模拟结果吻合度越高。

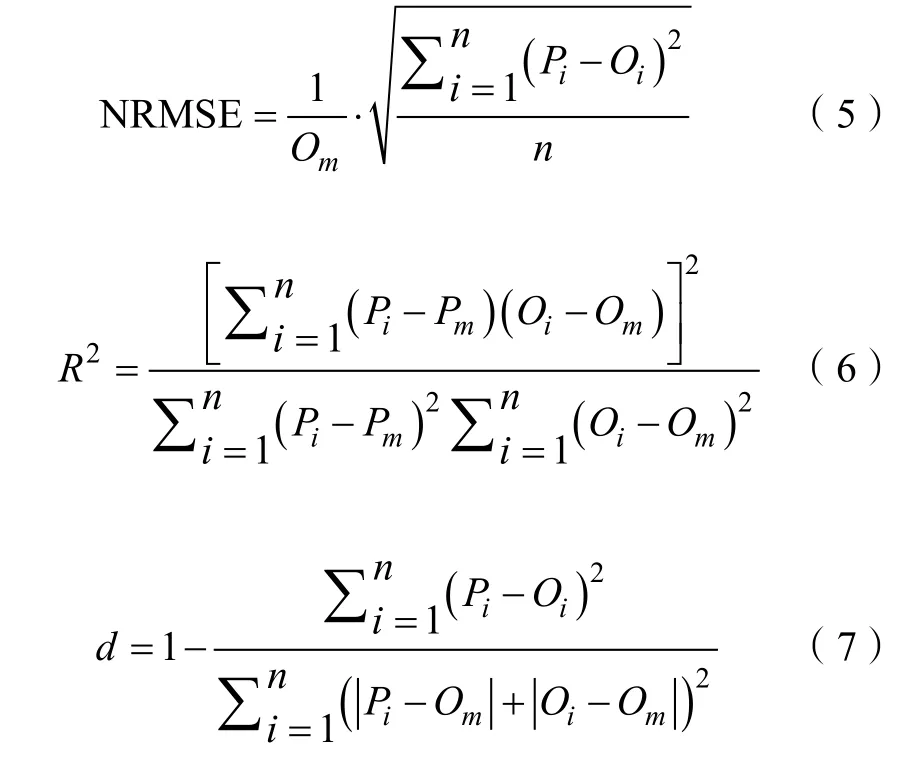
2 结 果

2.1 土壤水分的率定与验证

基于STEMMUS 模型两种蒸散计算方法，将率定期与验证期分别模拟的土壤含水率与果树根区不同土层深度观测值进行比较。由图2 和表3 可以看出，受降雨影响，模拟期内0～10 cm 浅层土壤含水率波动频繁，随着深度增加，波动幅度降低。在率定期内，ETind法模拟0～10 cm 土壤含水率与实测结果吻合程度较差，虽然在几次强降雨中，模型对降雨的响应比较敏感，能迅速模拟出水分动态变化，但模拟值较实测值存在显著高估，NRMSE 为30.0%，d 为0.81。随着土层深度的增加，模型模拟的效果变优，在土层深度为20～80 cm 时，NRMSE范围为4.7%～9.5%，d 范围为0.84～0.96。ETdir法模拟结果与ETind法模拟结果近似，除土层深度10～40 cm 内模拟结果较ETind法模拟精度低外，其余土层均优于ETind法，NRMSE 范围为10.0%～14.9%，d 均为0.88。在验证期内，两种方法模拟结果与率定期结果相近，除0～10 cm 土层模拟效果明显优于率定期外，其他土层模拟效果与率定期相差不大，均能较好地模拟土壤水分动态变化过程。

2.2 根区土壤贮水量变化

利用土壤贮水量计算方法对模型两种蒸散计算方法模拟的根区土壤贮水量动态与实测值进行对比（图3）。由图所示，率定期内ETind法模拟效果较ETdir法更接近实测值，NRMSE 为5.6%，d 为0.98。ETdir法模拟值整体较实测值偏低，土壤水分对降雨响应估计不足，NRMSE 为7.2%，d 为0.95。验证期内，ETind法模拟精度较率定期有所降低，NRMSE为5.0%，d 为0.96。ETdir法模拟精度优于ETind法，NRMSE 为5.0%，d 为0.96。与实测值相比，两种方法模拟值整体变化幅度较率定期内有所提高，但均存在土壤水分对降雨响应估计不足，以及持续干旱时期模拟值高于实测值的现象。

图2 各土层土壤含水率的模拟值与实测值Fig. 2 Simulated values and measured values of soil moisture content relative to soil layer

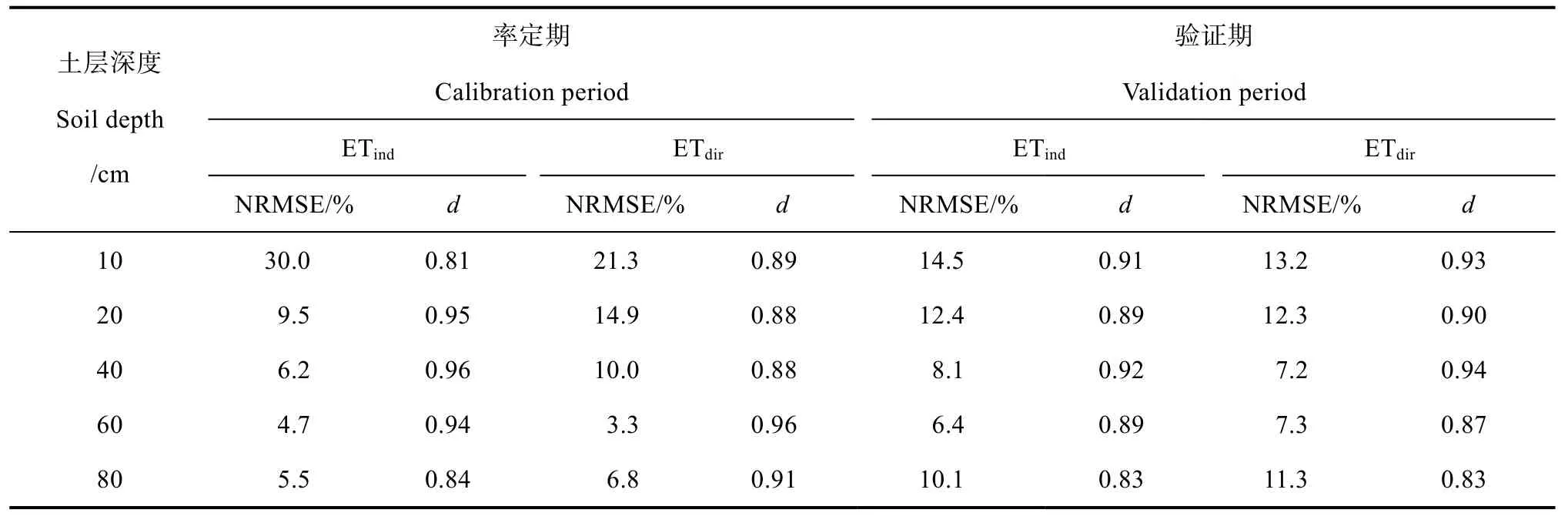
表3 土壤含水率模拟精度对比Table3 Comparison of accuracy in simulation of soil moisture content

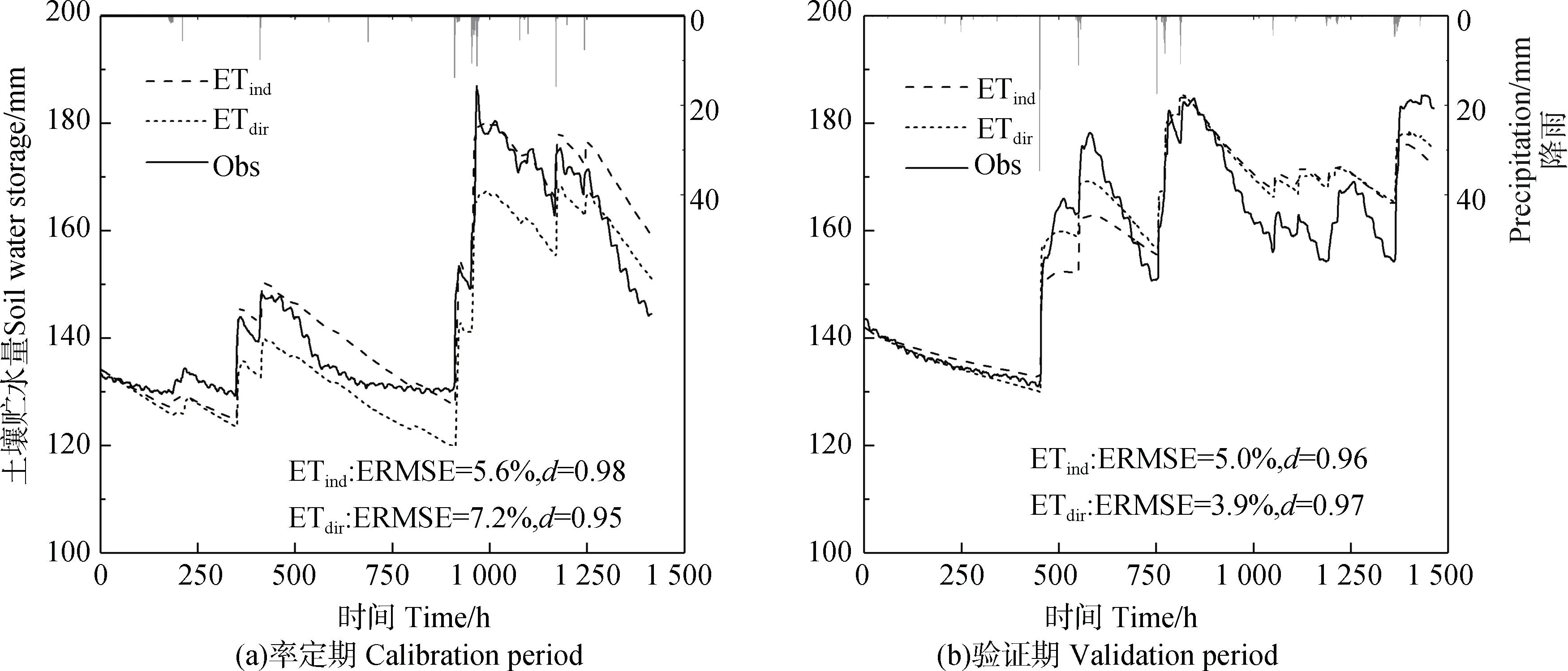
图3 土壤贮水量的模拟值与实测值Fig. 3 Simulated and measured values of soil water storage

2.3 土壤温度的率定与验证

图4 为STEMMUS 模型两种蒸腾计算方法在不同土层深度下土壤温度模拟值与实测值对比结果。结合表4 可以发现，率定期内两种方法模拟的土壤温度变化一致，但整体高于实测值，尤其在强降雨时期，模型模拟值明显存在高估现象，NRMSE 范围为 5.6%～10.0%，d 范围为 0.76～0.87。而在验证期内，两种方法模拟值与实测值较为一致，除0～10 cm 土层外，其余土层NRMSE均为0.1%，d 为0.99。

2.4 土壤干空气对土壤水分动态模拟的影响

选择模型验证期内ETdir法模拟考虑干空气机制的土壤水分动态变化（图5）。如图所示，土壤干空气对土壤水分动态模拟产生一定影响，考虑干空气影响的二相耦合模型模拟值均略低于不考虑空气影响的单相模型模拟值。尤其在降雨期间，两种模型模拟值差异较其他时段显著，且随着土层深度的增加，两种模型模拟值之间的差异逐渐减小。结合表5 可以看出，在10～20 cm 和20～40 cm 土层，耦合模型模拟精度较单相模型模拟精度略低，其余土层耦合模型模拟结果较单相模型精度更高，NRMSE 范围为4.6%～13.2%，d 范围为0.83～0.94。

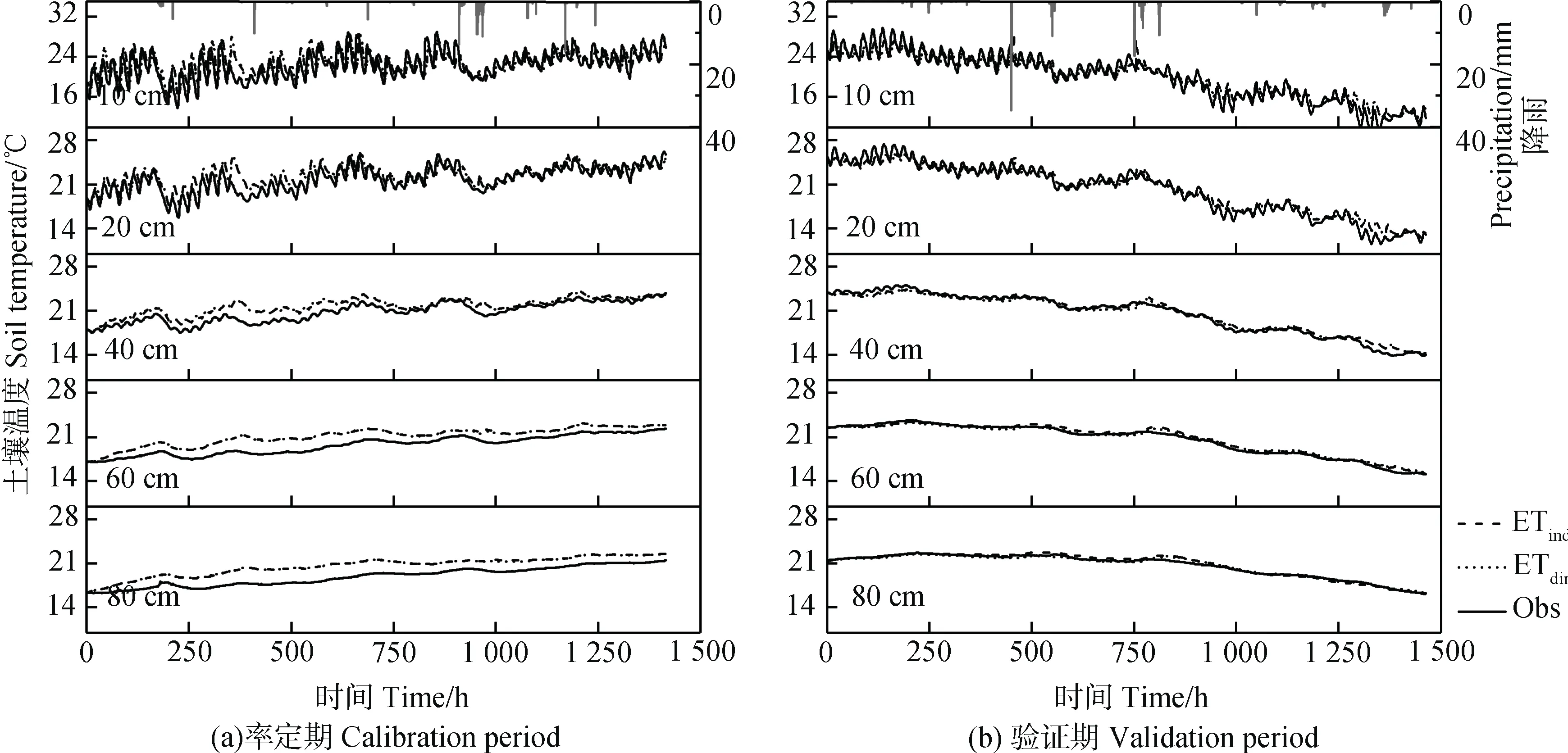
图4 各土层土壤温度的模拟值与实测值Fig. 4 Simulated and measured values of soil temperature relative to soil layer

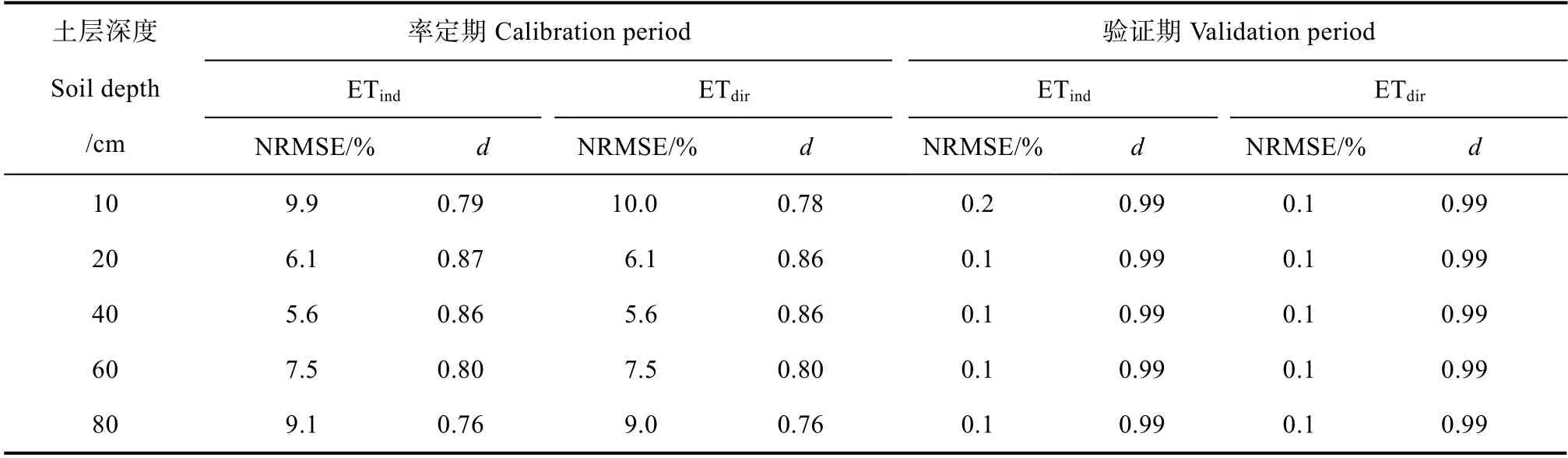
表4 土壤温度模拟精度对比Table4 Comparison of accuracy in simulation of soil temperature

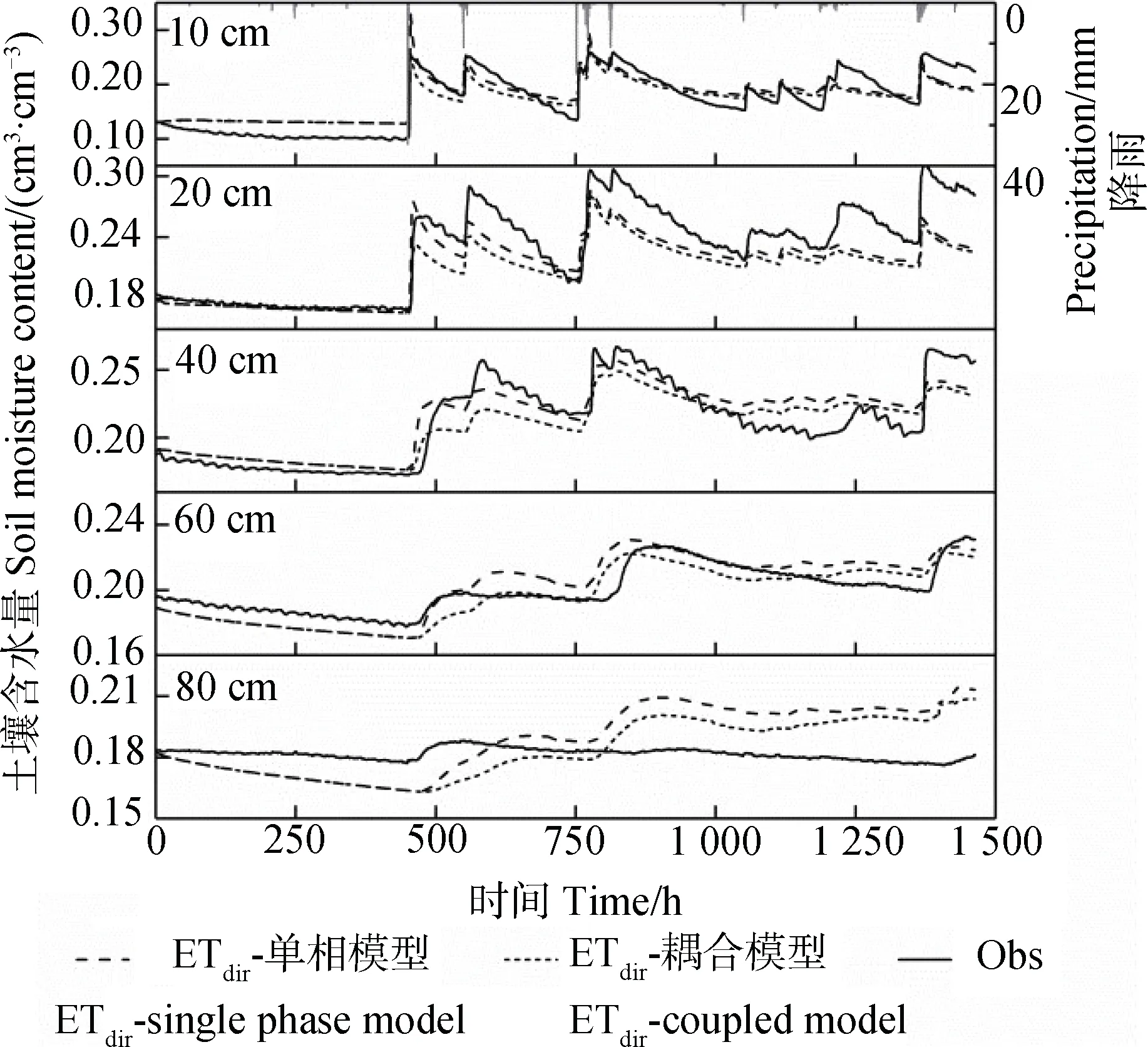
图5 考虑干空气机制的ETdir 法土壤含水率模拟值与实测值Fig. 5 Measured values of soil moisture content and values simulated with the ETdir method taking soil dry air mechanism into account

表5 考虑干空气机制的ETdir 法土壤含水率模拟精度对比Table5 Comparison of accuracy in simulation of soil moisture content between the ETdir method taking soil dry air

2.5 单次降雨土壤含水率垂直分布模拟

气机制的二相耦合模型土壤含水率模拟结果，图6b为不考虑干空气机制的单相模型土壤含水率模拟结果。选取模拟期内单日最大降雨量的雨天作为模拟对象，降雨量为55.4 mm。由此可以看出，表层土壤含水率均在降雨后1 d达到顶峰，在降雨后第2 天降低，并对下层土壤含水率进行补给。对于此次降雨，在降雨2 d 后，耦合模型显示土层深度0～70 cm内土壤含水率变化明显，说明耦合模型模拟入渗深度达70 cm，而单相模型入渗可影响到80 cm 深土壤含水率，表明单相模型模拟土壤水分入渗速率较耦合模型快。相比单相模型，耦合模型降雨后土壤含水率增加量明显较小。对于耦合模型，表层土壤含水率由降雨前1 d 的0.124 cm3·cm–3变化为降雨后1 d 的0.221 cm3·cm–3。对于单相模型，表层土壤含水率由降雨前1 d 的0.124 cm3·cm–3变化为降雨后1 d 的0.252 cm3·cm–3。表明降雨后单相模型较耦合模型模拟结果偏大，土壤入渗速率偏快。结合表6可以看出，在降雨当日与降雨后1d 内，耦合模型模拟精度高于单相模型，说明耦合模型模拟降雨入渗过程更为合理。

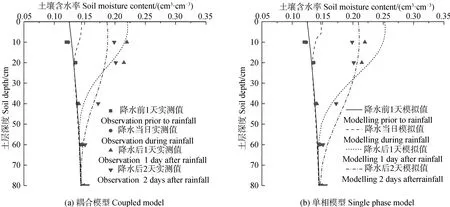
图6 单次降雨前后土壤含水率垂直分布Fig. 6 Vertical distribution of soil water content before and after each rainfall event

表6 单次降雨前后土壤含水率垂直分布模拟精度对比Table6 Comparison of accuracy in simulation of vertical distribution of soil water content before and after each rainfall

3 讨 论

3.1 土壤水分的率定与验证

STEMMUS 模型两种蒸散计算方法在率定期与验证期内模拟0～10 cm 浅层土壤含水率均较差（图2 和表3），根据野外观察，冠层截留与人为因素可能是产生这种现象的主要原因。本文试验中土壤水分传感器安置在果树冠层下方，果树冠层对降雨产生截留使渗入土壤中的降雨量较实际观测值少，而模型在输入降雨参数时未考虑到这种情况，所以导致表层土壤水分模拟结果偏高。表层土壤受除草、踩踏等人为因素影响严重，模型难以考虑到相关情况。将STEMMUS 模型率定期与验证期分别模拟的不同土层水分结果进行对比，反应出的差异各不相同，没有明显优劣趋势，产生这种情况原因之一可能是模型对土壤质地均一的假设不合适[14，27]。土壤存在空间异质性，且果树根系生长会影响传感器安装位置的土壤性质，而本文只采用20 cm 土层处土壤水力学参数作为模型单一平均的水力特征输入条件，难以符合实际情况。再者，本文根系吸水模块选取果树生长期末固定的根系分布，忽略根系动态生长过程，这对模型计算果树根系吸水会产生偏差，从而影响土壤水分模拟效果[28-29]。前人已有研究采用模型模拟黄土高原苹果园土壤水分，如李冰冰等[29]基于Hydrus-1D 模型对渭北旱塬苹果园土壤水分进行模拟，RMSE 为0.1 cm3·cm–3，决定系数R2介于0.74～0.85；童永平等[30]利用Hydrus-1D 模型模拟黄土关键带苹果园土壤水分动态变化过程，均方根误差RMSE 介于0.0149 cm3·cm–3～0.0168 cm3·cm–3，决定系数R2介于0.59～0.76。本文中STEMMUS模型模拟土壤水分动态结果经计算，RMSE 介于0.006 cm3·cm–3～0.045 cm3·cm–3，决定系数R2介于0.81～0.96，评价指标中除部分土层深度RMSE 超出上述研究范围，其余土层指标均涵盖或优于上述范围。原因是上述研究中样本量过少，且均为模拟果园深层水分变化，忽略浅层土壤水分剧烈波动对模拟结果的影响，引起评价指标RMSE 偏低。整体而言，STEMMUS 模型对模拟黄土丘陵区果园水分动态情况具有良好的适用性。

STEMMUS 模型采用两种蒸散计算方法对不同土层土壤水分进行模拟的结果不同，根据以往研究，产生这种情况是因为不同蒸散方法计算得出的蒸散量不同，从而显著影响SPAC 模型的输出结果[14，31-32]。如Anothai 等[31]发现基于CSMCERES-Maize 中FAO-56 PM 蒸散方法模拟的半干旱条件不同灌溉制度下玉米田间土壤水分效果最优；Kingston 等[32]研究发现不同潜在蒸散发计算方法会显著影响区域水资源的预测结果；吕厚荃和于贵瑞[33]根据不同气候类型的土壤水分数据对基于不同ET 计算方法的农田土壤水分模拟结果进行分析，发现Priestley-Taylor 蒸散模型模拟的土壤水分动态最优。以上研究均表明，不同蒸散计算方法对不同模型模拟土壤水分动态的影响存在差异，而本文中STEMMUS 模型两种蒸散计算方法模拟的土壤水分效果相似，均可以较好地满足模拟需要。

3.2 干空气机制对土壤水分模拟的影响

在降雨期间，STEMMUS 模型中考虑干空气机制的二相耦合模型模拟值较单相模型模拟值更接近实测值，且模拟雨水入渗速率偏小，入渗土壤水分增量偏低，影响了模拟得到的入渗深度（图5 和图6）。一般而言，模型误差主要来源于三方面：模型结构误差、输入参数误差、输入变量的测量误差。与原有模型相比，考虑干空气机制的耦合模型在结构误差会降低，但是输入参数误差和变量的测量误差仍然存在，这些误差的存在造成了模拟值与实测值之间的差异。在实际过程中，短时强降雨导致黄土表面易形成超渗产流，土壤空气被禁锢，随着水分不断入渗，土壤孔隙内空气不断积压，形成对雨水入渗的阻碍作用，使土壤含水率上升出现迟滞现象。若不考虑土壤干空气对土壤水分运移的影响，则会出现土壤含水率上升较快的现象[34]。同时，传统土壤水分运动方程中液态水与汽态水通量只考虑土壤水势、重力势与土壤温度梯度驱动力的影响[15]，而STEMMUS 模型假设土壤干空气作为一个独立状态变量存在于土壤中，使得土壤水分通量需要考虑土壤空气流动，不仅在汽态水通量中考虑水汽的扩散机制，增加了水汽的对流与弥散机制，还在液态水通量中加入土壤空气压强梯度驱动[9，17]。因此，在雨水入渗过程中土壤空气压强梯度增大，水汽的扩散、对流、弥散运移加强，从而导致土壤空气流动剧烈，形成对入渗过程的阻碍作用。所以，从研究区域实际环境与模型机理两方面不难看出，考虑土壤干空气机制模拟土壤水热动态过程是很有必要的。

4 结 论

本文采用考虑土壤水-汽-热-气耦合的STEMMUS 模型，以黄土高原山地果园为例，模拟了黄土剖面土壤水热动态过程，并用田间同步实测数据进行率定与验证，得出结论如下：（1）在率定期与验证期，模型模拟值与实测值吻合较好，STEMMUS 模型可以较好地用于模拟黄土丘陵区山地苹果园土壤水分运动、土壤温度变化情况，为果园土壤水热动态实时监测与田间水热环境管理提供了可靠的工具。（2）STEMMUS 模型中考虑干空气机制的二相耦合模型模拟值较单相模型模拟值更接近实测值，模拟雨水入渗速率偏小，主要原因是模型考虑土壤空气流动影响，考虑了土壤干空气机制，对传统水热耦合运移理论进行完善。综上，STEMMUS 模型无论在理论基础还是田间数据验证上，都表明可为黄土区田间土壤水热实时监测与管理提供技术理论支撑。