极限学习机的短期电力系统负荷预测

安徽理工大学电气与信息工程学院 周 莉 黄志祥

为了更加精确的进行电力负荷预测，本文提出了一种基于极限学习机（ELM）的电力负荷预测方法。对短期负荷中的数据样本进行分析后再将其归一化处理，构建了基于ELM的短期电力负荷预测模型。采用BP神经网络与ELM对同组电力负荷数据分别进行预测，并对两种预测模型进行对比。实验结果表明，ELM算法较于BP神经网络有着更高的预测精度，并且运行时间更短。

短期电力负荷预测是电力负荷预测的重要组成部分，准确的短期电力负荷预测可以更加经济合理的制定电力调配计划，有效的化解因电力负荷过载产生的风险，对于保障生产和生活的正常运作都具有十分重要的意义。由于电力负荷与经济、天气、节假日等因素密切相关，其变化规律具有随机性和周期性。传统方法难以捕捉电力负荷变化规律，因此预测精度较低。

针对这些方法，本文采用一种基于ELM的电力负荷预测方法，将方法与BP神经网络做对比，实验结果证明该方法可以有效的提高预测精度。

1 极限学习机(ELM)

ELM是一种新的单隐层前馈神经网络算法。极限学习机模型的网络结构与单隐层前馈神经网络（SLFN）一样，但是在训练阶段与传统的神经网络不同。相较于传统前馈神经网络训练速度慢、容易陷入局部极小值点的、学习率的选择敏感等缺点。ELM输入层与隐含层的连接权值和隐含层神经元的阈值是随机生成的，在训练过程中不需要调整。只需要设置隐藏层神经元的个数，就可以得到最优解。与传统的BP神经网络相比，ELM的优点比较明显，具有学习速度快，泛化性能好。

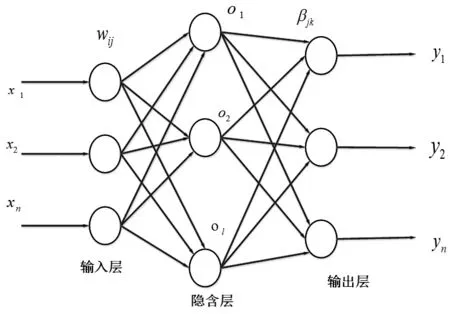
图1 单隐含层神经网络结构

对于单隐含层神经网络结构，由输入层、隐含层和输出层组成，单隐含层神经网络结构如图1所示。

其中，设隐含层神经元的阈值b；设隐含层神经元的激活函数为f(x)，输出target t和输入有如下关系：

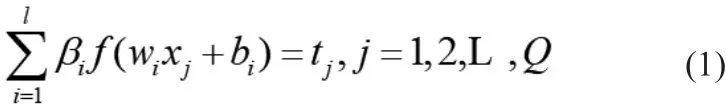
对于以上的方程组，可写成Hβ=T的形式，H矩阵有如下的形式：

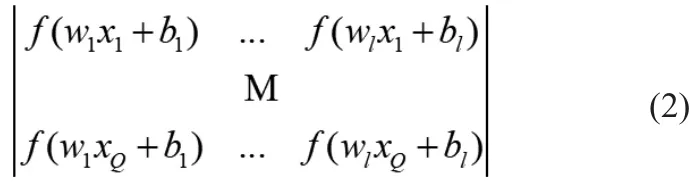
ELM在训练之前可以随机产生w，b，只需确定隐含层神经元个数及隐含层神经元的激活函数，即可计算出β，然后，这个问题被转化为一个众所周知的最小二乘凸优化问题，当然也可以对β加上Q2，Q1范数约束，这样也就变为回归预测问题。

2 实验部分

由于短期负荷曲线的周期性和连续性，在相同或相似时间段内负荷序列在变化趋势上有一定的相似性，尽管同期负载值是不同的，当外部影响因素大致相同的同时，负载变化趋势基本上是相同的，峰谷负荷出现的时间段基本是一致。针对这一特点，本文在大量的相同时间段的历史负荷数据的情况下基于极限学习机(ELM)的分析，建立负荷预测模型，即利用某一地点每15min采样的电力负荷数据建立预测模型，本文首先采用基于相同时间段从历史负荷数据中选择出与预测时间段相似的负荷数据，然后利用非线性预测性能优异的ELM训练预测，利用了良好的非线性函数逼近能力，消除了冗余信息，从而提高了预测模型的准确性和泛化能力。预测原理图如图2所示。

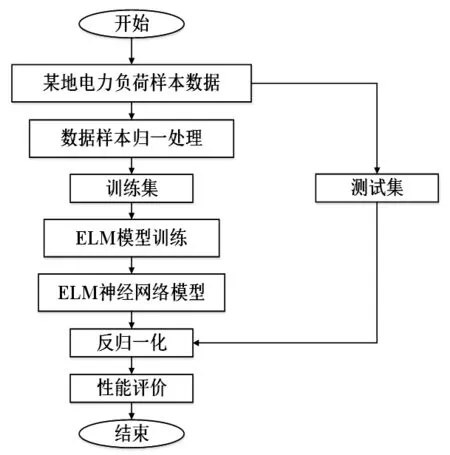
图2 预测原理图

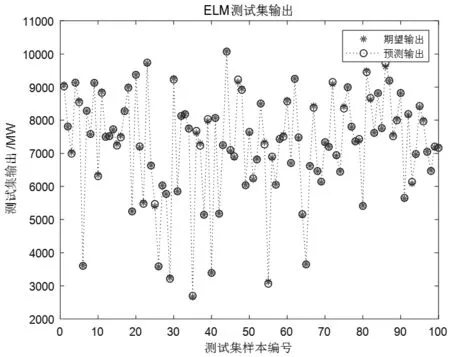
图3 测试集输出预测结果对比(ELM)

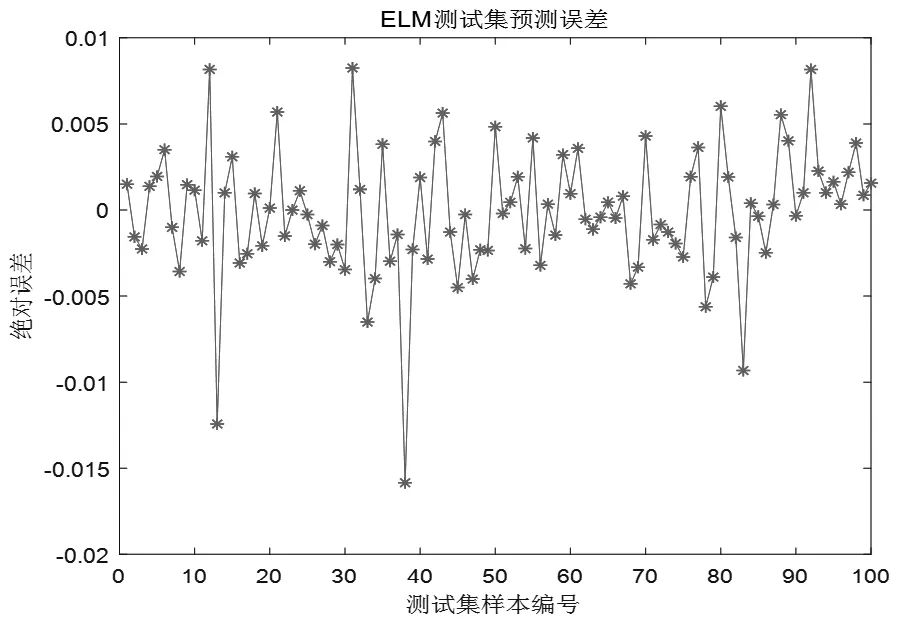
图4 测试集输出预测误差(ELM)

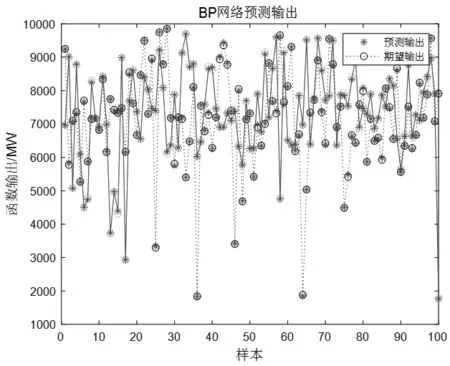
图5 BP神经网络预测输出对比

本文的仿真环境为MATLAB2018b，本文采用某地的每15min采样的电力负荷数据建立预测模型。采集产生的训练集和测试集，其中训练集1900个样本，测试集100个样本，依据预测模型的要求，创建ELM模型，通过计算均方差MSE及运行时间来评价模型优劣。并采用BP模型做对比。结果如表1所示。

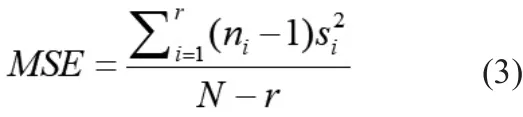
N个数据分为r组，且第i组的样本修正方差为Si2；其中分子为误差平方和，N-r为自由度。

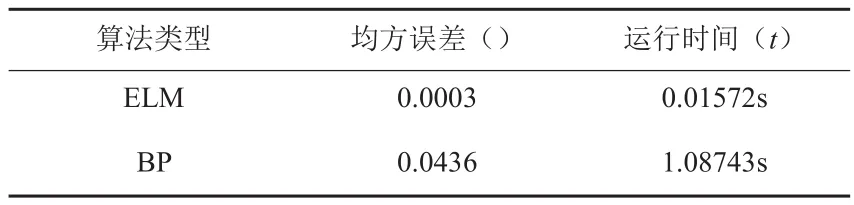
表1 均方误差和运行时间的对比

通过训练，我们建立预测模型，通过比较极限学习ELM预测模型和BP神经网络预测模型结果，ELM的均方差误差要比BP神经网络要小，且运行速度也快了很多。把历史数据样本代入ELM模型中进行电力负荷的预测，得到期望输出曲线和预测输出曲线的对比如图3所示。

并也得到测试集输出的预测误差如图4所示。

将上述的数据样本代入BP神经网络模型中，得到预测输出变化曲线和期望输出曲线对比图，如图5所示。

结论：本文采用了BP神经网络与ELM两种模型对于同一目标进行预测，结果表明：使用ELM算法构建的模型在对于电力负荷的预测上效果要好于传统的BP神经网络，ELM的学习速度更快、并且具有更好的泛化能力和更高的预测精度。ELM在电荷负荷中有很好的应用前景，为电力负荷预测提供了科学有效的方法。