洋面云液态水的星载被动微波仪器遥感反演研究进展
2021-05-21傅云飞
傅云飞
(中国科学技术大学地球和空间科学学院,合肥230026)
关键字:被动微波;洋面云液态水;辐射传输方程;反演算法
引 言
云中液态水(液态水含量LWC,Liquid Water Con⁃tent,单位:kg·m-3)或液态水路径(LWP,Liquid Water Path,单位:kg·m-2),本文统称为云液态水(Cloud Liq⁃uid Water),是云水的一部分,和云中冰水一起构成云的总水含量,它是地球水循环和地气辐射收支研究的具体参量(Stephens and Greenwald,1991),如低云(理解为水云)量的增加可抵消一部分温室效应(Ramanathan et al.,2001)。云液态水通常位于云中零度层高度以下,它可以直接转换成雨水(如暖云降水)。由于云中存在气流上升和下沉运动(特别是对流云),云液态水能到达云体上部低于零度的部位,与冰粒子进行混合(冰粒子也可下沉至零度层高度以下与水云粒子混合)。实际上,伴随着上升或下沉运动,云中零度层高度是个相对位置(不同于相对稳定高度的环境温度零度层)。因此,云液态水随高度的变化是一个非常重要的概念。从云物理学角度看,云液态水含量涉及水汽凝结成液滴过程的潜热释放,云液态水垂直分布在很大程度上可以表征云中部分潜热的分布;从数值天气预报角度看,观测和反演的云液态水数据,可以为模式云过程数值模拟提供参数化的依据或检验的标准;从人工影响天气角度看,云液态水分布关系到人工作业的位置和作业效果。
云漂浮在大气中,并在天气系统控制下随气流运动,因此云液态水直接测量方法有限,无外乎气球系仪器入云取样(Price et al.,1998;Siebert et al.,2003)、飞机入云采样(雷恒池等,2003;Vidaurre et al.,2011)、高山站仪器采样(Siebert et al.,2015;徐桂荣等,2019)或地基微波遥感反演(Westwater,1978;Hill,1991;Wei and Lu,1994;刘锦丽等,2003)或地基毫米波雷达和激光雷达探测,但上述方法均无法获得大范围的云液态水空间分布。为此20世纪学者们提出通过卫星搭载的可见光/红外仪器来遥感反演云液态水,最具有代表性的就是利用可见光通道对云滴散射敏感(即对粒子尺度敏感)、近红外通道对云滴吸收敏感(即对粒子浓度敏感)的双通道方法,实现同步反演云粒子的有效半径和光学厚度(Nakajima and King,1990),进而计算云柱垂直积分的液态水含量,被称为云液态水路径(LWP)(Arking and Childs,1985;Han et al.,1994;Naka⁃jima et al.,1995),LWP大小更取决于云光学厚度(Ste⁃phens,1984)。Fu(2014)曾就卫星双光谱反射率算法反演云参数及其应用做了综述。
与可见光/红外仪器遥感云系顶部及其附近信息相比,被动微波可以穿透云体,故能获得云体(或云柱)总液态水信息,为此利用被动微波信号反演云液态水具有一定的优点。本文对以往卫星被动微波仪器遥感云液态水的反演算法进行了梳理和归类,旨在为我国被动微波遥感反演云参数研究提供参考。文章结构如下:首先简介微波大气辐射传输方程,其次回顾被动微波通道的云液态水敏感性研究结果,然后介绍洋面被动微波反演云液态水的统计算法、物理算法、物理与统计相结合算法、多参数被动微波多通道的同步反演算法、被动微波结合可见光/红外的算法,最后探讨了未来该领域研究的发展方向。
1 微波大气辐射传输理论简介
利用被动微波仪器观测信号来反演云液态水,必然涉及到微波在大气中的辐射传输。辐射传输理论已经发展了多年,Liou(2004)对辐射传输的研究历史做了概述。大气中的辐射传输与电磁波理论密不可分,迄今可见光波辐射传输研究已有百年以上的历史。概括起来大气中的辐射传输求解主要包括离散纵标法、不变性原理、累加法。光波辐射传输大多在平面平行假定下给出其方程形式,这适合解决局域层结大气的辐射传输,因为局域大气参数和辐射强度主要在垂直方向变化。
相比可见光/红外波段,微波具有更长的波长,因此在微波谱区,只要考虑水汽和分子氧的吸收,而液滴和冰晶的粒子半径远小于微波波长,它们的吸收截面远大于其散射界面,故其散射效应可忽略。作者认为当云中存在大粒子(如强降水的大雨粒子、大冰雹粒子)情况下,微波高频波段的粒子散射效应不能忽略。在平面平行大气和非黑体表面的假定下,Liou(1980)给出了微波的辐射传输方程
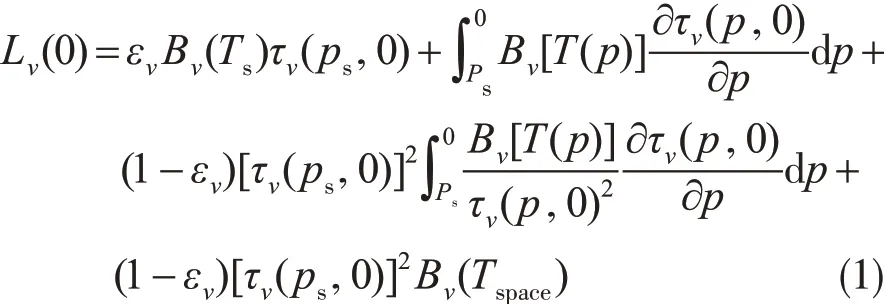
公式(1)中下标s代表地面,下标space代表宇宙背景,下标v代表频率为v的参数;ps为地面气压,卫星所处高度的气压为0。Lv(0)即表示卫星天线(p=0)接收到的频率为v的上行辐射强度,εv是地表比辐射率,Bv(T)是温度为T、频率为v的普朗克函数。τv(ps,0)是从地面(p=ps)至卫星高度(p=0)的大气透过率。
上式表明卫星天线接收的辐射强度是地表温度、地表比辐射率、宇宙背景的辐射温度、大气透过率的函数,其中大气透过率还是温度和湿度廓线的函数。故卫星天线接收到的上行辐射强度表现为四部分之和:地表上行的发射辐射强度、大气上行的发射辐射强度、大气下行的发射辐射经地表反射后的上行辐射强度、宇宙背景辐射经地表反射后的上行辐射强度。研究表明相比于高于5 GHz频率的大气发射温度,宇宙背景辐射温度非常小(Tspace≈2.7 K),所以上式最后一项通常可以忽略(Ulaby et al.,1981)。
上述辐射传输方程在特定的条件下可以简化,如Grody(1976)在前人(Stogryn,1964;Shifrin,1969)的基础上,考虑在非降水情况下局地大气处热动力平衡,因此星下点亮温TB(v)可以写成

公式(2)和(3)中T'(z)=(∂∂z)T(z),τv(z,H)为z高度至卫星高度H的频率为v的大气透过率,Ts和εs(v)分别为地表(海表)温度和频率为v的发射率(或吸收率),而1-εs(v)是地面的镜面反射率(没有考虑地表粗糙度)。在晴空情况下,低于40 GHz频率相应的av和bv小于1,因此τ10v(z,H)接近1,故晴空情况下的大气柱中除了22.235的水汽吸收外,对低于40 GHz的频率基本透明。而在云天情况下,av和bv显得重要,因为云层液态水的吸收效应显现,这就成为了反演云液态水的基础。
Grody(1976)还仔细分析了水汽和液态水在微波波段的吸收性,给出大气温度廓线和大气透过率,上式很适合频率低于40 GHz的微波通道反演水汽和云液态水。此时大气透过率由大气中的水汽、液态水和氧气决定,即τv=[τv(H2O)τv(O2)]τv(liquid)),辐射传输方程则简化为

该方程可以说是最简化、物理意义非常清晰的辐射传输方程,曾被Rosenkranz等(1978)用来反演台风的可降水量和云液态水及海面风速。
由于实际大气并非平面平行,而是一种层结大气,且云和降水粒子具有各种形状,并产生电磁辐射的偏振效应(或称为极化效应),因此发展具有偏振辐射传输理论及相应模型(如矢量辐射传输方程,Vector radiative transfer equations,VRTE)就显得十分重要。理论上求解偏振辐射传输方法需要通过高斯-塞德尔迭代方法、或蒙特卡罗方法、或倍增加法。离散纵坐标法用于计算行星大气辐射强度及通量可靠且有效,但在用于多重散射和分层发射介质中的VRTE求解时则存在问题。
为此Weng(1992a)考虑辐射场的极化特性,提出了矢量积微分辐射传输方程离散化的理论,它包括了太阳辐射和热辐射传输过程,并用多层离散纵坐标法给出了介质散射和发射的四个Stokes参数的显式解。该理论通过对多层散射粒子的散射矩阵进行平均,然后根据球面三角学对平均散射矩阵进行线性变换,得到了相位矩阵;再将向量辐射传输方程中的相位矩阵和辐射向量,展开为傅立叶余弦级数和傅立叶正弦级数形式;通过求解本征值、本征向量和特解,得到了辐射向量余弦和正弦模态离散矩阵方程组的完备解。Weng(1992b)还从多方面检验了VRTE,表明其辐射传输计算精度好。
为简洁起见,Weng和Grody(1994)给出了垂直极化和水平极化微波辐射传输方程

其中,TV和TH是垂直极化和水平极化辐射量(或理解为卫星天线接收的亮温),T为大气温度,τ是光学厚度,μ是天顶角的余弦值,ϖ是单次散射反照率,tvms和thms分别表示多次散射过程项。上式表明经过τ的μ角度垂直极化和水平极化辐射量变化,由温度为T、光学厚度为τ的气层吸收和该层内的多次散射引起的衰减造成。
如果考虑到上行和下行辐射过程,上式可改写为
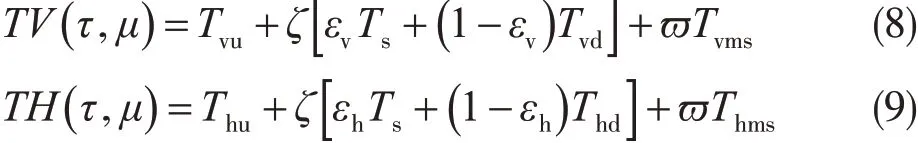
上式中εv和εh分别为垂直和水平极化的表面发射系数,在洋面它们是海表面温度SST、盐度、风速的函数;Tvu和Tvd分别为上行和下行的垂直极化辐射,Thu和Thd分别为上行和下行的水平极化辐射;ζ为大气透过率,Tvms和Thms代表多次散射项。上两式表明卫星天线接收的辐射由三项构成:大气本身的上行辐射、穿透大气的海表温度的发射辐射及大气下行辐射被海表吸收后的发射辐射、大气中的多次散射辐射。Weng和Grody(1994)基于该辐射传输方程,将大气垂直方向上分为40层,模拟计算了SSM/I各通道亮温随云液态水路径LWP的变化。
VRTE是描述实际大气辐射传输的完整形式(Weng,1992a,1992b),但它的求解具有一定的复杂性。针对微波辐射传输复杂而计算慢的不足,Liu(1998)依据平面平行大气假定,设计了一个快速且精确的微波辐射传输模式,其方程如下
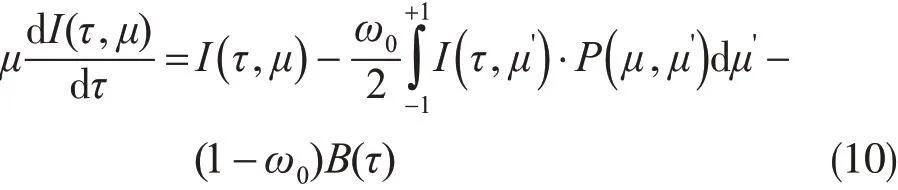
上式中I(τ,μ)是光学厚度τ处、沿μ(天顶角的余弦)方向传输的微波辐射率,它可以根据普郎克函数转换成辐射亮温;B(τ)为τ处的黑体辐射率;P为散射相函数;ω0为单次散射反照率。上式表明I(τ,μ)经过光学厚度τ的衰减变化由该厚度层内粒子散射和成分吸收引起。
Liu(1998)的研究结果表明该模式在微波观测频率为19.4 GHz和85.5 GHz、观测角为53°时,与辐射传输的精确模式(32流离散纵标法)相比,其计算速度提高了1 000倍,且最大误差不超过3 K。因此,该模式快速准确的特性在微波反演和微波资料同化方面具有优势。
总体上,微波辐射传输方程有不同的表达方式(积分式、微分式或矩阵式),但其物理意义均非常清楚,那就是经过某一介质的辐射量的变化,由介质的吸收和散射引起。考虑到地球大气的层结效应、云和降水粒子形状散射辐射的极化效应,辐射传输方程可实现不同气层间的密度(温度)和成分的吸收及发射、粒子散射及其引发的上行和下行辐射效应计算。这一过程中地面吸收(发射)和反射效应也必须考虑在内,也就涉及地表粗糙度、地面温度(海表温度、风速、盐度等)等因素。这也是辐射传输方程具有一定复杂性的原因。
2 被动微波通道对洋面参数和云液态水的敏感性
已有研究表明星载被动微波仪器观测到洋面上亮温急剧增加与洋面大量云液态水存在有关(Kreiss,1969),这是因为云液态水的发射率与水汽近似,并随着电磁波频率的升高而增大,因此被动微波仪器的频率越高,其微波亮温对云液态水也就越敏感。尽管与大气中的水汽量相比,云液态水的质量小,但由云温决定了其吸收系数大,它在地气系统中的发射辐射大(Petty,1990)。
洋面作为星载被动微波仪器遥感云液态水的辐射背景,洋面温度和风速造成的海表粗糙度将会影响仪器接收 的信号(Stogryn,1967;Chang and Wilheit,1979;Wilheit,1979a,1979b;Johnson and Cai,2002;El⁃lison et al.,2003;Irisov,2007)。Stogryn(1967)基 于Kuchhoff近似的理论,计算了微波频率为19.4 GHz亮温对洋面温度和风速变化的响应,Wilheit(1979a,1979b)提出模型将洋面描述为具有正态斜坡平面分布的集合、或各种倾斜度且各向同性平面的集合,分析了其坡度分布的方差与35 GHz或37 GHz亮温之间的关系。
由于海表发射辐射具有高度的极化性,因此利用具有极化通道的被动微波仪器(如SMMR,Scanning Multichannel Microwave Radiometer),可以较容易地获得极化通道遥感的亮温与海表风速之间的关系。研究表明随着海表风速的增大,洋面的粗糙度和泡沫均随之增加,从而导致极化通道微波亮温升高,且被动微波仪器星下点与远离星下点的观测效果还存在很大差异(Wilheit and Chang,1980)。极化通道微波亮温反演的海表温度平均偏差约为0.5 K或更小(Lipes et al.,1979;Wilheit et al.,1984;Schluessel and Luthardt,1991;Lojou et al.,1994;Wentz,1997;Wentz et al.,2000;Pulvirenti和Pierdicca,2006)。而通道之间的组合则能指示其对某些环境参数的敏感程度,如Tjemkes等(1991)指出21 GHz与19 GHz的垂直极化差对洋面发射率不敏感,而19 GHz(37 GHz)的垂直极化与水平极化差则对大气柱水汽CWV和LWP敏感。
20世纪末投入运行的TMI(TRMM Microwave Im⁃ager)因拥有对大气参数不敏感的较低频率通道(10.65 GHz),使得它成为真正意义上反演SST的被动微波仪器,在这之前的星载被动微波探测仪器频率缺少这种低频通道(Stammer et al.,2003;王雨等,2011)。王雨等(2011)利用微波辐射传输模式(Liu,1998)的模拟计算,系统地分析了TMI各通道亮温对SST、洋面风速U和CWV的响应。图1为TMI各通道的模拟亮温与洋面典型环境(SST=295 K、U=4 m·s-1、CWV=30 kg·m-2)亮温TBclr的差异(TBt-clr)随SST、U和CWV的变化。可以看到随着SST的升高,TMI垂直极化通道亮温均增加(图1a),这是因为随SST的升高,洋面发射信号增强的缘故;垂直极化通道较水平极化通道还表现了对SST更高的敏感性,且频率越低,敏感性越大,如低频10 GHz对SST变化最为敏感,当SST从283 K增加至305 K时,该通道亮温增大了12 K左右。研究表明洋面U的增大将造成洋面粗糙度增加,进而洋面发射率相应增大(Wil⁃heit and Chang,1980),故微波亮温也随之升高(图1b),但图中显示了U对水平极化通道的影响大于垂直极化通道。当CWV增加时(图1c),因其发射信号相应增大,故相应的各通道亮温也随之增加,只是水平极化通道对水汽变化的响应要高于同频率的垂直极化通道。由于85 GH频率高,故它对水汽变化更为敏感,而21 GHz通道位于22.235 GHz的水汽吸收线附近,因此该通道也表现出很高的敏感性。
王雨等(2006)还计算了TMI各通道亮温及其极化性对云液态水路径LWP变化的响应(图2),结果表明TMI任一通道亮温均随LWP的增加而增加;垂直极化通道亮温增加速率均高于水平极化通道亮温的变化速率,且通道的频率越高,其相应的亮温值越高;水平极化通道中,37 GHz水平极化通道对LWP敏感性最好。图2还表明在LWP小于0.5 kg·m-2时,85 GHz水平极化和垂直极化亮温对LWP均有很高的敏感性,即随着LWP的增加,这两个通道的亮温均增大;但LWP大于

图1 基于微波辐射传输模式模拟的洋面上TMI各通道亮温(粗线为垂直极化通道,细线为水平极化通道)随环境参数SST(a)、U(b)和CWV(c)变化与典型洋面环境参数相应亮温的差值曲线(引自王雨等,2011)Fig.1 The curves of residual error between the brightness temperatures on TMI channels(Thick and thin lines are for the vertical and horizontal polarization channel,respectively)as the function of the oceanic environmental parameters(a)SST,(b)U and(c)CWV and those under the representative condition based on simulations of microwave transfer mode(Adapted from Wang et al.,2011).

图2 当风速为8 m·s-1时辐射传输模式计算的TMI各个通道亮温与液态水路径LWP关系(引自王雨等,2006)Fig.2 Relationship between liquid water path LWP and brightness temperature at different TMI channels simulated by microwave transfer mode with 8 m·s-1 wind speed(Adapted from Wang et al.,2006).
0.5·kg m-2后,这两个通道的亮温均呈饱和趋势,且该频率的极化差减小,这是因为该频率亮温最大只能达到云顶的热辐射温度(Lin et al.,1998b);相对而言,85 GHz水平极化亮温对较低的LWP(LWP小于0.5 kg·m-2)更为敏感。因此王雨等(2006)得出结论:85 GHz水平通道亮温可用于反演云中云液态水较少时的情形。
有关利用微波辐射传输模式(特别是用矢量辐射传输模式)来模拟洋面上不同大气环境和洋面条件时,不同频率不同极化的微波亮温如何变化,仍是值得关注的问题,尤其是洋面表层参数日变化的辐射效应。洪星园等(2014)利用TMI遥感结果,研究发现热带地区存在显著SST日变化,SST日最小值多出现在早晨03∶00(当地时间,下同)至06∶00,SST日最大值多出现在午后17∶00—19∶00,SST日绝对振幅变化于1.9~3.4°C。由此不难想象SST日变化将引起星载被动微波观测背景的变化,故利用被动微波反演包括云液态水在内的云参数,必须研究洋面辐射背景的日变化规律。另一方面,洋面不同区域盐度也存在差异,它们也影响洋面的微波发射率,这方面需要细致的数值模拟研究,以减少星载被动微波仪器接收信号的背景噪音。至于海浪飞沫中粒子大小和浓度、温度及其成分(盐度等)的微波反射率,也许还需要在实验室中进行试验研究,但海浪飞沫影响星载被动微波仪器接收信号则不容置疑。
3 云液态水反演方法
被动微波反演云水含量始于20世纪60年代(Basharinov et al.,1969;Akvilonova et al.,1973),20世纪70年代中期后,利用美国的雨云5号和6号卫星搭载的NEMS(Nimbus-E Microwave Spectrometer)、ESMR(Electrically Scanned Microwave Radiometer)和SCAMS(Scanning Microwave Spectrometer)探测结果,实现了云液态水的反演(Grody,1976;Rosenkranz et al.,1978;Chang and Witheit,1979;Takeda and Natsuki,1982;Grody et al.,1980)。随后利用雨云7号卫星和海洋卫星搭载SMMR探测结果,云液态水反演算法得到了改进(Wilheit and Chang,1980;Chang and Milman,1982;Prabhakara et al.,1983;Takeda and Liu,1987)和相应的应用(Njoku and Swanson,1983;Curry et al.,1990;Lojou et al.,1991;Curry and Liu,1992)。
20世纪80年代中后期开始,美国国防部气象卫星计划(DMSP)卫星搭载的SSM/I(Special Sensor Micro⁃wave/Imager)具有七个通道(19.35 GHz、37 GHz和85.5 GHz具备水平极化和垂直极化,22.235 GHz为垂直极化),其探测结果为多种方法反演计算云液态水提供了新机遇。很多学者利用这些探测数据进行了云液态水反演算法研究,但是他们给出的反演结果却差异甚大,一方面是因为反演算法仍旧存在不足,另一方面也是缺少检验数据(Liu and Curry,1993)。随着20世纪90年代后期出现的TMI(搭载于热带测雨卫星TRMM之上)和21世纪的GMI(搭载于全球降水卫星GPM之上),则开启了被动微波遥感反演云液态水的新时代。
3.1 统计反演算法
云液态水的统计反演算法是利用统计学的计算,建立卫星仪器的被动微波亮温与地面观测的云液态水含量之间关系,来实现云液态水的反演,故也称为经验算法。该方法不需要考虑被动微波亮温与云液态水之间复杂的物理联系,仅仅利用统计计算建立两者之间的经验关系。其优点是回避了许多被动微波遥感中的不确定因素,并直观和简单易行;其缺点是使用的统计样本之间存在差异(包括样本来自区域和时间的不同),故该方法具有一定的局限性。
Alishouse等(1990)发展了一种云液态水的纯统计反演算法,即将置于洋面上的辐射计向上探测获得的云液态水视为真值,通过建立微波辐射亮温与该真值的线性回归计算,获得SSM/I反演云液态水的最佳通道和相应系数,反演算式为
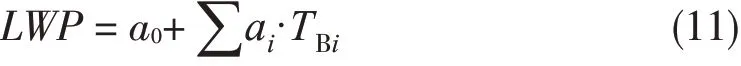
上式中LWP为云液态水路径(单位:kg·m-2),TBi为SSM/I第i个通道遥感的亮温,ai为系数,取值如表1所示。
Alishouse等(1990)的反演结果表明该算法只适合洋面的云液态水反演,因为参照洋面微波辐射计的探测结果,因此该方法在陆面和冰面的反演效果不好,其反演算式还表明SSM/I的19 V、37 H、85 V亮温信号对云液态水的反演无贡献。
类似的做法是Karstens等(1994)利用大西洋船舶上释放的无线电探空,得到真实水汽廓线,来计算绝热云液态水含量LWCad(单位:kg·m-3),并认为该含量为云液态水含量LWC的上限,且在计算云液态水含量时考虑夹卷、降水和冻结效应的影响。通过多样本的回归计算,得到LWC的反演算式如下上式中Z0为云底高度,ρ(z)为空气密度,Cp为定压空气的比热,L为汽化潜热,Γd为干绝热递减率,Γs为湿绝热递减率,LWP为云底上厚度Δh的云液态水含量。Karstens等(1994)认为上面方法得到LWC接近实际云水的垂直分布。作者认为统计回归反演算法过于简单,还会受到地域和季节的影响,因此纯统计反演算法的普适性通常有限。

表1 纯统计反演云液态水算式中的系数(引自Alishouse等,1990)Table 1 The coefficients in the purely statistical inversion of cloud liquid water formula(Adapted from Alishouse et al.,1990).
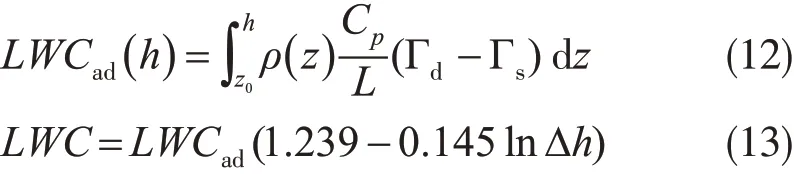
随着神经网络计算方法引入大气科学中的气候资料分析、云图识别,甚至大气温度廓线反演,神经网络计算方法也进入了LWP的反演。Jung等(1998)做了这个尝试,他们利用SSM/I观测数据对神经网络模型进行训练和测试,最终挑选了SSM/I通道的三种不同组合,指出这3种方法中,具有5个隐藏神经元的神经网络效果最好。
3.2 物理反演方法
云液态水反演的物理算法是依据微波辐射传输方程,根据所用的被动微波仪器的通道(频率),通过对辐射传输方程的合理简化,获得反演算式。Petty和Katsaros(1990)率先发展了一种基于辐射传输近似的简单物理算法,随后Greenwald等(1993)在一个可降水估算模式(Tjemkes et al.,1991)的基础上,发展了一个利用SSM/I的19.35 GHz和37 GHz,同步反演洋面(非冰面洋面)云液态水和大气柱水汽的简单物理算法,其反演算式如下
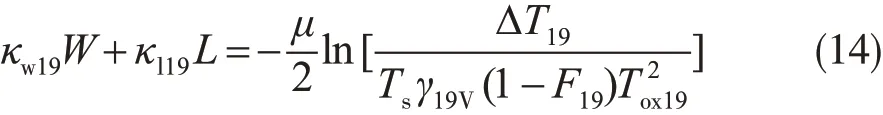

上式中L为云液态水路径(LWP)或云液态水含量垂直积分量,W为大气可降水量(PWC),μ为SSM/I入射角余弦,Ts为海面温度,ΔT19=T19h-T19v,ΔT37=T37h-T37v,κw19和κw37是19.35 GHz和37 GHz的水汽质量吸收系数,κl19和κl37是19.35 GHz和37 GHz的云液态水质量吸收系数,γ19v和γ37v为19.35 GHz和37 GHz在垂直极化方向的海面反射率。τox19和τox37为SSM/I的19.35 GHz和37 GHz的氧透过率,可通过海表温度计算(Petty,1990)
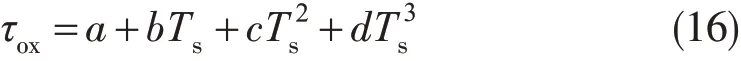
上式中a、b、c、d为系数。
F19和F37可近似为19.35 GHz和37 GHz水平极化与垂直极化的海面反射率之比,它们与这两个通道亮温及水汽等效厚度引起的海面温度衰减有关,可近似表达成
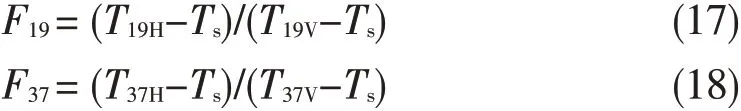
联立上面(14)、(15)、(17)、(18)四式,便可解出非降水云的L和W。该物理反演算法的出发点就是认为大气柱内的水汽和云液态水的“厚度”,造成了19.35 GHz和37 GHz的变化,在扣除洋面背景发射信号的基础上,便能通过这些变化实现L和W的反演。
对于降水云和冰云,该反演算法不适用。当W小于等于25 kg·m-2时,反演结果基本正确;但W高于25 kg·m-2时,必须考虑洋面上水汽厚度引起大气温度的递减。Greenwald等(1993)的反演结果与Petty(1990)及Hatgens(1992)反演结果的均方根差异分别为0.03和0.02 kg·m-2。进一步的研究指出更准确地物理反演云液态水,还必须考虑与洋面风速相联系的洋面发射率变化,即洋面风速变化和海表温度变化(Petty,1990)。
针对以往算法只适用于非降水情形的不足,Weng和Grody(1994)利用SSM/I极化通道探测结果,发展了一种降水云与非降水云的云液态水物理反演算法。该算法满足云系液态水的整个动态范围计算,适合低的层云和深厚的对流云的云液态水反演。首先,他们将微波辐射传输方程写成垂直极化和水平极化形式,并将洋面温度、盐度和风速效应以洋面发射率表示来简化方程;考虑到微波波长较大气中粒子尺度长,故忽略方程中的散射效应;在假定大气等温前提下,则微波衰减仅由氧气、水汽路径(WVP)和云液态水路径(LWP)吸收引起。因为氧气吸收定常不变,故利用被动微波的两个通道即可实现对WVP和LWP的反演。
Weng和Grody(1994)认为当卫星被动微波亮度变化由洋面温度、洋面发射率、水汽和云液态水路径决定时,利用SSM/I的多极化通道的探测结果,可实现WVP和LWP的反演。其反演思路与Hargens(1992)、Grody和Ferraro(1992)一致。依据垂直极化和水平极化微波辐射传输方程模拟计算,LWP算法如下
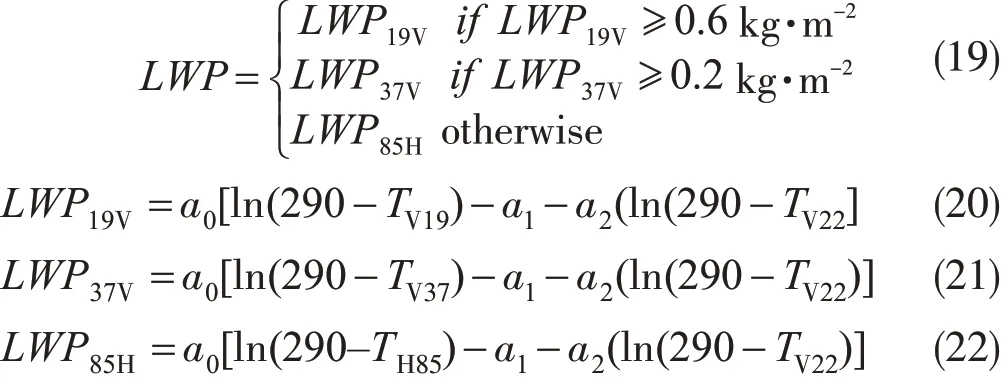
上式中的系数a0、a1、a2由辐射传输方程模拟得到。
类似于上述做法,王雨等(2006)利用热带测雨卫星的微波成像仪(TMI)观测结果,结合Liu(1998)的微波辐射传输模式模拟计算,在分析副热带地区TMI各通道的微波亮温对非降水云LWP的响应特点后,发现TMI的37.0 GHz和85.5 GHz水平极化通道探测结果对非降水云LWP响应更为敏感,并分析了TMI各单一通道反演的非降水云LWP与理论值的差异,从而建立了37.0 GHz和85.5 GHz的水平极化通道亮温联合反演非降水云LWP算式

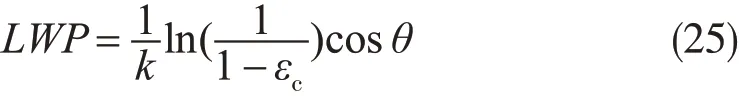
上式中k为液态水的吸收系数,是频率和云温的函数(Petty,1990);θ是微波仪器观测的入射角;εc是云的发射率,由下式计算得到

从反演原理上说,物理反演云液态水方法精度要好,因为这类方法基于微波辐射传输方程,根据使用通道和待反演参数的性质,进行合理简化,因此反演算式也简单。这一过程类似求解非线性方程,虽说解析解不易得到,但可以给出精度较高的近似解。
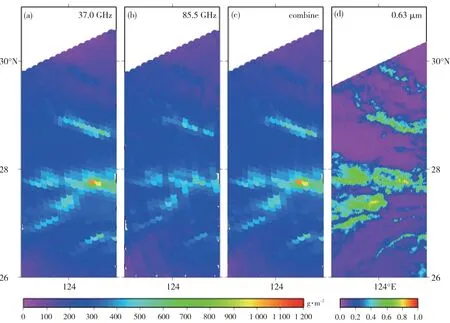
图3 基于LWP3'7H(a)、LWP85H(b)、联合反演算式(c)反演的和可见光0.63μm观测(d)的中国东部洋面非降水云的LWP(引自王雨等,2006)Fig.3 Liquid water path LWP retrieved by(a)37.0,(b)85.5 GHz horizontal polarization channel,(c)jointly at the two channels and observation by visible light 0.63μm,respectively(Adapted from Wang et al.,2006).
3.3 物理与统计相结合的反演方法
这种方法通常由辐射传输模式的模拟计算,建立计算时的输入参数(如LWP)与输出量参数(如辐射亮温)两者的关系,建立反演算式。该方法比较准确且便捷,因为它基于完备辐射理论的辐射传输模式模拟计算,可得到精确的模拟辐射信号,故与输入参数(即反演参数)之间的关系十分明确。Grody(1976)利用在NEMS的22.235 GHz和31.4 GHz通道反演洋面云液态水和水汽时,在非降水云和局域热力平衡前提下,首先对辐射传输方程进行简化,获得辐射亮温与水汽及云液态水的关系

其中TB(v)为卫星天线接收的辐射亮温,见式(2),Ts为地表温度,εs(v)是地表辐射率;W为柱水汽量,Q为柱云液态水。
然后Grody(1976)通过统计线性回归分析,获得了水汽和云液态水反演的表达式
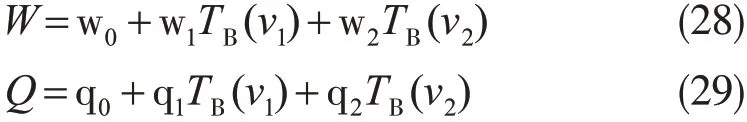
上式中TB(v1)和TB(v2)为频率v1(22.235 GHz)和v2(31.4 GHz)的辐射亮温。系数wi和qi(i=0,1,2)由统计线性回归方法分析得到(表2)。由此Grody(1976)反演了洋面上云液态水,反演水汽的标准差为0.32 g·m-2,反演云液态水的标准差为0.12 g·m-2。类似的方法还被用在SCAMS反演陆面云液态水含量和水汽含量(Liou and Duff,1979)。

表2 物理算法与统计算法相结合的反演云液态水算式中的系数(引自Grody,1976)Table 2 Coefficients in the inversion formula for cloud liquid water combined with physical algorithms and statistical algorithms(Adapted from Grody,1976).
Grody等(1980)对上述算法中W、Q与亮温呈线性关系进行了改进,利用Nimbus-6卫星搭载的SCAMS通道22.23 GHz和31.65 GHz观测亮温,并认为W和Q与这两个频率亮温呈现非线性关系
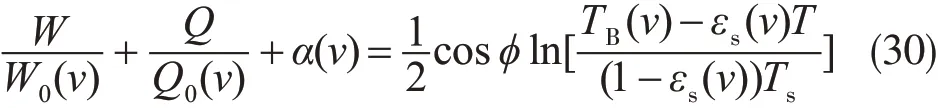
其中W0(n)、Q0(n)和α(v)分布是水汽、云液态水和氧气的吸收系数,α(v)通常因为小而可忽略,φ是局地天顶角。最后得到的W和Q反演算式如下
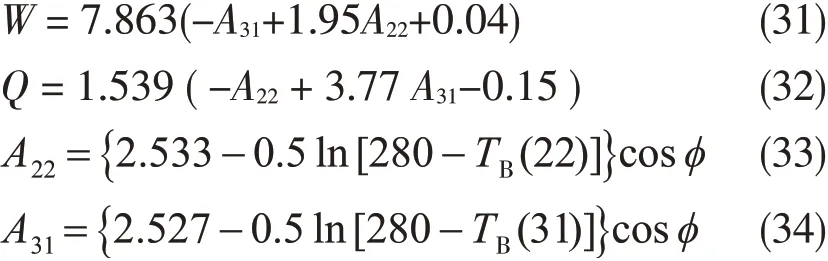
利用上述反演算法计算的W、Q与热带太平洋19个岛屿上的探空探测结果基本一致。
因为物理与统计相结合的反演方法均是基于辐射传输方程,依据研究问题所处的实际情况,进行合理的假定来简化方程,得到反演基本算式,然后对观测数据进行统计回归,得到反演算式中的相关系数,因此物理与统计相结合的反演方法具有明了的物理意义和便捷的反演算式,是一种很实用的云液态水反演算法。
3.4 被动微波多通道多参数的同步反演算法
由于卫星的被动微波天线接收到的辐射信号,既来自云液态水的辐射,还来自大气水汽、地面等的辐射,因此出现了一种利用被动微波多通道(特别是极化通道)来同步反演云液态水、降水及水汽和洋面参数的同步反演算法。前面所提到的水汽和云液态水同步反演,是这种多参数同步反演的最简单形式。Bauer和Schluessel(1993)发展了一种基于矩阵算子,并考虑多次散射和极化的辐射传输模型,研究了SSM/I各通道对多变量包括气压、温度、湿度和不同云类型在不同高度层的响应,其中云水和云冰的不均匀垂直分布用整体解析公式表示,并考虑了云和降水的覆盖率。通过他们发展的辐射传输模拟计算,借用云模式模拟计算获得诸如粒子尺度、云水、雨水的垂直结构等,还考虑了水粒子向冰粒子的转化,认为相变不改变粒子大小;并利用探空观测数据获得大气温湿垂直结构,最终建立了水汽、云液态水、云冰水和地面降水率的反演算法,并给出了反演标准差范围。
基于非线性最优估计理论,Phalippou(1996)提出了利用SSM/I观测的洋面大气湿度廓线、云液态水和洋面风速的一维变分反演方法。其具体做法是利用数值天气预报模型结果,获得高质量的先验信息,即反演参数的第一个猜测来自欧洲中期天气预报中心的预报值;然后将预报误差的协方差当作约束条件,通过辐射传输模型迭代计算获得反演截轨。
针对包括云液态水在内的多参数反演,必须使用辅助信息,如模式大气参数或其它仪器探测数据等,Wang等(2009)基于Deeter和Vivekanandan(2006)给出的辐射传输方程,推导出卫星被动微波仪器接收辐射的对数线性关系式

上式中的γi(i=0,1,…5)为TB对反演参量CWV、LWP、Tc、Ts和U的敏感因子。
Wang等(2009)指出利用TMI五个通道,便可建立五组方程,从而实现五个反演参量的反演。首先通过对TMI各通道的敏感性辐射传输计算和结果分析,选出了TMI五个对不同反演参数敏感的通道,如10 GHz、19 GHz和37 GHz水平极化通道对洋面风速、大气水汽和云温敏感,而10 GHz垂直极化通道对海温敏感、21 GHz垂直极化通道对大气水汽敏感。然后通过对(35)式求解逆矩阵转置,进而得到TMI五个通道亮温的对数线性组合方式,实现对云液态水、云温、水汽、海温、风速的反演,反演算式如下

上式中A为待反演的五个参数,TBi(i=1,2,…5)为所取的TMI不同极化通道亮温,ai(i=0,1,…5)为系数。通过在微波辐射传输方程中设定这些参数作为输入值,对上述五个通道亮温进行模拟计算,随后采取多元线性回归方法计算得到上述系数。
将所选五个通道带入(36)式,即得待反演参数的表达式,如LWP反演算式为
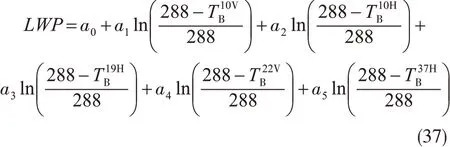
Wang等(2009)的计算表明LWP反演的均方根稳定在2 kg·m-2,偏差小于0.15 kg·m-2。图4b—f是他们利用TMI观测结果,基于式(35)反演的渤海湾非降水云云参数(云顶温度、云平均温度、云平均高度、云厚度、云水含量),其分布与可见光通道测得的云反射率(图4a)分布一致。
总之,Wang等(2009)建立了微波亮温与多参数之间存在着对数线性关系,表明了以往基于亮温线性组合方式反演算法存在缺陷。同时他们的反演算法实现了完全不依赖于辅助参数的洋面非降水云的云液态水、云温、水汽、海温、风速的同步反演方法,克服了以往多参数反演需要辅助输入参数的不足,因此Wang等(2009)的方法具有实时性,该算法正在往降水情况下发展。利用微波多通道同步反演包括云液态水在内的多参数,不用添加任何辅助资料,应该是非常好的方法。
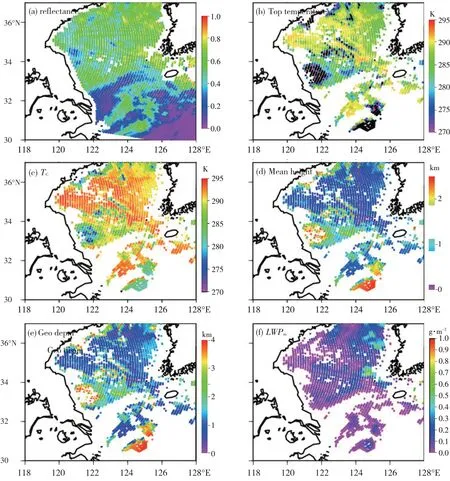
图4 VIRS可见光通道反射率分布(a)和利用TMI多通道亮温及公式(35)反演的渤海湾非降水云云参数分布(b.云顶温度;c.云平均温度TC;d.云平均高度;e.云厚度;f.液态水路径)(引自王雨,2008)Fig.4 The distributions of(a)reflectance at VIRS 0.65μm and cloud parameters(b.cloud-top temperature,c.average cloud temperature TC,d.average cloud height,e.cloud thickness,and f.liquid water path)for non-precipitation cloud in Bohai Bay based on TMI multi-channel brightness temperatures and retrieved by formula(35)(Adapted from Wang et al.,2006).
3.5 被动微波与可见光/红外相结合的反演算法
由于被动微波反演云液态水时,某些参数必须借助卫星搭载的可见光和红外仪器探测确定,这就形成了被动微波与可见光/红外相结合的反演算法。Liu和Curry(1993)在利用SSM/I反演LWP时,先将ISCCP(In⁃ternational Satellite Cloud Climatology Projec)红外信号反演的云顶温度(Tct)匹配至SSM/I的像元,借助ISCCP的热红外通道来判定SSM/I像元是晴空还是云天,冰云还是水云;考虑到降水对LWP反演的影响,采用阈值法确定SSM/I视场是否降水。最终建立了非降水云和降水云两种不同的LWP反演算法。
非降水情形为

降水情形为

上式中LWP37H、LWP19H由(25)式计算得到。
Lin等(1998a,b)通过辐射传输模式的模拟计算、结合SSM/I被动微波信号与ISCCP可见光/红外信号,给出了反演洋面非降水云LWP和云温(Tw)的查算表方法。研究中ISCCP可见光/红外信号被用来区分晴空区与云天区,并被用来反演云顶温度和云光学厚度;而SSM/I的被动微波被用来估算LWP和Tw。其辐射传输计算发现SSM/I的37 GHz水平极化通道和85 GHz垂直极化通道对LWP和Tw十分敏感,随后建立了查算表,实现了利用SSM/I的37 GHz和85 GHz亮温同时反演LWP和Tw,并分析指出气柱水汽(CWV)的不确定度是估计LWP和Tw的最重要误差来源。由于Lin等(1998a,b)论文中没有给出查算表,因此该方法不便重复。
上面所提的被动微波与可见光/红外相结合的反演算法中,可见光/红外信号主要用于云识别和云顶高度识别,LWP反演主要依赖被动微波。但研究表明对LWP小于7 mg·cm-2云,被动微波的敏感性远低于可见光波长的敏感性(Lin and Rossow,1994),因此被动微波不利于反演云液态水少的云。
LWP还可以利用云对太阳可见光的反射和对近红外的吸收进行反演。因此,LWP的光学反演方法(即短波反演的LWP,LWPshrt)与被动微波反演方法(即被动微波反演的LWP,LWPmicr)的差异及其综合引起了学者们的注意。如Greenwald等(1993)比较了SSM/I反演的LWP与非常高分辨率辐射计AVHRR(advanced very high resolution radiometer)反演的LWP差 异;Lojou等(1991)使用LWPshrt改进了LWPmicr的回归公式,从而消除了SMMR和可见和红外旋转扫描辐射计VISSR测量之间的偏差。Lin和Rossow(1994)比较发现可见光/近红外反演的LWPshrt通常大于SSM/I反演的LWPmicr,差异一般小于10%。类似的比较研究还用在AMSR-E(Ad⁃vanced Microwave Scanning Radiometer-EOS)反演的LWPmicr与MODIS(Moderate resolution Imaging Spectro⁃radiometer)反 演 的LWPshrt(Greenwald,2009;Seethala and Horváth,2010)。
Masunaga等(2002)利用TRMM搭载的可见光/红外传感器(VIRS)和微波成像仪(TMI)观测结果,提出了一种结合可见光/红外和微波传感器的物理反演算法来反演LWP。由于VIRS和TMI搭载于同一卫星平台,两者观测的时空同步性优于不同平台光学仪器与微波仪器的观测,因此可以避免诸如观测角度、太阳空间位置等差异带来的误差。由于VIRS与TMI的像元分辨率不同,VIRS约2.2 km,而TMI低频可达几十公里,故TMI视场内的云比例小,则微波方法反演的LWPmicr比较平滑,且LWPmicr比LWPshort小。为确定TMI像元的充塞度,他们利用TMI像元内VIRS像元来识别云占的比例。为减少TMI估算LWPmicr的不确定度,他们通过VIRS观测结果分析得到的云顶温度作为TMI分析的输入参数。因此VIRS与TMI的联合反演LWP吸取了光学反演和微波反演的优点,其LWPshort反演采用了Nakajima和King(1990)、Han等(1994)、Nakajima等(1995)的方法,其LWPmicr反演采用了辐射传输建立查算表。考虑到微波亮温对水汽敏感,Masunaga等(2002)在计算查算表时,与众不同的是他们考虑了大气水汽含量的垂直结构,将其作为辐射传输计算输入参量;其它洋面参数的考虑与他人的做法类似。Chen等(2007)的研究表明云粒子大小随高度的变化,对光学反演和微波反演的LWP均有影响。随着观测参数的增加,相信考虑参数越多,反演LWP的精度也越高,但反演的复杂性会大大增加。
4 展望
(1)被动微波反演洋面云液态水的研究至少有四十多年的历史,目前反演算法多,也比较成熟,并已经业务化。这主要是洋面辐射背景单一,其微波波段的发射率在
0.5左右,因此便于空中云液态水微波信号的提取。美国在此领域开展了大量的研究,这不仅是他们投入运行的卫星被动仪器多,而且他们在反演算法及相关软件方面也投入巨大。我国在此研究领域的学者占比非常少,投入也有限,这妨碍了获得卫星仪器观测结果的后期应用水平进步。相信随着认识的提高和技术的进步,中国应该能奋起直追。
(2)被动微波反演云液态水算法的未来发展方法主要在于多仪器观测结果的综合反演算法(MCA-LWP,Multisensor Comprehensive algorithm ofLWP),因为多仪器可以提供更多信息,使得反演过程不确定参量减少或被近似替代,甚至有朝一日因信息充分,使得包括云液态水在内的诸多参数能直接求解得到。因此发展同一平台被动微波、可见光/红外、云雷达观测系统,实现对云体(云顶高度、云内温度、云底高度)、大气温湿廓线、洋面温度和风速的观测,可获得云液态水等参数的高精度反演。
(3)物理算法仍是反演的基础,因此辐射传输模式(特别是矢量辐射传输模式)必须自主发展,就可在卫星仪器升空前,进行各自情况下的仿真模拟和反演算法研究,这样一旦获取卫星仪器观测数据,就可迅速进行包括云液态水在内的诸多参数反演,发布产品数据。
(4)目前,利用微波成像仪多通道进行多参数的同步反演研究还有待深入,如Wang等(2009)只给出了非降水情况下的云液态水、大气水汽、云温、海温和洋面风速的反演算式,而降水情况下的反演仍没有建立。估计降水情况下,雨粒子散射过程处理有可能更复杂。
(5)被动微波反演云液态水等参数存在一个先天性不足,就是被动微波仪器的视场分辨率粗(像元尺寸大),特别是低频通道。如何在保真的前提下,提高被动微波仪器计算分辨率,必须加紧研究。虽然目前已有一些方法,如BG理论(Backus-Gilbert theory,Backus and Gilhert.,1970)、TSVD(Truncated Singular Value De⁃composition)方法(Migliaccio and Gambardella,2005)、最小二乘法的动态曲面拟合方法(Fu et al.,2013)等,但被动微波视场内的充塞度必须知道。利用可见光/红外仪器视场分辨率高的优点,分析被动微波视场的充塞度,作为已知参数,会提高云液态水反演精度,这一方法值得推广。
(6)未来洋面液态水反演方法还必须改进在海岸附近和河口附近、高风速地区、强降水雨区的反演质量。海岸附近和河口附近的海水成分及水温会影响海水的发射率,进而影响反演精度;而高风速区海浪飞沫也会影响发射率;强降水雨区主要是云中冰粒子和雨粒子的散射效应在以往的云液态水反演中考虑不多。
(7)液态水在云中随高度的分布值得研究,可以结合星载测云雷达或地基雷达探测进行分析,或结合云模式进行数值模拟研究,由此来揭示成云至雨过程及其潜热释放规律,促进云物理学的进步。
(8)由于目前被动微波仪器观测已经积累了几十年的数据,利用这些数据反演得到长时间的云液态水数据,进行云液态水气候变化分析,可以发现气候变化带来的云水变化情况。而要建立云液态水长时间数据,必须对不同被动微波仪器的探测结果进行分析,消除它们之间探测的差异和反演算法的差异带来的误差。Elsaesser等(2017)对1998—2016年多种被动微波仪器探测结果反演的LWP进行了气候分析,相信随后更多更精细的研究会相继出现。
致谢:罗双、孙囡、孙礼璐和王梦晓四位博士生在本文撰写过程中提供输入公式及下载文献的帮助,谨致谢忱!
