基于光栅的X射线相位衬度成像图像处理系统

鲁展博 魏功祥

山东理工大学 山东 淄博 255049

一、研究背景及意义

传统的X射线CT成像是基于样品的吸收信息。如果样品中含有大原子序数元素的样品结构,如骨骼中的Ca元素,吸收信息明显,利用传统的基于吸收的CT成像可以很好的完成研究目标。但轻元素构成的组织结构器官对X射线具有相似的吸收截面,想要把病理结构从非病理结构中区分出来,用当前基于吸收衬度X射线成像的医用X射线检测系统就无能为力了。这些组织结构对X射线的吸收就非常弱了,无法利用传统的CT得到足够的衬度图像。

研究发现,在硬X射线波段,轻元素引起的相位变化是其对硬X射线吸收的103-105倍,光学元件的相移截面要远大于吸收截面。因此,要得到足够衬度的相称图像就要比振幅成像方法所需的辐射剂量小得多。利用X射线的相位信息发展的相位衬度成像,特别适合对主要由轻元素组成的物体进行低辐射剂量观测。

光波在物质中传播,由两个速度进行表征。一个是相速度,表示波节或波峰或任一相位状态的传播速度。群速度表示整个波包的传播速度。光通过物质后,电子在光波的驱动下,围绕原子核做受迫振荡运动。

通常存在三种相位信号:(1)样品像加速器或减速器,引起光波波阵面出现超前或滞后,与正相移或负相移信号对应;(2)像棱镜物体,波阵面发生倾斜,导致光的折射,折射角与相位一阶导数成正比;(3)样品像透镜,引起波阵面弯曲,导致光强的聚焦或发散,可以用相位的二阶导数描述波阵面的弯曲程度。

由此发展了三种相位检测方法:(1)利用干涉条纹探测相移;(2)利用角分辨元件探测折射角,获得相位一阶导数;(3)利用不同距离探测的光强获得相位二阶导数。

基于对软组织成像的生物医学研究要求,特别是肿瘤和癌细胞探测,需要一种能够准确提取低Z元素组成的样品结构信息的方法。由此发展了基于晶体干涉和基于传播的同轴相衬等方法。

二、原理及依据

1、莫尔条纹的光强分布。周期为d,光栅线沿y方向的光栅透过率函数T(x,y)的Fourier级数表示:

an为第n阶展开系数。光栅在距离为z的菲涅耳衍射区的衍射光场分布

在分数泰伯距离zT处:

对相位为π/2的相位光栅:在m为半整数,如1/2时,

此时,衍射光场分布表示为

2、物体相移引起的光场分布变化

其中,

为由于物体存在引起的微分相位.如果G1’和G2的光栅线的夹角为θ,则探测器所测得的莫尔条纹强度

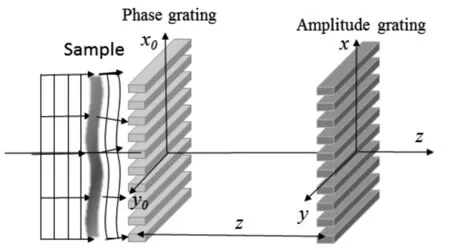
图1 光栅微分相衬成像原理图

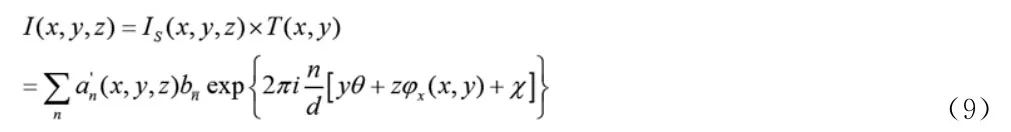
3、傅立叶变换法恢复微分相位

莫尔条纹光强分布可以简写为

其中,

对y坐一维傅里叶变换,得到其频谱分布为

4 从微分相位通过希尔伯特滤波重构相位分布的理论

4.1 从光束偏折测量中进行断层重建 从吸收或路径长度测量等通常的线积分断层重建算法是众所周知的。断层成像中最快捷和精确的算法是卷积后投影算法。该算法是重建的解析解,可以通过更精密的采样间隔来更精确的接近完备解。这里讨论如何扩展该算法到光束偏折测量中。

图2 傅立叶切片定理原理图

考虑物函数f(x,y)。通过物体z=z0平面,与x轴成θ角的普通投影可以表示为

其中x’-y’相对于x-y坐标系转过θ。省略变量z,因为它对结果的推导(derivation)没有影响。投影的一维傅里叶变换为

这里,用大写字母表示频域的函数和坐标,小写字母则表示对应的空域坐标。可以看到,物函数f(x,y)可以从一组投影的傅里叶变换中重现出来

利用卷积理论,关于Y’的傅里叶变换可以表示为

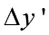
该滤波函数如图3。

图3 卷积后投影滤波函数(a)和希尔伯特频谱滤波函数(b)

卷积后投影算法可以扩展到光束偏折测量中。考虑折射率分布为

对小的倾角,可以近似的认为光束路径是直的,分别考虑两个正交的倾角。这样,(x,y)面内的高斯光束的倾角可以近似为

对于图4中的旋转坐标系

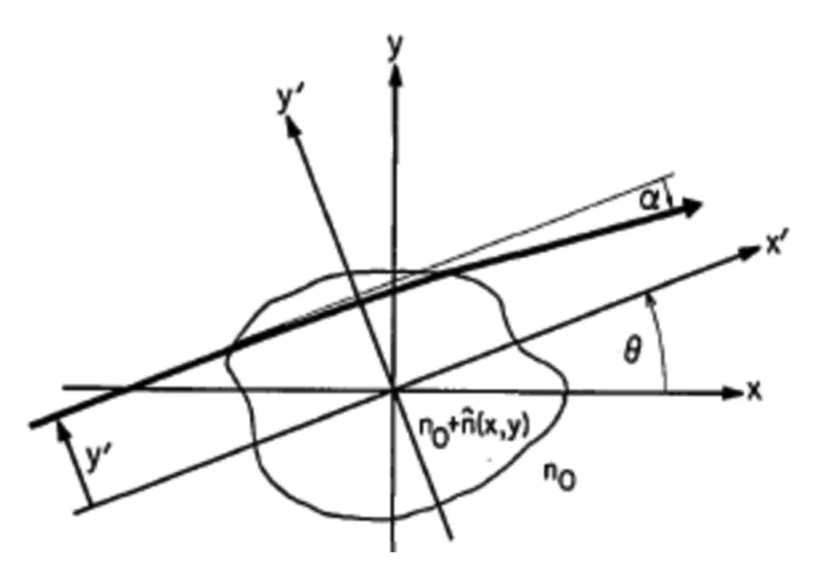
图4 傅立叶切片旋转坐标系

由公式(16)可知

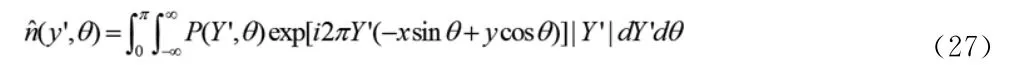
利用公式(26),(27)可得

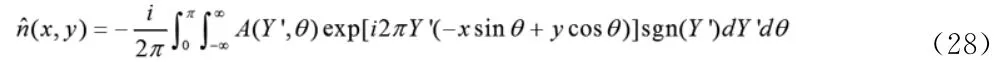
其中,sgn(Y’)是符号函数

利用逆傅里叶变换,公式(28)可以写作

在空间域中为

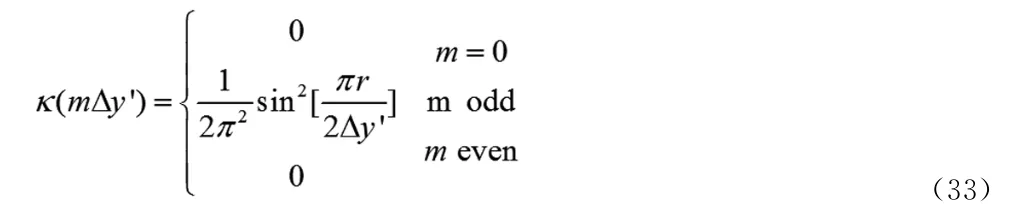
卷积后投影算法包括两部分,卷积(或投影滤波)和后投影(或对所有投影进行积分)。对投影频率成分的卷积步骤的影响是滤波函数的傅里叶变换。而对积分,后投影对连续连续无噪声数据是没有影响的。但是,对于离散投影,需要对后投影进行插值运算。对频率成分的插值是各种各样的,其影响可以通过插值滤波的选择进行消除。由于噪声的影响,后投影积分可以看作是一个平均过程,可以消除噪声。频率噪声的平均效应依赖于噪声的性质。不考虑特殊情况下的插值和后投影,对投影频率分量的卷积后投影的纯作用是由频域中滤波函数K(Y’)给出的。比较常规和横向梯度投影的滤波函数,可见对常规投影,滤波函数放大了高频分量,降低了低频分量,但对横向梯度投影的滤波作用则是平均(flat)的。因为其他对断层成像的解析形式与卷积后投影是等价的,这种滤波也适用于这些算法。这与横向梯度测量(正交方向的微分)的投影(对一个方向的积分)和原始物体(对负频成分变号)有相同的空间频率权重是一致的。

这种对横向梯度投影的不同滤波会对这种形式的测量方法产生重要的影响。一种是投影测量中包含噪声的情况。如果投影中的样品与物体中最高空间频率的间隔足够小,则在Nyquist频率附近的信号就很小。所以这些信号的空间频率成分会在低频处放大,而在接近Nyquist频率的部分接近于零。而噪声源在这种情况下通常不是限带的。如白噪声和量子噪声通常会平铺到各频率成分。对通常投影的卷积后投影重建,斜坡滤波减小了低频成分的分布,SNR通常在这里是很高的,放大了高频成分的分布,而在这些地方通常具有较小的SNR。为了减小高频噪声,可以选择不同的窗函数,来降低对传统的投影滤波函数的高频响应。降低噪声是以减小空间分辨率为代价的。对于横向梯度投影的平场滤波,低频成分的权重和高频成分的权重是相同的。低频成分对传统的投影更有意义,高频成分没有增加。我们所有的从光束偏折投影的重建都没有使用降低高频分量的窗函数,因此噪声一直是比较小的。对横向梯度投影的频域窗函数的简单形式也是有用的。因为窗函数只对负频分量产生π相移,对傅里叶重建技术活重建分析技术实现滤波相对也会简单。

三、主要功能和实用情况

基于光栅的X射线相位衬度成像图像处理系统包括四部分项目设计内容:

(1)光栅Talbot-Lau干涉仪原理展示;(2)动态光栅微分相位成像;(3)基于傅里叶变换的光栅相位CT成像;(4)扫描光栅相位CT成像。每部分都是一个独立的GUI,可以通过按钮控制项目内容的切换,并完成相应的项目内容。

1、光栅Talbot-Lau干涉仪原理展示

光栅微分相位衬度成像是利用光栅的自成像效应,又称为泰伯(Talbot)效应。该系统设计目标是针对同步辐射光源条件下的实验结果处理,所以在设计中主要针对上海光源X射线光栅相位成像系统。实验仪器包括同步辐射光源、相位光栅和吸收光栅两个光栅元件,样品台和X射线CCD组成。作为原理演示,其设计功能目标:

(1)通过光栅衍射的模拟,了解吸收光栅和相位光栅的衍射性质,特别是相位光栅的分数泰伯效应。由此了解光栅相衬成像的基本原理。

(2)计算不同光栅参数下的实验条件。如根据不同的实际光栅参数,计算分数泰伯距离,为实验提供参考。特别是在确定的光栅条件下,确定调整过程中需要用到的光栅距离等参数。

设计功能包括:

(1)根据参数,构画光栅图像。

A、光栅参数设置。包括设计光栅幅面大小参数设置,光栅周期参数,相位光栅和吸收光栅的选择,相位光栅相位值的设置。能够画出吸收光栅和相位光栅。可以设置相位光栅的相位值。

B、构画光栅二维构图和三维构图,选择不同的着色模式和三维构图的不同视角模式。

(2)观察光栅频谱结构。

(3)演示光栅在不同距离处的菲涅耳衍射图样。动态控制衍射距离,实时显示衍射光场分布。可以实时构画不同距离处的衍射光场的振幅、相位、实部和虚部等不同着色模式下的光场分布。演示光栅菲涅耳衍射的剖面结构;

(4)演示在上海光源利用光栅相衬成像实验装置所测量的部分莫尔条纹图样。

2、动态光栅微分相位成像实验数据处理系统

该部分的设计功能主要进行动态样品的微分相位成像数据处理。该方法是基于光栅莫尔条纹,利用傅里叶变换算法实现样品微分相位信息的提取。直接对样品的微分相位进行成像。

本算法的难点在于利用光栅莫尔条纹对样品相位信息的调制,怎样通过适当的傅里叶变换算法,快速提取光栅调制的微分相位信息。要求能够处理CCD的暗电流噪声,光源的背景噪声,光栅噪声等系统噪声,并能够准确地提取样品的微分相位频谱,最大限度地复原样品的微分相位信息。

项目组成目标:读入光栅微分相位成像数据,自动进行系统噪声处理。

功能目标包括:

(1)输入基本实验参数,并自动形成保存文档;

(2)选择实验数据保存路径,自动读入实验数据;

(3)实验数据自动处理,并实时显示;(由于部分实验数据处理方法还处于保密阶段,数据处理算法不能详细公开)。

(4)自动保存实验数据,制作动画演示文稿。

3、基于傅里叶变换的光栅相位CT成像

本部分的设计功能是利用傅里叶变换算法准确地提取样品的微分相位信息,并利用该方法对样品进行CT重现。

传统的CT重构是基于傅里叶切片定理,利用采集的不同角度的样品的吸收(衰减)图像数据,进行断层切片重构。传统的处理方法是利用滤波反投影处理。但对于通过处理所得到的光栅微分相位信息进行相位信息重构,需要利用希尔伯特变换滤波反投影算法,从微分相位信息直接重构相位信息。其关键技术在于希尔伯特变换滤波。

利用光栅微分相位数据,其主要优势在于可以从一组数据中直接进行提取衰减信息,相位信息和散射信息。

本部分的项目目标是:

(1)自动进行数据的背景噪声处理,得到投影图;

(2)读取投影文件总数,以及180°投影的平场数据采集周期,自动计算实验数据,得到重建的微分相位数据组,振幅数据组和吸收信息数据组。并保存实验复振幅数据,便于后续过程计算。

(3)sino构图。根据傅立叶切片定理,由不同角度的投影数据,组合不同切片的投影数据组。利用Radon变换,得到切片数据组slice。

(4)CT重构。

A:由重建的微分相位成像的切片数据组进行希尔伯特变换,得到相位衬度CT数据组。

B:根据重建的吸收像的切片数据组进行滤波反投影,得到吸收CT数据组。

C:根据重建的散射像的切片数据组进行滤波反投影,得到散射CT数据组。

(5)根据CT数据组,进行三维构图。

4、扫描光栅相位CT成像

目前,最精确的光栅相位衬度成像算法是在一个光栅周期中得到几幅样品的莫尔条纹,利用各像素的振荡曲线,准确恢复该像素点的微分相位信息。其主要缺点是需要在一个光栅周期中进行扫描,所以CT扫描速度无法提高,CT设备也更为复杂。其优点是计算精度较高。

本部分的设计功能是循环读取光栅扫描振荡图样,从每个周期的扫描图样中提取各像素的振荡曲线,并解出该像素的微分相位数据;将解出的微分相位数据作为投影数据进行CT重构。

4、基于光栅的X射线相位衬度成像图像处理系统展示

1、成像及图像处理系统

在上海同步辐射光源搭建得光栅成像系统如图5.1所示,系统主要由样品旋转台、光栅位移台、相位光栅、吸收光栅、X射线探测器以及PC控制器这几个装置构成。其中相位光栅的规格为π/2的相位调制光栅,吸收光栅则使用的规格为栅格周期2.4μm,镀金厚度为60μm的光栅,两光栅沿横向进行扫描。

图5 上海光源光栅相称成像系统

图6展示的便是动态光栅微分相位成像实验数据处理系统首页界面,功能主要进行动态样品的微分相位成像数据处理。该方法是基于光栅莫尔条纹以及利用傅里叶变换算法实现样品微分相位信息的提取。直接对样品的微分相位进行成像。利用傅里叶变换算法准确地提取样品的微分相位信息,并利用该方法对样品进行CT重现。

图6 基于光栅的X射线微分相位衬度成像(英/中文)首页

2、光栅的Talbot效应演示

功能说明:

主要包括4个控制模块:

(1)参数设置。通过设置M,N两个参数,调整光栅尺度。Period调整光栅周期像素数,光栅都采用罗切型光栅,占空比1:1。Tilt angle调整光栅线倾斜角度。通过选择phase和absorb选择光栅类型是相位型,还是吸收型光栅。如果选择相位型光栅,可以设置光栅的相位值参数,通过下拉列表框,给出1、π/2,π和random四种相位选择值。光栅参数设置完后,可以通过按钮”2D draw”和’3D draw”进行二维和三维构图,并可以通过colormap选择调色板。如果选择复选框rotate 3D,可以对三维图像进行三维旋转。

(2)频谱分析。光栅频谱结构可以通过按钮Frequency进行计算,本算法是对光栅进行FFT进行计算的,显示采用二维振幅显示。由于频谱数值范围较大,在画图过程中采用对数归一化方式显示。为了定量的观察频谱结构,可以通过按钮”Profile”,选择观察频谱中心部分的剖面结构,通过scale调整显示的振幅范围,并通过”position shift”滑块调整显示坐标位置。如果中心频谱影响频谱细微结构的观察,可以通过”delete zero frequency”切掉零级频谱进行观察。

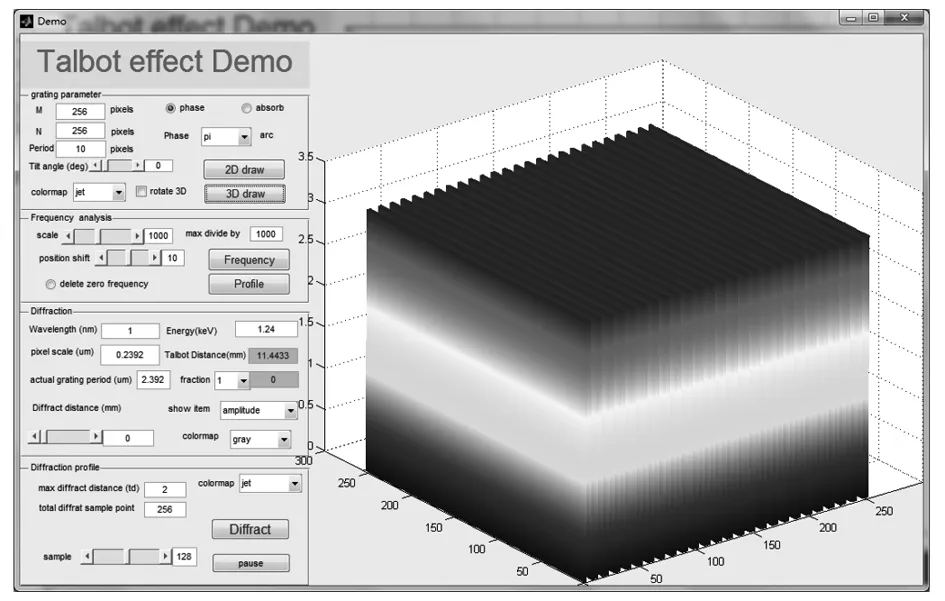
图7 光栅泰伯效应演示操作页面

(3)光栅衍射。

光栅衍射部分的主要功能:

1)根据上海光源的能量计算波长,计算公式为

λ=1.24/E

波长单位nm,Energy单位keV。

2)计算光栅模拟实验中的像素尺寸。光栅周期在功能(1)中设置,像素实际大小dx=实际光栅周期d/模拟光栅周期像素数pn。模拟光栅周期像素数为功能(1)中的period参数,实际光栅周期为“actual grating period(um)”参数,单位um。像素实际大小为”pixel scale”,单位为um。光栅一级泰伯效应距离计算公式为

Td=2d2/λ

单位一般采用mm表示。

3)在光栅相衬实验中,通常利用相位光栅的分数泰伯距离产生振幅型光栅自成像,需要观察分数泰伯距离处的光栅自成像效果。所以在本方案中增加了分数泰伯距离的计算。可以通过点选fraction选择分数值,并计算得到分数泰伯距离。

4)光栅衍射。通过拖动滑块调整不同衍射距离,本算法采用自适应标量衍射理论编写衍射函数[]。

默认显示衍射图样的振幅,可以通过选择“show item”,选择显示衍射复振幅数据的振幅、相位、实部或者虚部。

图8 光栅衍射参数设置与计算

图9中所示分数值为0时的光栅振幅像,也就是光栅本身。分数值为1的Talbot自成像。可以看到中间区域能够很好的自成像,但在边缘处会出现较大偏差,这是由于光栅边缘部分不具备周期性所致。分数值为1/2处的自成像。由于光栅占空比为1:1,在1/2Talbot距离处,也可以得到较好的光栅自成像。光栅在2倍Talbot距离处的自成像。自成像的偏差主要是由于模拟中光栅的有限大小所造成的。

图9 (a)光栅分布的振幅像(b)分数值为1的吸收型Talbot自成像(c)吸收型光栅在1/2Talbot距离处的自成像又称分数泰伯效应(d)吸收型光栅在2倍Talbot距离处的自成像

5)不同载频的莫尔条纹和实验记录结果

光栅在2倍泰伯距离处的自成像。自成像的偏差主要是由于模拟中光栅的有限大小所造成的。

(4)衍射剖面

光栅剖面部分的功能是给出光栅衍射过程中,光栅某个位置的衍射演变过程。

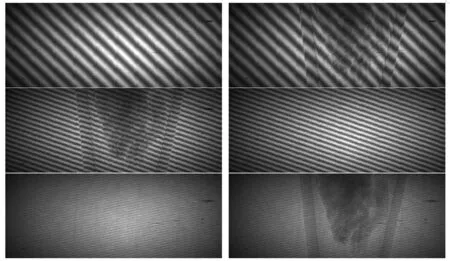
图10 不同载频的莫尔条纹和实验记录结果

3、动态光栅微分相位衬度成像处理步骤

该功能主要是进行动态样品的微分相位成像数据处理。方法是基于光栅莫尔条纹。如图12所示的便是动态光栅微分相位衬度成像处理过程整个的一个流程,主要包括暗电流噪声的矫正、背景噪声提取、物体信息提取、物体信息再现的环节。

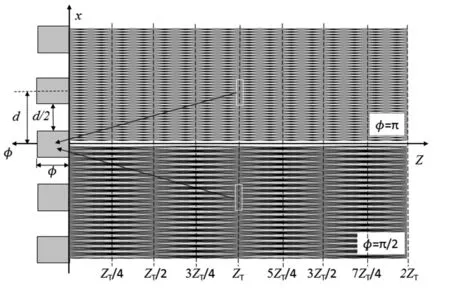
图11 相位为π和π/2的相位光栅在不同距离处的光栅衍射剖面

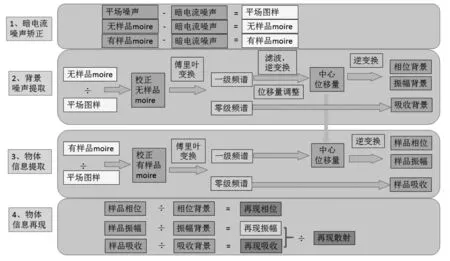
图12 动态光栅微分相位衬度成像处理流程

图13 动态光栅微分相位衬度成像的处理界面

其系统操作界面如图12所示,这里以活体蚂蚁为样本进行了动态光栅微分相位衬度成像其图像处理结果如图15,图14所示的分别为背景矫正的过程和频谱滤波截取的过程。

图14 (a)背景矫正界面示意图(b)频谱滤波截面演示示意图

图15 (a)再现相位像(b)再现振幅像(c)再现吸收像

如图16所示,可以通过按钮控制图像处理进程,实现停止,暂停,重做,退出等。并自动保存处理图像,可根据需要最后得到活体蚂蚁动态微分相位信息视频。4、基于傅里叶变换的光栅相位CT成像

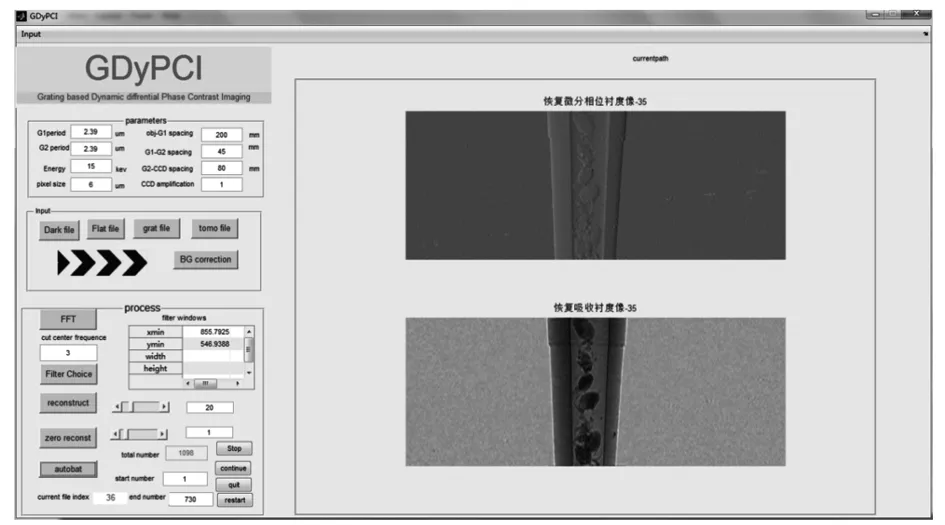
图16 自动批处理过程

(1)界面

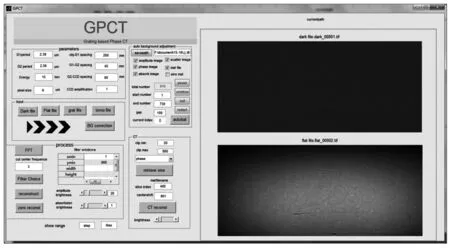
图17 光栅微分相位衬度CT成像操作界面

(2)操作与处理结果

图18 再现结果。(a)经过矫正的莫尔条纹,(b)再现吸收像,(c)再现微分相位像,(d)散射像

五、创新点和特色

1、首次实现了利用傅立叶变换方法,从一幅记录的莫尔条纹图像中恢复样品的微分相位信息。因为不需要扫描,可以实现相位的快速CT成像,有利于减小生物样品的辐照剂量。由于实验过程中,光源和光栅的非理想化,都会对实验结果引入很强的噪声信息,对相位信息的提取造成非常大的干扰。噪声来源包括暗电流噪声,平场噪声,光栅噪声。本项目的主要难点是分析这些噪声来源,并通过适当的处理步骤消除噪声干扰。

2、能够方便的选择合适的条纹载频和频谱滤波窗口。频谱滤波是一个非常敏感的操作,而莫尔条纹的频谱结构要比一般的全息图的频谱复杂很多,如何从莫尔条纹的频谱信息中获取所需要的频谱结构,是该方法的关键。滤波窗口太大,会将一些不需要的频谱结构保留下来,重叠在恢复的相位信息中,造成相位信息的不准确。滤波窗口太小,会损失样品的高频信息,使再现的样品信息不完整,甚至会出现较严重的震荡效应。

3、首次利用希尔伯特滤波反投影算法,从恢复的微分相位信息获取断层相位信息。与传统的滤波反投影算法不同,滤波反投影适用于吸收信息的再现。而我们所得到是微分相位信息,如果对每一幅微分相位图像进行相位恢复,CT重建过程会变得非常慢。因此,我们提出在滤波过程中,直接采用希尔伯特反投影算法,可以直接得到相位断层信息,处理速度明显加快。

注 释

[1]Gregory W.Faris and Robert L.Byer,Three-dimensional beam-deflection optical tomography of a supersonic jet.APPL.OPT.(1988)27(24),5202

[2]国承山等,光衍射数值模拟中不同抽样方法的适用性分析。光学学报,2008,28(3)442-446”