视为整体 巧妙解题
2021-05-20文薛丽萍
初中生世界 2021年22期
文薛丽萍
面对一些分式求值题,我们会发现用常规方法很难计算求值,但若从整体出发,触及实质,再寻求解题方法,则可化繁为简,轻松解决。
一、变形搭桥,整体换元
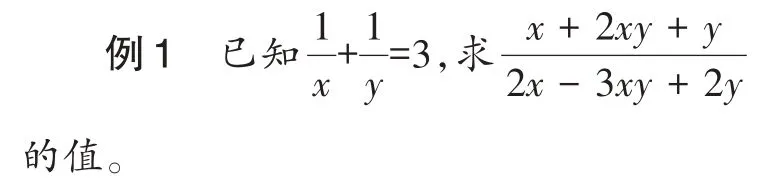
【解析】因为已知条件中有两个未知数x 和y,但只有一个关于x 和y 的方程,所以直接求出x、y 的值有一定的困难。我们不妨先来观察已知条件与所求分式之间的联系。
方法1:如果将条件变形,在等式两边同时乘xy,得到x+y=3xy,建立x+y 与xy之间的关系,将x+y 看作一个整体,整体换元,即可轻松求值。


【点评】在对一些分式进行求值时,我们可以通过变形条件或所求分式,建立两者之间的桥梁,整体代入求值。
二、借助公式,整体平方

【点评】灵活运用完全平方公式及其变形,整体平方求值,是解决此类分式求值问题的关键。
三、巧求倒数,整体颠倒

【解析】观察已知条件和所求分式,我们不难发现分子都是单项式,分母是多项式。如若将分子、分母整体颠倒,便可得原分式的倒数,再变形整理条件即可求出分式的值。


【点评】通过探寻分式分子、分母之间的内在特性,将分子、分母整体颠倒,也是我们解决复杂分式求值问题的常用方法。
同学们,我们要善于观察、挖掘问题中隐含的信息,运用整体思想简化分式求值问题,提高正确率,发展数学思维。
