一种识别EMD 虚假分量的新方法
2021-05-20范津玮刘晓波
范津玮 刘晓波
(贵州大学电气工程学院,贵州 贵阳 550000)
0 引言
EMD 方法是由美国的NASA 的Huang 等人所提出, 由于该方法具有良好的时频特性和自适应性,被许多专家学者广泛应用于各个方面。 例如,在结构分析领域应用到桥梁监测和模态响应分析,在自然科学领域应用于海洋、大气、天体等的观测和地球物理分析,在生物学领域应用于心率变换和肺部血压信号分析,在故障诊断领域应用于旋转机械信号分析[1]和电力系统暂态故障信号分析[2]。
由于EMD 分解的终止条件、 插值误差和端点效应等影响,常常会出现分解过度的现象。 这会导致分解得到的IMF 分量个数大于原有信号的组成个数,而多余的IMF 分量便是虚假分量。这些分量与原信号相关性较小,不能准确反映原信号的特征,所以需要准确识别出虚假分量。
1 E MD 方法及其虚假分量问题
1.1 EMD 方法
EMD 分解是一种新的自适应处理非平稳信号分析方法,适用于处理非线性、非平稳性的时间序列数据。 某信号使用经验模态分解(EMD)对其进行分解后可以得到不同时间尺度的IMF 分量。 EMD 的基本公式为:
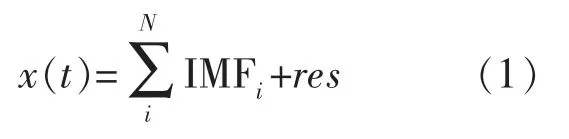
其中,x(t)为原始数据信号,IMFi为第 i 个 IMF 分量,res 为不能再分解的剩余分量。
1.2 虚假分量问题
下面以某一信号x(t)为例说明EMD 分解过程中产生的虚假分量问题。
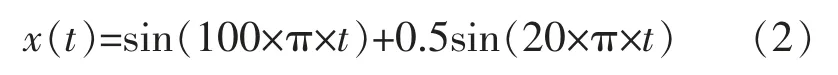
其中,采样频率 1 000 Hz,采样点数 1 000 点。 其波形图如图1 所示。对该信号进行EMD 分解,结果如图2 所示。 进一步求各阶IMF 的傅里叶频谱图,结果如图3 所示。
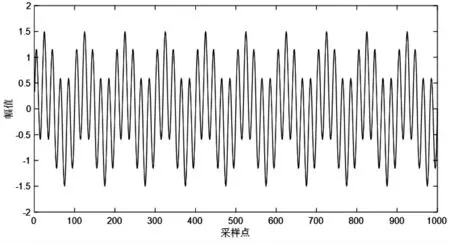
图1 仿真信号波形图

图2 EMD 的分解结果图

图3 各IMF 分量的傅里叶频谱图
从图3 可以看出, 第一个IMF 与第二个IMF 的频率成分与原始信号的两个频率成分50 Hz 和10 Hz是相符合的。第三个、第四个IMF 与剩余分量res 的频率分量在原信号中都没有出现, 故由此可推断出,除前两个IMF 外其他均为虚假分量。
目前, 虚假分量的消除方法有相关系数法、K-S检验法。 下面介绍这两种方法的优缺点。
相关系数法是通过计算各IMF 分量与原信号之间的相关系数。 若两者之间相关系数较大则判定为是有效的IMF 分量,若两者之间相关系数较小,则判定为虚假分量。 但文献[3]通过使用相关系数法对虚假分量的识别过程中发现两个问题:(1)只有第一个IMF 分量的相关系数很大,其他分量的相关系数很小;(2)通过人为设定阈值大小来界定IMF 分量是否为虚假分量,存在将真实分量误判为虚假分量的可能。
K-S 检验法的全称为Kolmogorov-Smirnov 拟合优度检验法。 该方法通过计算各IMF 分量与原信号的累积分布函数之间的差异。若某一IMF 分量与原信号直接的相似概率接近1,则认为该IMF 分量有效,若相似概率接近0,则认为该IMF 分量为虚假分量。 但文献[4]指出该方法所需方差比率较大,因此适用性较低。
2 能量比值法
本文所提的能量比值法是通过比较某一IMF 分量的能量与所有IMF 的能量之和的比值来对虚假分量进行判别。
由于终止条件和插值误差等因素的影响,会造成EMD 在分解过程中,无法完全一模一样地分解出组成原信号的各分量,这会导致在整个数据序列的某些个点上会产生一定微小误差。 从公式(2)可知第一个IMF 分量应始终为幅值1 的正弦函数,但在实际分解得到的图2 中第一个IMF 分量的某些波峰处幅值不为1,由于误差很小所以肉眼难以从图中直接看出。
由于端点效应问题的存在,故会采用一些方法去抑制端点效应,但是再好的方法也不能完全消除端点处因缺少极值点而导致的包络线拟合不符合信号内生规律带来的影响,这会使得分解出来的IMF 分量在端点处的数值产生一定的误差。 从图2 中第一和第二个IMF 分量的左右两端均可以看出,两端局部的数据点的数值与公式(2)中幅值为1 和0.5 的正弦函数数值有一定误差。
EMD 分解的终止条件、插值误差和端点效应处理方法等问题共同导致了虚假分量的产生,但这些误差要么很微小要么也只是在端点处产生。 从图2 中第三个IMF 分量可以看出虚假分量在两端的数据点上存在一定的数值且数值会小于有效分量的幅值,中间的数据点的数值均围绕在0 左右。 所以虚假分量的能量比起有效分量的能量小得多, 数量级至少相差二,对比明显,不会造成误判。
能量是信号的特征常量,假设有限长信号序列x(t),信号的能量特征可以用能量密度来表示它表示在t 时刻每单位时间内信号的能量强度。 信号总能量定义为:
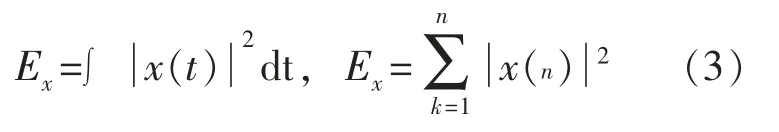
其中,x(n)为信号的离散形式,能量定义为各数值点幅值的平方和。第i 个IMF 分量的能量与所有IMF 分量能量之和的比值定义为公式(4),n 为IMF 的个数。
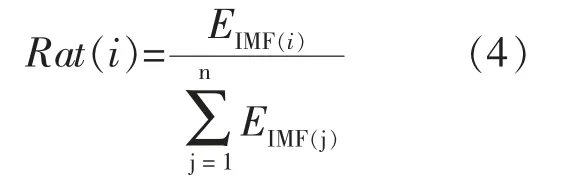
3 数值仿真验证
为了检验能量比值法的可行性,以信号y(t)为例,采样频率10 000 Hz,采样点数5 000 个点。
y(t)=0.6cos(640×π×t)+cos(320×π×t)+0.5sin(80×π×t) (5)
对公式(5)的信号进行EMD 分解,结果如图4所示。
采用能量比值法对图4 中的各IMF 分量分别进行计算,结果列于表1 中。
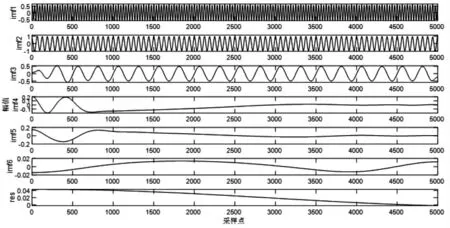
图4 信号的EMD 分解图

表1 各IMF 分量的能量比值表
从表1 中可以得到,前三个有效分量的能量比值均较大,其余虚假分量的能量比值较小,他们之间相差两个数量级,有的甚至高达三个数量级,能量对比明显,可对虚假分量进行准确识别。
4 结语
首先本文对EMD 方法及其虚假分量问题进行了详细的分析,并指出了现有处理方法的优缺点。接着由于虚假分量主要是因为停止准则、 插值误差和端点效应的问题而产生,故虚假分量的幅值和频率较低,能量较小。 最后根据分析结果提出能量比值法,并进行数值仿真验证, 仿真结果表明该方法具有可行性。
