基于投影寻踪权重优化的水资源承载力评价模型
2021-05-19金菊良刘东平周戎星张礼兵吴成国
金菊良,刘东平,周戎星,张礼兵,崔 毅,吴成国
(1.合肥工业大学土木与水利工程学院,安徽 合肥 230009;2.合肥工业大学水资源与环境系统工程研究所,安徽 合肥 230009)
水资源承载力作为衡量水资源可持续发展的重要指标,日益受到更多学者和相关管理部门的重视。有效合理地评价区域水资源承载力可为水资源承载调控、促进区域经济健康发展、保证社会稳定和维持生态环境健康提供参考依据,还可为水资源可持续开发利用提供理论支撑。水资源承载力的概念提出于20世纪80年代末,随后众多学者对其进行了大量研究[1-2],并提出了相应评价方法。作为水资源承载力评价模型构建过程中的重要一环,合理确定权重十分重要,关系着评价结果的可靠性。目前,常用的定权方法或是通过单一方法确定权重,或是没有考虑评价指标间的相互作用[3],均存在或多或少的问题。如:主成分分析法[4]需对原始变量做降维处理,有时主成分的含义较为模糊,导致其分级标准难以划分;专家打分法是专家直接依据相关经验给出权重,存在一定的主观随意性;层次分析法(analytic hierarchy process, AHP)、模糊综合评价法在解决多目标、多层次及多准则等决策问题上存在优势,但人为干扰使得评价结果往往主观性较强,在一定程度上存在不确定性[5];基于特征向量的最优综合评价方法是较为客观的评价方法,但受模型本身限制,在处理类似水资源承载力评价等具有高维度、非线性和非正态特性的评价问题时适应能力低,往往不易取得较为准确的评价结果[5];投影寻踪(projection pursuit, PP)方法不仅能在一定程度上解决数据的高维及非线性问题,还能充分挖掘数据本身的特征[6],但有时会出现确定的客观权重与主观认知明显不一致的情况。
集对分析概念由我国学者赵克勤[7]于1989年提出,其基本思想是针对要研究的问题构建具有一定联系的由两个集合构成的集对,对集对中两集合间的关系特征进行同一、差异、对立三方面的系统分析;然后用联系数对这些关系特征进行定量表达,并可根据集对的联系数进一步计算出相应指标的减法集对势(subtraction set pair potential, SSPP)。减法集对势可克服除法集对势存在的不稳定现象,同时也符合集对势函数表达所研究集对当前确定性状态和未来发展趋势的特性,为集对势应用于多属性动态决策问题提供了理论依据[8],且减法集对势较为客观,计算简便,能够对所研究问题进行定量表达,适用于区域水资源承载力评价问题[9-10]。
为此,本文结合AHP法确定的权重(以下简称“AHP权重”),采用PP法进一步挖掘数据本身特征、优化AHP权重,并在此基础上结合减法集对势理论,构建基于PP-AHP方法定权的水资源承载力评价模型(以下简称“本文模型”),并以安徽省水资源承载力评价为例对模型的有效性进行验证。

表1 评价指标分级标准
1 模型构建
本文模型构建包括以下6个步骤:
步骤1构建评价指标体系,确定相应评价标准。目前,针对水资源承载力评价这一问题,尚无统一的评价指标体系[11]。根据前人建立评价指标体系的经验,基于科学性、整体性、区域性和可操作性[12]等指标体系构建标准,从水资源承载力3大子系统[13]中选出15个指标[14-16](这15个指标已在多种水资源承载力评价模型中使用,符合相应区域水资源承载力评价要求)构建本文水资源承载力评价指标体系(图1),并参照文献[16]中的方法构建评价等级标准,详见表1。

图1 水资源承载力评价指标体系
步骤2构造评价标准等级样本值。为确定各指标的权重,在表1各指标的3个标准等级区间中各线性内插9个评价标准等级样本值,加上表1给出的2个临界值,得到标准样本{xij|i=1,2,…,m+2;j=1,2,…,n}(其中m为插值个数,n为评价指标个数)及其对应的水资源承载力经验等级{yi|i=1,2,…,m+2}。
步骤3标准样本值无量纲化。为消除量纲影响,对标准样本中的正向指标(指标数值随承载力等级增大而增大)和负向指标(指标数值随承载力等级增大而减小)分别采用式(1)和式(2)进行无量纲化处理:
(1)
(2)
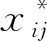

(3)
式中aj为向量a的第j个分量。
在进行综合投影时为挖掘承载力评价指标与评价等级之间的相关性信息,希望投影值zi与经验等级yi相关系数的绝对值|R|尽可能大,因而投影指标函数[17]可构造为
maxQ(a)=|R|
(4)
为挖掘AHP法权重的不确定性信息,本文进一步用PP法优化AHP权重。为了简便、不失一般性,根据文献[14,16]中AHP权重结果,将本文所要求解的权重限定在合理的经验值范围内,再根据投影方向与权重的关系确定投影方向的变化范围,最后结合PP法进行优化,进而确定权重。基于本文权重求解的需求,式(4)所示投影指标函数的约束条件可设为
(5)

步骤5指标值联系数的确定。根据文献[18]中的式(12)~(16)求得各评价指标值x′ij(样本原始数值)隶属于模糊集k(k=1,2,3)的相对隶属度vijk,再将vijk代入式(6)可得样本i的评价指标值联系数[19]。
(6)

步骤6减法集对势的计算。结合步骤4、5,计算出样本i的减法集对势值Sfi:
(7)
据此可判断样本所处的承载力等级。参照“均分原则”[7],Sfi可划分为如下5个势级[14,19]:-1.0≤Sfi<-0.6为反势,-0.6≤Sfi<-0.2为偏反势,-0.2≤Sfi≤0.2为均势,0.2 安徽省位于长江、淮河中下游,与鲁豫鄂赣浙苏6省交界,地跨两带,北部属于温带季风气候,南部属于亚热带季风气候。由于全省常年受季风影响,导致全年降水量在时间和空间上分布较为不均[20],时间上主要表现为春夏季降水量明显多于秋冬季;区域上则为皖南地区降水量和水资源占有量明显高于皖北及皖中地区。全省水资源开发程度较高,但存在人均占有量不足等问题,整体水资源承载情况不容乐观。 为验证本文模型的适用性和可靠性,依据建模6个步骤和图1中的评价指标及表1的等级标准对安徽省2005—2015年水资源承载力进行评价。表2为2007年、2010年和2013年各指标值联系数。将表2中各指标值联系数及步骤4求得的权重代入式(6)和式(7),可得各年份指标值的联系数及相应减法集对势值Sfi,同时参照文献[16],结合表1等级标准划分依据,等级阈值记为s1、s2,将其对应的减法集对势值设为新的评价标准中的1.5级和2.5级,建立减法集对势和等级值的对应关系函数,将2005—2015年的减法集对势值代入可得2005—2015年的评价等级值,由此可得各年份最终评价等级如表3所示。 表2 部分年份评价指标值联系数 表3 安徽省水资源承载力评价结果 2.2.1权重对比分析 为了进一步对PP-AHP方法求得的权重(以下简称“PP-AHP权重”)与基于专家打分的AHP权重[11,13]进行对比分析,将两种方法得出的权重结果列于表4。由表4及相关计算结果可知:①AHP权重由于受人为主观判断的不确定性影响,部分指标如x1和x2,x6、x8和x10等的权重存在完全相同的状况,说明AHP权重在反映多目标、多层次、多准则实际系统的复杂情形时相对比较粗糙,而PP-AHP方法可对指标权重进一步优化、细化;②PP-AHP权重是在基于专家经验的AHP权重基础上,利用PP法进一步优化而得,这一权重求解方法将AHP专家经验定权与PP法客观定权紧密结合,既保留了贴近实际情况的优点,又避免了人为过度干预的缺点;③根据PP-AHP权重结果,对研究区水资源承载力影响最大的5个指标依次为x1、x2、x8、x9和x3,支撑力子系统对应的权重为0.357 4,压力子系统对应的权重为0.424 7,调控力子系统对应的权重为 0.217 8,由此可见,压力子系统在安徽省2005—2015年水资源承载力评价中占比最大,故压力子系统是对安徽省水资源承载力影响最大的子系统;④根据相关权重计算结果可得,PP-AHP权重对应的目标函数值为0.944,AHP权重对应的目标函数值为0.941。由于相关系数越大权重越优,故PP-AHP权重较AHP权重更接近最优解,表明了本文模型定权的合理性和有效性。 表4 两种方法得到的权重结果对比 2.2.2评价等级分析 为进一步对本文模型进行验证,选用文献[14,16]中联系熵方法和平均联系数模型的评价结果与本文模型计算结果进行对比,3种评价方法评价结果见图2。 图2 3种评价方法评价结果比较 a. 总体上,3种方法得到的评价结果虽在部分年份有一定程度的波动(主要是由不同评价方法下某些评价指标的权重差异所致),但总体均是呈转好趋势,整体趋势的变化间接说明了本文模型的评价结果与联系熵方法、平均联系数模型相一致。其中,本文模型与联系熵方法反映的水资源承载力等级变化趋势是一致的,而联系熵方法评价等级普遍略低于本文模型,说明联系熵方法反映的结果较为乐观,而本文模型对水资源承载力的评价更为谨慎。3种方法水资源承载力评价等级相近,但本文模型与平均联系数模型在2008—2009年等级趋势判断上相反,由于安徽省2008—2009年水资源承载力的各项评价指标较为稳定,不会导致这种差异产生,应该是年际降水量增加所致,说明平均联系数模型容易受外界因素干扰,不如本文模型的评价结果稳定。 b. 安徽省在2005—2007年水资源承载力相对较差,3种方法评价结果均表明2006年安徽省水资源承载状况最差,2015年最好。水资源承载力的变化情况和安徽省的年均降水量及国家相关政策密切相关。2005—2010年安徽省年降水量总体呈现上升趋势,水资源承载力等级也逐年降低。2006年后,随着国家加大水资源保护力度、推行节水政策,安徽省水资源承载力大大增强。2011—2013年随着我国经济的高速发展,相应的传统工业和基建规模加大,且降水量略有降低,水资源承载力出现了小幅波动,但并未恶化。2014年和2015年降水量大幅增长,安徽省水资源承载力继续逐步提高,于2015年达到最佳状态。总体上看,安徽省水资源承载力呈现出波动向好的发展趋势,这也与我国对环境及水资源重视程度加大的国情相符。 c. 在与其他模型一致的基础上,本文模型的评价结果波动情况较联系熵方法和平均联系数模型更加平稳,也更符合在相关部门的治理下水资源承载力呈现稳中向好发展的实际情况,表明本文模型在水资源承载力评价中,抗干扰能力更强,不易出现异常的波动和变化。 本文提出了PP-AHP方法求解各评价指标的权重,再将其与减法集对势理论结合,据此构建了基于PP-AHP方法定权的水资源承载力评价模型。与传统的PP法相比,PP-AHP方法求得的权重不仅可以有效避免客观定权与主观认知不符的情况,还可以降低主观定权方法的随意性,较好地综合了专家的主观判断结果与数据本身的特点,能够为相关问题的进一步分析与评价提供可靠的数据,为权重的确定提供了一种新的思路。模型在安徽省水资源承载力评价中的应用结果也进一步验证了PP-AHP方法的准确合理性。本文模型不仅可用于区域水资源承载力评价问题,其在水资源空间均衡、黄河流域生态保护和高质量发展等评价问题中也具有应用前景。2 实例验证
2.1 计算结果
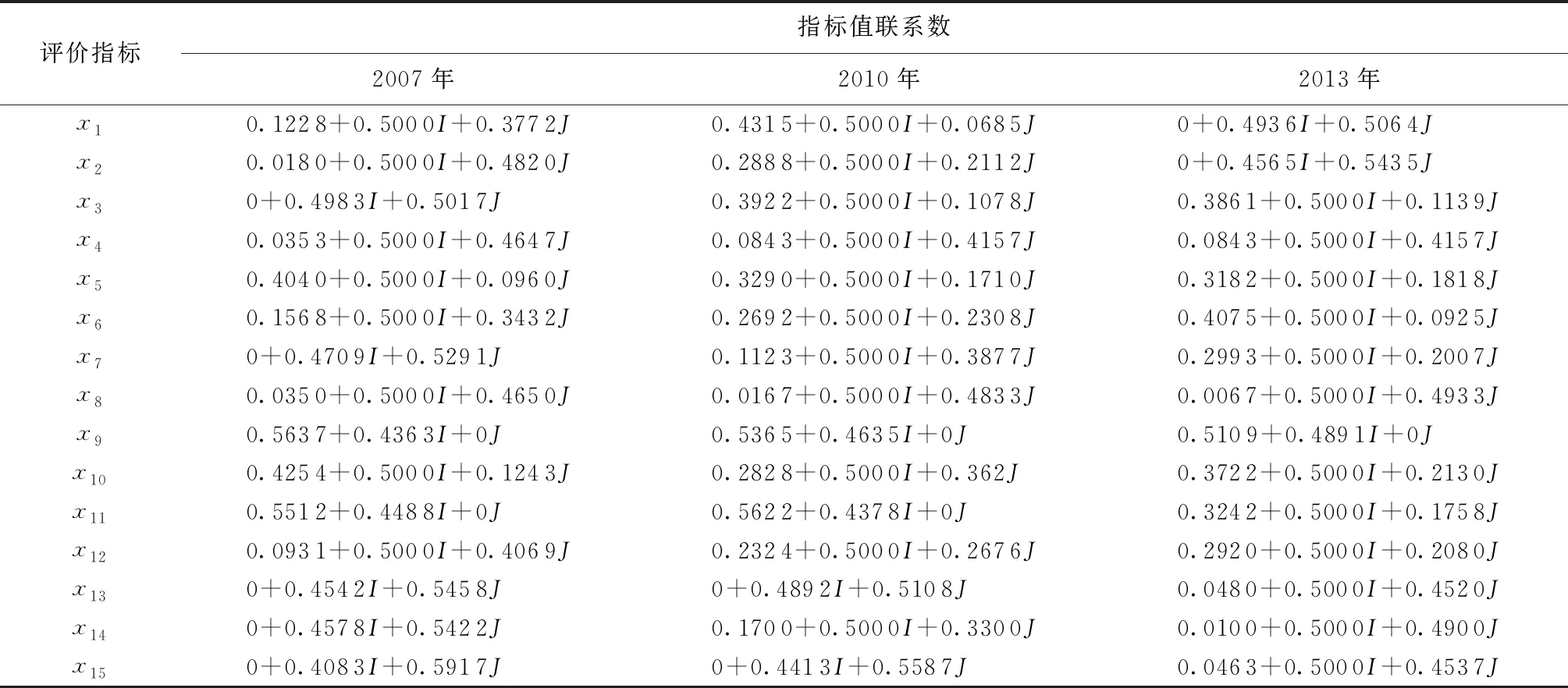

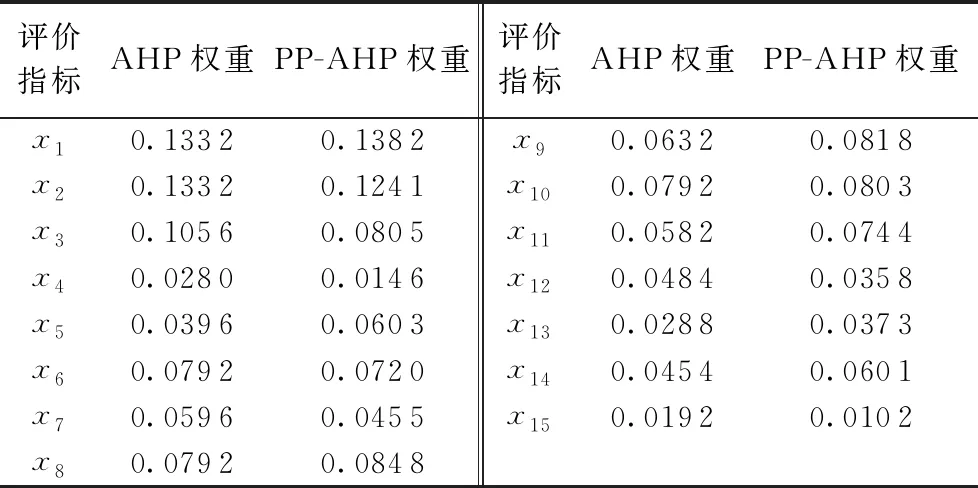
2.2 结果分析
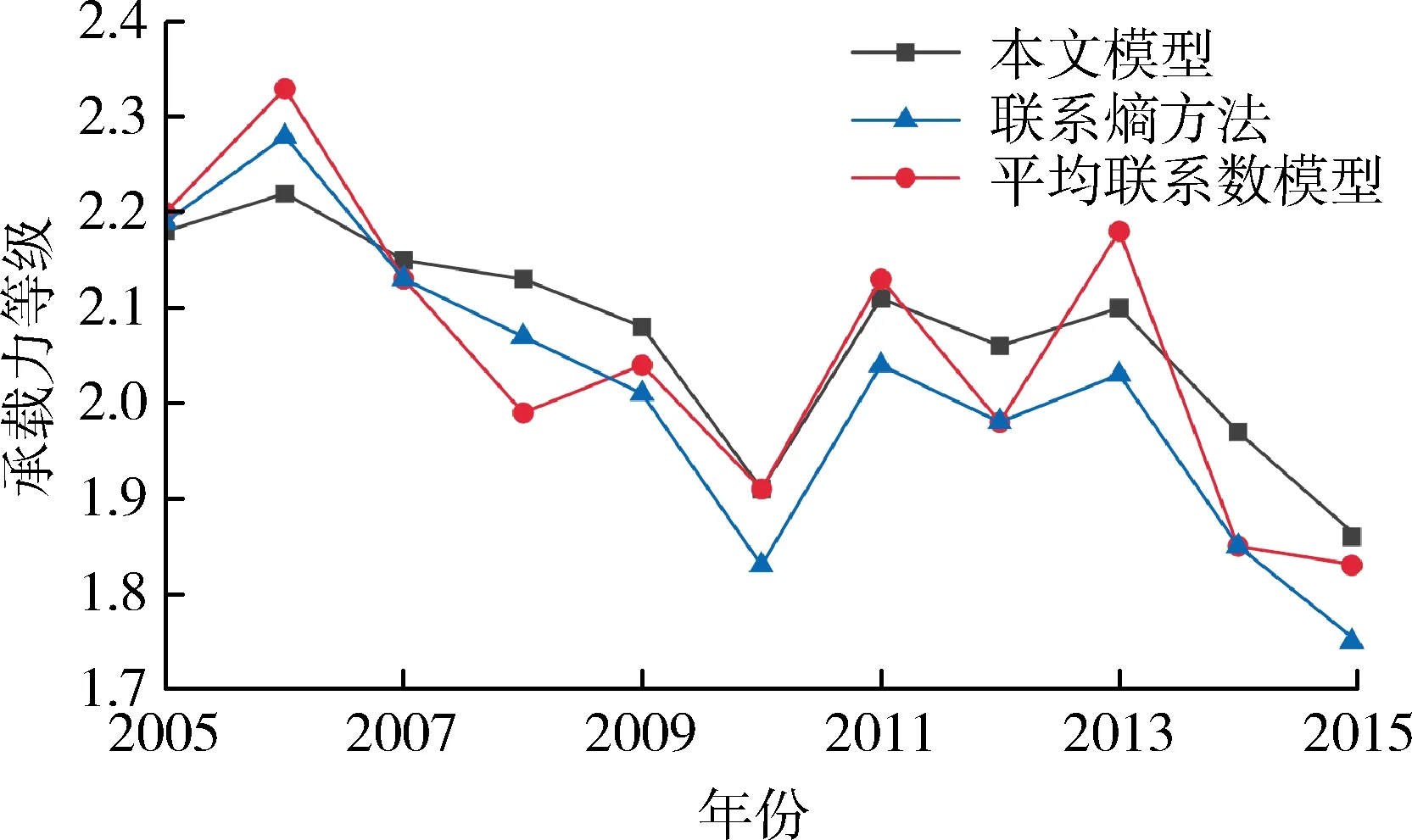
3 结 语
