同模异腔注塑模浇注系统优化分析

2021-05-19秦春节程江帆

浙江工业大学学报 2021年3期

秦春节，程江帆

(浙江工业大学机械工程学院，浙江杭州 310023)

对于多型腔模具，为了保证各个型腔注塑件的质量均匀一致，理想状态是在注塑成型的充填过程中，确保各个型腔的温度和压力相同。同模异腔注塑模是比较复杂的多型腔注塑模，各个型腔注塑件的几何尺寸和质量有差异，注塑过程中较易产生熔液流动不平衡，导致注塑件产生短射、飞边、流痕、熔接痕和翘曲变形等缺陷[1]，从而影响产品质量。

针对注塑件的质量变化，Lee等[2]运用CAE技术把充填模拟和保压模拟结合起来，完善浇注系统设计，使各个型腔充填时间一致、充填压力均匀，实现型腔内熔液流动平衡；Young[3]运用填充时间差和温差等因素构建目标函数，采用遗传算法对浇口位置进行优化，实现充填过程的平衡；罗广思等[4]提出先布置好流道和型腔，然后进行流动模拟，运用模拟结果，调节流道尺寸和浇口尺寸，较好地解决非平衡布置多型腔注塑模的流动平衡问题；倪昀[5]和田冰等[6]基于Moldflow平台对比不同流道的设计方案，以浇注系统的流动平衡为目标进行优化设计；刘磊[7]设定优化目标，采用正交试验法，通过多次模拟，获取最优工艺参数。因此，解决同模异腔模具流动不平衡问题的关键，就是使熔液充填不同型腔时，在同一时间充满，且型腔内的压力均匀分布。结合国内外关于同模异腔注塑模流动平衡问题的研究成果及现状，以某汽车空调风扇端盖注塑件模具为例，运用Moldflow CAE技术，选取模温、料温、注射时间、速度/压力切换时的压力为优化变量，以流动平衡为目标函数，改进与优化端盖注塑件模具的几何参数和工艺参数，对指导生产具有重要意义。

1 浇注系统几何参数设计

汽车空调风扇端盖注塑件为配合安装件，外形、体积和质量均有较大差异且结构复杂。由于浇注系统的几何参数(流道尺寸和浇口位置等)对注塑件填充流动平衡性的影响比较大，一般浇注系统的设计是先确定浇注系统的几何参数，再确定浇注系统的工艺参数[8-9]。该端盖注塑件模具为一模两腔布局，一左一右，热流道采用的是YUDO TINA AM系统。在模具布局确定的情况下，流道布局和长度也已确定，可以调整改进的是浇口位置与流道截面尺寸。

1.1 浇口设计

注塑件注塑生产时，浇口位置的选取是否合理，很大程度上决定了熔体在型腔内的方向性和平衡性[10-11]。该端盖注塑件为尺寸较大的薄壁塑件，若采用一个中心浇口进胶，流长比过大会导致翘曲变形过大。根据注塑件结构特点和模具的热流道结构，采用4 个浇口。

基于CAE软件Moldflow平台，对注塑件浇口位置进行分析，流动阻力指示器显示注塑件的上表面流动阻力小、壁厚均匀，因此浇口位置选在此处，4 个浇口均匀分布，确保熔体速度和行程基本一致。此外，考虑注塑件的表面质量要求，选择点浇口进胶。点浇口直径取注塑件基本壁厚1.5 mm的0.5～2 倍，取整为φ 2.5 mm。

1.2 流道设计

流道设计是注塑成型模具的核心，流道设计主要考虑流道排布、流动阻力和截面形状3 个方面[12]。

利用Moldflow平台的流道系统平衡分析，建立了一个端盖注塑件模具的流道平衡分析模型，在设置好参数约束条件下，进行自动迭代计算，达到流动平衡状态后，生成流道截面尺寸。迭代计算开始时，端盖的流动不平衡率为10%左右，迭代计算结束后流动不平衡率为5%左右。图1给出了注塑工艺参数。流道平衡参数设置主要考虑注塑件的注塑时间与压力的收敛差。

图1 注塑工艺参数设置Fig.1 Parameter setting of filling process

迭代计算的结果是生成一个具有新流道尺寸的模型。对该模型的流道截面尺寸取整，结果见表1。浇口参数：浇口形式为点针阀，尺寸为小端φ 2.5 mm，长度为3 mm，数量为8。

表1 优化后各级流道取整尺寸表Table 1 The size table of optimized flow channels

根据Moldflow模拟注塑，进一步确认几何参数的改进效果。端盖注塑件的压力分布见图2，流道优化后的两端盖不仅各自压力分布均匀，且彼此非常接近，因而端盖注塑件有较为一致的体积收缩率，翘曲变形减小。

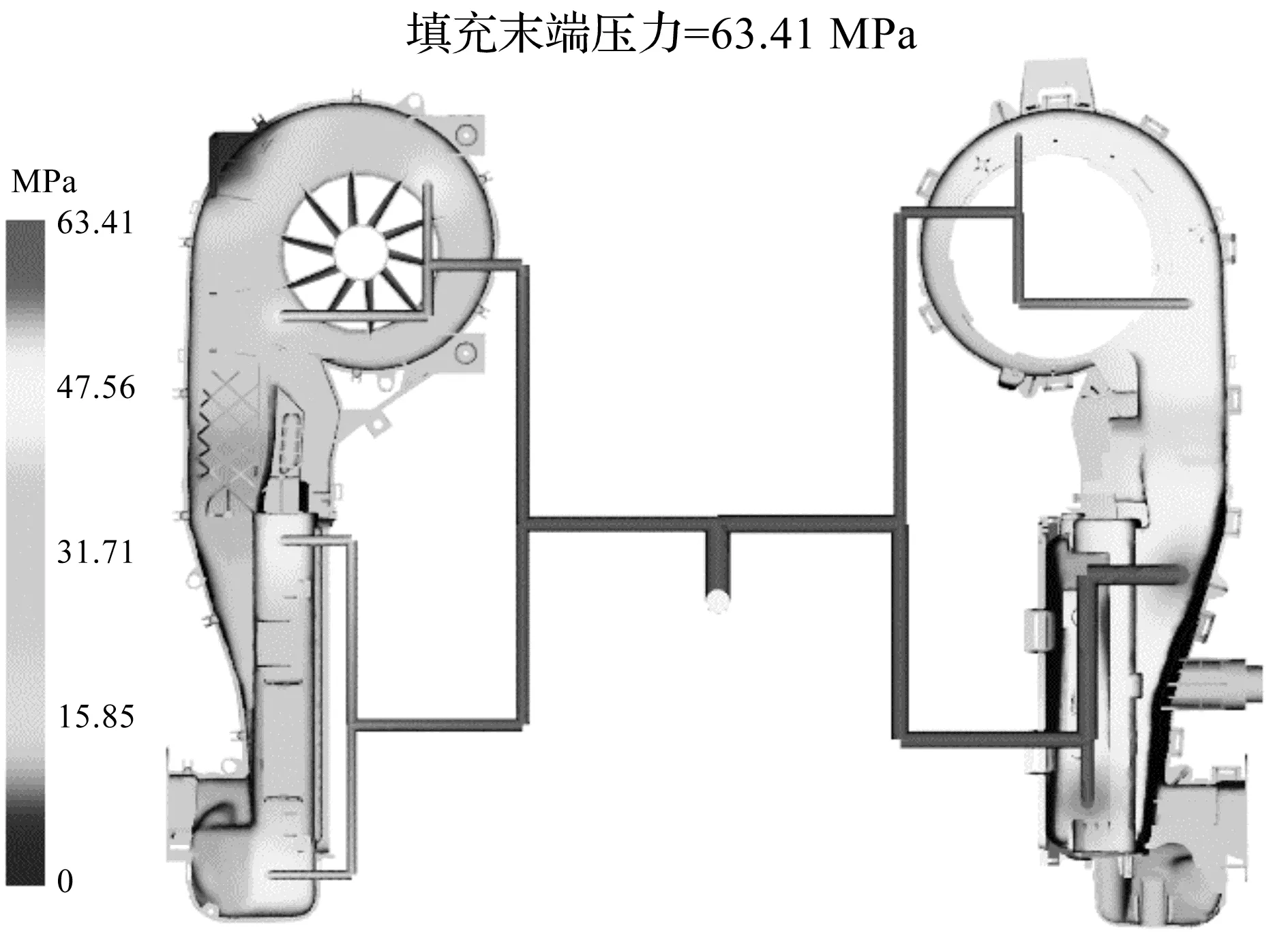
图2 填充末端压力图Fig.2 Pressure diagram of fill end

2 浇注系统工艺参数优化

在浇注系统优化过程中，一般采取粗调-微调的方法，即先对浇注系统的几何参数进行改进设计，再对其工艺参数进行优化设计[1]。因此，在完成该端盖注塑件模具浇注系统几何参数改进设计后，需要进一步优化其工艺参数。

2.1 响应曲面试验设计

响应曲面法(Response surface methodology，RSM)是一种优化方法，它通过数学和统计方法相结合，对所研究的对象进行建模和分析[13]。响应曲面法常见的方法有中心复合设计(Central composite design，CCD)和Box-Behnken设计(Box-Behnken design，BBD)[14]。

运用响应曲面法的中心复合设计时，若变量太多，则工作量过大，导致效率降低[15]。因此，综合考虑模温A、料温B、注射时间C、速度/压力切换时的压力D这4 个工艺参数是决定端盖注塑件填充不平衡率的首要因素，根据端盖注塑件的材料参照推荐来获取相应参数，将这4 个工艺参数进行编码设计，见表2。

表2 因子及其编码水平Table 2 Factor and its coding level

优化分析中，优化目标是流动不平衡率，优化变量是模温A、料温B、注射时间C、速度/压力切换时的压力D这4 个工艺参数。根据4因素进行30次参数组合试验，结果如表3所示。

表3 设计表格(随机化)Table 3 Design form (Randomization)

根据表3，在Moldflow平台运行填充分析，得到不同数组对应的目标值，从而设计响应曲面实验方案，如表4所示。

表4 响应曲面试验设计方案Table 4 Response surface test design scheme

2.2 响应曲面分析

通过对实验结果进行残差值检验和方差分析，给出可靠的优化结果。

方差分析表示评估优化变量对目标函数的影响大小，即优化模型的显著性。一般用P值来确定可信度，P=0.05是边界线。当P<0.05，表明优化变量对优化目标影响显著；当P>0.05，表明优化变量对优化目标影响不显著。通过残差值检验和方差分析去掉不显著项；多次检验分析，直到满足优化模型试验要求[13]。

流动不平衡率的方差分析如表5所示，其中均方差S=0.297 49，PRESS=0.435 7。表中回归、平方和交互作用的P值均较小，验证了各类参数项影响显著。从代表优化模型可靠度的R-Sq=90.75%，R-Sq(预测)=90.95%，R-Sq(调整)=93.77%来看，数值都在90%以上，证明优化模型有效。

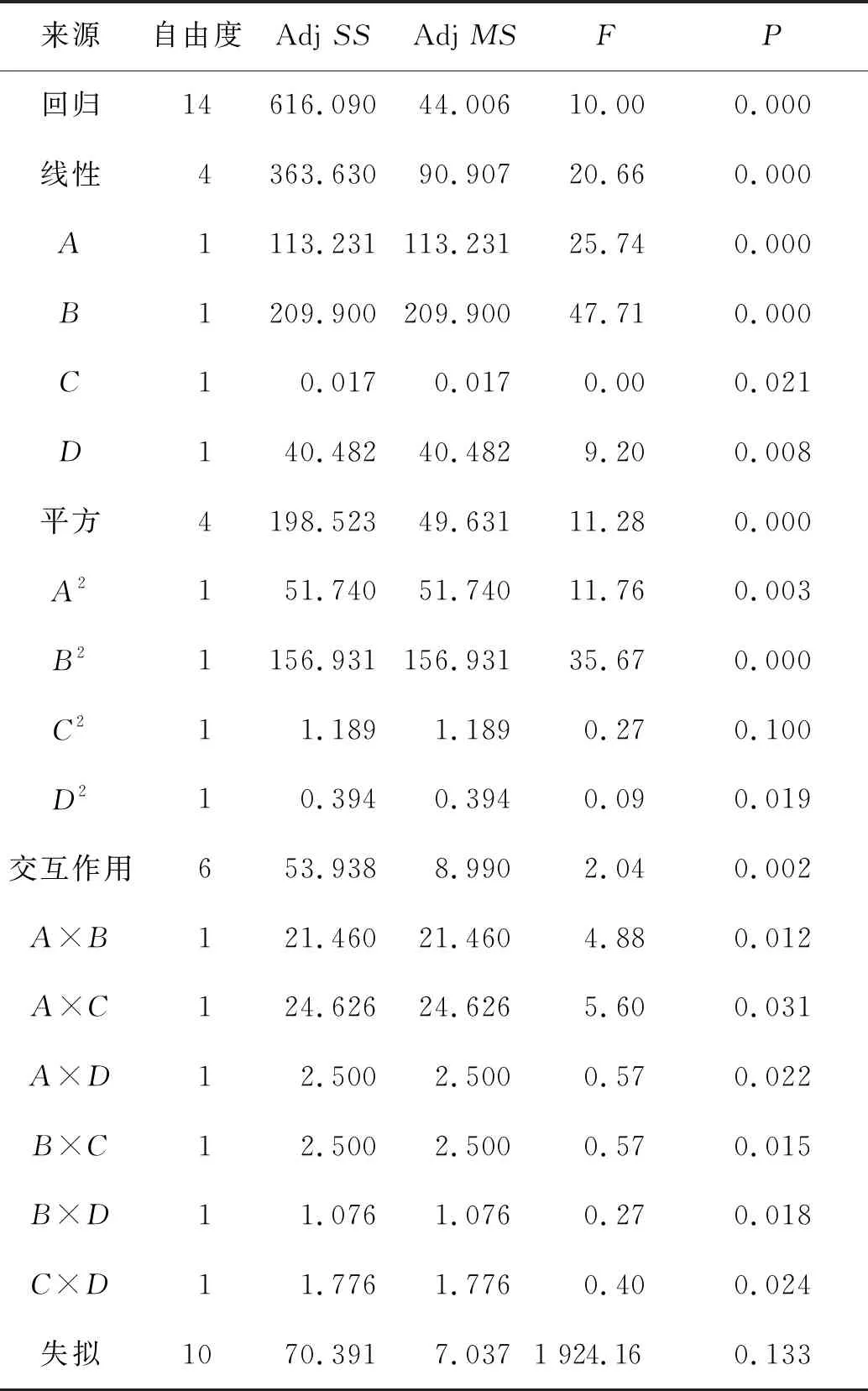
表5 流动不平衡率的方差分析Table 5 Variance analysis of flow unbalance rate

图3是流动不平衡率残差图：图3(a)中各组实验点拟合成直线；由图3(b)可知残差值随机分布，无规律性；由图3(c)可知残差呈正态分布；图3(d)中残差有正负，说明优化模型具有独立性。通过分析表5和图3，说明优化模型拟合效果好，接下来进行微调，即进行端盖注塑件模具工艺参数的优化设计，运用Minitab响应优化器求解最优工艺参数。设置注塑流动不平衡率的优化目标值为0，寻优求解如图4所示。优化的工艺参数为：模温35 ℃、料温220 ℃、注射时间1.5 s、当速度/压力切换时的压力为98.26%时，流动不平衡率为0，获得理想效果。