光储直流配电网灵活虚拟惯性控制策略

刘英培，周素文，梁海平，唐晓骏，马世英，谢 岩

（1. 华北电力大学 电气与电子工程学院，河北 保定071003；2. 中国电力科学研究院有限公司 电网安全与节能国家重点实验室，北京100192）

0 引言

随着常规化石能源的短缺和环境污染问题的凸显，人类已经意识到能源的利用和开发必须从传统化石能源向风能和太阳能等分布式能源过渡［1］。随着分布式能源大量接入电网，传统交流电网在消纳大规模分布式能源方面越来越力不从心［2］。

目前，直流配电网已成为众多方案中解决该问题的研究热点［3］。直流配电网相比于交流配电网，没有频率和功角问题，且具有输送容量大、结构简单、传输损耗低和控制灵活等优势［4］。此外，光伏等分布式电源为直流电源，采用直流电网可以大幅减少DC／AC 换流器的使用，节约成本，提高电网可靠性［5］。但是，直流配电网的电容惯性远小于交流配电网中同步发电机所具有的机械惯性［6］。当直流配电网中功率有较大波动时，直流母线电压也会随之有较大波动，这给电压敏感的负荷和分布式能源带来了不利的影响［7-9］。而且，间歇性光伏发电单元产生的阶跃变化和随机波动会导致直流母线电压和配电网的功率发生剧烈波动。直流配电网中换流器普遍采用电压下垂控制，通过发生扰动时功率的自动分配来确保其电压稳定［10］。但是，在功率波动时，换流器的输出功率必须根据下垂曲线来接近新的稳定工作点。因此，当直流配电网中有明显的功率不平衡时，仅凭借直流电容不能有效地减小直流电压的突变率，必须将虚拟惯性控制引入直流配电网来提高其电压质量。

虽然电力电子换流器使得风力发电机的机械和电气系统之间解耦［11］，阻止了风机响应系统电压变化，但是可以通过附加惯性控制器释放风机转子中存储的动能，增加电网惯性，平抑电压波动。文献［5］通过在风机上附加虚拟惯性控制策略，有效地解决了风电输出功率不确定带来的直流电压波动的问题。而光伏属于非旋转静止元件，无法像风机一样平抑电压波动［12］。文献［13］通过让光伏单元偏离最大输出功率点来调节功率产生虚拟惯性。该方法虽然增大了系统惯性但没有充分利用光伏发电，降低了光伏发电效率。将光伏单元与一定的储能单元相结合，可以减小光伏功率的波动对电网的影响。但随着光伏渗透率的不断提高，光储静止元件缺乏惯性是无法忽略的问题［14］。因此，充分利用储能快速充放电的能力为系统提供惯性支持对保证光伏发电效率、提高直流电压稳定至关重要。

考虑到直流配电网储能设备的潜在惯性支持能力，本文提出了一种蓄电池提供灵活虚拟惯性的控制策略。首先，建立了蓄电池荷电状态（SOC）与直流电压的函数关系表达式，在此基础上提出了一种蓄电池产生灵活虚拟惯性的控制策略；然后，考虑了蓄电池的充放电极限问题，通过划分蓄电池工作区并引入反正切函数来限制其过度充放电；最后，采用小信号稳定性分析研究蓄电池采用虚拟惯性控制的直流配电网稳定性问题。

1 光储直流配电网结构

本文所研究的光储直流配电网拓扑结构如附录中图A1所示，该系统主要由光伏单元、储能单元、交流负荷和交流电网四部分组成。

（1）光伏单元：采用单向DC／DC 换流器（即图A1 中PV-DC）接入直流配电网，运行时采用最大功率点跟踪（MPPT）控制，特殊情况下（如电压过高）也可以采用降功率方式运行。

（2）储能单元：通过双向DC／DC 换流器（即图A1 中B-DC）接入直流配电网，换流器按下垂控制进行直流电压调节。本文选择较为经济的铅酸蓄电池作为储能元件。

（3）交流负荷：通过电压型DC／AC 换流器（即图A1 中L-VSC）接入直流配电网，其由恒功率负荷组成。

（4）交流电网：在电压型DC／AC 换流器（即图A1 中G-VSC）的控制下，按照下垂控制完成交直流功率交换和直流电压调节。

2 直流配电网的虚拟惯性控制

2.1 直流配电网惯性的定义

在交流系统中，惯性反映了系统在阻止频率发生突变方面的能力［15］。交流同步发电机的惯性时间常数Hs一般定义为［5］：

其中，Wk和SN分别为额定转速下转子中储存的动能和发电机的额定发电容量。

与交流系统类似，直流系统的惯性反映了系统在抑制电压发生突变方面的能力［16］。类比式（1），直流电网中的惯性时间常数Hdc可定义为［17］：

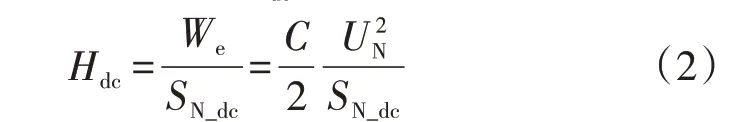
其中，We为直流母线在额定电压下其电容中储存的电能；SN_dc为直流母线额定功率传输容量；C和UN分别为直流电网的电容和直流母线的额定电压。

实际直流电网的电容C很小［5］，从式（2）可知配电网在受到一定的扰动时惯性较小，导致电压波动较大，因而对其电压质量产生了重要影响。

2.2 直流配电网虚拟惯性分析

图1 给出了直流配电网中换流器直流侧的等效电路。图中，PR和Ps分别为新能源发电单元及负荷单元需要的总功率和某一功率源（如储能单元等）提供的功率；PC和udc分别为流入直流侧电容的功率和直流电压。

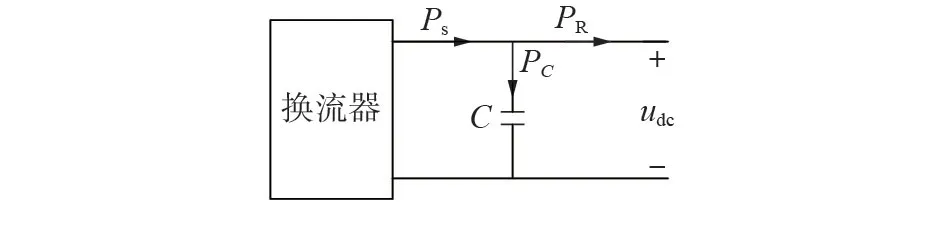
图1 直流电容侧的功率关系Fig.1 Power relationship of DC capacitor side

由图1可得：

由式（3）易知，当直流电压保持恒定时，换流器直流侧电容不充电也不放电，应有Ps=PR成立。当电网功率发生波动时，直流电容越小，电压变化率就越大，进而电压波动得越严重。

由于直流配电网中电容很小，这使得系统受到扰动时电能质量较差。可通过在换流器上施加控制策略，以达到在直流侧并联虚拟电容的效果。

当直流电压变化时，换流器采用虚拟惯性控制可使功率源提供辅助功率ΔPs，ΔPs可表示为［18］：

其中，Cvir为在换流器直流侧施加虚拟惯性控制产生的虚拟电容。

若换流器采用虚拟惯性控制，当负荷功率波动ΔPR时，直流电容侧的功率方程为：

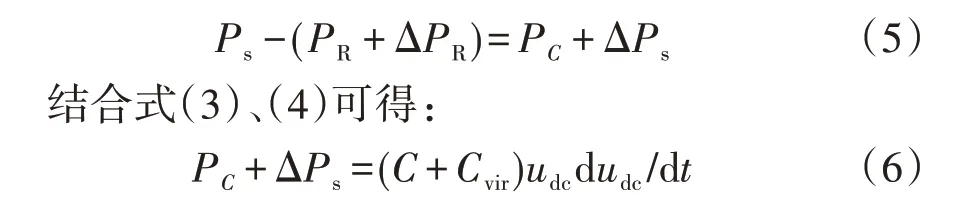
由式（5）、（6）可知，负荷功率波动时，通过附加虚拟惯性控制，直流电网的电容从C增加为C+Cvir，解决了实际直流电网中电容过小的问题，从而提高了电压质量。根据式（2）可知，施加虚拟惯性控制时的惯性时间常数为：由式（7）可知，换流器通过虚拟惯性控制增加了直流配电网的惯性时间常数。

2.3 储能元件的虚拟惯性分析

蓄电池正常运行时近似为恒压充放电。当蓄电池充满电时，其额定容量为QN，蓄电池放电过程中电流为iB，则SOC值γsoc可表示为［19-20］：

其中，Qr为蓄电池的剩余电量。

结合式（8），蓄电池存储的能量WB可表示为：

其中，uB和γsoc_0分别为蓄电池的电压和初始SOC。

蓄电池通过建立γsoc与直流电压udc的函数关系，可以实现在电压波动时快速吸收或释放能量，增加电网惯性和减缓电压波动的目的。

为了建立上述函数表达式，让蓄电池发出（吸收）的能量等于虚拟电容发出（吸收）的能量，即：

根据式（9）和式（11），蓄电池换流器产生的虚拟电容为：

其中，Δγsoc和Δudc分别为蓄电池SOC 变化量和直流电压变化量；kB=(Δγsoc/γsoc_0)/(Δudc/udc)，为蓄电池SOC变化率与直流电压变化率的比值。

通过式（12）可知，蓄电池虚拟惯性大小不仅取决于直流电网的电容C，还取决于蓄电池SOC 变化率与直流电压变化率的比值kB和蓄电池存储的能量WB与电容存储的电能We的比值。通常蓄电池存储的能量大于直流电容存储的电能，即WB/We>1。若蓄电池SOC 变化率远大于直流电压变化率，即|kB|≫1，则经过蓄电池的快速吸收或释放能量，可虚拟出比直流电容更大的惯量。

3 光储直流配电网灵活虚拟惯性控制策略

本文在传统下垂控制的基础上，根据式（12）所定义的虚拟电容表达式，提出模拟电容充放电的灵活虚拟惯性控制策略。即将电压波动信号引入蓄电池换流器控制部分，通过附加灵活虚拟惯性控制来改变电流参考值，使蓄电池输出功率迅速发生改变，从而给予电网一定的惯性支持。图2 为蓄电池换流器附加灵活虚拟惯性控制结构图。图中，kE为下垂系数；I*B和U*dc分别为蓄电池电流和直流电压的参考值。

图2 蓄电池换流器附加灵活虚拟惯性控制结构图Fig.2 Structure diagram of additional flexible virtual inertia control for battery converter

拟合曲线表达式如式（13）所示。

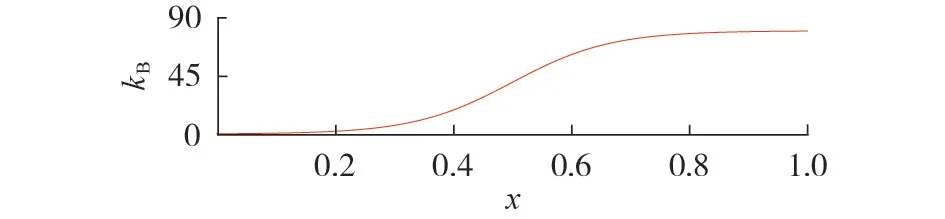
图3 参数kB随电压变化率变化的曲线Fig.3 Curve of voltage variation rate vs. kB

其中，kBmax为kB的最大值，具体取值由第5 节中的稳定性分析确定。

由双曲正切函数曲线可知，当电网在正常运行且电压变化率较小时，kB取值较小，有利于系统的稳定。而当电压变化率较大时，kB的值快速增大，有利于快速调节蓄电池释放能量，减小电压变化。与kB取值不变的固定虚拟惯性相比，基于双曲正切的灵活虚拟惯性控制可以根据电压变化率自适应调节惯性大小，减缓电压波动，提高电压稳定性。但当电压波动较大，蓄电池SOC处于极限状态时，有可能对蓄电池造成损坏，所以需要在虚拟惯性控制策略中考虑SOC。

4 考虑蓄电池SOC的虚拟惯性控制策略

考虑到蓄电池充放电能力对虚拟惯性控制策略而言至关重要，合理使用蓄电池需要确定蓄电池工作区。根据文献［19］，蓄电池工作区可划分为：

其中，a、b分别为放电极限区的上界值和充电极限区的下界值。本文中取a=0.25、b=0.75。

本文中蓄电池SOC的虚拟惯性控制主要是指蓄电池处于充放电极限区，而超出此范围蓄电池不能再进行充放电，否则会影响其寿命，本文不再讨论。

从kB的定义式中可以得到，当直流电压变化一定时，kB越小蓄电池SOC 变化就越少，即蓄电池充放电功率越少。本文通过在极限区建立蓄电池SOC与kB的函数关系，即通过蓄电池SOC 来决定kB的取值，从而达到减少输出功率、保护蓄电池安全稳定的目的。

考虑到反正切函数无限接近最值的特性，本文选择通过反正切函数来建立蓄电池SOC与kB的函数关系，如式（15）所示。

其中，k1和k2为调整系数，需要根据具体实际情况来确定；kB0为蓄电池处于极限区且需要限制充放电时kB的最大值，将在6.4节进行具体分析。

当蓄电池处于充放电极限区时，由于反正切函数的限制，kB随着蓄电池SOC 接近极限而减小，减小了吸收或释放的功率，确保了蓄电池的安全稳定运行。在蓄电池SOC 达到充放电极限区时，需要光伏单元根据电压的偏高由MPPT 转换成降功率运行方式和负荷根据电压的偏低进行减负载，限于篇幅，本文不进行详细讨论。

综上所述，本文所提控制策略中，蓄电池在γsoc∈[0.1，a]且充电电流为正和γsoc∈[b，0.9]且放电电流为正时采用灵活虚拟惯性控制策略；其他情况下采用式（15）所示的考虑蓄电池SOC的虚拟惯性控制策略。

5 虚拟惯性控制策略稳定性分析

由上文分析可知，kB越大，蓄电池所提供的虚拟惯性就越大，然而过大的惯性可能会引发系统稳定性问题。为了确定kB的取值范围，需要对采用虚拟惯性控制的直流配电网进行稳定性分析。

5.1 直流配电网小信号建模

以附录中图A1 所示的四端直流配电网为研究对象。

（1）蓄电池换流器的小信号模型。

根据图2，图4给出了储能换流器的小信号控制框图。图中，θ为引入的状态变量。为了便于建模，将高通滤波器进行了等效化处理［15］。

图4 蓄电池换流器小信号控制框图Fig.4 Small-signal control block diagram of battery converter

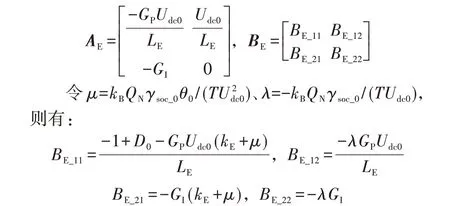
其中，ΔiB、ΔDI和Δθ分别为蓄电池电流、B-DC 占空比D的积分部分和状态变量θ在其稳态值附近的微小变化量；Udc0为直流电压的初始稳态值，其余下标含0的变量含义类似。

（2）光储直流配电网小信号模型。

为了便于分析，假设交流电网为无穷大电源，换流器G-VSC为理想换流器，光伏输出功率PPV和负荷功率PL为常数，忽略线路电阻。直流配电网电流关系图如附录中图A2 所示，根据基尔霍夫电流定律（KCL）可得电流关系为：

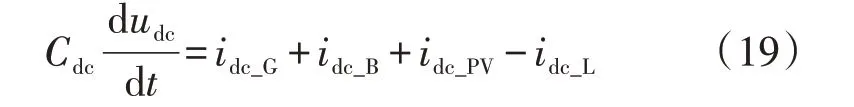
其中，Cdc为直流母线电容；idc_G、idc_B、idc_PV、idc_L分别为交流电网、蓄电池、光伏和负荷的直流侧电流，具体表达式如式（20）所示。

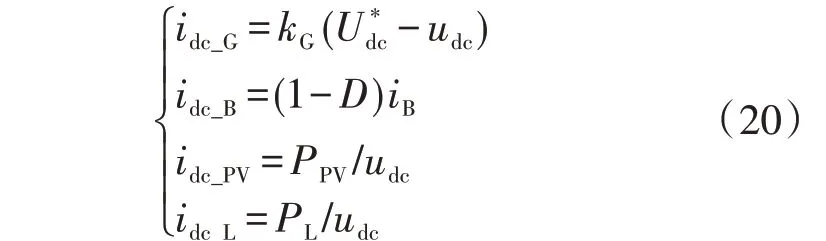
其中，kG为G-VSC的下垂系数。

再根据图5，可得关于θ的方程为：

5.2 光储直流配电网稳定性分析

直流配电网中的元件参数如附录中表A1所示。对5.1节中的小信号模型进行特征根轨迹分析，可得蓄电池换流器附加虚拟惯性控制时，系统随kB变化的特征根轨迹，如图5 所示。图中，kB初值为1，并以1为步长，增加到100。观察图5可知，随着kB的增加，根轨迹逐渐向虚轴靠近，当kB=85 时，出现了实部为正的特征根，系统不稳定。因此当kB小于85 时，附加虚拟惯性控制的光储直流配电网可以稳定运行。

图5 参数kB变化时的根轨迹Fig.5 Root locus with variation of kB

6 仿真分析

本文利用MATLAB／Simulink 仿真软件搭建了如附录中图A1 所示的四端直流配电网仿真系统。仿真过程中光照强度恒为1 000 W／m2，温度恒为25 ℃，光伏运行在MPPT状态，约发出功率16.5 kW。

6.1 电池正常区下负荷突增与突减时的系统惯性响应

（1）电池正常区下负荷突增时的系统惯性响应。

仿真过程中，初始负荷为20 kW，交流电网向直流侧注入功率约2.5 kW，此时电压维持在额定值附近；t=3.5 s 时，交流负荷突增10 kW。蓄电池换流器分别采用无虚拟惯性控制、固定虚拟惯性控制和灵活虚拟惯性控制进行仿真对比。此次仿真中蓄电池初始SOC 为50%，并规定蓄电池放电为其正方向。图6 给出了不同控制策略下的直流电压udc、交流电网输出功率Pg和蓄电池输出功率PB的变化曲线。图中，udc为标幺值，后同。

图6 电池正常区下负荷突增后系统仿真波形Fig.6 Simulative waveforms of system after sudden load increase in normal area of battery

由图6 可知，①当负荷突增，蓄电池采用无虚拟惯性控制时，系统因缺乏惯性，直流电压迅速降低到0.976 p.u.，电能质量较差；与无虚拟惯性控制相比，固定虚拟惯性控制下的电压下降速度得到一定的降低；而采用灵活虚拟惯性控制时，电压下降明显变缓，电压质量得到显著提升。②当负荷突增时，由于采用固定虚拟惯性控制快速释放功率，减缓了交流电网向直流配电网注入功率的上升趋势，对直流电网的功率平衡恢复和电压波动抑制起到了一定的积极作用；而与固定虚拟惯性控制相比，采用灵活虚拟惯性控制进一步减缓了交流电网的功率输出，因此对交流电网稳定性的影响较小。③当负荷突增，采用灵活虚拟惯性控制时，蓄电池能迅速增大输出功率至4.8 kW，比固定虚拟惯性控制时的3.9 kW 大0.9 kW，减少了功率差额，明显抑制了电压突变，使直流电网具有较大的惯性。

（2）电池正常区下负荷突减时系统惯性响应。

仿真过程中，初始负荷为30 kW；t=3.5 s 时，负荷突减10 kW。附录中图A3 给出了负荷突减时的仿真曲线，其与负荷突增时分析过程类似，不再赘述。由图6 和图A3 可知，本文提出的蓄电池附加灵活虚拟惯性控制策略提高了直流配电网的惯性，且通过灵活改变kB的大小，可以迅速吸收或释放蓄电池功率，快速平抑电网功率波动。

6.2 电池充电极限区下负荷突减时系统惯性响应

仿真过程中，t=4.5 s 时，负荷突减20 kW，而且此时蓄电池处于充电极限区，为了更好地展示式（15）中反正切函数对kB的影响，本次仿真中初始SOC设为75%。蓄电池换流器分别采用无虚拟惯性控制、考虑SOC 的虚拟惯性控制和不考虑SOC 的虚拟惯性控制（即kB固定为kB0时的虚拟惯性控制）进行仿真对比。电池充电极限区下负荷突减后系统仿真波形如图7所示。

图7 电池充电极限区下负荷突减后系统仿真波形Fig.7 Simulative waveforms of system after sudden load reduction in charging limit area of battery

从图7 中可以看出，在交流负荷突减时，直流电网因缺乏惯性，直流电压迅速增加到1.029 p.u.；而采用考虑SOC 的虚拟惯性控制时，电压上升趋势得到一定的减缓。与采用不考虑SOC的虚拟惯性控制相比，由于蓄电池处于充电极限区，其充电功率受到反正切函数的限制，所以直流电压曲线上升幅度大，而且由交流电网输出功率Pg曲线可知，此时需要交流电网通过快速减少功率输出来平衡直流配电网的功率过剩。

综上，当负荷突减后，在反正切函数的作用下，蓄电池吸收的功率受到限制，从而保证了在充电极限区下蓄电池的安全和稳定。

6.3 稳定性分析结果验证

从图6 和附录中图A3 所示的仿真结果可知，电网的虚拟惯性随着kB的增大而增大。然而根据本文的稳定性分析可知，kB过大会引起电网稳定性问题，导致系统失稳。图8 给出了系统稳定性测试结果，测试条件与图6一致。

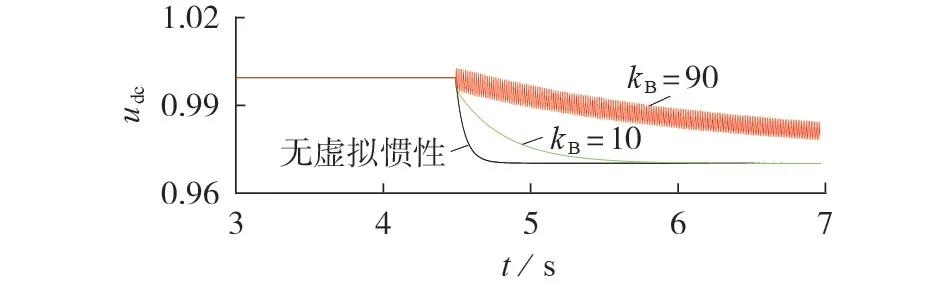
图8 系统稳定性测试结果Fig.8 Test results of system stability

本文通过稳定性分析得到kB的取值范围应小于85，从图8 可知：当kB分别取0 和10 时，随着kB的增大，直流电压更加平缓地降落至稳定值；当kB=90时，直流电压发生高频振荡，系统稳定性遭到破环。因此选择灵活虚拟惯性控制参数时要始终确保kB小于85，以保持系统的稳定。

6.4 参数kB0取值问题的分析

通过附录中图A4 仿真对比kB不同取值下直流电压波动情况，可知其取值为10 时直流电压波动已有明显减缓，继续增大其取值，直流电压波动减弱能力的增幅逐渐下降且电压调整时间逐渐增大。考虑到参数kB0主要针对系统小扰动波动而且还要考虑蓄电池处于极限区时kB的取值不能大，本文综合上述情况选择kB0=10。

7 结论

本文提出了光储直流配电网中蓄电池附加灵活虚拟惯性控制策略，该控制策略对配电网的功率平衡恢复和电压波动抑制起到了一定的积极作用。通过理论推导和仿真验证得到了以下结论：

（1）本文通过建立蓄电池SOC 与直流电压的函数关系，在传统下垂控制上附加灵活虚拟惯性控制来改变蓄电池电流参考值，从而给予电网一定的惯性支持；

（2）一方面提出利用直流电压变化率变化虚拟惯性的灵活虚拟惯性控制策略，另一方面考虑了蓄电池的充放电极限问题，通过反正切函数的作用，避免蓄电池深度充放电，在充分利用其容量的前提下，确保了系统的安全稳定运行；

（3）建立了光储直流配电网小信号模型并对其进行了稳定性分析，明确了参数kB的变化范围以及其对系统稳定性的影响。

附录见本刊网络版（http：//www.epae.cn）。