基于MFO算法的无刷直流电机模糊控制设计

刘雨豪，廖 平

(中南大学机电工程学院，湖南长沙 410083)

0 引言

在运动控制领域，直流电机以其优良的转矩和调速性能得到了广泛的应用[1]。有刷直流电机采用电刷进行机械换向，导致其具有噪音大、寿命短、可靠性差等缺点。随着电力电子技术的不断进步，新型材料和功率开关器件等出现，采用电子换向的无刷直流电机(BLDCM)应运而生。它既克服了有刷直流电机的缺点，又保有了优越的启动和调速性能，在航空航天、国防、工业自动化等领域得到了极快的发展和普及。

现代社会对电机控制性能的要求日益提高，一方面可以优化电机本体结构及相关电力电子装置，另一方面可以使用更加先进的电机控制策略[2-3]。BLDCM是变量复杂、非线性且强耦合的系统，难以推导出精确的数学模型[4]。传统PID控制方法依赖具体数学模型基础，很难满足准确和稳定的控制要求。模糊控制(fuzzy control)模仿人的思维和逻辑推理来进行控制而不依赖确定的控制对象模型，弥补了传统PID的控制短板[5]。但是模糊控制器缺乏参数自调整能力，在包含时变参数的非线性系统中，很难达到最优控制。

近年来，国内外众多专家学者应用智能控制算法优化模糊控制器，管先翠等将微粒群算法(PSO)应用至模糊控制[6-7]，方文茂在遗传算法(GA)优化模糊控制方面也做了大量工作，取得了一定的成果[8]。飞蛾火焰优化算法(MFO)是2015年由S. Mirjalili提出的一种全新群智能仿生算法，相比其他算法具有更优秀的寻优能力[9]。本文提出基于飞蛾火焰算法优化模糊控制的新方法，克服了模糊控制器不能更新控制参数的缺陷，应用MATLAB/simulink对其进行仿真研究，验证了其优越的控制性能。

1 BLDCM的数学模型

无刷直流电机感应电动势为梯形波，且含有较多高次谐波，电感非线性，对其运行特性进行精确分析是非常困难的。本文以两两导通三相星形连接为例，并做出以下假设：

(1)三相绕组完全对称，定子电流、转子磁场分布对称；

(2)气隙磁场为梯形波，平顶宽度120°；

(3)不计磁滞和涡流的损耗；

(4)忽略磁路饱和、齿槽效应和电枢反应。

1.1 定子三相绕组电压平衡方程

(1)

式中：ui为定子各相电压,V；ii为定子各相电流，A；ei为定子各相反电动势,V；Ri为定子各相绕组电阻，Ω；L为定子绕组自感，H；M为定子绕组间互感，H；i=a,b,c。

1.2 电磁转矩方程和机械运动方程

根据能量守恒定律，两方程可分别表示如下：

(2)

式中：Te为电磁转矩，N·m；w为电机输出转速,rad/s。

(3)

式中：TL为负载转矩，N·m；B为阻尼系数，N·m·s/rad；J为电机转子转动惯量，kg·m2。

2 基于MATLAB/simulink的BLDCM控制系统仿真模型

本文基于BLDCM工作原理，在simulink环境下采用模块化建模的方式，将直流无刷电机分离成速度调控、参考电流、电流滞环、电压逆变和BLDCM本体5个模块。系统整体设计框图如图1所示，仿真系统采用双闭环控制方案：外环转速环增强系统抗负载干扰能力，保证系统动静态的跟踪能力；内环电流环控制最大电流，保证系统稳定运行。

图1 BLDCM控制系统simulink建模整体框图

运行仿真系统输出的三相反电动势波形如图2所示，三相定子电流波形如图3所示。二者均为梯形波，且较为理想，验证了系统建模的正确性。

图2 反电动势波形

图3 定子三相电流波形

3 BLDCM模糊控制系统

传统PID调控系统结构简单且控制效果较好，在工业自动化领域最先得到应用，但比例(proportion)、积分(integral)、微分(differential)参数一经确定在系统运行过程中就不能改变。在一些包含时变参数、非线性系统中PID调节很难达到预期的效果。模糊PID是基于模糊数学的高级控制，弥补了传统PID控制参数固定不变的不足，根据控制系统误差的变化，进行控制量自整定，其原理如图4所示。满足了实时更新PID参数的要求，很大程度上加强了控制系统的精确性和鲁棒性。

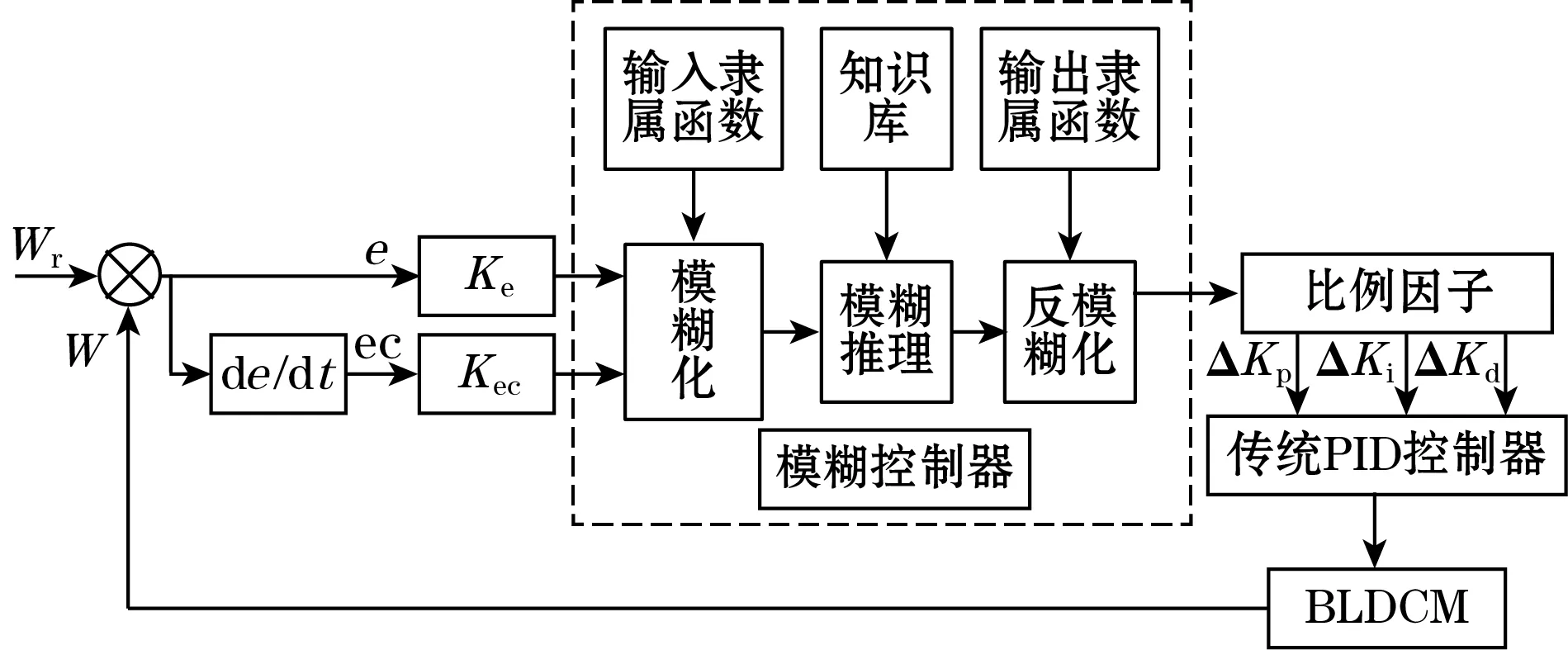
图4 模糊控制器结构框图

本文采用的是二维输入模糊控制器，其控制效果优于一维输入，三维输入模糊规则获取困难，计算复杂，不适合实时控制系统。根据输入误差e和误差变化率ec=de/dt，在模糊推理下输出PID参数修正值ΔKp、ΔKi、ΔKd，在线修正实际PID控制参数。

(4)

式中：Kp0、Ki0、Kd0为PID初始值。

3.1 模糊控制器设计

误差和误差变化率的论域为[-3,3]，输出变量ΔKp、ΔKi、ΔKd论域依次为[0,3]、[0,1]、[0,1]。输入输出变量的隶属函数形状选择三角形(trimf)，其运算简单，适合在线调整。反模糊化采用重心法，其本质是加权平均法，包含模糊集合所有信息，并依据隶属度大小有所侧重。e、ec、ΔKp、ΔKi、ΔKd的模糊语言变量均为{NB,NM,NS,ZO,PS,PM,PB}。模糊规则是模糊控制器的核心，应该满足完备性要求，规则的确定基于专家经验和学习算法。本文采用的模糊规则如表1所示。

表1 ΔKp、ΔKi、ΔKd的模糊控制规则控制表

4 基于飞蛾火焰算法(MFO)的模糊控制器优化

模糊控制器输入量e、ec经量化因子Ke、Kec量化后进入模糊控制器进行模糊推理，模糊控制器输出量经比例因子Kpp、Kii、Kdd比例运算后，输出ΔKp、ΔKi、ΔKd三个PID控制修正量。可见模糊控制的性能与量化因子和比例因子的关系甚大，Ke太大、Kec太小都容易造成系统产生超调，从而导致震荡不稳定。但是一般的模糊控制器创建完成后，这些参数是不能改变的，这大大影响到了系统的性能。根据上述不足，本文设计基于MFO算法优化的模糊控制器，控制功能框图如图5所示。

图5 MFO优化模糊控制的功能框图

4.1 飞蛾火焰优化算法

MFO算法诞生是受自然界飞蛾横向导航机制启发，通过飞蛾对火焰不断的螺旋收敛，在搜索空间中逐渐趋近最优解。螺旋搜索的方式使算法不易陷入局部最优，具有很好的全局寻优能力。

(5)

式中：M为飞蛾矩阵，每一行代表一只飞蛾；Mfit矩阵存储对应每只飞蛾的适应度值；i表示飞蛾的个数；j表示每只飞蛾的维度，即所代表的变量的个数。

对于火焰亦是如此，如下面矩阵所示：

(6)

式中：F是火焰矩阵，每一行代表一只火焰；Ffit矩阵存储对应每只火焰的适应度值；i表示火焰的个数；j表示每只火焰的维度。

F矩阵与M矩阵的不同之处在于更新方式，飞蛾是算法寻优过程中进行搜索的个体，而火焰是飞蛾在空间中搜索的最优位置，是飞蛾生成的标记。依据飞蛾的飞行轨迹建模，其位置更新机制可以用以下方程表示：

Mn=S(Mn,Fk)=Dnebtcos(2πt)+Fk

(7)

Dn=|Mn-Fk|

(8)

式中：Mn为第n只飞蛾；Fk为第k个火焰；Dn为第n只飞蛾与第k个火焰的距离；b为螺旋线的形状系数；t为 [-1,1]的随机数。

为加快MFO算法收敛速度，应自适应减少火焰的的数目，如式(6)所示：

(9)

式中：Nmax为初代火焰规模；n为当前迭代次数；T为最大迭代次数。

4.2 确定决策参数和评价标准

如图5所示，在控制系统中MFO算法对量化因子和比例因子进行寻优，所以每只飞蛾的维度为5，Ke、Kec取值范围设置为[1,3]，Kpp为[5,15]，Kii为[0.03,0.3]，Kdd为[0.01,0.1]。设置初代飞蛾种群大小为30，最大迭代次数为30。

适应度目标函数是确定火焰矩阵的重要标准，是MFO算法中的关键函数。在BLDCM控制系统中，依据快速性和准确性评价控制系统的好坏。超调量Mp，上升时间tr，调整时间ts，峰值时间tp是参考的指标，适应度函数确定如下：

fit=1/{αexp[-(Mp/Mp0)2]+βexp[-(tr/tr0)2]+

γexp[-(ts/ts0)2]+ηexp[-(tp/tp0)2]}

(10)

式中：Mp0=1%;tr0=0.2 s；ts0=0.2 s;tp0=0.2 s，是控制系统相应指标的期望值；α，β，γ，η是各个指标对应的权重系数，满足：α+β+γ+η=1。

本文α=0.5,β=0.1,γ=0.2,η=0.2。在进行适应度计算时，fit值越小证明系统性能越好。

本文还引入了同样可以评价控制系统性能的时间偏差绝对值积分型指标函数：

(11)

式中：e(t)=wr-w(t)为t时刻参考转速与实际转速的差值。

ITAE值越小则说明控制系统性能越好，本文利用ITAE函数验证fit适应度函数。

基于MFO算法的量化、比例因子寻优流程如图6所示。在进行适应度目标函数计算时，通过MATLAB中的assignin函数将算法中的飞蛾传入simulink仿真模型，通过sim函数运行仿真模型，计算出需要的评价指标。ITAE指标由simulink中的simout模块输出。

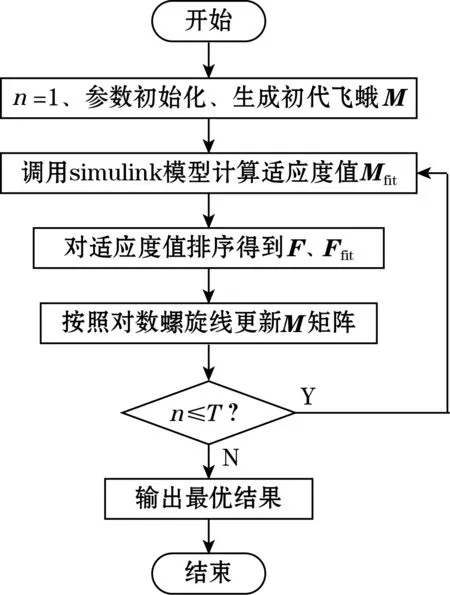
图6 MFO算法粒子寻优流程图

5 仿真结果与分析

本文设定无刷直流电机期望速度wr=800 r/min，仿真时间设置0.5 s，为使得结果分析更加精确，sim函数取样步长为0.000 1 s，设置传统PID控制和模糊PID控制作为对照组。运行3种BLDCM控制系统仿真模型，基于MFO优化后的模糊控制器量化因子和比例因子如表2所示，统计各评价指标如表3所示。由适应度目标函数值依次变小可知控制系统性能逐渐提升，由适应度目标函数的验证函数ITAE值亦可得出同样的结论，经MFO优化后的控制系统各项评价指标均很好的达到了期望值。图7是三种控制系统输出的转速曲线图。

表2 MFO优化后的量化因子和比例因子

表3 三种控制系统运行指标

图7 三种控制系统的转速曲线图

6 结论

本文提出了一种在线优化模糊控制器的新方法，设计了基于飞蛾火焰算法优化的模糊控制器，该算法具有优秀的寻优能力。文中建立了BLDCM仿真模型，编写了MFO算法的m文件，应用MATLAB/Simulink进行了仿真实验进行验证，结果显示其能够较好的实现无刷直流电机的速度控制，控制性能明显优于传统PID控制器和普通的模糊控制，具有较高的控制精度。