自具补偿互相关超声测距系统设计

朱义德,杨瑞峰,郭晨霞,葛双超

(中北大学电子测试技术国家重点实验室，山西太原 030051)

1 超声测距原理和互相关法测TOF

1.1 超声测距原理

超声波测量物体间距离的原理是基于脉冲回波法[1]，该方法利用声波的回波特性。如图1所示。

图1 超声波测距系统示意图

控制电路产生一个触发信号，这个信号由发射端T接收并受此激励产生超声波脉冲。脉冲传输至物体，遭遇物体阻拦时会产生脉冲回波，然后接收端R检测脉冲回波[2-4]。通过A/D转换器将发射端T的发射信号和接收端R检测信号分别作为参考信号和接收信号进行数字化，通过信号特征值(峰值、频率等)匹配计算出超声波的飞行时间(TOF)。最后结合飞行时长TTOF和所测的声速vU计算发射器T和接收器R到目标的距离L[5-7]。如式(1)所示。

(1)

1.2 互相关法测TOF

一般情况下，TOF是用阈值法计算的，但阈值法受信噪比的影响较大[8]。采用信号互相关算法，通过匹配发射信号与接收信号之间的相似度，从而识别出回波位置[9]。

互相关算法原理如下[10-11]：

用x(n)表示发射端离散时间信号，用y(n)表示接收端离散时间信号。

x(n)=z(n)+w1(n)

(2)

y(n)=z(n+τ)+w2(n)

(3)

式中：z(n)为超声波信号；w1(n)、w2(n)分别为发射端、接收端的干扰信号；τ为时间延迟序号。

将采集到的回波信号y(n)与发射信号x(n)进行N点的互相关运算,由于3个信号z(n)、w1(n)、w2(n)两两之间都互不相关，x(n)、y(n)的互相关表达式为

(4)

由式(4)计算出的Rxy(τ)表示回波信号y(n)与发射信号x(n)之间相似程度，互相关运算的最大值时刻即为时间延迟的估计值。

2 系统总体设计

系统采用cyclone四代EP4CE30F23V6N芯片为核心的FPGA，时钟主频为50 MHz，几十个I/O接口可以满足系统设计的要求。采用模块化方式设计系统，如图2所示。

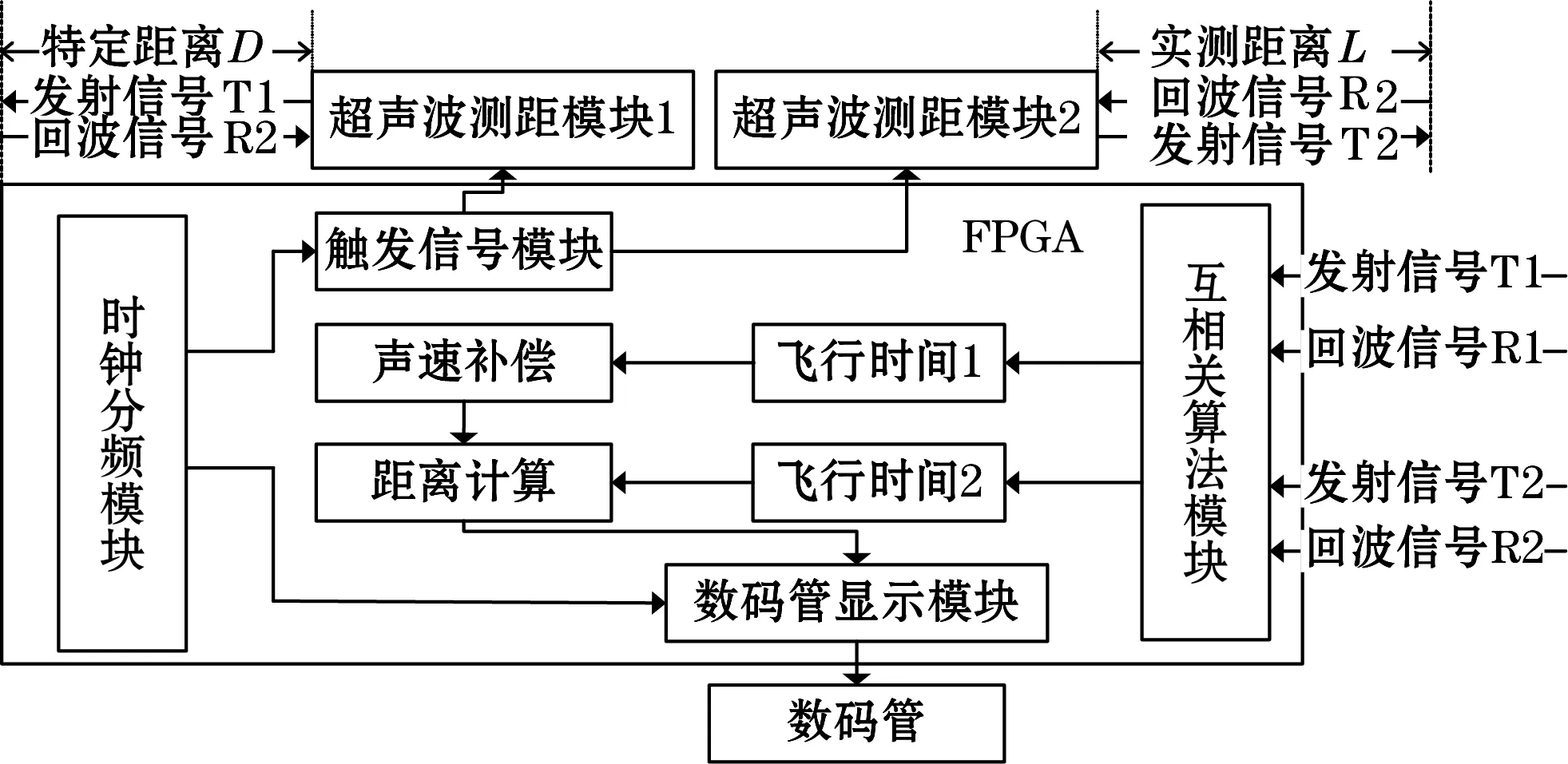
图2 系统总体设计框图

系统控制部分主要由时钟分频模块、触发信号模块、互相关算法模块、显示模块构成。分别完成时钟频率的调整、测距模块触发启动、TOF的测量以及测试距离的显示，其中的核心为互相关算法模块。为了降低测量误差，图中2个测距模块由相同测距装置组成。

在测距模块1中，已知特定距离D，经过互相关算法模块处理信号得出飞行时间TTOF1，由式(1)变换可得出实际声速，如式(5)所示：

(5)

再将vU代入式(1)中，得出精准的实际测试距离L。用第一组来测量声速作为第二组距离测量装置的补偿数据，这也是称之为自具补偿测距系统的原因。

3 测距模块设计

测距模块主要由2部分组成：一是产生超声波的脉冲发射电路，另一个是处理信号的回波接收电路。

3.1 超声波发射电路

超声波发射电路如图3所示，由功率放大电路、超声波脉冲生成电路组成。

图3 超声波发射电路

FPGA发出的PWN经过PNP型三极管放大和变压芯片升压，实现功率放大功能。变压芯片输出的放大脉冲会激励换能器生成超声波信号，由探头发出。

3.2 超声波接收电路

为了提高回波信号的信噪比，采用芯片CX2016A进行信号的放大、滤波、整形。超声波接收电路如图4所示。

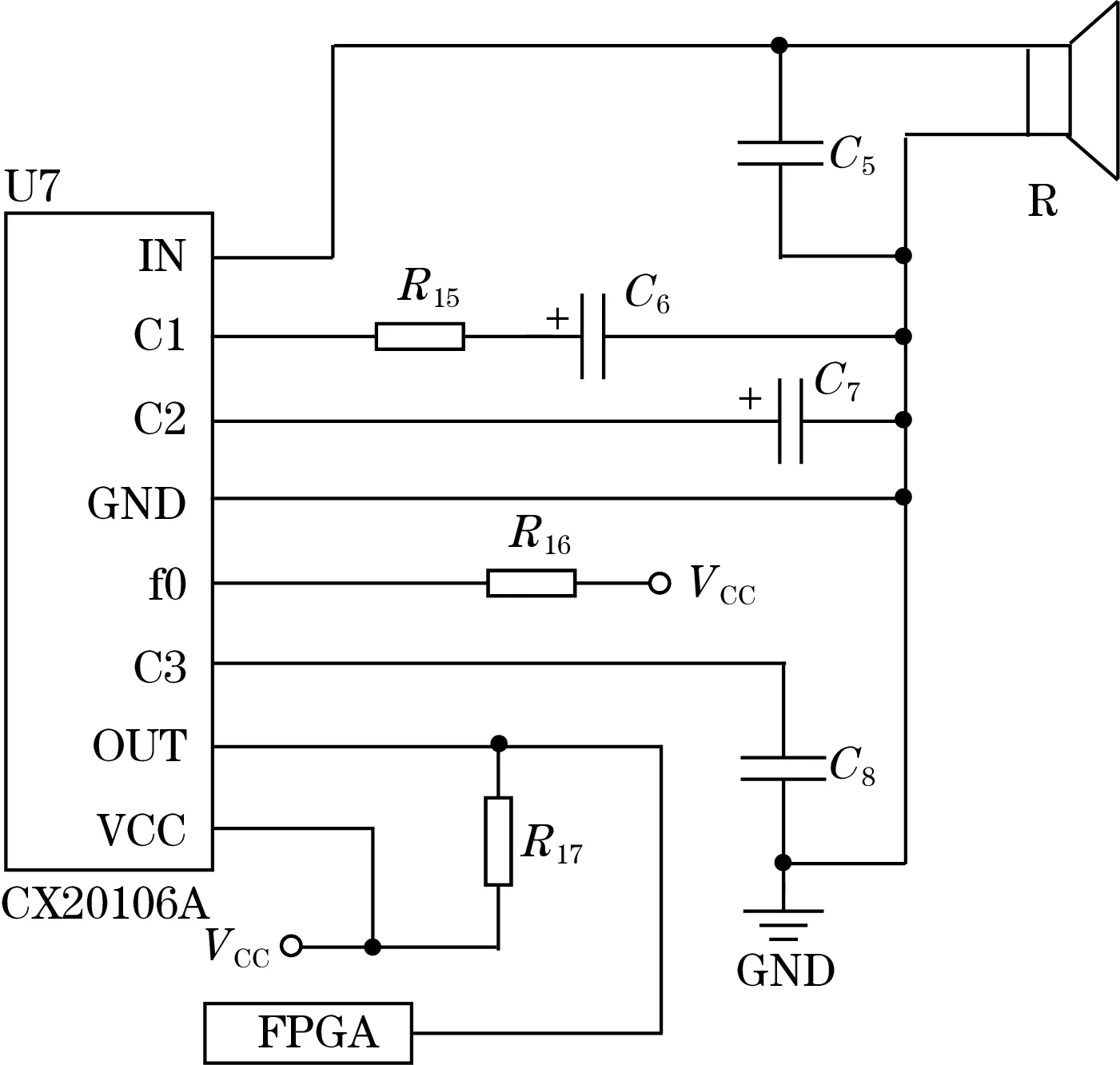
图4 超声波接收电路

图4中，VCC为+5 V。C1脚所连接的RC串联电路，R15和C6分别控制着芯片的前置放大增益和频率特性。C2脚上的电容C7为检波电容，影响电路的瞬时灵敏度。C3脚所连接电容为积分电容。通过改变各引脚上的器件的数值，可以调整回波接收电路，以满足设计的要求。

4 互相关算法模块

在式(4)中取z(n+τ)=g(n+τ)，可以得出一个卷积算式。如式(6)所示。

(6)

此处，*代表卷积。

4.1 半并行结构设计

只有在1个A/D采样周期内完成式(6)中的卷积运算，才能保证算法的精准实时性。卷积运算是2个变量在一定范围内相乘后求和的乘加结果，若是采用传统的并行方式在FPGA中实现式(6)中的运算，需要N个乘加器[12]。FPGA中的资源将被无意义使用，且电路和程序结构会被采样点数N的数值确定，修改过程繁琐并容易出错。为了增加算法的通用性和兼容性，能够灵活完成不同采样点数N的互相关运算，调整FPGA内部结构，采用半并行结构实现式(6)的算法，如图5所示。

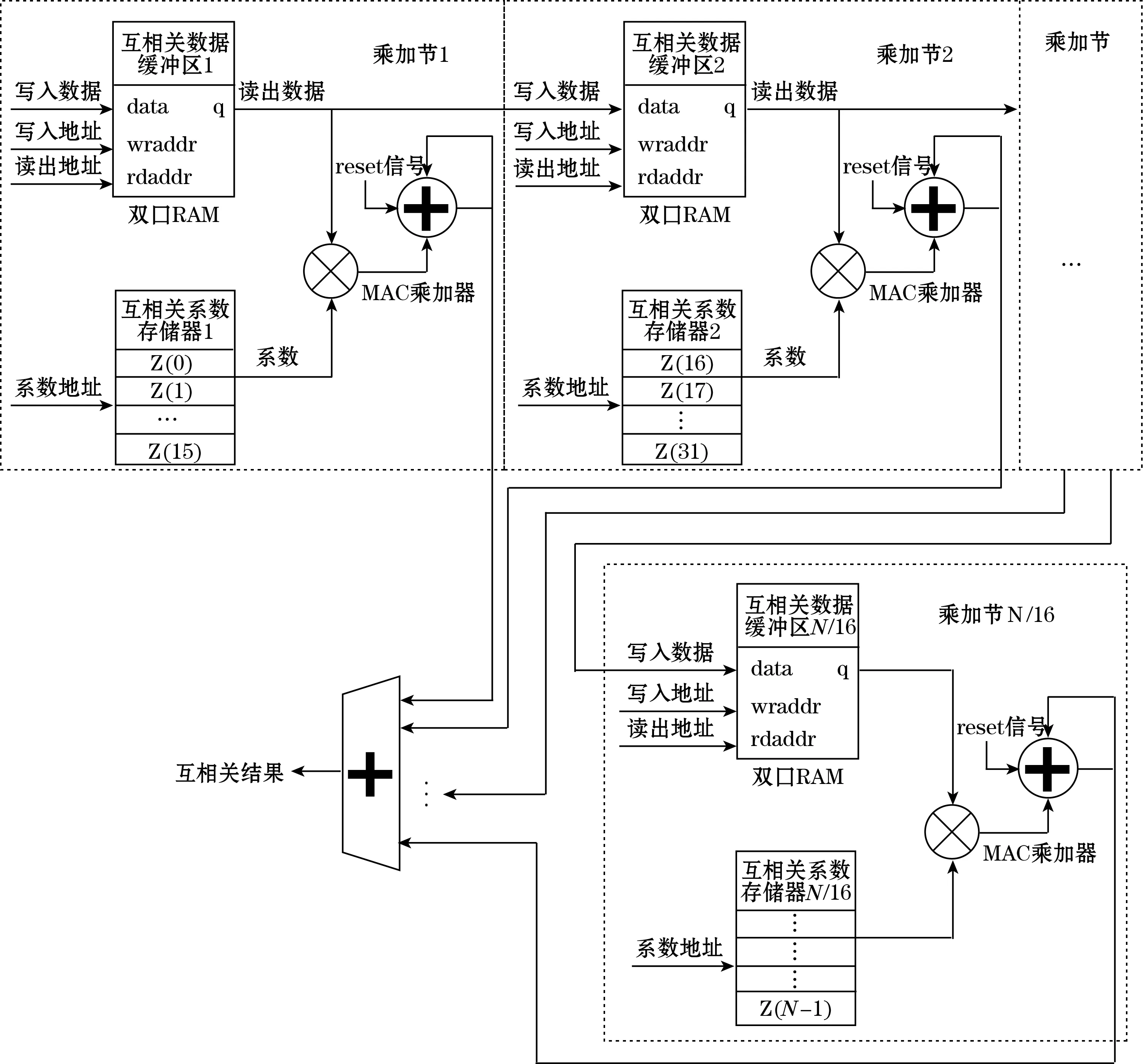
图5 半并行结构的互相关模块示意图

在设计互相关算法模块时，每个乘加节中的2个数据存储结构，应该满足以下要求：

在计算单个乘加节互相关Rxy(τ)时，互相关数据缓冲区中的输入数据g(n)以及互相关系数存储器中的互相关模板z(n)需要遍历。一个Rxy(τ)的计算完成后，乘加节会读出数据并被后一个乘加节写入。第一个乘加节会写入A/D采样得到的新缓数据，并将数据存储结构中最先写入的数据读出并写入下一个乘加节。最后一个乘加节只执行数据的写入和读取操作，“轮空”数据输出的功能。

假设采样点为64，采用图5中所示结构，只需要4个乘加节就可完成运算，降低了FPGA资源占用。还可以根据采样点数以及实际使用情况，灵活调整乘加节的数量。“缓冲存储”结构。图5中互相关系数存储器存入互相关模板z(n)后数据不更新。互相关数据缓冲区是存储写入数据g(n)的双端口RAM：一个负责在每个A/D采样周期中将1个新数据写入缓冲区，另一个用于读出数据，实现 “循环队列”数据读写结构。每个A/D采样周期中，2个存储器的数据会被按地址读取16次，读取出的数据在乘加器进行运算后输出进入加法器，得出互相关运算结果。

4.2 乘加节控制仿真

使用Quartus Ⅱ中的MegaWizard工具生成IP核，完成乘加节中的2个存储器双口RAM以乘加器模块设计，编写Verilog-HDL程序完成乘加节控制模块、顶层模块的的设计。由上文可知，整个互相关模块的重点是乘加节的实现。乘加节控制仿真波形如图6所示。

如图6所示，读取互相关系数存储器数据“coe_value”与互相关数据缓冲器数据“dp_rd_data”完成一次遍历乘加运算，被锁存器“s-latch”锁存。每段被写入采样数据进行乘加运算之前，现时数据地址“current_pt”会在触发指令“start”控制下完成加1操作。读数据缓冲地址寄存器/计数器“rd_data_dpram_add”会把“current_pt”作为原始数据写入。状态计数器“flag_cnt”的数值控制着双口RAM是否读出数据且在“flag_cnt=20”时停止地址计数，留出时钟周期作为双口RAM的地址潜伏期以及乘法器的潜伏期，实现16个数据的读取。

图6 乘加节控制仿真波形

5 实验结果对比

声波在空气中的速度，根据式(7)可以计算：

(7)

式中：γ、R、T和M分别为比热比、通用气体常数、绝对温度(单位：开尔文)和摩尔质量；声速c的单位为m/s。

综合考虑各个因素的影响，得出声速的实际应用算式。如式(8)所示。式中温度t的单位为℃。

(8)

由式(8)可知，影响声速的主要因素是温度。选择温度传感器作为温度补偿电路，替换超声测距模块1，修改程序进行控制，实现温度补偿。进行2组对比数据测试，一组是不使用互相关算法的温度补偿测距，一组是使用互相关算法的温度补偿测距。多次测量取平均值，进行数据对比。如表1所示。

表1 测距误差对比

根据表1中的数据得知，近距离测量误差较大，3种测试方式没有明显差别，这是因为超声波测距具有回波盲区。随着距离增大，测距精度差别明显。温度补偿测距没有使用互相关算法，测距误差一直在1%的范围内上下波动。自补相关测距精度高于温补相关测距精度，相对误差可以低至0.2%。测试距离超过150 cm后，测距的误差开始回升，这与超声波回波信号的衰减有关。

6 结论

针对超声波测距系统中硬件补偿电路补偿单一等问题，设计了一种基于互相关算法自具补偿的测距系统。在设计中，结合FPGA的功能特性，采用半并行结构简化互相关算法。测距系统中的声速补偿方法，不使用硬件补偿电路，而是基于空间环境条件进行声速补偿。与使用传感器完成环境数据测量后再进行反馈补偿的方式相比，该方法具有更好的环境适用性。使用相同的装置完成声速的补偿，既提高了测距的精度，又减少了工作量，同时降低程序的出错率。系统可在线拓展升级，有实用价值。