某机载雷达机箱焊缝结构疲劳仿真及试验研究

刘家华，邢嘉路，张梁娟，李齐兵

(南京电子技术研究所，江苏 南京 210039)

机载雷达机箱作为机载雷达的重要部件，集成了雷达射频、信号处理、供电等多种重要功能，其结构可靠性对于雷达整机性能具有关键影响。机载环境由于载机发动机结构形式及运行条件不可避免地产生了严苛的振动冲击环境条件，对于舱内雷达机箱而言，随机振动已经成为影响设备结构可靠性的关键环境因素[1-2]。随着数字化设计仿真技术的发展，雷达设备结构可靠性已逐渐由经验设计发展为数字化仿真设计，国内外相关学者已对该问题进行了大量研究。

目前针对机载雷达设备动力学可靠性的研究主要集中在对设备结构应力仿真结果最大点的校核，试验主要以耐久振动验证为主，缺少对机箱关键位置的动力学响应测试及与仿真结果的对比分析。机载雷达机箱结构一般采用焊接成型，焊缝位置的应力值虽然可能并非是全局最大，但由于其焊接缺陷不可避免、焊缝易发生疲劳断裂等特点，焊缝处往往会成为整个设备结构的薄弱环节[3]。对于液冷机箱，液冷流道位置焊缝失效可能引起冷却液泄漏，最终导致电子设备失效，从而影响雷达工作甚至飞机飞行安全，因此有必要对机载雷达设备焊缝结构疲劳问题进行研究。本文针对某型机载雷达机箱，提出了机箱焊缝结构的动力学响应分析方法，通过数值计算研究了机箱焊缝位置在随机振动载荷下的响应，再通过试验对焊缝多个关键点应力值响应进行测试，并与数值计算结果进行比较，验证了机箱焊缝位置仿真结果的可靠性。

1 机载雷达机箱焊缝结构疲劳分析方法

1.1 随机振动响应分析

随机振动作为一种不确定的振动，其规律无法直接用确定的函数描述，一般用概率统计方法来描述其随机过程。根据随机过程理论，对于稳态随机过程可用功率谱密度函数对其频域响应进行描述，其表征了随机过程在各频率能量分布的情况[4]。自功率谱密度函数Sx(f)可由自相关函数进行傅里叶变换得到：

(1)

式中：Rx(τ)为时域随机信号；j为虚数单位；f为频率；τ为延迟时间。

实际问题中只考虑非负频率域，因此单边自功率谱密度函数Gx(f)可表示为:

Gx(f)=2Sx(f)f≥0

(2)

对于多自由度系统，其动力学方程可表示为：

(3)

(4)

Sy(ω)=H*(ω)Sx(ω)H(ω)

(5)

式中：H(ω)为系统的频率响应矩阵；H*(ω)为H(ω)复共轭矩阵。

1.2 疲劳寿命分析方法

目前在随机振动条件下常用的疲劳寿命分析方法主要分为频域法和时域法[4]，本文采用基于功率谱密度的频域法进行分析。基于功率谱密度的疲劳寿命预测方法主要有Dirlik模型、Wirsehing模型、Rice模型、Bendat模型等[5]，其计算过程较为复杂，计算量大，不适合用于工程实际中复杂结构的疲劳寿命评估，因此本文采用Steinberg提出的三区间模型对疲劳寿命进行估计[6]。

由Miner线性损伤理论可得，对于n个应力载荷引起的疲劳损伤累计(即总疲劳损伤)D为：

(6)

式中：Di为第i个载荷引起的疲劳损伤；ni为第i个载荷引起的循环次数；Ni为结构在第i个载荷作用下破坏的循环次数。

当n个应力载荷引起的总疲劳损伤D=1时，认为结构发生破坏。Steinberg提出由于结构随机振动应力一般服从高斯分布，因此结构产生3σ应力的概率为99.73%，应力幅值在3σ应力范围外的占比很小，假定其对结构不产生疲劳损伤。将3σ范围内应力分为[-σ,+σ]、[-2σ,-σ)∪(+σ,+2σ]、[-3σ,-2σ)∪(+2σ,+3σ] 3个区间，应力分布于以上3个区间的概率分别为68.30%、27.10%、4.33%。结合Miner理论可得由3个区间应力引起的疲劳损伤为：

(7)

式中：nσ,n2σ,n3σ分别表示应力范围为[-σ,+σ]、[-2σ,-σ)∪(+σ,+2σ]、[-3σ,-2σ)∪(+2σ,+3σ]的实际循环次数；Nσ,N2σ,N3σ分别为该应力值对应的疲劳损伤循环次数。

对于高斯随机过程，预期的单位时间内应力循环数f+可通过式(8)进行计算[7]：

(8)

式中：m2和m0分别为2阶和0阶中心矩。n阶中心矩mn定义如下：

(9)

式中：G(f)为频率f处的单边功率谱密度函数。

材料S-N曲线可表达为：

SmNS=C

(10)

其中：S为应力值；NS为应力值为S时的疲劳应力循环次数；m,C为材料相关常量。因此结构在时间Tf内总疲劳损伤为：

(11)

当D<1时认为结构在该时间内不会发生疲劳破坏。

1.3 机载雷达机箱焊缝随机振动疲劳寿命评估方法

机载雷达设备大量采用焊接成型，在随机振动条件下焊缝的可靠性对设备结构可靠性具有重要影响。由于焊缝具有易发生疲劳失效的特点，焊缝位置应力值虽然可能并非全局最大，但焊缝处疲劳强度一般低于母材，因此必须对焊缝位置的疲劳寿命进行校核。本文结合随机振动响应及疲劳寿命计算方法，提出机载雷达设备焊缝随机振动可靠性评估方法如下：1)根据机箱结构及其焊接方法，建立包含焊缝的有限元模型；2)通过有限元方法求解机箱模态及随机振动响应，获得焊缝位置应力响应，找到焊缝位置应力最大点；3)根据焊缝位置随机振动应力响应，采用三区间法计算焊缝疲劳寿命；4)通过对设备进行随机振动试验，对比试验开始及结束时关键焊缝位置应力变化情况，验证设备焊缝结构可靠性。

2 机载雷达机箱焊缝结构可靠性仿真分析

2.1 机箱焊接结构介绍

机载雷达机箱作为电子设备载体，集成了信号处理、数据处理、射频综合等功能。目前机载雷达机箱大部分采用风冷或液冷方式进行电子设备冷却，液冷机箱冷却能力强，广泛用于大功率机载雷达机箱结构中，因此本文选择液冷机箱进行研究。某典型雷达机箱结构如图1所示，机箱通过前面3个螺钉和后面2个定位销套与飞机连接。由于箱体内部结构复杂，无法通过机加工直接成型，需要通过冷板焊接、冷板机加工、机箱焊接、机箱机加工、机箱装配以及电装等多道复杂工艺才能完成。焊缝结构可靠性直接影响雷达整机可靠性，因此需要对焊缝结构可靠性进行分析。

图1 某机载机箱焊接结构

2.2 设备有限元模型建立

本文采用ANSYS Workbench软件对某典型机载雷达机箱进行有限元分析，机箱结构如图2所示，主要由机箱箱体及内部模块组成，箱体采用铝合金焊接成型。由于原设备结构较为复杂，需对其结构进行简化，同时将设备内部模块采用等厚实心块代替，并对模块进行质量等效。焊缝位置采用网格共节点处理。箱体与模块均采用高阶四面体及六面体实体单元进行网格划分，单元数为239 693个，节点数为533 030个。箱体及模块材料均为铝合金5A06(H112)，其弹性模量为70 GPa，泊松比为0.33，抗拉强度为295 MPa，屈服强度为135 MPa。

图2 某机载雷达机箱结构及有限元模型

2.3 模态分析

对机箱进行模态分析，得到其在载荷频率范围内的固有频率及振型。机箱前10阶模态固有频率见表1。前10阶模态的质量参与系数之和大于90%，因此取前10阶模态足以保证仿真的准确性。前3阶模态振型如图3所示。

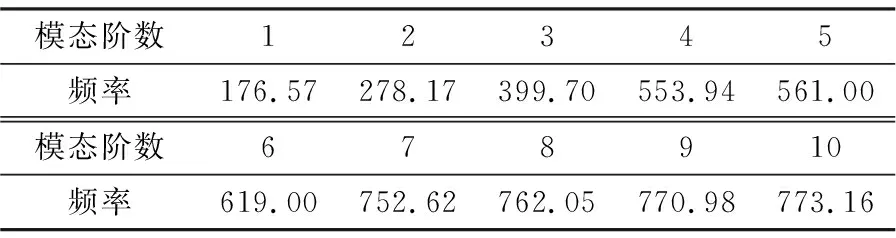
表1 模态分析结果 单位：Hz

2.4 随机振动分析

随机振动分析是以模态分析为基础，采用模态叠加法进行计算。机箱随机振动输入PSD(power spectrum density，功率谱密度 )曲线为设备安装的载机环境条件，如图4所示，耐久振动时长Tf=3 h。对机箱施加Z方向随机振动载荷，材料阻尼比设置为0.03，求解得到机箱随机振动应力响应，其3σ应力分布云图如图5所示，可以看出设备全局应力最大点出现在后支耳根部，本文重点对焊缝位置应力进行研究。

图3 机箱前3阶模态振型

图4 随机振动输入条件

图5 随机振动应力分布

提取4条焊缝位置的随机振动应力分布(焊缝位置如图6所示)，输出4条焊缝上节点沿焊缝路径3σ应力值分布曲线(如图7所示)，路径方向为从前面板到后面板，横坐标为节点位置在路径上的百分比。从图7中可以看出,焊缝2、焊缝3应力水平高于焊缝1、焊缝4，同时靠近后面板处焊缝应力明显升高。最大应力出现在焊缝2靠近后面板处，应力值为20.9 MPa。焊缝2最大应力点处的应力在Y,Z方向分量PSD曲线如图8所示，可以看出2个方向应力功率谱峰值均出现在频率176 Hz附近，结合模态分析结果可知，焊缝最大应力响应主要来自于1阶固有频率处发生的共振。

图6 箱体焊缝位置

图7 不同焊缝位置应力分布

图8 焊缝最大应力点Y,Z向应力分量响应PSD曲线

2.5 焊缝疲劳分析

根据焊缝处随机振动分析结果，对焊缝位置进行疲劳分析。由随机振动计算结果可得，焊缝位置最大应力点的3σ应力值为20.9 MPa。根据文献[8]中5A06铝合金焊缝疲劳极限41.80 MPa及S-N曲线，对机箱焊缝最大应力位置进行疲劳寿命分析。根据该点应力响应可得：1σ应力对应S-N曲线循环次数Nσ=∞；2σ应力对应S-N曲线循环次数N2σ=∞；3σ应力对应S-N曲线循环次数N3σ=∞。

由图7中焊缝位置应力响应PSD曲线及式(8)可得，预期单位时间内应力循环数f+为：

式中m2和m0通过随机振动得到的Z向焊缝最大应力点PSD计算得到。因此由式(11)可以得到结构在时间Tf内总疲劳累计损伤为：

由以上结果可知该机箱焊缝强度能够满足耐久振动要求，无疲劳破坏风险。

3 焊缝随机振动试验研究

为了对上述仿真计算结果进行验证，同时探究焊缝位置实际振动过程中的应力响应，本文对该机载机箱进行随机振动耐久试验，耐久振动条件如图4所示，振动时间为X，Y，Z3方向各40 h，累计120 h振动时间等效雷达全寿命周期工作情况。在振动过程中，采用动态应变仪对机箱关键焊点位置进行应力采集，根据仿真结果，共设置4个测点，测点粘贴位置如图9所示。本文主要以焊缝最大应力处Z向为例进行分析。

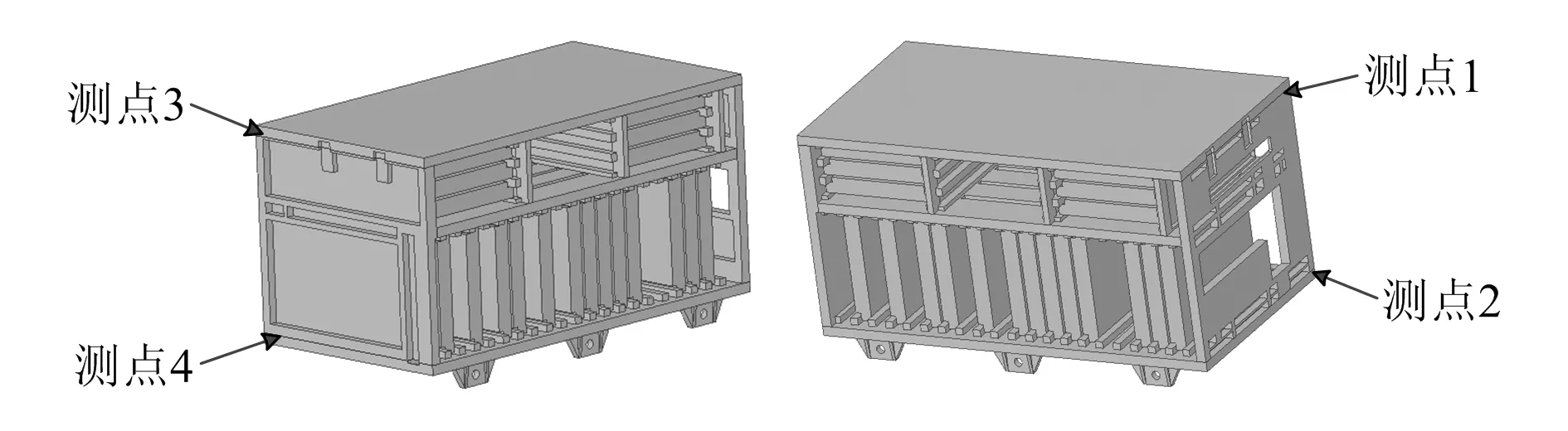
图9 应力采集测点位置

按图4给出的环境条件输入随机振动载荷，进行Z方向40 h随机振动试验并采集各测点应变值，采集时间为10 min。测点采用直角应变花对焊缝处YZ平面的应力状态进行测量，采样频率为5 000 Hz，得到应变值后按式(12)～式(14)对各向应力进行计算：

(12)

(13)

(14)

式中：σy和σz分别为平面Y,Z方向应力值；E为材料弹性模量；μ为泊松比；εy和εz为Y,Z方向应变值；ε45°为45°方向应变值；τyz为YZ平面内切应变值。

由各向应力计算得到各测点时域内Von Mises应力值，如图10所示，为保证结果精度需剔除3σ范围外的应力值。将各测点Von Mises峰值应力与仿真测点位置峰值应力结果进行对比，见表2，可以看出测点2、测点4应力高于测点1、测点3峰值应力，最大应力出现在测点2位置，该位置为焊缝2靠近后面板位置处，与仿真结果一致。同时试验与仿真峰值应力值基本符合，表明仿真结果能够一定程度上反映焊缝真实受力情况。

图10 测点2时域Von Mises应力

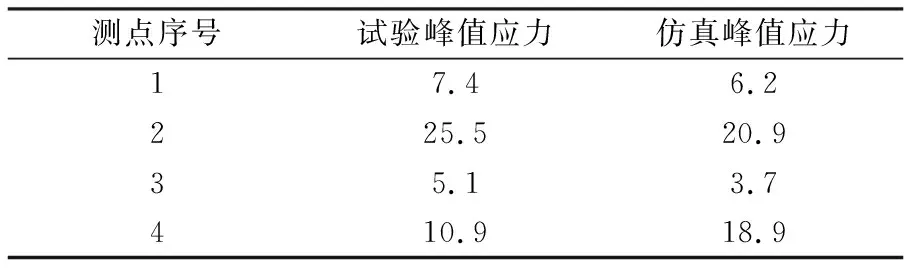
表2 各测点峰值应力值 单位：MPa

为反映焊缝位置应力在频域内的响应，将采集得到的时域应力信号进行处理得到焊缝位置应力PSD响应。本文采用Welch法对时域应力信号进行功率谱估计。由于篇幅限制，以测点2Y向应力分量响应为例进行说明。测点2Y向应力分量PSD曲线如图11所示，PSD峰值响应出现在148 Hz附近，该频率值与仿真结果1阶模态频率较为接近，可以认为1阶模态共振是造成峰值应力响应的主要原因。

图11 测点2 Y向分应力PSD响应

由图可以看出,试验值PSD峰值响应频率点与仿真值较为接近，两条曲线整体趋势基本一致；计算得到试验值PSD总均方根值为2.98 MPa，仿真值为2.76 MPa，仿真与试验结果能够较好吻合，仿真结果较为可靠。

由于文中式(11)是基于应力分布为高斯分布的疲劳寿命估计方法，因此有必要对雷达设备焊缝位置应力的概率密度分布进行研究，判断其是否符合高斯分布。对测点2Y向应力值进行统计，得到其概率分布图并进行高斯分布拟合，如图12所示。可以看出Y向应力值分布规律能够较好地符合均值为1.36、标准差为2.96的高斯分布，因此能够满足Steinberg提出的三区间疲劳寿命计算方法条件。测点2 Von Mises应力均值为7.8 MPa，标准差为5.9 MPa，因此该点1σ应力值为13.7 MPa，2σ应力值为19.6 MPa，3σ应力值为25.5 MPa，由实测应力循环得到单位时间内应力循环数f+=249.0 Hz，因此由式(11)可知焊缝疲劳寿命能够满足要求，与2.4节分析结果一致。

图12 测点2 Y向分应力概率密度分布

累计完成Z向40 h随机振动试验后目测结构焊缝处无明显损伤。采集设备最后10 min试验焊缝位置应变，按上述方法对其数据进行处理得到测点处应力，与试验开始前10 min试验结果进行对比。以测点2为例，其Y向应力PSD响应如图13(a)所示。经过40 h随机振动试验后，测点2处最后10 min该处Y向应力PSD响应如图13(b)所示。可以看出试验前后测点2处PSD变化较小，该处应力响应未发生明显变化。以该方法对X,Y向40 h振动试验前后应力进行分析，结果与Z向一致，应力响应未发生明显变化，因此可以认为经过120 h随机振动后机箱焊缝结构未发生明显变化，该机箱成功通过耐久振动试验，证明机箱焊缝可靠性能够满足雷达全寿命周期工作要求。

4 结束语

本文针对机载雷达机箱焊缝在随机振动条件下可靠性问题，提出了机载雷达机箱焊缝可靠性分析方法，结合仿真及试验分析得到了典型机箱焊缝位置的动力学响应，并对焊缝危险点疲劳寿命进行了评估。可以看出本文方法能够有效评估典型机载雷达机箱焊缝可靠性，该方法较传统焊缝疲劳预测方法计算简单，更适用于工程实际；同时仿真结果在峰值应力及频域响应上均能较好地符合试验结果，具有一定可靠性。该方法为机载产品焊接机箱设计制造提供了依据，具有较强的工程指导价值。

图13 测点240 h试验前后Y向分应力PSD响应