数学形态学下的多尺度灰度图像增强应用分析
2021-05-18谢瑾
谢 瑾
(兰州大学数学与统计学院,甘肃 兰州 730100)
数学形态学在图像处理方面的基本原理是将图像当做一个集合,以某种形状的结构因子与图像加以求补、移位、交、并的集合运算,不同的集合运算形成了不同形态的数学运算结果[1-2]。数学形态学在图像处理中可以分为二值数学形态学和灰度数学形态学,二值数学形态学处理图像的原理是数学集合的交与并的运算,而灰度数学形态学主要关注极大值与极小值的运算。
1 灰度数学形态学在图像运算中的腐蚀与膨胀
假设原灰度图像为 f(x,y),结构元素为 b(x,y),其中整数集合为 Z,另设 (x,y)为 Z×Z 中的元素,则 f(x,y),b(x,y)分别为图像及结构元素位于(x,y)的灰度值。
定义 1结构元素 b(x,y)对原灰度图像 f(x,y)的形态学腐蚀用f⊗b 表示为

式中:Df与Db分别表示 f(x,y),b(x,y)的定义域。
所谓腐蚀,即腐蚀变换,指的是在结构元素确定的邻域块中选取图像值和结构元素值进行减运算得到的最小值。
定义 2将结构元素 b(x,y)对原灰度图像 f(x,y)的数学形态学膨胀描述用f⊙b 表示为


式中:Df与Db分别表示 f(x,y),b(x,y)的定义域。
根据腐蚀的含义,腐蚀变换是在结构元素确定的邻域块中选取图像值和结构元素值进行减运算得到的最大值。灰度图像的腐蚀与膨胀变换对比,见图1。

图1 灰度图像的腐蚀与膨胀变换对比图
选取3×3 的结构元素,对原灰度图像分别进行腐蚀和膨胀运算,从图1-b 能够明显得到腐蚀变换加深了图像整体暗度的结论,同时使图像的边缘更加细腻;从图1-c 能够得到膨胀变换对图像处理结果与腐蚀变换相反的结论[3-4]。
2 对多尺度灰度图像增强算法分析
灰度数学形态学变换的原理,即从原输入图像中所得的差进行开运算,得到的图像能够表现出某些明显的特征,本文根据所选图像将此变换定义为Lady-Hat (LH)增强变换,可以表示为

式中:b表示结构元素;f表示原输入图像。进行开运算的目的是尽量过滤掉小于结构元素尺寸的高亮部分。利用式 (3)获取图像中的峰值信号,因此也可以把式 (3)叫做亮Lady-Hat (HLH)增强变换,主要作用是可以获取图像中小于结构元素尺寸的亮特征。除此之外,还可将式 (3)定义算子的对偶算子表示为

闭运算可以过滤掉小于结构元素尺寸的灰暗点,利用式 (4)获取图像中的波谷信号,把式(4)叫做暗Lady-Hat (LLH)增强变换,主要作用是可以获取图像中小于结构元素尺寸的暗特征。
Bai X Z 等[5]将多尺度分析应用于图像的锐化增强处理中,采用的思路是先选择特定形态的结构元素基于Lady-Hat 增强变换提取图像中的亮、暗详细特征,分别对亮、暗详细特征进行增强运算,再将分开得到的结果结合,重新构成符合原灰度图像结构的增强图像,其运算原理表示为

式中:g 为增强变换之后的最终图像;f 为原输入图像;i 为尺度。这种图像增强变换方式会对图像产生增强效果,但是考虑到结构元素的尺度以及灰度图像的多尺度问题,仍可以对算法进行优化。在灰度数学形态学的变换中,在结构元素的选择上如果尺度过小,在图像的变换中可能产生多余噪声;相对应的,如果尺度过大,又会导致在图像变换中必要细节的缺失,边缘变得模糊。避免以上问题的关键在于结构元素的尺度选择要合理,选择多尺度的结构元素可以有效地解决以上问题,多尺度结构元素可以表示为

式中:b0表示小尺度结构元素;n 表示膨胀次数。则较大尺度的结构元素可以由小尺度的结构元素经过(n-1)次膨胀获取。把多尺度的思路应用到Lady-Hat 增强变换中去,于是获取了多尺度Lady-Hat 增强变换算法。HLH 增强变换的表达式为
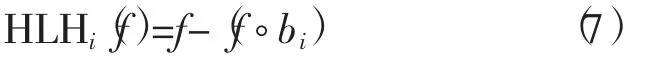
LLH 增强变换的表达式为

根据式 (7)和式 (8)能够获取原输入图像不同尺度下的亮部与暗部的详细特征。图2 为示例图像的多尺度Lady-Hat 增强变换下获取的详细特征。

图2 多尺度增强变换详细特征对比图
随着尺度i 数值的增大,结构元素的尺寸随之增加,从得到图像的结果能够看出获取到的小尺度的图像细节特征逐渐增多,冗余也越来越明显。如果能够得到不同尺度下的有效细节特征,进而提出冗余得到优化的细节特征[6],提炼算法表示为

图3 为根据式 (9)和式 (10)为示例图像的多尺度Lady-Hat 无冗余下获取的详细特征。
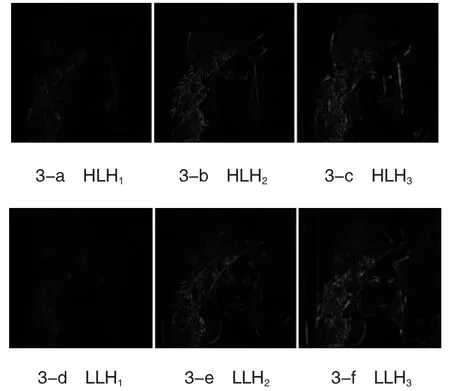
图3 多尺度无冗余详细特征对比图
在最大尺度为n 时可以按照式 (9)和式 (10)对原灰度图像做Lady-Hat 增强变换,同时获取多尺度的有效亮部和暗部的详细特征,具体表示为
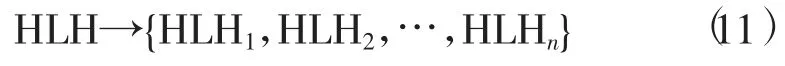

在获取原灰度图像的亮部及暗部详细信息后就可以对图像进行重构计算,达到图像增强的目的。图像的详细特征载体主要是像素以及其区域背景的对比度,要想实现图像的增强,要对图像的亮部和暗部细节以相同的比重构建[7],在本算法中主要体现在相同尺度下二者选取相同的权值,将本文所用的多尺度Lady-Hat 增强变换的最终算法表示为

式 (13)中的权值λi决定了图像转换后亮部与暗部详细信息的比例,通常取值为[1/2,1],实际比例会因为各个尺度的变换而变化。因此,在运算中需同时考虑尺度i 和权值λi。在现实生活中,人的视觉往往在多尺度范围较小的Lady-Hat 增强变换获取的细节中表现出显著的敏感性,那么就需要在图像的增强运算中,为小尺度的Lady-Hat 增强变换赋予相对较大的权值,为大尺度的Lady-Hat 增强变换赋予相对较小的权值,于是可以用λi表示尺度为i 的权值,表示为

得到尺度i 与权值λi的对应数据表,见表1。

表1 尺度与权值取值的对应表
多尺度灰度图像优化算法下的图像转换效果见图4,可以看出经过多尺度优化后的算法对图像进行转换,亮、暗显著优于简单尺度的增强效果。

图4 多尺度优化算法下的Lady-Hat 图像转换效果对比图
3 结束语
多尺度灰度图像的增强算法是基于灰度数学形态学的基本原理,通过仿真实验发现,多尺度灰度图像的细节增强方法使得增强后的图像细节突出、信息含量增加,图像综合质量明显好转,但是仍存在部分亮、暗细节模糊的问题,值得对模糊原因及清除方法进行更深入地研究。
