关于非局部扩散模型的一种快速预处理算法
2021-05-18冉育红李存吉殷俊锋
冉育红,李存吉,殷俊锋
(1. 西北大学数学学院,陕西西安710127;2. 西北大学数学学院,陕西西安710127;3. 同济大学数学学院,上海200092)
对于自然界那些用整数阶扩散方程不太好描述的现象,如反常扩散和多孔介质流等[1−3],除了可以用分数阶扩散方程建模以外,非局部扩散模型也是一种可供选择的建模方法。非局部扩散理论对间断性问题及其他连续体变形问题给出了一个恰当的描述,而裂缝、断裂等奇异性问题在经典理论方程下无法给出恰当描述。非局部理论被引入到连续介质力学当中,2000 年Silling 提出了一种叫做peridynamic的非局部扩散模型[4−7],在非局部扩散模型框架下,物体内部不再有接触力,并且可以保证建立的方程都保持同一积分形式,对间断或其他奇异性连续体的变形问题提供了新的研究思路。
然而,利用一般的数值方法数值离散非局部扩散模型,通常得到一个稠密的刚度矩阵,利用直接法求解的计算量和存储量非常大,从而阻碍了其广泛应用。最近Wang C 等提出了一种快速的配置法数值离散变系数非局部扩散模型[8],分析了刚度矩阵的结构,并利用直接法和共轭梯度平方法求解了变系数非局部扩散模型经过快速配置方法数值离散得到的线性方程组。因为直接法的计算量太大,共轭梯度平方法不稳定,所以这两个方法不实用。
由于变系数非局部扩散模型经过快速配置方法数值离散得到的线性方程组系数矩阵为非对称的,因此可以用间接法中的GMRES 方法[9]求解。在实际求解过程中,系数矩阵的坏条件数会导致GMRES方法收敛的很慢甚至不收敛,而提高收敛速度最常用的方法是预处理技术[10−13]。一个好的预处理子应该至少保持某种特殊结构,并使得预处理后的系数矩阵的条件数很小。在文献[8]的研究基础上,本文采用了Toeplitz 及循环预处理GMRES 方法求解了变系数非局部扩散模型经过快速配置方法数值离散得到的线性方程组。
1 问题的来源
本节给出了所需要求解的线性方程组,即变系数非局部扩散模型经过快速配置法数值离散后所得到的离散方程。
1.1 非局部扩散模型及其快速配置法
变系数非局部扩散模型的一类体积约束非局部Dirichlet边值问题,可以表示如下[5]:
式中:δ >0表示非局部扩散现象扩散的水平方向的范围;α(⋅)用来表示可变的扩散系数,并假设其有正的上下界且光滑。核被定义为



1.2 刚度矩阵的元素估计



1.3 刚度矩阵的结构分析
从参考文献[8]可知,刚度矩阵A可以分解为


2 预处理GMRES算法
本文利用快速配置法数值求解变系数非局部扩散模型最终归结为线性方程组式(6)的求解,其中系数矩阵A由式(18)所定义,右端项f由式(7)所定义。由于系数矩阵A 为非对称矩阵,所以可以利用GMRES 方法求解线性方程组式(6)。为了提高GMRES 方法的收敛率,本节构造了系数矩阵A 的Toeplitz 及循环预处理子,提出了预处理GMRES 算法。首先,本文给出几个基本定义:



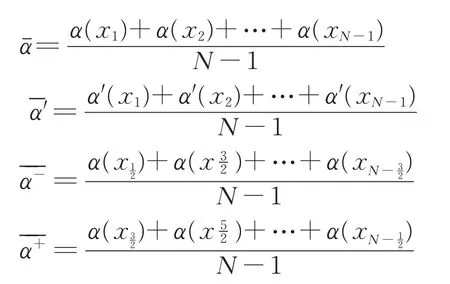
由于P1为Toeplitz矩阵,在PGMRES算法中,求解以P1为系数矩阵的残量方程P1z=r的计算量太大。为减少计算量,我们进一步用P1的Strang 循环近似矩阵逼近P1,令C为Toeplitz 矩阵T的Strang 循环逼近矩阵,即T≈C,则得到刚度矩阵A的如下预处理子

由于预处理子P2为循环矩阵,则P2可以通过离散的傅里叶变换进行对角化P2=F*ΛFn,所以只需要一次FFT 和一次逆FFT 变换可求出,PGMRES算法中残量方程P2z=r的解z=F*Λ−1Fn r,计算量仅为O(NlogN).
同时,在以上PGMRES 算法中还涉及到Toeplitz 矩阵与向量相乘,由于Toeplitz 矩阵与向量的乘积可以嵌入到2(N- 1) ×2(N- 1)阶循环矩阵与向量相乘中,也可以通过FFT计算量得到,计算量仍是O(NlogN),所以PGMRES 算法每次迭代的计算量为O(NlogN)[17−18]。
3 数值算例
通过数值实验来验证本文构造的刚度矩阵A的循环预处理子P2的有效性,分别利用GMRES方法、预处理GMRES 方法求解线性方程组式(6),其中系数矩阵和右端项分别由式(18)和式(7)定义。所有迭代法都以零向量作为初始向量,迭代终止条件为

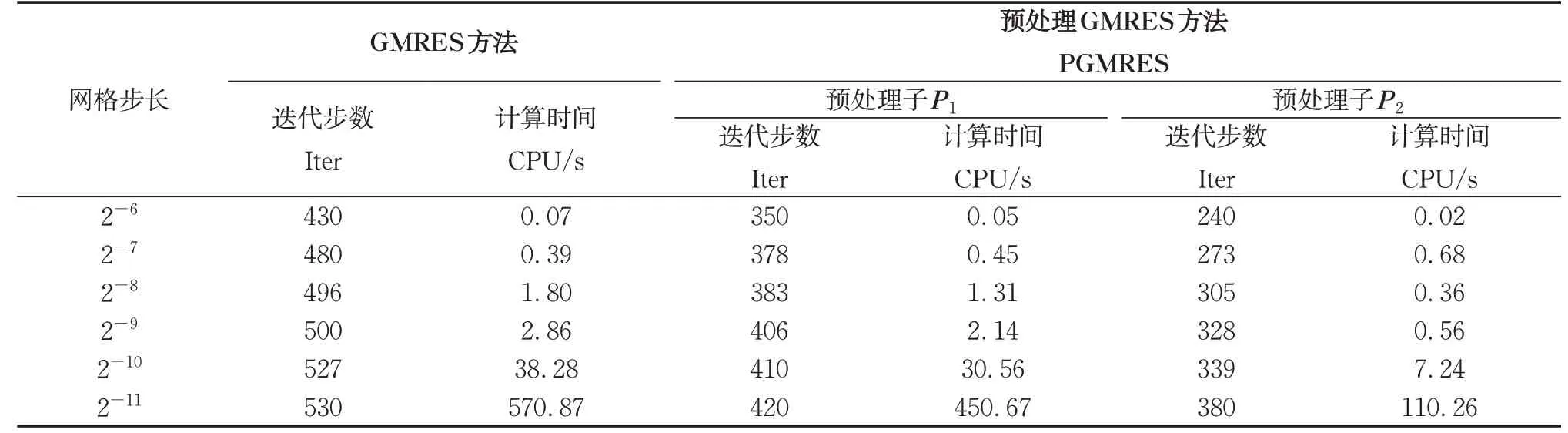
表1 算例1的数值结果Tab.1 The numerical results for Example 1
从表1和表2可以得出以下结论:三种算法算出来的数值近似解是相同的;预处理GMRES算法需要的迭代步数和计算时间比GMRES 算法需要的迭代步数和计算时间少;P2做预处理子时需要的计算时间在这三种算法中是最短的。
图1 和图2 当中的横坐标表示矩阵特征值的实部,纵坐标表示特征值的虚部。从这两个图中,发现预处理矩阵的特征值分布比原始矩阵的特征值分布集中,说明预处理矩阵的条件数比原始矩阵的条件数小,故预处理GMRES方法的迭代步数比GMRES方法的迭代步数少。

表2 算例2的数值结果Tab.2 The numerical results for Example 2
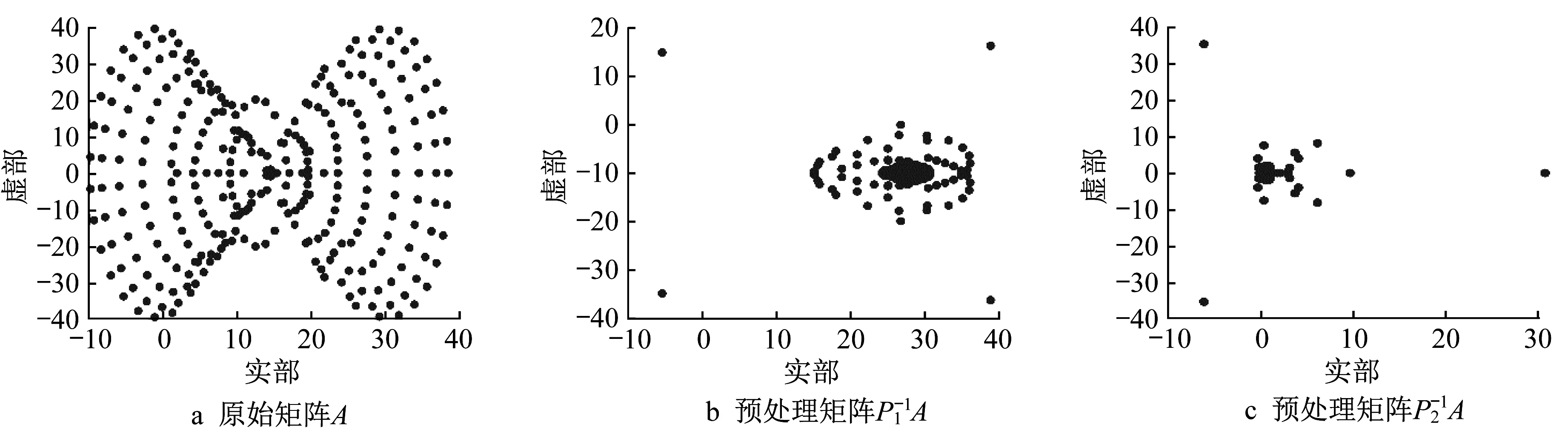
图1 算例1中N为300时,矩阵特征值分布图Fig.1 When N is 300 in Example 1,the eigenvalue distribution of the matrix
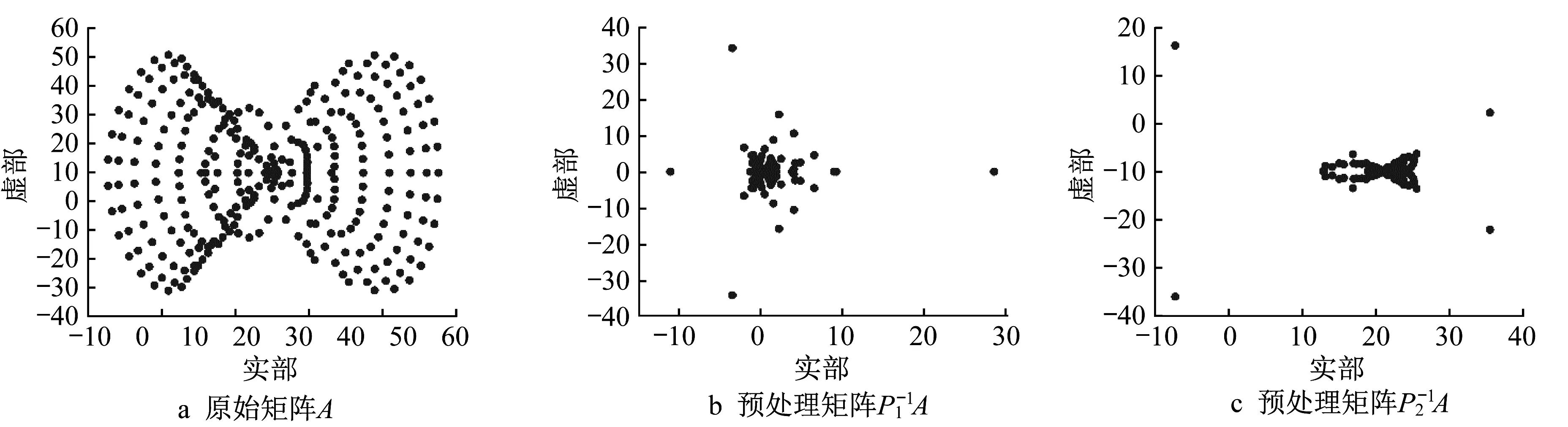
图2 算例2中N为300时,矩阵特征值分布图Fig.2 When N is 300 in Example 2,the eigenvalue distribution of the matrix
4 总结与展望
利用快速配置法数值离散变系数非局部扩散模型所得到的一类具有Toeplitz 结构的线性方程组的求解,针对系数矩阵的特殊结构,构造了一个Toeplitz 预处理子和循环预处理子,并将其应用于GMRES方法中,即得到预处理GMRES方法。最后利用数值实验验证了预处理GMRES方法的有效性。
非局部扩散模型的数值方法有待进一步研究,接下来可以考虑从数值离散方法入手,提出新的离散方法,保证线性系统更易求解。
