基于性能指标融合的随机退化系统竞争失效分析

董庆来, 王伟伟, 司书宾

(1.延安大学 数学与计算机科学学院, 陕西 延安 716000; 2.西北工业大学 机电学院, 陕西 西安 710072)

关于随机退化系统的研究可以追溯到20世纪60年代，但是直到20世纪90年代才引起国内外学者的重视，近年来随着传感器技术和计算技术的发展，随机退化系统的可靠性建模与分析已经发展为可靠性理论与工程领域研究的热点之一[1-4]。目前，在多元随机退化系统的研究中，通常假设系统的退化程度由每个性能指标的退化量直接进行描述[5];除此之外，在实践中，还经常将性能指标融合成一个变量间接地描述系统的健康状态[6]。例如，船舶艉轴承是船舶动力装置的主要组成部分，艉轴承间隙是描述船舶艉轴承健康状态的重要指标，而艉轴承间隙可通过艉轴直径磨损量和艉轴承衬磨损量来确定，当艉轴直径磨损量和艉轴承衬磨损量之和(即将二者融合为一个新的变量)达到失效阈值(即允许的间隙最大值)时，船舶艉轴承失效[7]。杨圆鉴[7]采用Wiener过程描述艉轴直径磨损量和艉轴承衬磨损量的退化过程，对船舶艉轴承的可靠性进行了评估，但是为了计算方便，假设二者是相互独立的。实际上，由于受共同的工作环境及应力影响，艉轴直径磨损量和艉轴承衬磨损量的退化过程是相关的，并且系统性能指标退化过程的相关性在许多系统中广泛存在，因此在多元随机退化系统的可靠性建模与分析中考虑性能指标的相关性更加符合实际，但是多元性能指标之间的相关性却给退化建模带来了巨大的挑战[4,8]，其主要原因在于多元随机过程(例如多元Wiener过程)的首达时分布是目前学术界无法解决的难题[9]。作为多元随机退化系统的特殊情形，二元随机退化系统是最基本、最重要的情形，是研究多元随机退化系统的基础，不仅能够反映多元情形下的许多本质问题，而且相比多元情形在数学上更易于处理[10]，因此本文以二元随机退化系统为主要研究对象。

在随机退化系统的可靠性建模中，除了建立描述系统退化过程的退化模型，还要确定系统失效的准则，两者缺一不可。学者们通常将系统的寿命定义为退化过程关于失效阈值的首达时间，一般称这种失效为退化失效[11-13]。事实上，许多系统的退化过程存在警戒阈值[14]，在退化量达到警戒阈值前，系统处于正常状态，但是超过警戒阈值后，系统将处于缺陷状态，例如警戒水位、腐蚀裕量等[15-16]，系统在2种状态下的退化速率通常是不同的。此时，如果采用相同参数的随机过程对系统两阶段退化过程进行描述，可能会导致可靠性指标计算的误差[17]。此外，上述系统除了发生因退化导致的退化失效外，系统还会发生突发失效[18-19]，例如系统在缺陷状态的持续时间过长，系统也会失效。Dong和Cui[20]考虑退化失效和持续时间失效，构建了基于非平稳随机过程的两阶段退化模型，给出了系统可靠度等可靠性指标。Qiu和Cui[21]考虑不同失效准则，给出了最优维修策略。上述文献均以一元随机退化系统为研究对象，而在二元或多元随机退化系统的可靠性建模与分析中均只考虑退化失效[22-26]，因此探讨二元或多元随机退化系统的竞争失效分析问题具有重要的现实意义。

基于上述分析，本文的主要研究内容包括：①针对二元随机退化系统，考虑性能指标的相关性、性能指标融合以及退化失效和持续时间失效2类竞争失效形式，构建基于二元Wiener过程的可靠性模型。②在性能指标不进行融合以及性能指标按照退化量的线性组合进行融合情形下，推导持续时间失效阈值为常数和随机变量时的系统可靠度解析表达式。③提出基于蒙特卡洛模拟的数值模拟算法,模拟性能指标按照任意形式进行融合情形下二元以及多元随机退化系统的可靠度，并用于验证解析结果的正确性。

1 问题描述与可靠性建模

考虑二元随机退化系统，根据性能指标是否进行融合，构建2个可靠性模型。性能指标融合是指利用新变量描述性能指标之间的关系，即系统的退化程度由性能指标退化量的函数进行描述。假设X(t)=(X1(t),X2(t))′,Xi(t)为系统的第i个性能指标在时刻t的退化量(i=1,2),则在性能指标融合情形下,系统在时刻t的退化程度由X(t)的函数H(x1,x2)进行描述,其中x1和x2为X1(t)和X2(t)的样本实现值。

模型1性能指标不进行融合情形下的可靠性模型。

1) 两阶段退化过程

假设系统的退化过程包括正常阶段(或第一阶段,即从新系统投入运行到缺陷发生时刻)和缺陷阶段(或第二阶段,即从缺陷发生时刻到失效发生时刻),从而系统的状态包括正常、缺陷和失效。令

(1)

式中:Xik(t)是系统的第i个性能指标在第k个阶段时刻t的退化量,i=1,2,k=1,2;Γ1是变点,定义为2个性能指标首达警戒阈值的时刻,若定义随机变量γi=inf{t>0:Xi1(t)≥Di1},i=1,2,则Γ1=min{γ1,γ2}。

2) 二元Wiener过程退化模型

由于受共同的环境应力,2个性能指标的退化过程是相关的,在每个阶段采用二元相关Wiener过程描述系统的退化程度,即

X(t)=

(2)

式中:x0=(x110,x210)′是系统的初始退化量,并假设x0=(0,0)′,即系统在时刻t=0是全新的;X(Γ1)=(X11(Γ1),X21(Γ1))′为系统在变点处的退化量向量。对于i=1,2,k=1,2,μk=(μ1k,μ2k)′为漂移系数向量;μik为系统第i个性能指标在第k个阶段的漂移系数;Σk是第k个阶段的扩散矩阵,使得

为协方差矩阵,ρk是相关系数,描述2个性能指标在第k个阶段的相关性,σ1k和σ2k为标准差;W(t)=(W1(t),W2(t))′,{W1(t),t≥0}和{W2(t),t≥0}是相互独立的标准Wiener过程。具体的,如果记

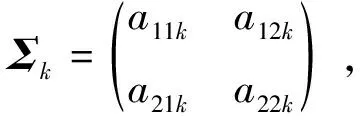
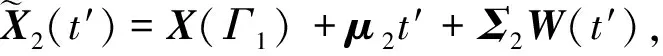
3) 竞争失效

当一个性能指标的退化量超过其退化失效阈值时,或系统在缺陷阶段的持续时间超过持续时间失效阈值τ时,系统失效。系统的退化路径如图1所示,其中γ和y分别为Γ1和Y的实现值。

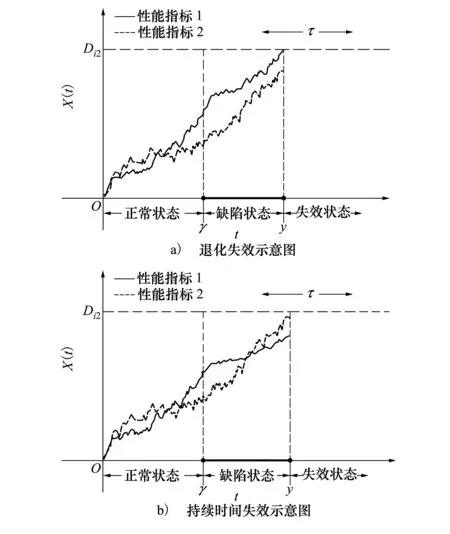
图1 模型1下系统的退化路径

因此,模型1下系统的寿命为

Y1=min{Λ1,τ}+Γ1

(3)

模型2性能指标融合情形下的可靠性模型。

本文考虑H(x1,x2)的3种表达形式:

①H(x1,x2)=k1x1(t)+k2x2(t),k1,k2∈R;②H(x1,x2)=|x1(t)-x2(t)|;③一般形式。

与模型1的不同之处在于变点以及系统寿命的表达形式。在模型2下,变点定义为2个性能指标退化量的函数关于警戒阈值L1的首达时刻,即

Γ2=inf{t≥0:H(X11(t),X21(t))≥L1}

(4)

则系统的寿命为

Y2=min{Λ2,τ}+Γ2,

(5)

2 系统可靠度

本节将给出系统可靠度的解析表达式,包括模型1和模型2下H(x1,x2)=k时2种情形,以及模型2下H(x1,x2)为一般函数时可靠度的模拟算法。

1) 模型1下系统可靠度

根据失效准则,系统的可靠度为

R(t)=P{Y1>t}=P{min{Λ1,τ}+Γ1>t}

(6)

首先,假设持续时间失效阈值为常数。

注意到Γ1=min{γ1,γ2}以及γi=inf{t≥0:Xi(t)≥Di1},i=1,2,通过对一个性能指标达到失效阈值的时刻及另一个未达到失效阈值的性能指标在该时刻的数值取条件,得到

(7)

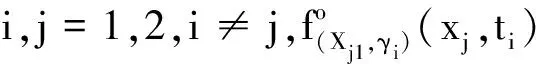
当其中的一个性能指标达到失效阈值时,系统将进入缺陷阶段。根据Xi2(t)(i=1,2)的定义,当

(8)

式中,f(λ1,λ2)(u1,u2|x0i)的表达式由文献[27]的公式(2)给出。将(8)式代入(7)式,得到

(9)

在工程实践中,持续时间失效阈值通常是随机变量。下面假设持续时间失效阈值是具有概率密度函数fτ(t)和分布函数Fτ(t)的随机变量,并考虑以下2种情形：一种情形是分布在[0,+∞)上的随机变量;一种情形是分布在[τ1,τ2]上的随机变量,其中τ1和τ2是正常数。

如果持续时间失效阈值τ是分布在[0,+∞)上的随机变量,例如τ是服从指数分布或韦布尔分布的随机变量,则(9)式变为

类似的,可以得到持续时间失效阈值τ是分布在[τ1,τ2]上的随机变量时的可靠度。

2) 模型2下H(x1,x2)=k时系统可靠度

根据Γ2的定义,如果τ是常数,系统可靠度为

(10)

式中:f(X1,Γ2)(x1,u)是X1(Γ2)和Γ2的联合概率密度函数,满足

f(X1,Γ2)(x1,u)=fX11(u)(x1)fΓ2(u)

(11)

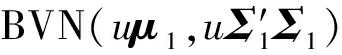
(12)

从而,要得到(11)式的解析表达式,只需得到变点Γ2的概率密度函数fΓ2(u)即可。然而,除了H(x1,x2)的一些特殊形式外,fΓ2(u)的解析表达式是很难获得的。

下面,给出H(x1,x2)=k1x1+k2x2情形下的系统可靠度。由(2)式知

H(X11(t),X21(t))=(k1μ11+k2μ21)t+δ1B1(t)

(13)

式中，{B1(t)=[(k1a111+k2a211)W1(t)+(k1a121+k2a221)W2(t)]/δ1,t≥0}是标准Wiener过程，

由Γ2的定义,即Γ2=inf{t>0:H(X11(t),X21(t))≥L1},fΓ2(u)为{Z1(t),t≥0}关于L1的首达时的概率密度函数,其中Z1(t)(k1μ11+k2μ21)t+δ1B1(t)。因此,由(13)式可以得到

(14)

将(12)式和(14)式代入(11)式,得到

(15)

接下来,给出FΛ2(t-u|x1,x2)的解析表达式。注意到k1x1+k2x2=L1,与(13)式类似

L1+(k1μ12+k2μ22)t+δ2B2(t),t≥0

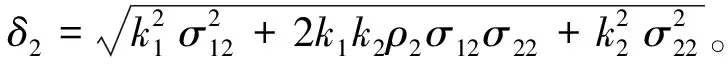
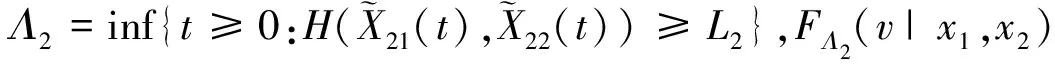
(16)

将(15)式和(16)式代入(10)式,得到H(x1,x2)=k1x1+k2x2情形下的系统可靠度

(17)

注：①如果令τ=0,(17)式将变为单阶段一元随机退化系统的可靠度[11];②如果令τ→+∞,(17)式将变为两阶段一元随机退化系统的可靠度[11];③如果τ是随机变量,通过积分可以得到相应的系统可靠度的解析表达式。

3) 模型2下H(x1,x2)为一般函数时系统可靠度的数值模拟

由(11)式可以发现,性能指标按照任意形式进行融合情形下的系统可靠度表达式在形式上是简单的,但是对一般H(x1,x2)而言,Λ2和Γ2的分布函数的表达式并不容易求解。基于蒙特卡洛模拟的算法来模拟系统可靠度,具体的模拟算法流程如算法1所示。

算法1模型2下H(x1,x2)为一般函数时系统可靠度的模拟算法

步骤1设定参数值,包括初始时刻t=0,初始退化量x0,漂移参数向量μ1和μ2,扩散矩阵Σ1和Σ2,警戒阈值L1,退化失效阈值L2,持续时间失效阈值τ和其他相关参数。令模拟次数和步长分别为N和Δt。

步骤2对于i=1,2,…,N,执行步骤3至4。

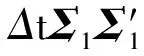
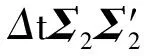
步骤5完成模拟,根据失效数据集A计算系统可靠度。

注：1) 如果持续时间失效阈值是随机变量,只需在步骤4中增加在指定的分布中生成独立同分布的随机数即可。

2) 算法1还适用于基于性能指标融合的多元随机退化系统的可靠度计算,即随机退化系统具有多个性能指标(例如n个性能指标)时,只需做如下修改:①在步骤3和步骤4中生成多元正态分布随机数,即扩散矩阵Σ1和Σ2分别为n×n阶矩阵;②采用H(x1,x2,…,xn)描述性能指标融合,即将各性能指标退化量的数值代入H(x1,x2,…,xn)描述系统的退化程度。

3 数值算例

本节给出一些数值算例来验证所构建模型的有效性,并对模型中的参数进行灵敏度分析,探讨模型参数对随机退化系统可靠性指标的影响。

假设2个性能指标退化量的警戒阈值和退化失效阈值分别为0.2和0.4,持续时间失效阈值τ=4。在第一阶段,μ11=μ21=0.016 7,σ11=σ21=0.045 0,ρ1=-0.786 2;在第二阶段,μ12=μ22=0.024 0,σ12=σ22=0.060 4,ρ2=-0.694 3,从而两阶段的协方差矩阵分别为

1) 模型1下系统可靠度

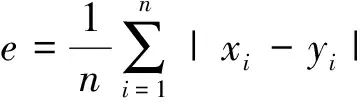
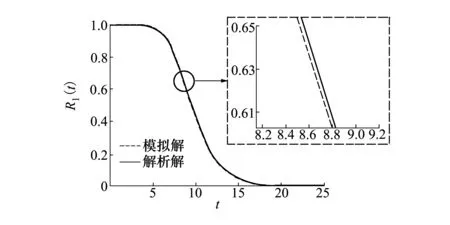
图2 模型1下基于模拟解和解析解的系统度曲线

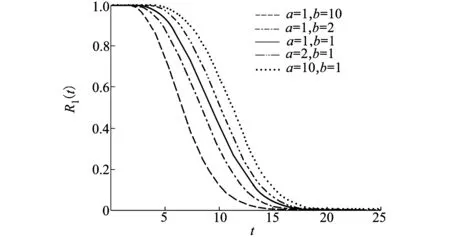
图3 持续时间失效阈值服从β分布情形下系统可靠度曲线

2) 模型2下H(x1,x2)=k1x1+k2x2时系统可靠度

假设系统的警戒阈值、退化失效阈值和持续时间失效阈值分别为0.3，0.5和4.0,其余参数取值与图3相同。为了描述2个性能指标退化量的线性组合对系统可靠度的影响,考虑k1和k2取不同参数值情形下的系统可靠度,即:k1=1.5且k2=1.2、k1=1且k2=1、k1=0.5且k2=0.5、k1=0.4且k2=0.3、k1=1且k2=0。将可靠度曲线画在同一个图中,如图4所示,其中k1=1且k2=0时的系统可靠度曲线可以看作一元随机退化系统的可靠度曲线。

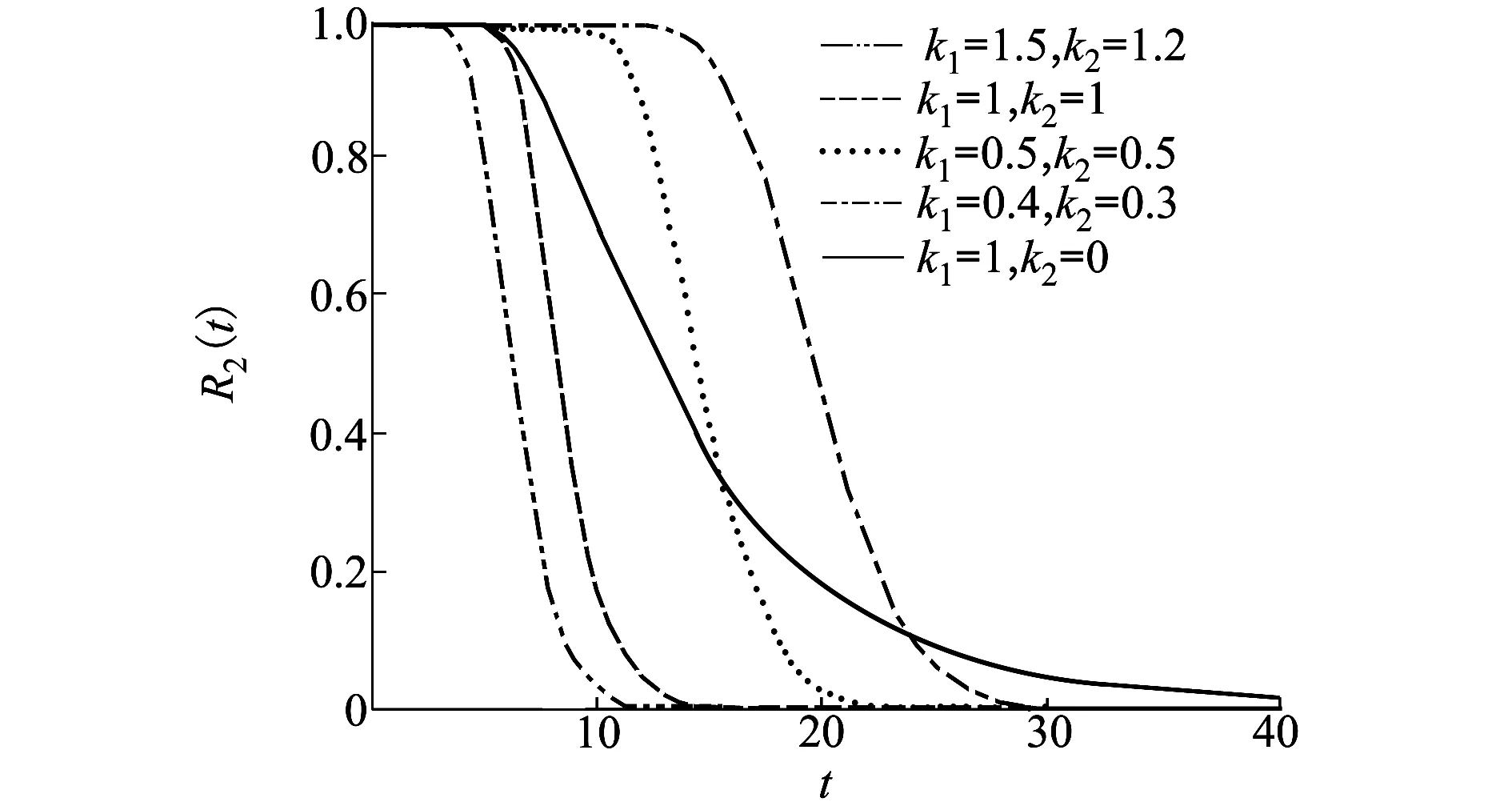
图4 H(x1,x2)=k1x1+k2x2情形下系统可靠度曲线

从图4可以发现,k1和k2的值越大,系统的可靠度越低。这是因为k1和k2反映了2个性能指标退化量对系统整体退化量的贡献,它们的值越大,说明系统的退化速度越快,从而系统的可靠度越低,这与我们的直觉是一致的。另一个现象是,当k1和k2的取值较小时,其可靠度在退化过程的早期阶段高于单变量Wiener过程退化模型的结果,而在退化过程的后期结果却相反,这可以用2个性能指标的相关性(2个性能指标是负相关的)来解释。

3) 模型2下H(x1,x2)=|x1-x2|时系统可靠度分析

不等式|x1-x2|>L1曾被Cui等[8]用作平衡系统的失效准则,即当2个性能指标退化量的距离大于失效阈值L1时,系统失效;采用Markov过程描述2个性能指标的退化过程,并假设它们是相互独立的。下面,利用算法1给出2个性能指标相关时采用函数H(x1,x2)=|x1-x2|描述系统退化程度情形下的系统可靠度曲线。假设τ=0,L1=0.1,即只考虑单阶段退化过程。为了得到2个性能指标之间的相关性对系统可靠度的影响,分别令ρ1=-0.8，-0.5，0，0.5和0.8,将可靠度曲线画在同一个图中,如图5所示。其余参数取值与图2相同。从图5可以发现,在其余参数值相同的情形下,相关系数ρ1的值越大,系统的可靠度越高。因此,2个性能指标的退化过程是正相关(或负相关)时,如果假设它们彼此独立,则会低估(或高估)系统可靠度。

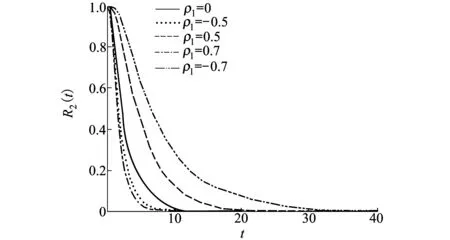
图5 模型2下H(x1,x2)=|x1-x2|时单阶段随机退化系统可靠度曲线

图6 模型2下H(x1,x2)=|x1-x2|时两阶段随机退化系统可靠度曲线

进一步,为了探究持续时间失效阈值对系统可靠度的影响,假设L1=0.1,L2=0.3,其余参数取值与图3相同,考虑τ取不同参数值情形下的系统可靠度,包括τ=0,4,7,10和50,并将可靠度曲线画在同一个图中,如图6所示。从图6可以发现,持续时间失效阈值越小,系统的可靠度越低。这意味着系统处于缺陷阶段的可承受时间越短,系统发生失效的可能性越大,这与文献[20]的结论是一致的。

4 结 论

本文针对二元随机退化系统，考虑性能指标融合以及竞争失效，提出了基于二元相关Wiener过程的退化模型，给出了性能指标不进行融合以及性能指标按照退化量的线性组合进行融合情形下，持续时间失效阈值为常数和随机变量时的系统可靠度的解析表达式。当性能指标按照任意形式进行融合时，提出了一个算法程序来模拟系统的可靠度。研究结果表明持续时间失效阈值越大，系统的可靠性越高。此外，当性能指标按照2个性能指标退化量的距离进行融合时，若2个性能指标正相关(或负相关)而假设它们彼此独立，则会低估(或高估)系统可靠度。因此，在工程实践中，如果存在2个(或多个)性能指标，应充分考虑它们的相关性，从而提高可靠性指标计算的精度。此外，本文给出的算法尽管能够用于性能指标按照任意形式进行融合情形下二元以及多元随机退化系统可靠度的模拟，但是由于该算法是基于蒙特卡洛模拟的，因此算法的精度强烈依赖于模拟次数，因此在今后研究中寻求系统可靠度的解析表达式以及其他算法将更加有意义。