基于威胁建模的UCAV武器投放在线航迹规划

唐嘉钰, 李相民, 代进进

(1. 海军航空大学, 山东 烟台 264001; 2.海军研究院, 北京 100422)

攻击型无人机(unmanned combat aerial vehicle,UCAV)是快速形成对敌威胁、打赢信息化条件下非对称战争的重要手段[1]。UCAV可携带小型或大威力的精确制导武器(包括反辐射导弹、红外制导导弹及制导炸弹等) ，可遂行防空压制、对地攻击等作战任务[2]。

航迹规划技术是成功实现UCAV自主攻击的关键技术之一[3]。目前无人机航迹规划方法主要有Voronoi图算法[4-6]、A*算法[7-8]、稀疏A*(sparse A*search,SAS)算法[9]、人工势场法[10-12]、灰狼算法[13-14]和随机搜索树(rapid-exploration random tree,RRT)算法[15-16]，在线航迹规划则主要通过滚动时域控制获取实时动态飞行轨迹[17-20]。目前UCAV航迹规划研究主要集中于局部威胁信息已知的静态任务场景，未考虑复杂战场环境动态变化(例如突发威胁和机动目标等)。

针对这一问题，本文提出了基于任务区域威胁建模的UCAV在线投放航迹规划方法。首先，针对UCAV对地攻击任务需求，将预先求解的机载制导炸弹可投放区中心和投放姿态作为终端约束条件，同时考虑飞行器性能和战场环境等约束，建立了UCAV武器投放航迹规划模型；基于战场环境威胁建模，结合模型预测控制的滚动优化策略，UCAV通过不断在线预测判断飞行态势实现自主避障飞行。仿真结果表明，本文所提算法能够实现UCAV在动态战场环境下在线航迹规划。

1 UCAV武器投放航迹规划数学模型

1.1 UCAV运动学及动力学模型

与旋翼飞机相比，固定翼无人作战飞机具有续航能力强、飞行速度快及可靠性较高等优点，更适合应对复杂动态多变的战场环境。

UCAV在地理坐标系下的质点运动学和动力学方程组分别为

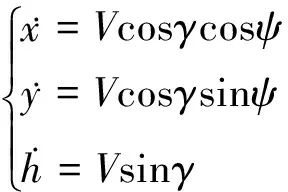
(1)

(2)

(3)

式中:δ为UCAV油门位置;Tmax为UCAV最大可用推力;ρ为空气密度;S为飞行器横截面积;CD和CL分别为阻力和升力系数。

1.2 UCAV机载武器可投放区模型

为保证机载武器命中精度、提升攻击效果,UCAV投放制导炸弹时存在特定的区域限制,这个区域即为可投放区。当UCAV在此空域内且满足投放速度姿态等约束条件时投放制导炸弹,制导炸弹将以给定精度命中目标,而在此区域外进行投放时,则无法保证有效地命中目标。因此,UCAV在航迹规划前应依据目标类型和毁伤特性等要素,解算出制导炸弹的可投放区,以此作为航迹规划的末端约束条件,确保UCAV完成攻击前的占位。

1.2.1 制导炸弹运动学模型

1) 制导炸弹弹道模型

计算制导炸弹可投放区的本质是生成炸弹弹道航迹,为提高计算效率,本文采用三自由度质点运动模型,同时为了便于模型的建立与求解,做以下假设:

(1) 不考虑外界环境因素对炸弹弹道航迹的干扰,飞行条件设定为标准大气环境;

(2) 忽略炸弹弹体的转动惯性,不研究炸弹在飞行过程中绕质点转动的情况;

(3) 弹上测量和控制系统能够准确、理想无延迟工作。

制导炸弹弹体运动学方程与(1)式相同,其动力学方程则为

(4)

2) 制导律模型

UCAV机载制导炸弹采用比例导引律,不考虑滚转角及滚转角速率影响,可将制导炸弹在三维空间上的运动解耦成俯冲和转弯2个平面上的运动。

制导炸弹视线角速率为

(5)

式中:(lm,pm,sm)表示投放后制导炸弹位置,其中lm代表纵向射程;pm代表侧向射程;(lT,pT,sT)代表目标点位置;qd和qt分别为视线在俯冲平面内的高低角和转弯平面内的方位角,则为制导炸弹与目标相对距离

(6)

考虑制导炸弹采用传统比例导引律,则有

(7)

式中,Kd和Kt为比例导引律的增益。

1.2.2 制导炸弹可投放区模型

可投放区模型的求解主要包括两方面内容:通过计算极限射程弹道获得制导炸弹可达域;将可达域变换得到可投放区边界。可投放区求解流程如图1所示。

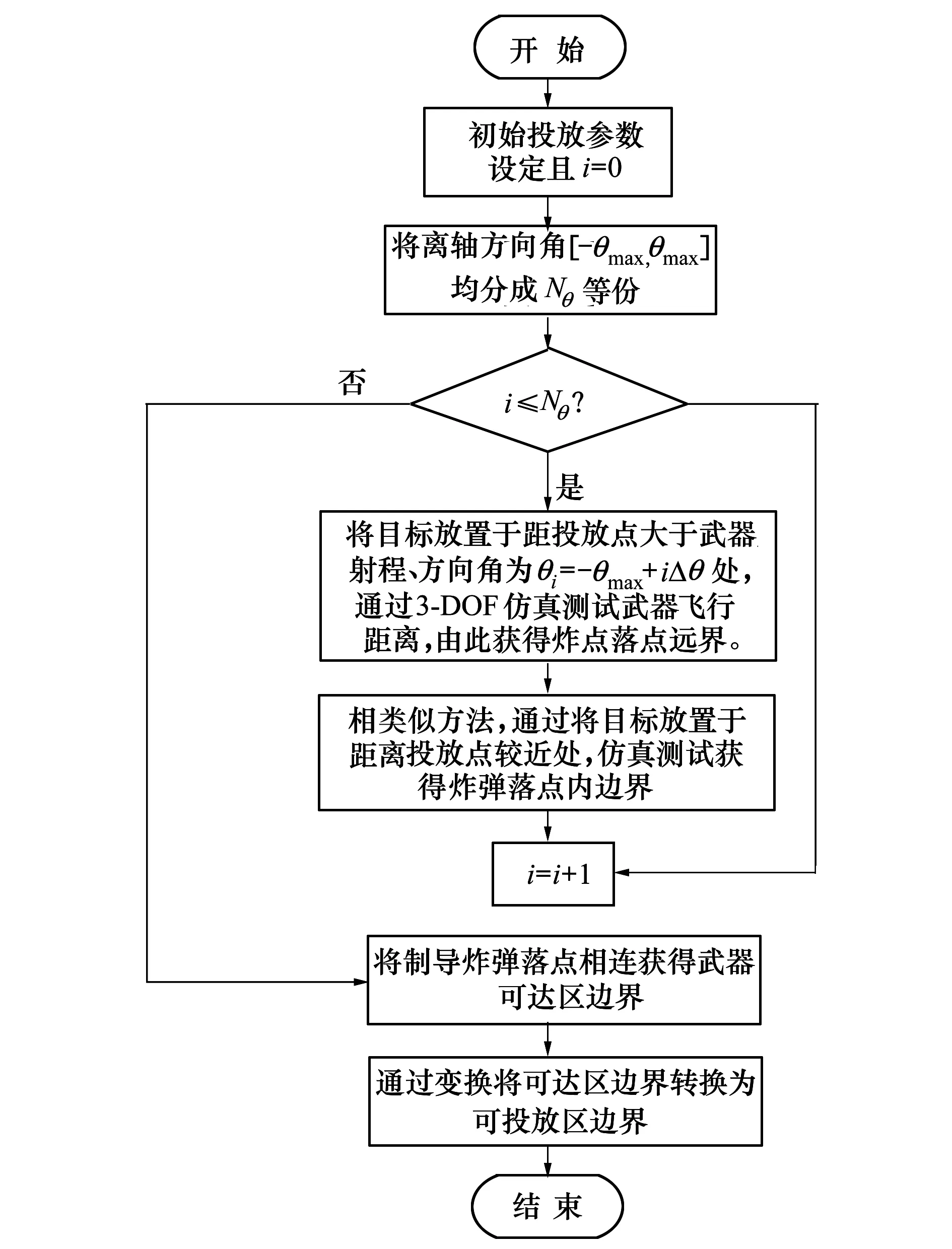
图1 机载制导炸弹可投放区包络求解流程

1.3 UCAV武器投放航迹规划约束条件

UCAV武器投放航迹规划时需满足边值和过程约束两类约束条件。

1.3.1 边值约束条件

边值约束条件主要包括初值约束和终端约束。

1) 初值约束

设任务起始时刻为ts,则初值约束为

(8)

2) 终端约束

(9)

式中:(xj,yj)为第j个可投放区包络顶点;Np为包络顶点个数。因此UCAV投放航迹终端约束为

(10)

式中:ε为地理坐标系下所允许的距离偏差;xf,yf及hf分别为UCAV航迹末端点位置。

此外,在武器投放点UCAV还需要满足一定的速度和姿态约束,即

(11)

式中:tf为终端时刻；Vrelease为武器投放速度；γrelease为投放航迹倾角；αrelease为投放迎角；ψrelease为投放滚转角。

1.3.2 过程约束条件

飞行过程中,UCAV需满足机动性能约束和战场环境约束。

1) 机动性能约束

机动性能约束条件主要包括航迹控制量、速度、加速度、航向角及最小转弯半径等约束。根据UCAV机动性能,具体建立如下过程约束条件

(12)

2) 战场环境约束

UCAV在对地攻击过程中会碰到地形障碍及防空阵地等安全威胁。飞行过程中UCAV应尽可能避开这些威胁,同时与目标保持一定距离以保证自身安全。

战场环境约束条件主要分为硬威胁和软威胁2类。硬威胁是指无人机无法进入的障碍区域,例如山体、建筑物及其他禁飞区;软威胁则是指与防空武器相关的安全威胁,例如地空导弹、防空火炮等。

(1) 硬威胁模型

以圆柱体作为硬威胁基本形状,设共有M1个互不联通的硬威胁Hm=〈Am,Pm〉,m=1,…,M1,其中Am为圆柱体中心点坐标;Pm为形状参数矩阵,特别的,Pm=diag(a2,b2,c2)时圆柱体三轴分别与x轴、y轴和z轴平行,当a=b=c=r时Pm表示半径为r的球体,Pm中非对角线元素不为零则表示威胁体坐标轴与航迹坐标系轴之间存在非零夹角。考虑到硬威胁三维模型中Am和Pm难以确定,在UCAV定高飞行模式下,将Am和Pm简化为二维形式更易于计算。因此在高度为h处,硬威胁Hm可由二维中心点坐标Am(h)和形状参数矩阵Pm(h)共同确定。

综上UCAV硬威胁度函数可定义为

Fm(p(h))=

(13)

式中,p(h)=(x,y)表示在飞行高度为h时UCAV在2D平面内位置坐标。当Fm(p(h))<0时,UCAV可成功躲避硬威胁Hm。

(2) 软威胁模型

与硬威胁不同,UCAV与软威胁之间不存在碰撞问题,无人机应尽可能远离软威胁。设共有M2个软威胁,飞行高度为h时,第j(j=1,…,M2)个软威胁对UCAV的威胁度函数可表示为

Ωj(p(h))=

(14)

式中:λ(h)为与高度h有关的软威胁强度系数;Bj(h)和Qj(h)≥0分别为第j个软威胁位置和威胁区域半径。当UCAV以恒定高度飞行或飞行高度变化不大时,λ(h)可设为1。

软威胁度函数Ωj(p(h))表征了UCAV位于(x,y,h)时被第j个软威胁击中或摧毁的概率。通过将所有软威胁的威胁度叠加,可获得整体软威胁度,即

(15)

Ω(p(h))数值越小,表明UCAV受到的软威胁程度越低。

1.4 UCAV航迹规划目标函数

UCAV投放航迹规划目标主要可分为3个方面:①尽可能接近机载武器投放区中心点;②避免与硬威胁发生碰撞;③尽可能远离软威胁。据此UCAV最优路径转化为以下最优控制问题

(16)

由于战场环境具有动态多变、复杂不确定的特点,UCAV对战场态势信息很难具备准确的先验知识,一般只能依靠其传感器来对局部环境信息进行探测。因此,引入了模型预测控制(model predictive control,MPC)中的滚动规划策略将航迹规划控制在一个移动区域中滚动进行,根据其时空约束条件控制每次滚动的优化范围,保证无人机航迹规划的实时性。

因此,上述航迹规划最优控制问题模型可进一步转化为

(17)

式中:δ为时域长度;Δt为单位时间步长。为保证求解精度,δ和Δt取值不宜过大,但二者数值较小将导致计算负担增大。本文中设δ=1。

2 基于威胁建模的UCAV在线航迹规划算法

2.1 在线航迹规划关键要素

设UAVi当前状态量SUAVi(k)由二元组〈pUAVi(k),VUAVi(k)〉表示,其中pUAVi(k)=(xUAVi(k),yUAVi(k),hUAVi(k))T为无人机位置坐标,VUAVi(k)为无人机速度。为便于分析,仅考虑UCAV以定高模式飞行,即hUAVi(k)≡hUAVi。由UCAV质点运动学方程可知,单位时间步长后UCAV速度和航向角变化范围为

(18)

[max{VUAVi+amin·Δt,Vmin},

min{VUAVi+amax·Δt,Vmax}]

(19)

UAVi与投放区中心qTi之间的视线角为

(20)

此时UAVi以最大和最小转弯率能到的极限距离分别为

2.2 威胁规避策略

下面分别计算UCAV飞行过程中遭遇硬威胁和软威胁时航向角的最优变化范围。

1) 硬威胁避碰策略

为了保证UCAV飞行安全,其航向角变化范围为

(23)

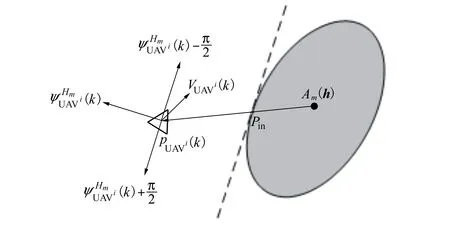
图2 UCAV躲避硬威胁航向角变化

由图2可得,与Pin处切线垂直的2个方向为

(24)

式中

(1) 当yUAVi(k)=ay时,有

yin=ay

(2) 当yUAVi(k)≠ay时,有

式中

2) 软威胁躲避策略

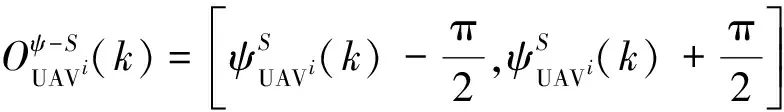
(25)

式中

2.3 基于威胁建模的在线航迹规划流程

依据建立的硬、软威胁模型,UCAV飞行态势可分为以下4种情况:

Case 1 若UCAV保持当前速度飞行,大概率会与硬威胁Hm发生碰撞,UAVi需最大程度降低速度,以尽快转弯实现避障;

Case 2 若UCAV继续保持当前速度飞行,飞行器很可能进入高危区域,此时UAVi同样需尽快降低速度,远离高危区域;

Case 3 UCAV可安全飞行但距离投放区较远,此时UAVi应保持当前航向,尽快飞往可投放区。

Case 4 UCAV距离投放区中心的距离已经满足任务要求,此时UAVi应调整姿态,准备完成机载武器投放。

根据上述UCAV飞行态势分析,在线航迹规划过程中,定义如下2个态势判别变量

(26)

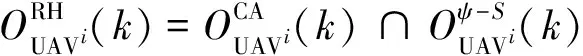
(27)

表1态势状态变量与UCAV飞行态势对应关系

图3 基于威胁建模的武器投放在线航迹规划流程

3 仿真结果及分析

以攻击型无人机执行对地攻击任务为例,对文中提出的武器投放航迹在线规划算法进行仿真验证。

设定多无人机之间为全连通通信网络。仿真实验环境硬件为Intel(R)Core(TM)i7-2630QM CPU 2.00 GHz,Win 7操作系统,应用基于MATLAB R2019a的GPOPS工具包获得控制参数。

3.1 任务环境想定

UCAV性能参数如表2所示。任务仿真想定如下:UCAV初始位置为(2,3,1.5)km,地面静态目标位置为(14,14,0)km,初始速度为V0=200 m/s,初始航向角ψ0=135°,γ0=0,初始载油量为mfull=3 000 kg。

硬威胁为建筑物,软威胁分别是雷达和防空导弹阵地。机载制导武器投放速度Vrelease=250 m/s,γrelease=0°,ψrelease∈[-10°,10°],αrelease=0°。C1=C2=0.5,软威胁度阈值ξ=0.6,εRH=1 km。起始时刻为t0=0,Δt=1 s。

表2 UCAV性能参数

3.2 场景1:静态场景航迹规划仿真分析

场景1中UCAV起始位置为(2, 3,1.5)km,地面固定目标位于(14,14,0)km处。战场环境如3.1节所示。规划航迹结果如图4所示(图中红色线条代表UCAV飞行航迹,蓝色线条表示制导炸弹弹道)。算法运行时间为8.42 s,总飞行时长为90 s。

图4 UCAV武器投放航迹

由图4可以看出,本文所提出的在线规划策略生成航迹较为光滑,UCAV能够灵活避开软、硬威胁,成功达到可投放区中心点附近。武器投放点距离可投放区中心点0.258 0 km。

3.3 场景2:动态场景航迹规划仿真分析

为了验证UCAV武器投放在线航迹规划方法的可行性与有效性,场景2中对突发机动威胁和机动目标的情况进行仿真实验。机动威胁为敌方UCAV,威胁半径为0.5 km,其预测速度为200 m/s,预测航向角为135°。地面机动目标以30 m/s的速度朝西北方向移动。

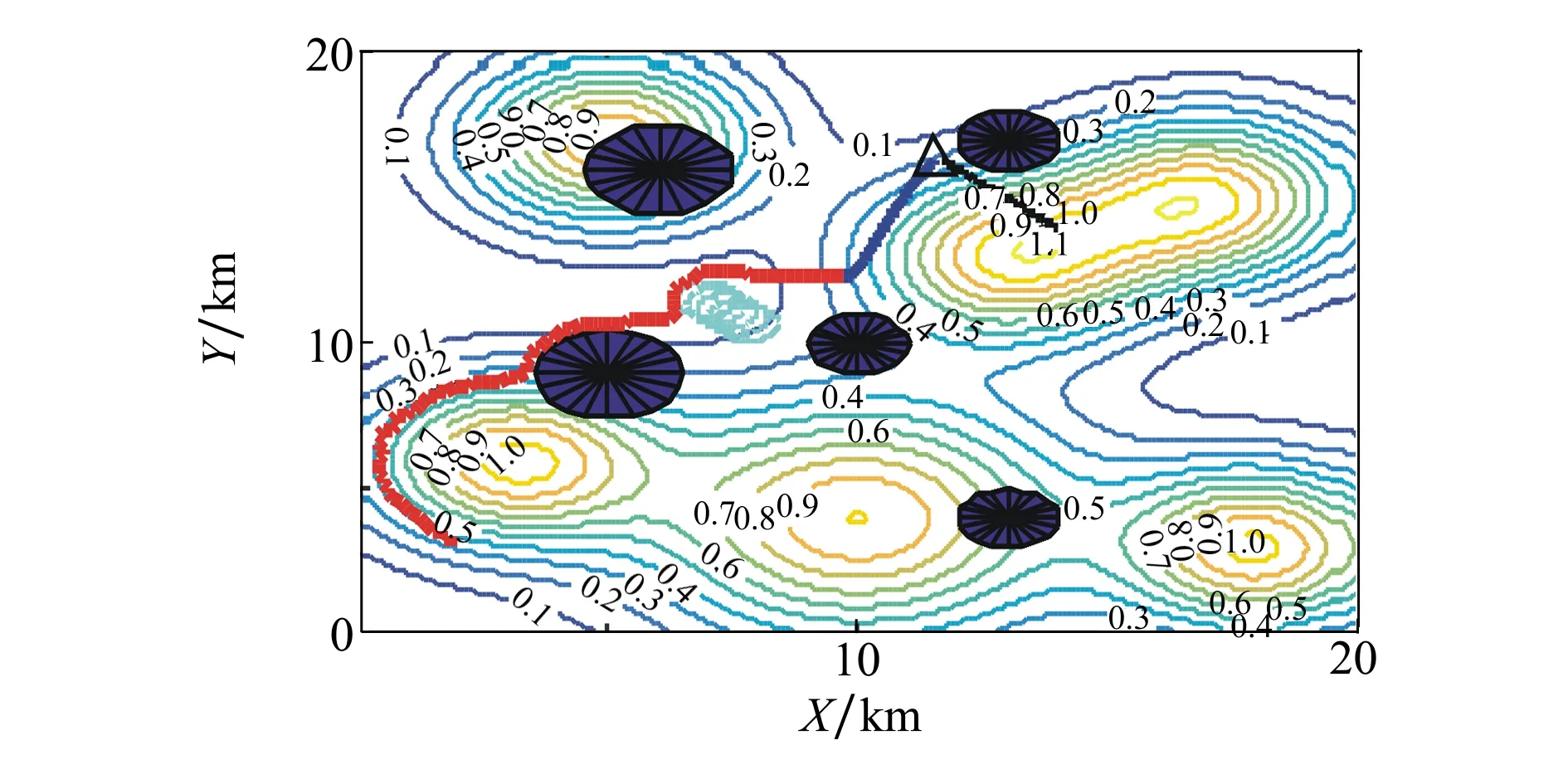
图5 突发机动威胁和机动目标下UCAV航迹

为了直观展示动态场景下UCAV在线规划航迹,图5给出了UCAV航迹的三维投影图。图中红色线条代表UCAV航迹,浅蓝色圆形代表突发机动威胁,深蓝色线段为制导炸弹航迹,黑色线段为机动目标轨迹。算法运行时间为9.35 s,总飞行时长为94 s。武器投放点距离可投放区中心点0.032 7 km。

由图5可知,本文所提算法可实现动态威胁场景下UCAV在线航迹规划。当飞行时间为71 s时,UCAV探测到突发机动威胁,通过改变控制参量实现降速并调整航向,成功避开突发威胁,并最终飞抵可投放区中心附近。当t=71 s时,UCAV侦察到突发机动威胁,依据威胁规避策略UCAV。本节仿真结果展示了本文所提在线轨迹规划算法对存在突发机动威胁和机动目标的动态场景的适用性。

3.4 算法性能比较

为进一步验证算法性能,将本文所提航迹规划算法与稀疏A*算法进行对比,2种算法静态航迹对比如图6所示,仿真参数设定同场景1。

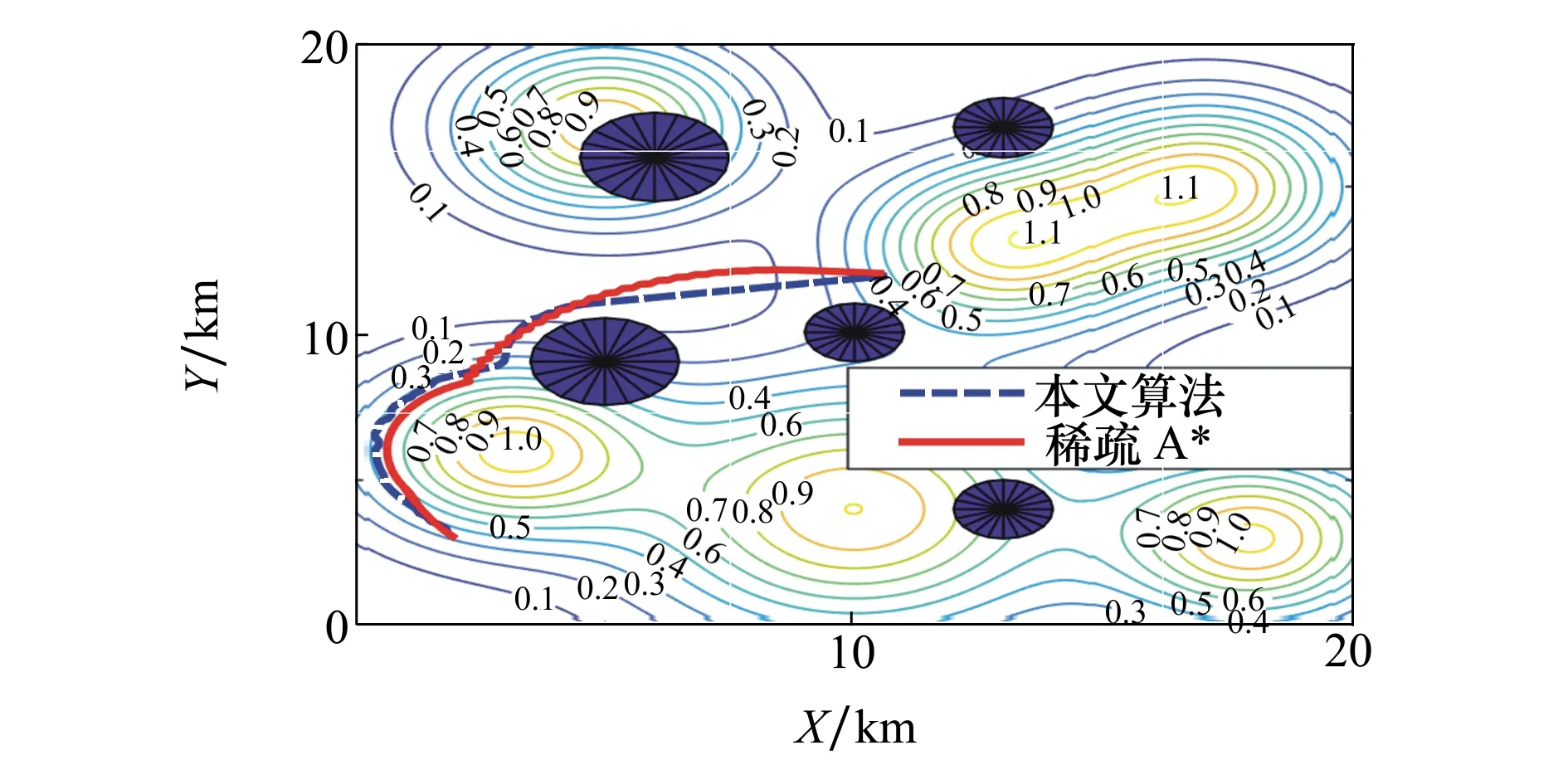
图6 算法静态场景航迹对比图

表3给出了2种算法在静态场景下的平均威胁代价(所有航迹点威胁代价的平均值)和航迹长度。

表3 算法静态场景性能比较

表4中,算法1为本文所提在线航迹规划算法,算法2为稀疏A*搜索算法。

由表4可以看出,基于本文所提算法在静态场景下规划的航迹长度最短且总威胁代价最小。

在实现静态航迹规划基础上随机产生动态威胁,移动威胁参数设定同场景2,动态场景下航迹规划仿真结果如图7所示。

图7 算法动态场景航迹对比图

表4给出了2种算法在动态场景下的平均威胁代价和航迹长度。

表4 算法动态场景性能比较

由表5可以看出,2种算法规划的航迹都较好躲避了突发动态威胁,基于本文所提算法在动态场景下规划的航迹平均威胁代价最小但飞行航迹长度稍长于SAS算法。

4 结 论

基于战场环境威胁建模,本文提出了一种考虑机载武器投放约束的固定翼UCAV确定性在线轨迹规划方法。仿真结果表明,本文设计的在线航迹规划策略可使得UCAV在成功进入制导炸弹可投放区的同时有效避开战场威胁。基于本文算法所得飞行轨迹质量随着时间步长取值缩小而增加,但与此同时算法计算量急剧增大。因此,如何将在线轨迹规划与基于智能优化算法的预先航路规划进行有效结合,并依据战场环境特性实现在线规划步长的自适应调整是后续研究的重点。