基于多航天器协同观测的空间非合作目标姿态参数在轨识别方法研究

赵迪, 孙冲, 袁建平, 袁静

(西北工业大学 航天学院, 陕西 西安 710072)

伴随着空间探索的不断深入和空间任务的不断升级[1]，空间非合作目标的信息测量和参数估计成为在轨服务任务的关键技术。尤其是近年来，随着空间航天器数量指数级增长，空间抓捕、碎片清理、轨道加注等在轨操作任务需求更为迫切[2-4]。而对缺乏先验信息的空间翻滚非合作目标的运动参数识别是上述非合作目标空间操作及在轨服务的前提和必要条件。由于缺少相关的几何构型等先验知识，也没有可用于合作的人工标记，导致传统的协同算法可能不再适用，给相对状态估计带来了很大的挑战。由于视觉感知的被动特性，基于视觉的方法在非合作目标相对状态估计研究中日益受到人们的关注和重视。

目前，针对已知目标模型或部分信息的“合作目标”的视觉测量己有了广泛的研究[5-8]，但应用于真正非合作目标的算法却很少。Biondi等[9]提出一种假定目标上存在合作的标识点或其3D几何构型已知的视觉观测方法。然而该方法需要特征点在目标坐标系中的坐标已知，只存在部分噪声，即假定已知目标的模型先验信息。Li等[10]提出了一种基于连续点云的空间目标状态估计方法，在不知道空间目标结构的情况下，实现了交会过程中对空间翻滚目标的状态估计。但该方法假定目标点云姿态测量数据已通过立体视觉观测粗略测得，即假定可以持续性地对目标进行有效观测，没有考虑到观测量不足的情况。

对于空间非合作目标，考虑到空间环境干扰造成的不良观测工况存在，以及由于目标旋转运动引起的遮蔽问题，在观测过程中不可避免地会出现特征点丢失和测量缺失。而一旦出现这种情况，仅采用卡尔曼滤波方法只能基于系统的预测模型(状态方程)来预测系统状态，而无法基于观测值进行状态更新，从而会导致卡尔曼滤波器状态估计精度的不足。另外，对目标状态估计精度不足又会反过来使得难以重新检测到并寻回跟踪丢失的特征。针对这一问题，Oumer等[11]利用光流法和特征立体匹配来预测目标相对于观测者的速度，从而实现了存在遮蔽问题时目标的姿态和角速度恢复。但该方法依赖于光流技术，受空间光照环境影响严重，且只能通过稀疏3D点来估计部分姿态。Biondi等[7]通过立体视觉传感器跟踪目标的一些特征点，利用压缩感知和卡尔曼滤波实现对空间碎片角速率的估计。但文中仅仅给出了卡尔曼滤波过程，而直接假定了目标的特征位置的先验信息已知。Feng等[12]针对缺乏可靠的视觉特征以及对光照环境鲁棒性的需求，提出了一种新的基于卷积神经网络(CNN)的姿态确定方法，实现了对机载姿态的实时估计，摆脱了对图像特征和先验相对状态信息的依赖。但CNN的可靠训练需要大量的图像数据集和计算资源，因此必须预知目标的部分模型信息，用于合成虚拟图像并进行训练。

在观测方式方面，目前已有的针对空间目标观测的方法大多基于单个观测航天器对目标实施观测[13-14]。其中，基于单目相机对空间非合作目标的观测和导航研究已有了诸多成果。尤其在轨道导航方面，利用单目相机获得的目标测角信息，即可实现对目标相对运动信息的精确导航[15-18]，摆脱了对相对距离观测量的需求和距离测量敏感器的依赖，大大降低了航天器导航系统的能耗、体积负载和造价需求。进一步地，如果目标上存在3个及以上确定的特征点，可以利用仅测角导航方法解算目标姿态。然而，针对无合作标识点的空间翻滚目标，由于特征点信息不明确和特征跟踪丢失等问题，仅测角导航方法难以解算目标的姿态变化。同时，由于单目相机无法获得空间目标的点云信息，因此难以通过点云匹配的方式实现对空间翻滚非合作目标的姿态解算[19]。基于单一观测航天器配置的双目或多目立体视觉相机，相比于单目相机，可以得到更为丰富且高效的观测信息，例如：目标的点云信息。然而，受限于立体视觉相机的基线长度等因素，其能够实现有效测量和重建的范围有限，多应用于极近距离的空间操作需要。此外，考虑到空间光照等复杂空间环境的影响，难以保证单一航天器能够长期处于良好的观测位置。而一旦航天器观测位置不佳，基于单一观测航天器上的观测方式，其受到的观测干扰难以进行校正和消除。

考虑到空间非合作目标参数识别具有先验模型信息未知且特征点跟踪困难的特点，本文提出了基于多航天器多视点协同观测参数识别方法。该方法的主要思路是基于各观测时间帧多航天器协同观测得到的多视点视觉信息，对目标进行三维重建，进一步基于相邻时间帧之间的特征和点云匹配，解算目标的姿态变化量，并利用EKF进行滤波，实现对空间非合作目标的姿态和角速度估计。

1 多航天器协同观测及目标信息提取

1.1 问题描述

在空间环境下，非合作目标由于自身轨道姿态控制能力丧失，以及外界干扰力的作用，会在空间中自行慢速旋转。在旋转过程中，由于目标惯性主轴和旋转轴之间的耦合效应，会出现章动现象，并最终导致空间非合作目标的自由翻滚状态[20]。

目前，由于针对空间非合作目标的观测多采用基于单一航天器配置单目或多目相机的观测方式，因此鲜有采用多个航天器对单一目标进行协作观测的相关观测约束和编队控制研究。考虑到本文的研究重点为多视点协作观测可行性分析，因此仅基于空间单目观测相机的相关参数和性能对多视点观测约束进行初步分析，并以此为基础进行协作观测编队和方法设计。

1.2 基于多颗卫星编队协作的多视点观测方法

基于上述分析，以及对观测航天器轨道机动和姿态调整能力的考虑，本文提出了采用多个航天器从不同视点对空间非合作目标进行协同观测的多视点观测方法。针对空间非合作目标，划定其可能的活动空间，采用多颗卫星进行伴飞，并从中选择适当数量和位置的航天器构成观测编队对目标进行协作观测。

1) 多颗卫星协作观测约束分析

针对可能活动空间范围已知的空间非合作目标，从多颗卫星中选择合适的卫星以构成目标观测编队的约束分析如下：

①基于目标可能活动空间和相机的有效观测距离，观测航天器应处于有效观测位置。首先，受限于相机性能的限制，必然存在一个最大的有效观测距离，可以选择和单目相机同等的最大有效观测距离，例如150 m。此外，考虑到相机视场应尽可能的涵盖目标的活动区域，还存在最小有效观测距离的限制，即

(1)

式中:dmin为最小有效观测距离；Rtarget为目标活动区域尺度半径；AFov为相机视场角。

②基于目标可能活动空间和相机的有效视场，观测航天器应处于有效观测姿态。从各观测航天器出发，到目标可能活动区域中心，构成各航天器的理想观测视线，各航天器负载相机的光轴和其理想观测视线之间的夹角，应小于一定的角度阈值，以保证目标活动区域尽可能在相机视场内。

③考虑到各个视点获取的图像间相互匹配的需求，各观测航天器所负载相机的光轴之间的夹角，应处于一定的角度阈值范围之内，各观测航天器间的相对位姿应满足相应的约束。

④考虑到可能的最佳通讯距离限制，各观测航天器之间的距离应小于有效通讯距离阈值。

上述约束条件，保证了所选卫星都处于合适的观测位置和观测姿态，并可以进行协作观测。

2) 对空间非合作目标协作观测的卫星编队构型设计

采用多颗卫星编队对待辨识的空间非合作目标进行伴飞，解算各航天器和目标可能活动区域间的相对位姿关系，基于上述协作观测约束条件初步筛选出满足约束的观测航天器。若可选择的观测航天器数量不足，则基于最小燃料消耗准则，对航天器集群进行轨道机动和姿态调整，以保证足够数量的航天器满足协作观测约束条件。

解算各航天器姿轨运动状态，按照上述约束条件和判定规则，实时检索并激活满足协作观测约束条件的航天器组合，最终实现如图1所示协作观测构型。对空间非合作目标进行观测，整合时序变化的观测相机序列和获取的目标图像信息，构建关于目标的时序观测数据集。

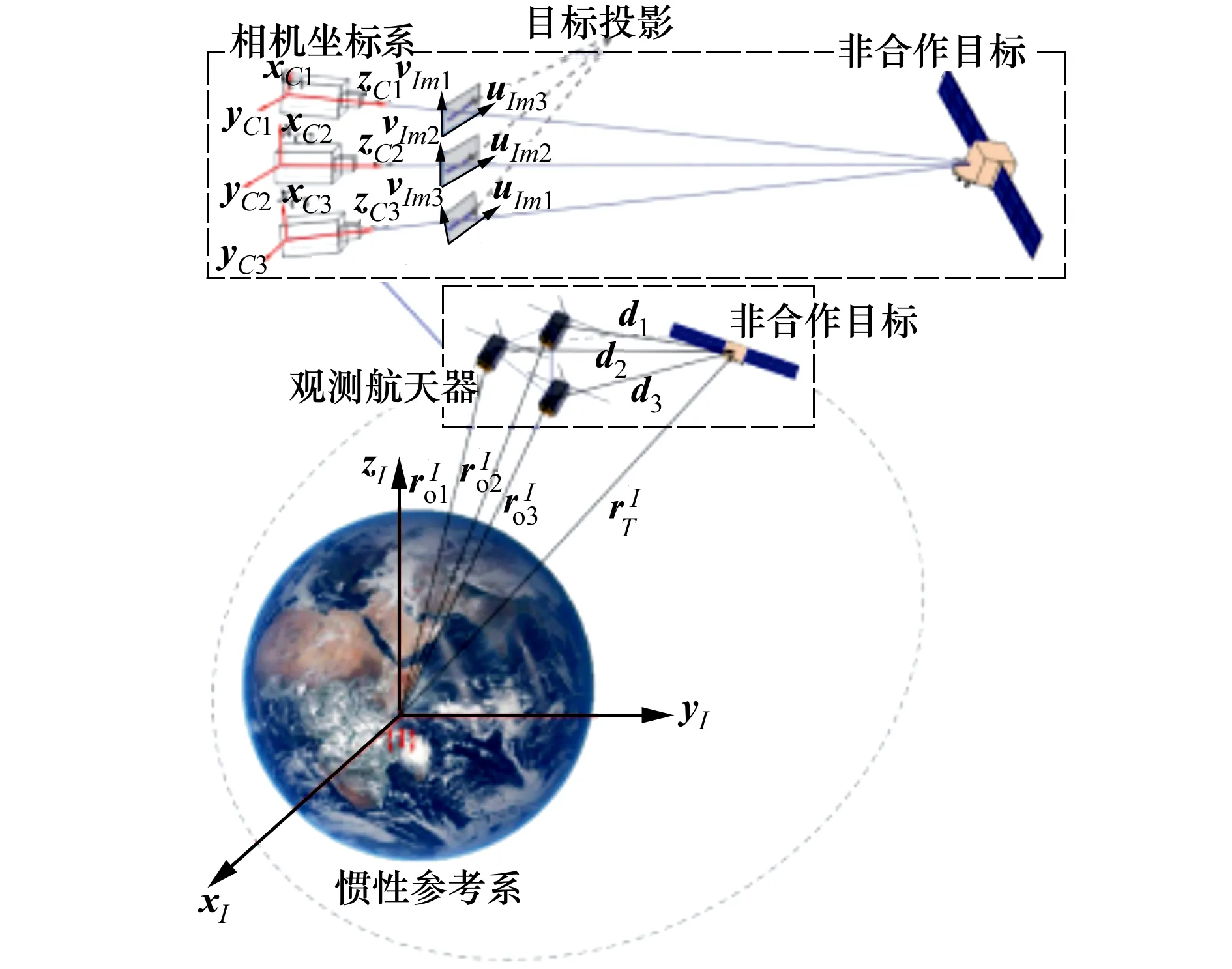
图1 针对空间非合作目标的卫星编队协作观测方案

1.3 多视点协同观测数据处理

针对协同观测获取的关于目标的协作观测数据，整个数据处理流程可分为2个部分：各时间帧上基于多视点图像的空间目标三维重建和基于时间帧间三维重建结果的目标姿态变量解算，如图2所示。

图2 基于多视点协作观测图像序列的目标姿态变量解算流程

三维重建的基本理论和原理，乃至一般的重建流程，目前都已是非常明确的，而本文为了从多视点图像序列中获取目标的帧间姿态变化量，采用了一种基于特征点的多视图重建方法，包括以下步骤：

1) 对图像数据集按时间帧进行分组，并对各时间帧的图像组分别进行特征检测和特征匹配；

2) 基于配对的特征点，结合各视图间已知的相对位姿信息，恢复各个时间帧特征点的深度信息和三维坐标信息；

3) 在前后2个时间帧的图像组间，基于已检测到的特征点进行特征点匹配；

4) 基于前后2个时间帧的图像组间配对特征点对应的空间坐标变换，解算目标的姿态变化。

1.4 基于多视图的三维重建

首先，针对各个观测视点获取的图像，选择加速稳健特征算子(speeded up robust features,SURF)[21]进行特征提取。除了特征点位置外，SURF检测器还为每个特征点赋予了一个64维的局部特征描述符，以用于图像间的特征匹配。

在图像间的特征匹配过程中,使用近似最近邻算法(ANN)进行主匹配。相机A获取的图像m中的第i个点(m)pi和相机B获取的图像n中的第j个点(n)pj的匹配判定条件设定如下:

1) 在图像n的所有特征点中,点(n)pj的描述符和点(m)pi的描述符之间的距离(如欧氏距离)最小;

考虑到协作相机间的相对位姿已知,可利用极线约束减小搜索区域,去除异常值

(2)

该公式含义为,对于在图像m上特征检测得到的一个特征点,其在另一幅图像n上的匹配视图一定在对应的极线上。式中(m)pi和(n)pj分别为图像m和n上匹配特征点的正则化坐标;F为基础矩阵,有

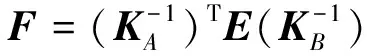
(3)

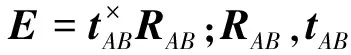
随后,基于匹配的特征和各视点相机的位姿信息,利用三角测量方法进行三维重建,得到目标的特征点云。三角测量方法的基本原理可简要描述如下:

对空间中一点,其三维坐标的齐次形式为ρ=[X,Y,Z,1]T,在相机A获得的视图m中像素齐次坐标为(m)p=((m)x,(m)y,1)T,在相机B的视图n中像素齐次坐标为(n)p=((n)x,(n)y,1)T,基于匹配的特征点(m)p和(n)p,可构建相应的方程组

(4)

式中：p×表示坐标向量p的叉乘矩阵；MA,MB分别为相机A和B的外参矩阵,表示世界坐标系在相机坐标系下的描述,有M=[R|T]。其中,世界坐标系的意义在于选择一个共用的基准坐标系来描述摄像机的位置,并用来描述观测目标的位置,在本文中,根据对空间非合作目标的观测需求,可以选择主服务航天器的轨道坐标系或本体坐标系作为世界坐标系。

不同于双目或多目相机形式的立体视觉,由于各视点间相对较远的基线距离和不同的观测姿态,无法利用基线信息简化运算。此外,考虑到基线距离较远带来的误差增大现象,选择引入多个视点来提高解算精度。当Ncam个(Ncam>2)视点获取的图像间存在匹配的特征点时,方程组(3)可随着视点数目的增加而任意扩展

(5)

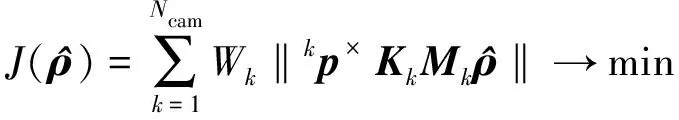
(6)

式中,Wk为相机k相应的正定加权系数,表征该视点相机的置信度权重。

记录

(7)

作为该空间点的置信度权重。

考虑到可能存在的误匹配现象,引入偏差阈值ερ,依据约束条件

(8)

去除偏差过大的空间点。

1.5 帧间目标姿态变量确定

首先,在前后2个时间帧的图像组间,基于1.4节中检测到的特征点进行特征匹配。依次选择各个相机作为主相机,使用近似最近邻算法进行主匹配,匹配判定条件设定为:

1) 满足主相机前后2个时间帧获取的图像间的特征点匹配判定条件,即如1.4节所述;

2) 和主相机视图特征点对应的辅助相机不同时间帧图像上的特征点间同样要满足匹配判定条件。

基于匹配的特征点,构建出随着时间帧变化的3D特征点云,整合各个相机作为主相机获得的空间点云序列,并更新各相机的权重

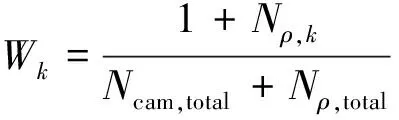
(9)

式中:Nρ,k为相机k作为主相机时获得的空间点总数;Nρ,total为最终获得的空间点总数;Ncam,total为参与观测的相机总数。

随后,考虑到空间点云中可能存在的重复和邻近现象,引入邻近判定条件

i≠ji,j=1,2,…,Nρ,total

(10)

依据空间点的置信度去除临近空间点中置信度相对较低的点,以避免出现病态现象。

空间点云在前后2个时间帧的变化可描述为RT变换形式,即

(11)

(12)

(13)

2 扩展卡尔曼滤波技术

扩展卡尔曼滤波(EKF)是标准卡尔曼滤波在非线性情形下的一种扩展形式,作为一种高效率的递归滤波器,在空间目标运动学和动力学参数估计中有着广泛的应用。

对于包含待估计参数量的状态向量x,其估计模型即状态转移方程为

xk=f(xk-1)+sk

(14)

测量模型即观测方程为

zk=h(xk)+vk

(15)

基于估计模型和测量模型,EKF对状态量的估计和更新流程如下:

估计(传播):

(16)

(17)

更新(校正)

(18)

(19)

(20)

(21)

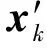
(22)

2.1 估计模型

状态向量定义为

x=[qT,ωT]T

(23)

式中,q为目标的姿态四元数,其定义为

q=[q0,q1,q2,q3]T=

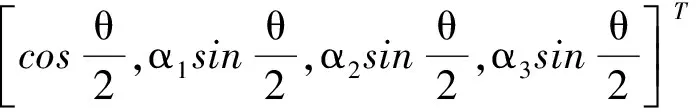
(24)

式中,α1,α2,α3为表征旋转轴的单位向量的分量,θ为旋转角度。四元数形式的运动学方程为

(25)

式中

(26)

ω=[ω1,ω2,ω3]T表示目标航天器的角速度,不考虑外力矩影响,其动力学方程为

(27)

式中:J为目标的惯量张量阵;ω×表示ω的叉乘矩阵。

2.2 测量模型

假定Pi为空间目标上的特征点,ρi为其在视觉参考系中相应的坐标向量,即

ρi=ρ0+D(q)Pi

(28)

式中:ρ0为目标质心的相对位置坐标;D(q)为目标本体坐标系相对于观测坐标系的坐标变换矩阵,即目标的姿态矩阵。

考虑到空间目标的非合作性,即缺乏合作标识,特征点在目标本体坐标系中的位置可能是未知的,然而,通过1.4节中的多视点三维重建,特征点在观测空间中的坐标是可知的。出于这一考虑,选择前后2个不同时间帧同一特征点Pi在观测坐标系中的坐标表达式构建方程组

(29)

消去Pi,整理可得

(30)

式中,ΔΦ表示目标的姿态变化矩阵,有

ΔΦ=D(qt+Δt)D-1(qt)=D(Δq)

(31)

式中,Δq为姿态四元数变量,有

Δqqt=qt+Δt

(32)

显然,通过前后不同时间帧中同一组特征点在观测坐标系中的位置坐标,即目标的点云信息,计算目标的姿态变化量,并以此构建观测量,可以避免特征点在目标本体坐标系中坐标未知或存在不确定性的问题。

3 仿真分析

3.1 航天器协同观测编队构型设计

选择风云一号模型作为参考,建立相应的仿真几何模型,如图3所示。假定光照环境良好,并忽略卫星的外表材料等因素可能导致的过曝现象,以图4为例,本文的协同观测方式设计如下:

图3 参考风云一号的目标仿真模型

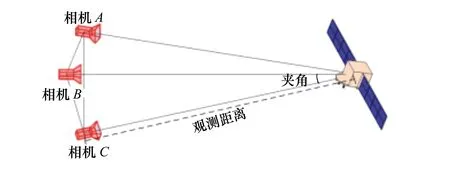
图4 基于三视点的协同观测方案

多颗观测卫星上分别安装一个CCD相机,从不同位置和角度对目标进行观测,虽然更多的视点可以获得更为优良的结果,但本文出于简化问题以便于模拟仿真的考虑,仅选择3个视点进行协同观测,并同双视点协同观测进行对照,而后续的仿真结果也表明,3个视点的协同观测已经可以一定程度地满足精度需要。基于同样的考虑,虽然在实际观测工况中,各个视点相对于目标的距离和观测角度不可避免地存在差异和波动,本文在模拟仿真中为简化问题,假定3个相机视点构成一个正三角形,各个相机均始终正对目标,且和目标的距离一致,即目标和3个视点构成一个正三棱锥。通过调节观测距离和视线夹角(即各相机光轴之间的夹角),对相机位置和姿态进行一致性的确定和调整:基于设定的观测距离和观测视线夹角确定虚拟相机的观测位置,然后,考虑相机视线固定指向目标模型,确定虚拟相机的观测姿态。设定目标模型的初始姿态和姿态变化量,通过各个虚拟相机获取相应的映射图像,构成姿态随时间变化的图像序列集。

3.2 协同观测构型设计及优化

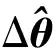
(33)

统计蒙特卡洛打靶结果,其结果如图5和图6所示,分别为基于2个和3个相机视点在不同观测距离和相机视线夹角下的目标姿态角的观测误差。

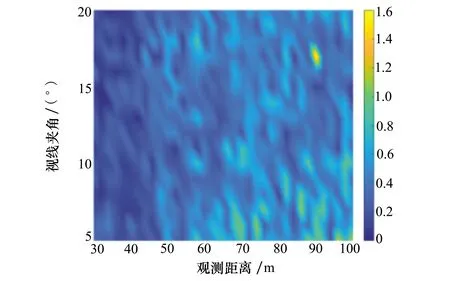
图5 基于双视点观测的姿态角解算误差

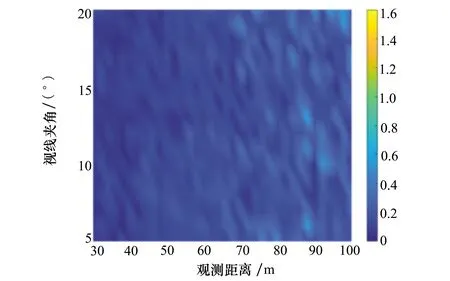
图6 基于三视点观测的姿态角解算误差

其中横轴表示观测距离,纵轴表示各视点间的视线夹角,通过协同观测解算得到的平均姿态角变量和设定姿态变量之间的误差以0°～1.6°区间变化的色度表示。可以看到,当使用双视点对目标进行观测时,其解算的姿态变量相对于设定的姿态变量存在着较大的误差,仅当观测距离十分接近时,绝对误差在0.2°左右,而随着观测距离的拉远,其绝对误差普遍在0.6°左右,甚至存在超过1°的绝对误差波动。相比而言,使用三视点对目标进行协同观测的表现良好,其在距离较近时的解算误差要小于0.2°,而且大多情况下解算精度都能保持在0.2°左右,仅在距离较远时出现了少量的0.6°左右的误差结果。两者对比表明,仅使用双视点对目标进行协同观测,解算得到目标姿态变量存在较大的误差,可能无法满足对目标观测和参数识别的需要；使用三视点对目标进行协同观测,不论是姿态变量解算的精度,还是稳定性,都有了大幅度的提高,后续的滤波结果也证明其满足了参数识别所需。

这是由于,当使用双视点的相机进行观测时,其仅能实现对深度信息的解算,而一旦出现匹配误差较大乃至误匹配的现象,即会造成深度信息解算错误。此时,由于缺乏源于第三方观测的校正,观测系统无法实现对误匹配的消除和修正,导致最终的观测结果会存在较大的错误。而3个视点协同观测的方式,通过彼此间的相互校正,最终可以获得更好的观测精度。

3.3 多视角信息融合的EKF仿真结果分析

目标初始姿态和角速度设定为

q0=[1,0,0,0]T

ω0=[5,5,5]T°/s

(34)

滤波器的初始条件根据高斯分布给出,即

(35)

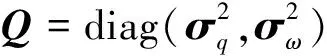
选择姿态四元数作为观测量,基于姿态角解算结果中的姿态角解算误差,在姿态四元数中添加测量噪声R来构建观测数据,测量噪声R设定为零均值高斯白噪声,模拟表示多视点协同观测姿态角解算误差,其协方差矩阵根据多视点协同观测结果,利用UT法[22]演算求得。

根据如图5和图6所示的姿态角观测解算误差分布,对应基于3个视点和2个视点进行协同观测的普遍绝对误差,选择姿态角观测误差为 0.2°和0.6°的2种工况,分别进行EKF滤波。相应的EKF滤波结果如图7和图8所示。

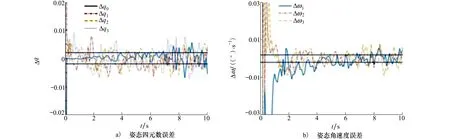
图7 协同观测姿态角解算误差为0.2°的EKF滤波结果 图8 协同观测姿态角解算误差为0.6°的EKF滤波结果

可以看到,当协同观测姿态角解算误差设定为0.2°时,可以取得相对良好的收敛结果,无论是姿态四元数误差的4个分量,还是角速度误差的3个分量,都可以快速收敛到指定阈值内。而当协同观测姿态角解算误差设定为0.6°时,系统表现出了无法收敛的现象,姿态四元数误差和角速度误差的波动范围普遍地超出了设定的阈值范围。

选用蒙特卡洛打靶法进行进一步的分析和证明,定义姿态误差为

(36)

角速度误差定义为

(37)

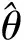
首先，针对随机的滤波初始条件进行蒙特卡洛打靶。由于滤波的初始条件是高斯分布给出的，而其又对滤波过程和滤波结果有着重要的影响，因此，单次的滤波仿真不足以进行收敛性的证明和判定。针对2个不同的姿态角(0.2°和0.6°)观测解算误差，进行100次蒙特卡洛打靶实验。如图9和图10所示为其中的10次典型结果。

图9 协同观测姿态角解算误差为0.2°的蒙特卡洛结果

图10 协同观测姿态角解算误差为0.6°的蒙特卡洛结果

可以看到，当协同观测姿态角解算误差设定为0.2°时，可以取得良好的收敛结果，基于不同初始条件的多次滤波结果，无论是姿态误差，还是角速度误差，都可以快速的收敛到指定阈值内。而当协同观测姿态角解算误差设定为0.6°时，系统表现出了收敛不稳定和难以收敛的现象，大多初始条件的姿态误差和角速度误差都无法收敛到指定阈值范围之内。

进一步地，针对不同的协同观测姿态角解算误差进行蒙特卡洛打靶。协同观测的仿真结果表明，不同观测距离和观测视线夹角下的观测解算误差存在差异和波动。本文选定观测距离40～80 m，观测视线夹角10°～15°的观测区间，参照图5和图6所示的观测解算误差，对应的2个视点和3个视点的观测姿态角解算误差范围分别为0.03°～0.85°(双视点)和0.025°～0.35°(三视点)，分别进行100次蒙特卡洛打靶实验。如图11和图12为其中的10次典型结果。

图11 对应三视点观测的观测姿态角解算误差范围为0.025°～0.35°的蒙特卡洛结果

图12 对应双视点观测的观测姿态角解算误差范围为0.03°～0.85°的蒙特卡洛结果

可以看到，在观测距离40～80 m，观测视线夹角10°～15°的这样一个观测区间内，当选择三视点进行协同观测时，其姿态角观测解算误差范围为0.025°～0.35°，在此区间内的EKF滤波大多可以取得良好的收敛结果，蒙特卡洛打靶结果表明，无论是姿态误差，还是角速度误差，大多可以收敛到指定阈值内，仅存在少量的超出阈值的现象。而当选择双视点进行协同观测时，其观测解算误差解算误差范围为0.03°～0.85°，在此区间的EKF收敛性能不足，蒙特卡洛打靶表明，虽然存在少量的收敛情况，但大多情况下，姿态误差和角速度误差都无法收敛到指定阈值范围之内。

4 结 论

针对几何外形和运动参数等先验信息未知的空间非合作目标参数识别问题，本文提出了一种基于多航天器协作观测的空间非合作目标姿态参数在轨识别方法。首先，基于同时观测获取的多视点图像序列，对目标进行三维重建。其次，根据不同观测时间帧的目标特征点云匹配，解算目标的姿态变化量，并利用EKF滤波技术对目标姿态运动信息进行估计。该方法的优点在于：其一，不用借助任何空间目标本体的标识点，仅通过多个航天器编队协同，从多视点观测目标，并基于信息融合算法估算目标姿态参数。其二，不同于单目相机或多目立体相机识别，本文提出的方法可以通过改变航天器之间的位置来调整观测视场，可以适用于各种距离不同大小的空间目标参数识别。仿真结果表明，相比于2个航天器协同观测识别目标参数，3个航天器协同观测可以得到更为精确的识别精度。通过3个航天器协同观测，以及对编队构型的优化，可以在不需要目标的任何先验信息的前提下估算出空间非合作目标姿态参数。