指数型阻尼模型复模态更新及阻尼矩阵识别

汪梦甫　肖诗颖

摘   要：提出了在模態测试的基础上识别得到指数型非粘滞阻尼系统中阻尼系数矩阵的方法. 通过求解一个带约束最优化问题，得到满足系统特征方程的最优修正阻尼系数矩阵. 考虑了实际模态测试中得到的模态参数的非完备性，可以利用有限的低阶模态，较为准确地识别出系统的阻尼系数矩阵，但随着系统的非粘滞阻尼特性逐渐增强时，想要精确识别出阻尼系数矩阵所需要的模态数目会逐渐增加. 同时，进一步考虑到模态测试中复模态的虚部受噪声影响较大，提出了阻尼矩阵识别过程中对复模态虚部进行更新的方法，使之满足指数型阻尼系统特征方程，且利用上述方法得到的复模态虚部，能较为精确地识别出阻尼系数矩阵. 由于目前对松弛因子识别的研究较少，在模态更新方法的基础上提出了不依赖于复模态虚部的松弛因子识别公式，并通过数值算例，验证了指数型非粘滞阻尼模型的阻尼识别方法及复模态更新方法的适用性和有效性，及松弛因子识别的准确性. 最后通过悬臂梁的振动测试进行模态参数识别，并讨论了指数阻尼模型的适用性和合理性.

关键词：粘弹性;复模态分析;阻尼系数;参数识别;拉普拉斯域

中图分类号：TU311                                     文献标志码：A

Complex Modal Updating and Damping Matrix Recognition

of Exponentially Damping Systems

WANG Mengfu?，XIAO Shiying

（College of Civil Engineering，Hunan University，Changsha 410082，China）

Abstract：A method of identifying damping coefficient matrix in exponential non-viscous damping systems based on the modal test is proposed in this paper. By solving a constrained optimization problem，the optimal modified damping coefficient matrix satisfying the system characteristic equation is obtained;and considering the incompleteness of the modal parameters obtained in the actual mode test，the damping coefficient matrix of the system can be accurately identified by using the limited low-order modes. However，with the gradual enhancement of the non-viscous characteristics of the system，the number of modes needed to accurately identify the damping coefficient matrix gradually increases. Furthermore，a method of updating the imaginary part of the complex mode，which can be greatly affected by noise in the modal test，is proposed to satisfy the characteristic equation of the exponentially damping system in this paper;and as a result，the damping coefficient matrix can be accurately identified by using the updated complex-modal imaginary part. Due to the lack of research on the recognition of the relaxation parameter，an identification method of relaxation parameter which is independent of the imaginary part of complex mode is proposed based on the modal updating method. And then，through numerical studies，the applicability and effectiveness of the damping identification method and the complex modal correction method for the exponentially non-viscous damping model are verified，and the accuracy of relaxation factor recognition method is proved. Finally，the modal parameters of a cantilever beam are identified through the vibration test，and the applicability and rationality of the exponential damping model are discussed.

Key words：viscoelasticity;complex modal analysis;damping coefficients;parameter identification;Laplace domain

实际工程中振动的发生通常不可避免，因此研究者们广泛关注于如何通过结构耗能（即阻尼）来进行结构减振. 但阻尼不能直接测量得到，而是根据假设的阻尼模型在宏观上近似地表达，因此对阻尼模型的假设很大程度上影响着结构动力分析的准确性和可靠性[1].  由于经典粘滞阻尼模型自身存在不足，为了满足工程界日益复杂的工程材料和结构的需要，研究者们近年来提出了一些新的阻尼模型，最早由Biot[2]提出的卷积型非粘滞阻尼模型就是其中的一种. 该模型假设阻尼力不仅依赖于瞬时速度，而且与速度的时间历程相关，数学表述为质点速度与核函数的卷积[3]. 在Woodhouse、Adhikari等人[4-5]的进一步发展下，卷积型非粘滞阻尼模型多年来得到了不同领域动力分析的研究和应用. 其中，作为卷积型阻尼模型的一个特例，指数阻尼模型在数学计算上较为简单，且能够更加合理地表述阻尼的物理本质，因此本文选择对指数阻尼模型进行研究.

结构系统的参数识别作为现代结构动力学问题的反问题之一，可以根据模态试验并结合理论分析来处理实际工程中的振动问题[6-8]. 然而此过程中，对阻尼矩阵的预估是难点，并且通常结构阻尼值由经验确定，并假定结构各阶模态阻尼比相同，这与实际情况不符[8]，因此有必要对结构阻尼的识别进行研究. 但目前的阻尼识别方法一般针对粘滞阻尼模型，对非粘滞阻尼模型阻尼识别的研究较少，国内外主要有如下研究：Adhikari等[9]根据一阶摄动法，率先将复模态分析法扩展到了指数型非粘滞阻尼模型的识别中去，然而该方法对模态参数识别的精度要求较高，且识别阻尼矩阵需要用到全模态;潘玉华[10]在

Rayleigh阻尼模型的基础上，提出了指数型比例阻尼模型，假设指数阻尼核函数的阻尼系数矩阵具有和Rayleigh阻尼相对应的形式，并给出了相应松弛因子的迭代计算方法;王禹[11]将阻尼矩阵分解法拓展到指数型非粘滞阻尼模型中，识别该模型的阻尼系数矩阵，该方法能够在只获得低阶模态信息的情况下较为准确地识别出阻尼系数矩阵.

在结构参数识别过程中，通常需要依据一部分有限元模型分析值来识别所需要的真实值，但往往有限元理论分析结果与试验测量结果存在差异，因此可以依据试验结果对分析模型进行更新，使得更新后的模型能更加精确地反应结构的动力响应[12]，从而提高结构参数识别的准确性.

基于以上研究背景，本文研究了在模态测试的基础上对指数型阻尼模型中进行阻尼系数矩阵识别及复模态更新的方法，并在此基础上提出了新的松弛因子识别公式.

4   数值算例分析

4.1   案例1：模态参数精确时识别阻尼系数矩阵

为了验证本文提出的阻尼识别方法的适用性和有效性，利用文献[11]中的7自由度系统进行模拟计算. 该系统质量矩阵、刚度矩阵和阻尼系数矩阵真实值分别为：

其中，μ为松弛因子. 假定分析阻尼系数矩阵CA = 0，权矩阵取为WC = diag（1  1   1   1   1   1  1），运用式（28）识别指数型阻尼系數矩阵C. 松弛因子μ可被表示为[16]：

μ =               （67）

式中：Tmin表示最高阶无阻尼固有频率所对应的周期，这样结构的阻尼机制可以由γ的取值来控制，γ越小，阻尼机制就越接近于粘滞阻尼[16]. 下面分别取γ=0.002、0.2、2三种情况识别阻尼系数矩阵，具体阻尼系数识别值见表 1，表1中仅给出了阻尼系数矩阵对角线上的值的大小.

从表1中可看出，本文提出的方法能较好地识别出阻尼系数矩阵，但随着γ的增大，系统的非粘滞阻尼特性逐渐增强时，想要精确识别出阻尼系数矩阵所需要的模态数目逐渐增加;当γ增加到2时，需要取得全模态才能精确识别出阻尼系数矩阵.

当γ取值较大时，对阻尼系数矩阵识别误差较大且所需模态数较多的原因，认为和文中识别公式（28）中的广义逆矩阵（W 1/2

C   ψ）+有关. 通过MATLAB多次计算可以发现，当γ值增大，矩阵ψ的条件数也逐渐增大，求广义逆矩阵时精度难以提高，从而误差变大. γ值一定时，随着选取的模态阶数增加，矩阵ψ的条件数减小，从而精度越高.

按文献[11]的识别方法对阻尼系数矩阵进行识别的结果见表2. 表2中给出的是能较为精确地得到阻尼系数矩阵所需的最小模态阶数，以及在该模态阶数下的阻尼矩阵识别情况. 将表1与表2的结果进行比较，可以看出，在不同的取值以及不同的模态阶数下，文献[11]方法的识别精度均要高于本文的识别方法.

取文献[17]中含指数阻尼的轴向振动悬臂杆模型作为算例，分析两种方法在对不同自由度下阻尼矩阵进行识别的耗时情况. 该悬臂杆模型如图1所示.

该悬臂杆单元质量矩阵和单元刚度矩阵分别为：

本文中该悬臂杆参数取为：ρ = 7.8 × 103 kg/m3为杆件密度;A = 6.25 × 10-4 m2为杆件截面面积;E = 2.1 × 1011 N/m3为弹性模量;L = 4 m为杆长;Le = L/n为每个杆单元的长度;n为悬臂杆划分的单元数目. 系统的阻尼系数矩阵设为C = α0 M + α1 K，其中系数 α0 和α1取为：

α0  = 2ξ，α1  = 2ξ

式中：阻尼比ξ取0.05，第j阶无阻尼固有频率为ωj = π. 松弛因子μ按式（67）计算，其中γ取为1.

分别取n=10、20、40和80四种情况，按本文提出的方法和文献[11]的识别方法取全模态识别阻尼系数矩阵C所需要的时间见表3. 从表3中可以看出，由于文献[11]的识别过程涉及了大量的循环运算，若结构的自由度数较多，在利用MATLAB进行求解时会耗时较长;在本文的方法中，结构的自由度取值对运算时间影响相对而言不大. 因此，在自由度较少的情况下，利用文献[11]提出的阻尼系数矩阵识别方法可以得到更好的结果;在结构自由度数较多时，如果有运算时间上的需求，采用本文提出的方法则更有效率.

4.2   案例2：复模态虚部更新后识别阻尼系数矩阵

取案例1中的7自由度系统作为算例进行分析，取γ=0.02. 现给复模态虚部添加均值为0、标准差为0.1%的噪声，复模态实部取为精确值，更新前阻尼矩阵的识别情况见表4.从表4中可以发现，只有取全模态进行识别时，才能得到较为准确的阻尼系数矩阵，但仍不是精确值;若取的模态值不全，即使是前六阶，在该噪声下的结果仍完全失真，数据失效显著. 可以看出复模态虚部的准确度对识别结果能造成影响.

按本文提出的复模态更新方法，对复模态虚部值进行更新后，識别得到的阻尼系数矩阵对角线上数值见表5. 从表5中可看出，在对复模态虚部进行更新后，精确识别出阻尼系数矩阵所需要的模态数目增加了，取得全模态便能精确识别出指数阻尼系数矩阵;对复模态进行更新后可以排除噪声对复模态虚部的干扰，反映出本文提出的复模态虚部计算公式（52）能满足阻尼矩阵识别的需要.

4.3   案例3：对松弛因子的识别

取案例1中的7自由度系统研究松弛因子识别式（64）～（66）的准确性. 当γ值较小时，如γ=0.002，该系统更接近于粘滞阻尼系统，按不同方式识别得到的γ值见图2. 从图2中可以看出，这3种识别公式均能较好地识别出松弛因子，按式（65）（66）获得的松弛因子更接近原始值.

当γ值较大时，如γ=2，此时该体系的阻尼机制表现为明显的非粘滞阻尼特性，按不同方式识别得到的γ值见图3.从图3中可以看出，这3种识别公式也均能较好地识别出松弛因子，按式（65）获得的松弛因子更接近原始值.

5   试验分析

本小节将对一根混凝土悬臂梁构件进行锤击振动测试试验，对本文提出的阻尼系数矩阵方法进行研究，并讨论指数阻尼模型的适用性.

5.1   试验概况

该悬臂梁试件配筋和尺寸信息如图4所示. 试件采用C35普通混凝土，水泥采用42.5级普通硅酸盐水泥. 纵筋采用HRB400级钢筋，抗拉强度设计值为360 MPa，弹性模量为200 GPa;箍筋采用HPB300级光圆钢筋，抗拉强度设计值为270 MPa.

该试件的参数为：密度ρ=2.41×103 kg/m3，截面积A=0.04 m2，弹性模量E=3.06×1010 N/m2，梁长L=0.2 m.

振动试验数据采集设备采用比利时公司的LMS锤击测振系统. 振动测试前，将悬臂梁沿梁身均匀取10个锤击作用点，并在顶部粘贴加速度传感器. 锤击法振动测试试验示意图见图5. 测试时，用力锤依次对所标记的10个测点进行锤击，利用数据采集仪记录下每次锤击时的力传感器信号及加速度响应信号，并计算得到每个锤击点的频响函数平均值. 本章的试验完成于湖南大学结构实验室.

利用试件实测频响函数曲线，在LMS.Test.Lab软件上进行分析，使用最小二乘复指数法 （LSCE） 可以估计出试件的频率、阻尼比，并可以计算出相应模态振型.

5.2   结构阻尼系数识别

首先将该试件质量矩阵与刚度矩阵按有限元法进行建模，只研究试件振动方向上的平动自由度，可以得到所需的质量矩阵和刚度矩阵分析值，均为10×10方阵. 按照文献[18]提出的迭代算法，对分析质量矩阵与分析刚度矩阵进行修正，可得该试件修正后的质量矩阵M和刚度矩阵K. 利用识别得到的前五阶模态参数及修正后的质量矩阵M和刚度矩阵K识别松弛因子μ. 按公式（65）计算得到的μ=145.868 s-1.

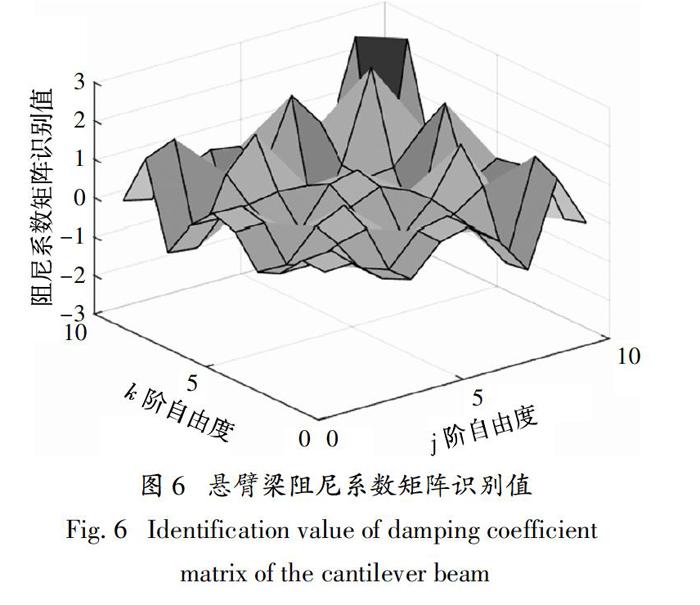
接下来按本文提出的复模态更新方法对该试验梁进行复模态虚部的更新，并进行指数阻尼系数矩阵识别，识别得到的阻尼系数矩阵如图6所示. 由图6可以看出，该识别出的阻尼矩阵的阻尼系数分布不是很明显，可能与试验模态测量误差有关.

悬臂梁试件的前三阶固有频率及阻尼比分别按指数型非粘滞阻尼模型和Rayleigh阻尼模型的识别结果见表6.

从表6中可以看出，通过文中提出的方法按这两种阻尼模型识别的固有频率均接近试验实测值，但识别得到的阻尼比与实测值有差别. 试验测量得到的阻尼比为按单模态识别得到的各测点的每阶模态平均值，而按这两种阻尼模型识别得到的阻尼比为按整体模态计算分析的结果，从而带来识别误差. 与按指数阻尼模型计算得到的阻尼比相比，该试验梁采用Rayleigh阻尼模型计算出的第三阶阻尼比与试验实测值相差较大，远大于实测值，这种误差能显著影响结构的动力特性. 指数阻尼模型由于参数松弛因子的存在，可以更为合理地拟合结构的阻尼特性.

6   结   论

1）本文提出了指数阻尼系统中对阻尼系数矩阵识别的方法，通过求解一个带约束的优化问题，利用权函数矩阵及初始分析阻尼矩阵，获得满足系统特征方程的阻尼系数矩阵;该方法不需要测得全模态，可以获得比较高的识别精度，但随着系统的非粘滞阻尼特性逐渐增强时，想要精确识别出阻尼系数矩阵所需要的模态数目会逐渐增加;当非粘滞阻尼特性足够大时，最后可能需要取得全模态才能精确识别出阻尼系数矩阵.

2）针对试验噪声对测量得到的复模态虚部精度的影响，本文提出了对复模态虚部进行更新的方法，使之满足指数型阻尼系统特征方程;通过算例分析，将更新前后识别得到的阻尼系数矩阵进行对比，可以看出，提出的阻尼系数矩阵识别公式对噪声较为敏感，且复模态虚部的准确度对阻尼矩阵识别结果影响较大;采用更新后的复模态虚部表达式可以排除阻尼矩阵识别过程中噪声对复模态虚部的影响，且能有效地识别出阻尼系数矩阵;但在对复模态进行更新后，在相同模态阶数下对阻尼系数矩阵的识别精度降低了，并且精确识别所需的模态阶数较多，不使用全模态时识别精度较差，目前的更新方法可以进一步改进.

3）由于目前对松弛因子识别方法的研究较少，且有一定使用限制，本文提出了不依赖于复模态虚部的3种松弛因子识别公式，通过算例分析表明这3种公式均能较高精度地识别出松弛因子，能够满足结构分析的需要.

4）通过对普通C35混凝土悬臂梁进行锤击振动测试，并按本文提出的方法进行模态参数识别，将采用Rayleigh阻尼模型和本文采用的指数型非粘滞阻尼模型识别得到的阻尼比和基本频率进行对比，可发现识别得到的固有频率接近试验实测值，但阻尼比与实测值有差别，采用Rayleigh阻尼模型时第三阶阻尼比出现了很大的误差. 指数阻尼模型更能准确合理地描述两根混凝土悬臂梁的阻尼性能.

参考文献

[1]    李劍清. 用随机衰减法评估建筑结构的阻尼[D].  武汉：华中科技大学，2003：1—15.

LI J Q. Estimating the damping of building structures by random decrement technique[D].  Wuhan：Huazhong University of Science and Technology，2003：1—15. （In Chinese）

[2]    BIOT M A. Variational principles in irreversible thermodynamics with application to viscoelasticity[J].  Physical Review，1955，97（6）：1463—1469.

[3]    WAGNER N，ADHIKARI S. Symmetric state-space method for a class of nonviscously damped systems[J].  AIAA Journal，2003，41（5）：951—956.

[4]    WOODHOUSE J. Linear damping models for structural vibration[J].  Journal of Sound and Vibration，1998，215（3）：547—569.

[5]    ADHIKARI S. Dynamics of nonviscously damped linear systems[J].  Journal of Engineering Mechanics，2002，128（3）：328—339.

[6]    赵艳，潘嘉宁，王振宇，等. 风力机启停机过程中的振动特征分析[J].  湖南大学学报（自然科学版），2019，46（3）：82—89.

ZHAO Y，PAN J N，WANG Z Y，et al. Analysis of wind turbine vibration characteristics during startup and shutdown process[J].  Journal of Hunan University （Natural Sciences），2019，46（3）：82—89. （In Chinese）

[7]    陈桂平，文桂林，崔中，等. 高速磨床主轴模态测试与分析研究[J].  湖南大学学报（自然科学版），2010，37（4）：22—26.

CHEN G P，WEN G L，CUI Z，et al. Modal testing and analysis of the main shaft for high-speed grinder[J].  Journal of Hunan University （Natural Sciences），2010，37（4）：22—26. （In Chinese）

[8]    林凡伟. 轻木-混凝土混合结构振动台试验阻尼识别研究[D].  上海：同济大学，2008：1—8.

LIN F W. Research on damping identifying of shake table test for wood-concrete hybrid structure[D].  Shanghai：Tongji University，2008：1—8. （In Chinese）

[9]    ADHIKARI S，WAGNER N. Analysis of asymmetric nonviscously damped linear dynamic systems[J].  Journal of Applied Mechanics，2003，70（6）：885—893.

[10]  潘玉华. 指数型阻尼模型及其在钢筋混凝土结构动力分析中的应用[D].  北京：北京交通大学，2013：78—99.

PAN Y H. Exponential damping model and its applications to dynamic analysis of reinforced concrete structures[D].  Beijing：Beijing Jiaotong University，2013：78—99. （In Chinese）

[11]  王禹. 指数型非粘滞阻尼模型参数识别的理论与试验研究[D].  哈尔滨：哈尔滨工业大学，2017：8—37.

WANG Y. Theoretical and experimental research on parameter identification of exponential non- viscous damping model[D].  Harbin：Harbin Institute of Technology，2017：8—37. （In Chinese）

[12]  蒋家尚，袁永新. 基于复模态实验数据的粘性阻尼矩阵的修正[J].  振动与冲击，2007，26（5）：74—76.

JIANG J S，YUAN Y X. Updating of viscous damping matrix based on incomplete complex modal data measured[J].  Journal of Vibration and Shock，2007，26（5）：74—76. （In Chinese）

[13]  孔翠芳，戴华. 用不完全模态试验数据修正粘性阻尼矩阵[J].  振动工程学报，2005，18（1）：85—90.

KONG C F，DAI H. Updating of the viscous damping matrix from incomplete modal experimental data[J].  Journal of Vibration Engineering，2005，18（1）：85—90. （In Chinese）

[14]  HALEVI Y，KENIGSBUCH R. Model updating of the complex modeshapes and the damping matrix[J].  Inverse Problems in Engineering，2000，8（2）：143—162.

[15]  ADHIKARI S. Damping models for structural vibration[D].  Cambridge：University of Cambridge，2000：61—183.

[16]  沈洪宇. 卷积型阻尼模型参数识别与结构响应的理论与试验研究[D].  哈尔滨：哈尔滨工业大学，2010：34—40.

SHEN H Y. Theoretical and experimental research on parameter identification and time-history analysis of a convolutionary damped system[D].  Harbin：Harbin Institute of Technology，2010：34—40. （In Chinese）

[17]  ADHIKARI S，WAGNER N. Direct time-domain integration method for exponentially damped linear systems[J].  Computers & Structures，2004，82（29/30）：2453—2461.

[18]  刘皞，李超. 用自由度不完整的振型數据修正质量矩阵与刚度矩阵[J].  应用数学与计算数学学报，2012，26（4）：472—480.

LIU H，LI C. Update mass and stiffness matrices using incomplete measured modal data[J].  Communication on Applied Mathematics and Computation，2012，26（4）：472—480. （In Chinese）