二维造流水槽整流装置数值模拟

马 暄，白志刚

（天津大学 建筑工程学院，天津 300350）

1 研究背景

波流水槽是港口、水利和海洋船舶工程及相关学科的重要实验设备。为兼具造流、造波的功能，常见的波流水槽一般采用上部造波，下部造流的结构形式。由于造流廊道出入口处流态复杂，可供用于物模实验的理想区域仅限于水槽中部，有效试验段长度只有50%左右。为了尽可能增加试验段，实验室建设中常采用加大水槽长度和缩短实验区长度的方法保证实验结果的有效性，但前者加大了建设投资，后者则降低了实验精度。为了改善水槽出入口处的流态，实验中常采用盲沟材料作为整流装置。Tollmien等［1］于1961年首次提出了采用整流网改善流场品质的方法。Corrsin［2］在物理模型实验中验证了Tollmien的设想。Laws E M［3］等以金属丝-纱网为例，研究了整流网对时均流速和湍流分布的影响。

盲沟材料虽然广泛应用于实验水槽，但盲沟材料的孔隙率，整流段的长度等参数并没有明确的标准，实际建设中常依赖经验确定。建立相应的数学模型有助于确定盲沟整流装置对流场的作用效果。由于盲沟材料结构复杂，建模难度大。且水流流经盲沟材料时流态较为复杂，流态分布难以模拟。对于盲沟材料的数学模型的研究尚不充分，具有一定的研究价值。

SPH方法在大变形流体问题的模拟当中具有很好的自适应性［4］。在流速边界模拟方面，本文采用由Federico等［5］提出的周期性边界法，通过将水槽末端的粒子转移到水槽前端，实现粒子的循环流动。该方法可以保证模拟区域内粒子总数恒定不变，模拟过程中不需要创建新的水粒子。在阻尼区域的处理方面，数值阻尼法是SPH方法中常用的边界处理方法。其主要原理是通过在部分区域逐渐增加黏性，从而降低质点速度。该方法原本主要用于消除波浪模拟中的反射波［6］。本文通过修改数值阻尼区域，将其应用在造流模拟中。基于Owen等的整流理论，用数值阻尼区域的宏观特性表征实际筛网材料的微观特性，调节水流流速分布，达到实际整流装置的效果。通过与物理模型实验相对比，数值阻尼区域的整流效果与物理模型实验结果偏差在10%以内，具有较好的真实性和有效性。

2 水槽数值模拟方法

2.1 SPH方法简介 SPH是一种无网格的拉格朗日方法，在大变形流体和自由表面流体的数值模拟方面优于欧拉方法。SPH方法的基本方程是拉格朗日形式的动量方程：

式中：v为质点速度；ρ为质点密度；P为作用在质点上的压力的合力；g为重力加速度；Γ为包括黏性力、切应力等在内的耗散项的总和。针对不同的问题，可以对Γ做不同的处理。每个计算时间步中，通过式（1）得到每个粒子的加速度，从而计算出粒子的位移。计算域中所有的粒子都会参与计算，对于流体粒子，计算出的位移即为下一个时间步粒子的新位置；而对于边界粒子，计算出的位移会在时间步内清零，即视为刚性边界。

粒子密度ρ通过式（2）计算。对于粒子a来说，近似认为该粒子只受到以该粒子为圆心，半径h以内的所有其他粒子的影响，h称为光滑长度。

式中：t为时间；mb为质点密度；vab为va-vb即粒子速度的矢量差，a和b为粒子编号；Wab为核函数。核函数的选取决定了算法的精度及计算速度，本文选用了Wendland五次核函数［7］，其数学式为：

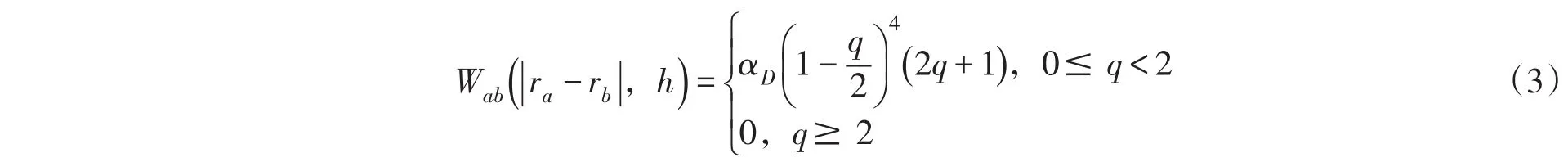
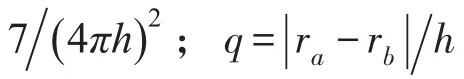
用Monaghan J J的方法［8］将式（1）中的压力项离散化。

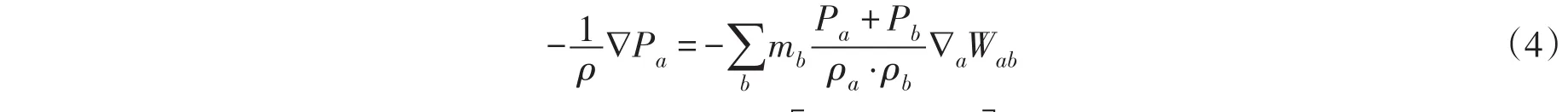
SPH方法常用人工黏性表征水体的黏性，但本文中流场雷诺数较大，考虑到紊动切应力的存在，将耗散项Γ表示为层流黏性项和紊流黏性项之和。

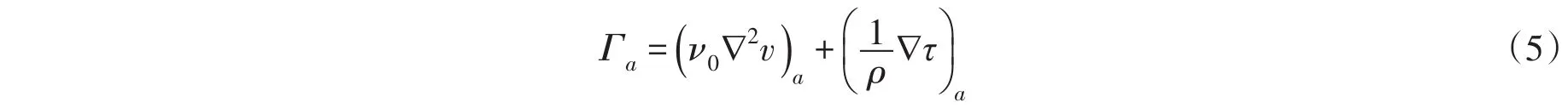
层流黏性［11］表示为

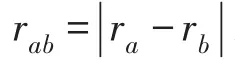
紊流黏性［12］表示为

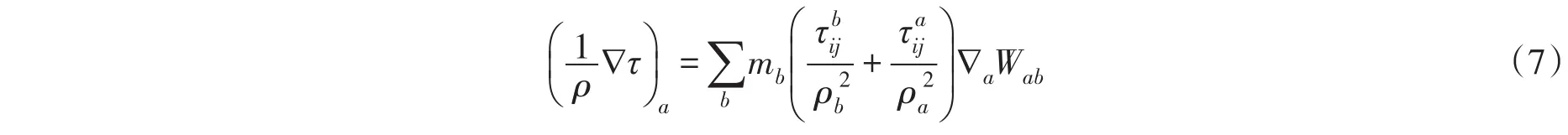
将式（4）—式（7）代入式（1）得：

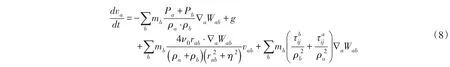
本数模的模拟时间长达120 s，故采用二阶显式Symplectic算法［13］，可在长时间模拟中保持较高的计算精度。

2.2 水动力边界条件 水槽的固壁边界采用动力学边界粒子法［14］，在固壁边界上排布2层与流体粒子相同属性的边界粒子，通过与流体粒子间的连续性方程求得其物理量。具有计算上的便捷性和对复杂边界问题的适应性。

为使计算区域中的流体质点保持稳定的循环流动，将周期性边界条件和流速边界条件相结合，模拟了物理模型实验中水泵的功能。首先将流出计算区域的粒子从计算域的另一端重新加入流场，使模拟过程中计算区域中的粒子总数不变。同时，在周期性边界边缘的粒子也会与另一侧周期性边界边缘的粒子相互作用，避免了边界粒子缺失的问题［15］。在粒子的出入口一定长度的区域内的粒子强制赋予流速，使得计算区域中的粒子受到流速边界处粒子的影响，而流速边界处粒子则不受到计算区域粒子的影响［4］，如图1所示。

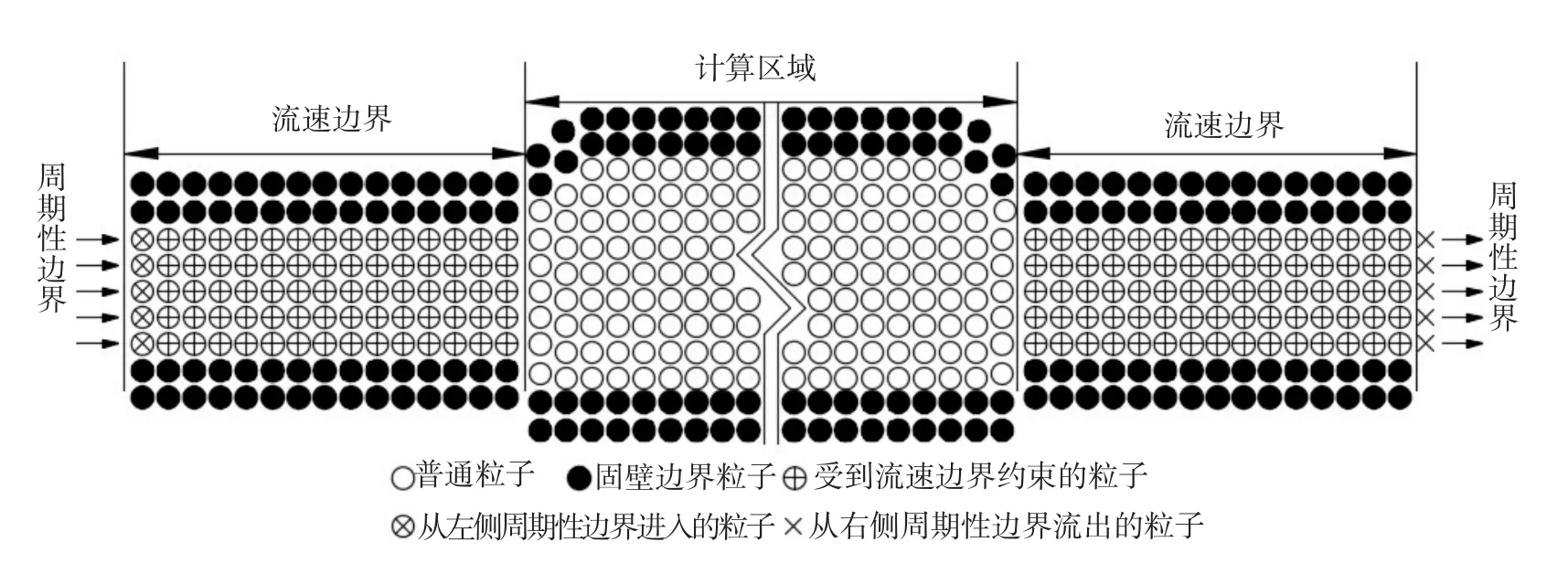
图1 边界粒子分布示意图

2.3 数值整流区域 疏密不均的整流网可将均匀流非均匀化，亦可将非均匀流均匀化。若假设流体为无旋流，则整流网的流速重分布作用主要与整流网阻流系数K和上游流速U有关。以剪切流为例，若整流网上游为流速为U的均匀流，下游产生流速分布为u的剪切流，如图2所示。流速u(y)分布规律为：

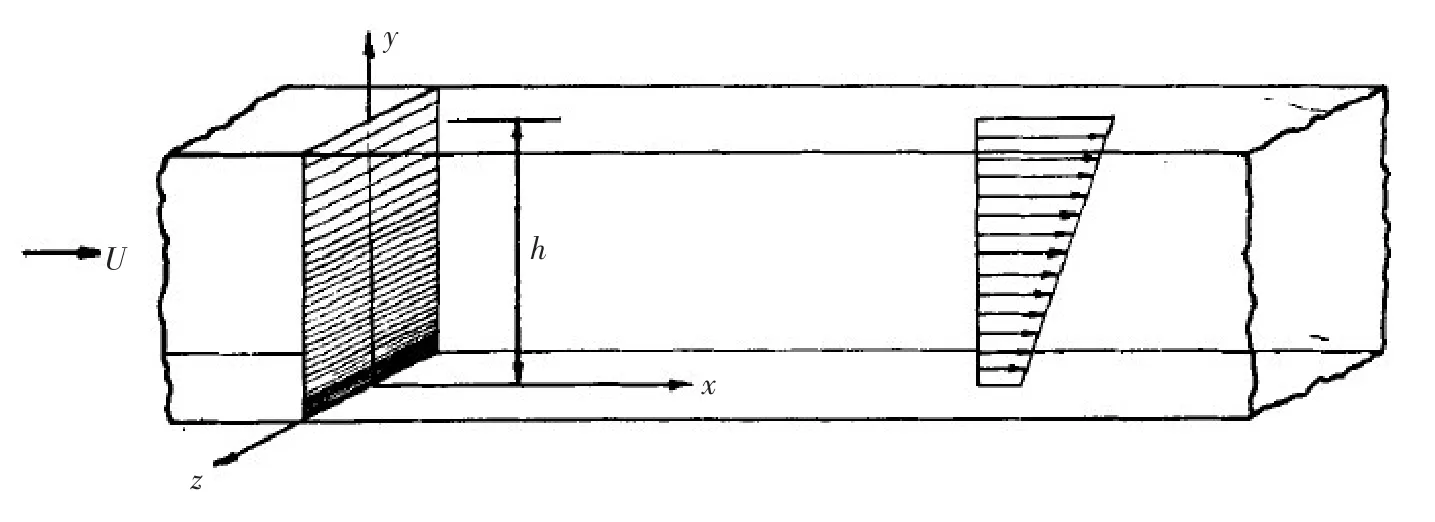
图2 网格分布与流速分布的关系［16］

系数λ满足：

整流网对流体湍流度具有调节作用。整流网既可提高流体的湍流度，亦可降低流体的湍流度。整流网下游的湍流度主要由上游流体透过整流网的湍流、整流网本身产生的湍流和下游流体不匀均流衰减过程中产生的湍流组成［3］。其中整流网产生的湍流主要与整流网的孔隙率ξ和基于丝径的雷诺数Rd有关。对于盲沟整流网，当ξ≤ 0.3且Rd＜40时，整流网本身不会产生湍流［17］。

整流装置前后的速度平方差为：

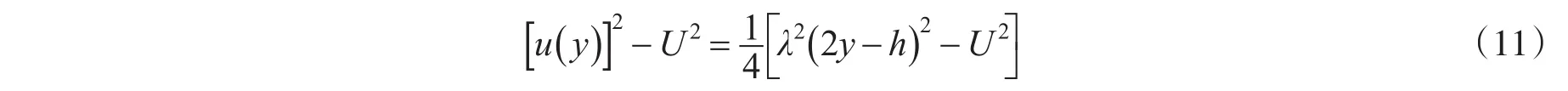
在计算域中设定阻流区域，当粒子进入该区域时，除粒子间相互作用以外，还会受到阻流区域的作用。

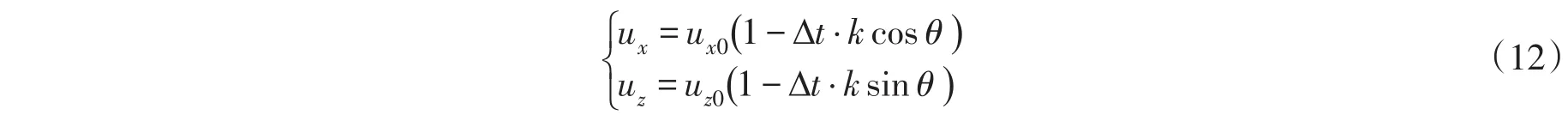
式中：系数k为阻流系数，l为整流段的厚度；α为修正系数，通过试算确定；θ为设定流向与水平方向的夹角，通过设定合适的θ，可令阻流区域只约束粒子在指定方向的速度。由于阻流区域在垂直方向阻流系数不相同，粒子经过阻流区后即会产生不同的流速梯度。通过调节合适的修正系数，即可模拟实际整流网的整流效果。

3 水槽物理模型实验

为了验证盲沟材料在造流水池中的整流效果，在天津大学“水利工程仿真与安全国家重点实验室”建设如图3所示的造流水槽物理模型。模型水槽基本尺寸与数学模型中的相同，水流由图3中左侧水泵推动之后，通过进水口进入水槽，再由出水口经右侧水泵，通过水槽下方的回水廊道回到左侧。回水廊道内设有回流水泵，用于补偿水流流经回水廊道的能量损失，使a处和f处的水位保持一致。由于水槽的两端各设有一个相同的水泵，可认为水槽两端具有相同的流速边界条件，与数学模型中的流速边界吻合。

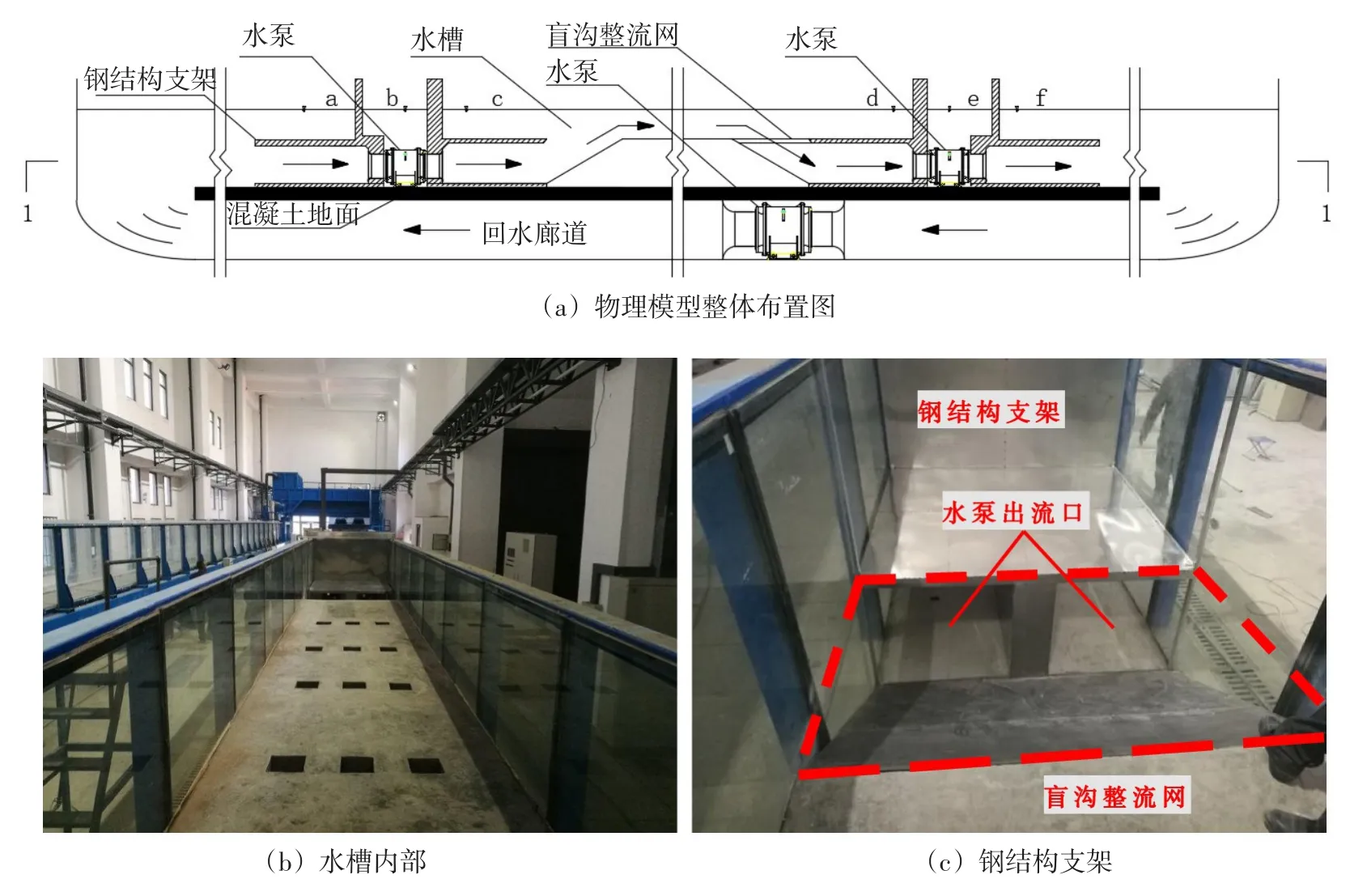
图3 造流水槽物理模型整体布置图

实验水槽中的水泵流量与水泵电机频率和水泵两侧的水位差有关。通过预实验试测得到水泵流量与水槽内水深及电机频率的对应关系如表1和图4所示。

表1 水泵流量与水深和频率对应关系 （单位：m3/s）

图4 水泵流量对应关系图

实际流入水槽的流量并不等于水泵的造流流量，而是满足式（13），如图5所示。

图5 泵室水流流态示意图（单位：Hz）

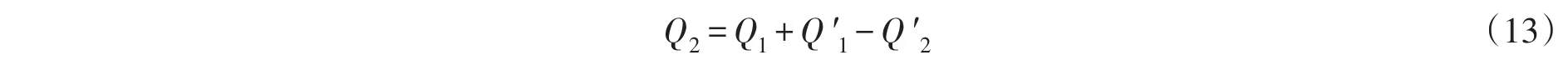
随着水泵频率增大，水泵桨叶旋转变快，廊道抽水流量Q1随之增大，出流口实际流量Q2增大。随着水槽内水深增大，水泵内部流量略有增大，这是由于水泵的安装方式属于湿式安装，水泵出流口与水槽进口之间存在缝隙。水深较小时，泵口回流流量Q′2增大，出流口实际流量Q2减小，即实际流入水槽内的流量较小。

将盲沟整流网布设在水槽的末端，如图6所示。分别将水深调整为25、35、45和55 cm，在距离进水口2.25、4.25、6.25、8.25和10.25 m处各布置一个流速传感器，测量水下距离水面10 cm处流速，如图7所示。

图6 盲沟整流网安装位置

图7 流速测点布置图（单位：mm）

4 水槽数值计算分析

4.1 数模整体布置及有效性分析 如图8所示，模型水槽总长22.19 m，中部平台底长14.62 m，水池深1.25 m。模型有效性主要与水槽入口处的流速有关。理论上，深度方向粒子布置得越多，计算结果越理想。取粒子间距的最不利工况（水深25 cm），先后将粒子间距设置为0.04、0.03、0.02、0.01和0.005 m分别试算。分别测量各个粒子间距条件下图8中阴影区域的垂向流速分布，绘制在半对数坐标系中，如图9所示。

图8 造流水槽计算模型整体布置图 （单位：m）

如图9所示，当粒子间距小于0.01 m时，流速分布不再受到粒子间距的影响，可以认为0.01是足够有效的粒子间距。考虑计算耗时，取0.01 m为模型的粒子间距。

图9 不同粒子间距入口垂向流速分布对比图

数模中的流速分布需与物模实验结果相对应。取水深的最不利工况（水深75 cm），将数模和物模中的入口流速垂向分布绘制在半对数坐标系中，结果如图10所示。由图10可知，数模中的入口流速垂向分布与物理模型实验结果吻合较好，且整体上呈对数分布，符合紊流的流速分布特征。可以认为本数模中的流速分布真实有效。

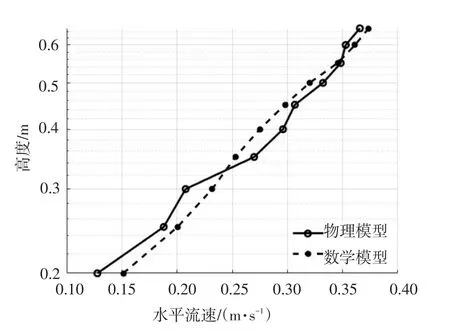
图10 出流口处垂向流速分布对比图

4.2 实验水槽流速分布对比 测量有整流装置时的水槽内部沿程流速分布情况，分别与有无整流装置的数模结果比对，如图11所示。

图11中，当水深小于35 cm时，无论是否加入数值整流区，数模中物模的流速数据均拟合较好；当水深大于45 cm时，数值整流区对流速分布影响显著。无整流区时，55 cm水深的数模物模差异达到40.36%，有整流区时，数模物模差异在小于10%。这是因为高水深条件下，流速测量点刚好位于流体上侧的低流速区域。如图12和图13所示，图中不同灰度表示不同流速分布，流速随颜色深度加大。“×”表示距离进水口10250处的测点位置。无整流区的组次中，由于测点位于上侧的低流速区流速偏小，表现为图11（d）中10 250处的最小值；有整流区的组次中，由于低流速区长度得到有效控制，测量流速与物模结果吻合。水深55 cm，频率25 Hz条件下各水平位置流速分布如图14所示。

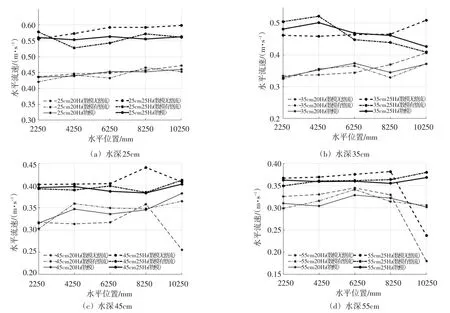
图11 不同水深条件下不同水平位置流速对比图

图13 55cm水深条件下有数值整流区域时水槽末端流速分布着色图

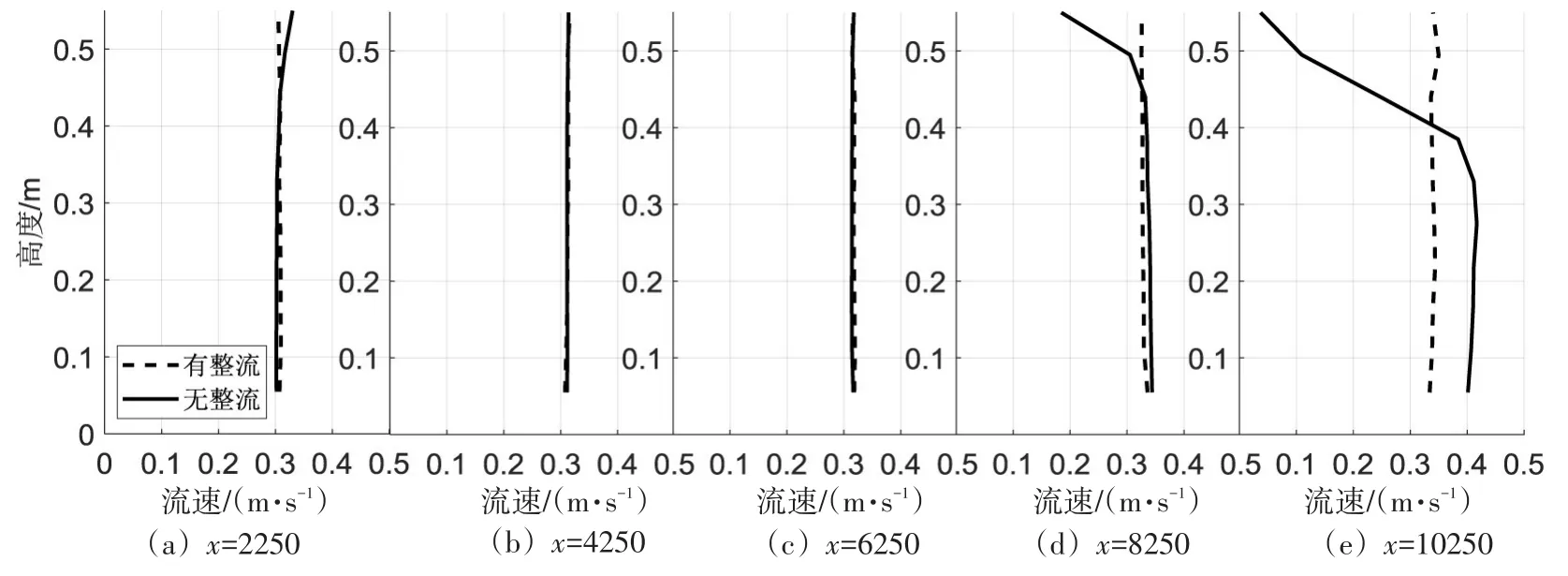
图14 55cm水深条件下不同水平位置流速分布图

5 结论

（1）将流速边界条件和周期性边界条件相结合，形成了稳定的流场。通过与物模实验中进水口的流速分布相对比，说明了数学模型的合理性。结果表明，当粒子间距足够小时，可以得到稳定、合理的流速场。

（2）整流网相关理论可应用在SPH方法当中，模拟实际整流网对剪切流的整流效果。本文根据未加整流区域时的流速分布规律设置了数值整流区域，并验证了整流效果。物模实验显示，有整流网的工况中水槽中部流速分布均匀。数模实验显示，未加数值整流区域时，流速分布与物模结果相差较大；加入整流区域后，流速分布与物模结果对应较好。

（3）整流网的整流效果与水深有关。当水深小于35 cm时，不同水深的流速差异较小，数值整流区域对流速的影响并不明显。当水深大于45 cm时，未添加数值整流区域的数值模拟结果与物理模型实验差异较大，添加数值整流区域的数值模拟结果与物理模型实验结果相符。因此，本文的数值整流方法可显著改善大水深条件下的垂向流速均匀性。

需指出的是，受实验条件限制，本文未能测量出物模实验中无盲沟整流材料时水槽尾端的流速分布，而是通过有效性验证的数模结果作为替代。且本文未能测量出物模实验中水槽末端的流速的局部分布，而是通过水槽内部的流态间接反映水槽尾部的流态。该缺陷可能导致数值阻尼区域的阻流系数取值存在偏差。该偏差可通过调整修正系数α作为弥补。