级间热分离条件下双级延伸喷管展开过程动力学耦合仿真研究①
2021-05-17赵博文宋学宇曹涛峰
任 萍,赵博文,陈 鹏,宋学宇,2,曹涛峰
(1.中国航天科技集团有限公司四院四十一所,西安 710025;2.西北工业大学 航天学院,西安 710072)
0 引言
为改善飞行级的质量特性以获得更好的加速和运载性能,需要在飞行过程中进行热分离从而将无用的质量抛掉以减少导弹的冗余质量[1],因此战略导弹为增加射程一般采用多级动力系统。延伸喷管一般多用于多级导弹的第二级或第三级固体火箭发动机上,延伸喷管的展开过程与导弹的级间热分离过程在一定程度将产生重合,其展开过程受到级间瞬态流场、展开动力学、展开能源系统以及级间相对运动等多个物理过程的耦合影响,展开条件十分复杂。为保证延伸喷管在级间热分离时的正常可靠展开,必须研究级间热分离对延伸喷管展开过程的影响,从而对延伸喷管结构、展开能源、展开时间和级间段结构及级间分离时序等进行合理的设计和选择。
带有延伸喷管的固体火箭发动机进行级间热分离时,其基本过程主要有以下几个步骤:上面级发动机点火,级间连接件爆炸螺栓炸断并解锁分离,延伸喷管展开,安全分离等[2]。为了避免延伸喷管在展开时与下面级发动机前封头发生碰撞等情况,一般将级间分离时刻和延伸喷管展开时刻之间设置一短暂的时差。目前针对延伸喷管展开过程的研究,王成轩等[3]和尤军峰等[4]根据理论力学中质心运动定理或达朗贝尔原理对延伸喷管展开动力学进行了分析建模和数值计算;王博哲等[5]和白宏伟等[6]对延伸喷管在地面展开时喷管尾流场进行了瞬态仿真计算;刘华坪等[2,7]对带有双级延伸喷管的固体火箭发动机热分离过程级间段流场进行了数值计算。
以往的研究并未对延伸喷管展开过程和级间热分离过程之间的耦合影响进行深入研究,而延伸喷管能否在复杂条件下正常可靠地展开关乎发动机的飞行成败,因此本文对级间热分离条件下双级延伸喷管展开过程进行动力学耦合仿真计算,重点研究延伸喷管能源系统输入参数大小、级间分离时刻和延伸锥开始展开时刻等因素对其展开过程的影响情况。
1 计算模型和计算方法
1.1 动力学计算模型
文献[8]中,作者以图1所示的作动筒式双级延伸喷管及其展开能源系统为研究对象,假设作动筒中筒相对内筒的位移为f(t),对其展开动力学与能源系统进行了分析建模,即得到式(1)所示的一个双级延伸喷管展开动力学与能源系统供气过程耦合的一阶微分方程组初值问题。
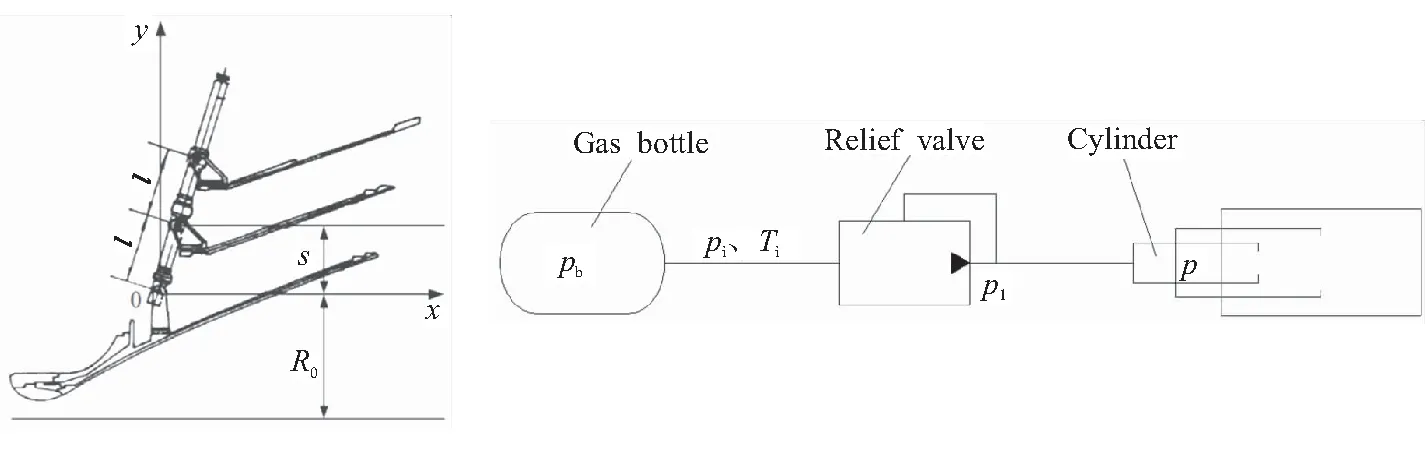
(a)Double extendible nozzle (b)Gas supply energy system
(1)
式中Z1(t)=l+f(t);Z2(t)=Z1′(t);Ff01为内作动筒与中间作动筒的摩擦力;Fgpx为两级延伸锥在流场中受到的总轴向气动力;f(t)、f′(t)、f″(t)分别为t时刻中间作动筒相对于内作动筒的位移、速度、加速度;l0、l1、l2分别为内作动筒、中间作动筒、外作动筒各自质心与其支耳中心的距离;s为中间作动筒支耳距离固定支耳的竖直高度差;M0、M1、M2、M3、M4分别为内筒、中筒、外筒以及Ⅰ、Ⅱ级延伸锥各自的质量;pb为气瓶压强;q为减压阀流量;p为作动筒内压;k为气体比热比;R为气瓶工质气体常数;Tb0、pb0分别为初始状态时气瓶内气体的温度和压强;Cv为阀门流量系数;A为阀门流通面积;pi、Ti分别为气瓶出口处气体压强和温度;p1、T1分别为阀门出口处气体压强和温度;V0为初始时刻管路与双级作动筒等效体积之和;Ain为内作动筒横截面积;Amid为中筒横截面积;Aout为外筒横截面积。
通过Runge-Kutta法数值求解式(1)中的常微分方程组即可得到延伸锥的展开特性如轴向位移、速度及加速度以及气瓶和作动筒内压的变化情况。
1.2 动力学方程组求解参数设置
耦合仿真计算中需要数值求解式(1)所示的动力学(微分)方程组,因此需要给定动力学方程中相关参数的初始条件,其主要包括双级延伸喷管展开机构初始几何参数,气动能源系统中气瓶、减压阀和输气管路的初始几何参数和气动参数(展开能源为氮气)等,各参数具体数值如下所示。双级延伸喷管展开机构参数:l=0.13 m,l0=0.168 m,l1=0.131 m,l2=0.08 m,s=0.1236 m,M0=2.5 kg,M1=0.6 kg,M2=0.6 kg,M3=50 kg,M4=50 kg。气瓶、减压阀和输气管路及气源参数:Vb0=0.002 m3,Tb0=253 K,Cv=0.06,A=0.0007 m2,V0=0.00049 m3,Ain=0.00196 m2,Amid=0.00238 m2,Aout=0.00282 m2。
1.3 流场计算模型
1.3.1 几何模型
带有双级延伸喷管的发动机级间段结构如图2所示。为简化计算本研究采用二维轴对称模型进行流场仿真计算,将导弹壳体上沿周向均布的多个方形排气窗口按照面积大小等效为环状孔[9]。当导弹未进行级间解锁分离时,将发动机级间分离面(图2中Stage separation surface)设为固体壁面,当级间段解锁分离后,将其重设为内部连通边界。
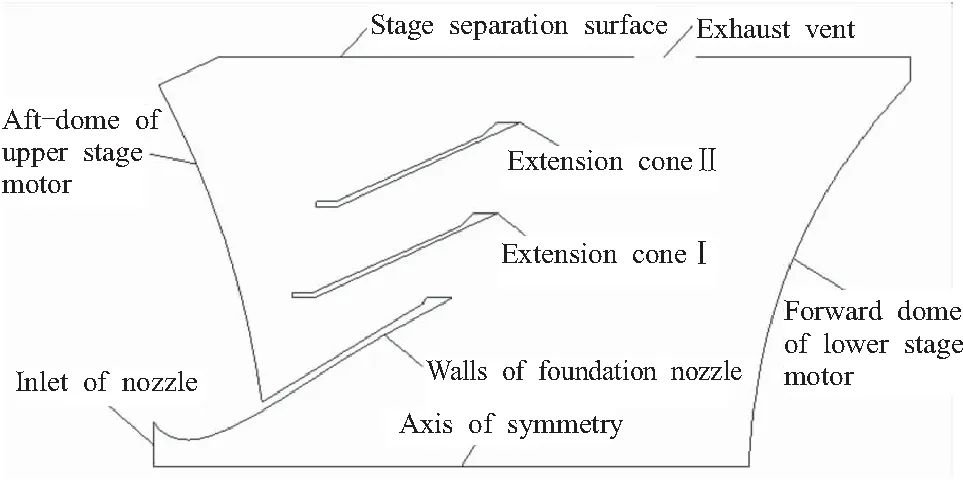
图2 发动机级间段结构简图
由于级间段解锁后的热分离过程时间较短,上面级发动机在该过程中速度变化较小,热分离时两级发动机间的距离变化主要由下面级发动机的运动特性决定,因此在仿真计算中假定上面级发动机速度不变(相对来流速度为零),下面级发动机在气动力和自身后效推力的作用下沿喷流方向运动。考虑到在短时分离过程中下面级发动机的质量和结构变化不大,为简化计算将下面级发动机视作等质量刚体处理,且不考虑其姿态的变化[10],根据牛顿第二定律F=m·(dv/dt)可用式(2)、式(3)描述其速度、位移运动规律:
(2)
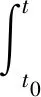
(3)
式中F(t)为t时刻下面级发动机受到的气动力和后效推力沿轴向的合力,级间热分离过程认为下面级发动机后效推力为100 kN并保持不变;mxia为下面级发动机质量,mxia=4500 kg;v(t0)、v(t)为t0和t时刻下面级发动机的速度;s(t0),s(t)为t0和t时刻下面级发动机的位移。
1.3.2 网格模型
图3展示了级间热分离初始时刻流场网格模型图,计算中将发动机内外流场进行一体化计算,对双级延伸喷管的基础喷管壁面、Ⅰ级和Ⅱ级延伸锥壁面,级间区以及下面级发动机前封头等进行网格加密。

(a)The whole flow field grid

(b)Interstage flow field grid
动网格采用基于弹簧光顺、动态层以及网格重构的网格更新方法,为满足动网格计算需要,采用分区网格划分策略,对远场和喷管内流场采用结构化网格,对级间区采用非结构网格[11]。图4为级间热分离时延伸锥处于不同位置时的网格分布图。

(a)Extension cone at initial position (b)Extension cone at middle position (c)Extension cone at final position
1.3.3 求解条件与边界条件
在耦合仿真流场计算部分,在Fluent中采用密度基隐式求解器求解,对流项采用2阶迎风格式及AUSM通量格式,瞬态项采用1阶隐式离散格式,湍流模型为RNGk-ε模型并采用非平衡壁面函数。
模拟飞行高度为25 km时的级间热分离过程,来流马赫数为3,流场边界条件如下:
(1)压力入口:总温为3751 K,总压按照图5所示升压曲线变化。
(2)压力出口:出口压强为2549.22 Pa,温度为221.5 K。
(3)压力远场:来流(静)压强和温度与压力出口一致,来流马赫数Ma=3。
(4)固体壁面:非滑移绝热壁面。
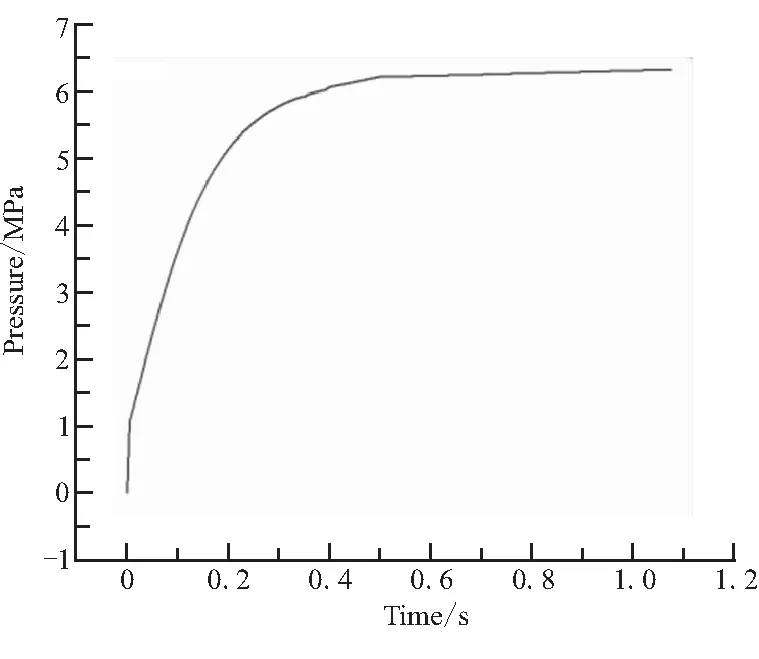
图5 基础喷管入口压强变化曲线
1.4 耦合仿真方法
本文按照图6所示流程进行耦合仿真求解,求解思路大致为:利用Fluent软件UDF功能,将描述延伸喷管展开动力学模型、能源系统模型以及下面级发动机刚体运动模型的(微分)方程组通过C语言编译到软件中,通过Fluent流场模块求解气动参数,将延伸锥和下面级发动机受到的气动力大小传递给UDF中的动力学微分方程组。UDF通过数值求解动力学微分方程组得到延伸锥和下面级发动机的位移、速度和加速度,并将速度值返回给Fluent流场模块作为动网格划分的依据。Fluent通过动网格方法在每一时间步上更新网格,并判断延伸锥是否运动到指定位置处,若延伸锥到达预定位置,则停止计算;若延伸锥未达到预定位置,则再次计算延伸锥和下面级发动机上的气动力大小并返回给UDF函数,如此往复迭代,从而实现对级间热分离条件下延伸喷管展开过程的耦合求解。
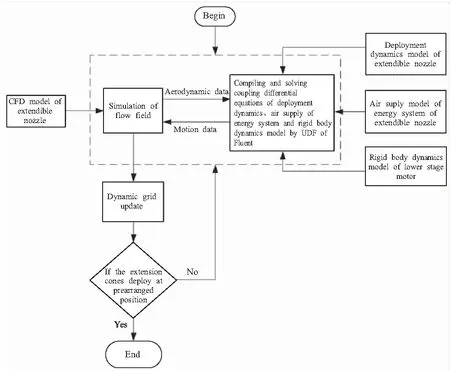
图6 级间热分离耦合仿真流程图
2 仿真计算结果
在流场仿真计算中,将0~tf时间段模拟为发动机点火建压阶段,该时段内延伸锥呈收拢状态,两级发动机保持相对静止;接着,级间连接件在tf时刻断开,下面级发动机与上面级发动机开始分离;随后,延伸喷管展开机构在ts时刻接到展开指令进行展开运动。瞬态时间步长设置为0.000 1 s,总计算步数根据延伸锥展开到位时间决定。以气瓶初始压强pb0=1.4 MPa,分离时刻tf=0.13 s,开始展开时刻ts=0.2 s的计算结果为例分析流场变化。
在双级延伸喷管展开动力学、展开能源系统和下面级发动机刚体动力学计算部分,通过瞬态耦合仿真计算,对比研究了在给定不同的气瓶初始压强pb0、不同分离时刻tf以及不同展开时刻ts的条件下延伸锥在流场中的运动和壁面气动力的变化情况。
2.1 流场计算结果
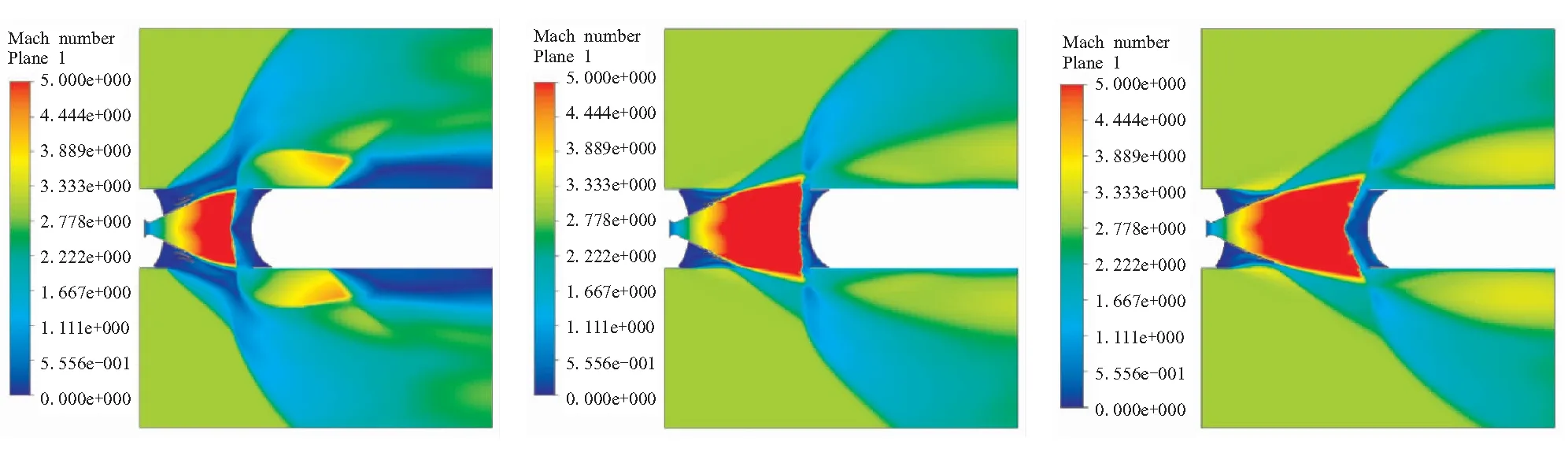
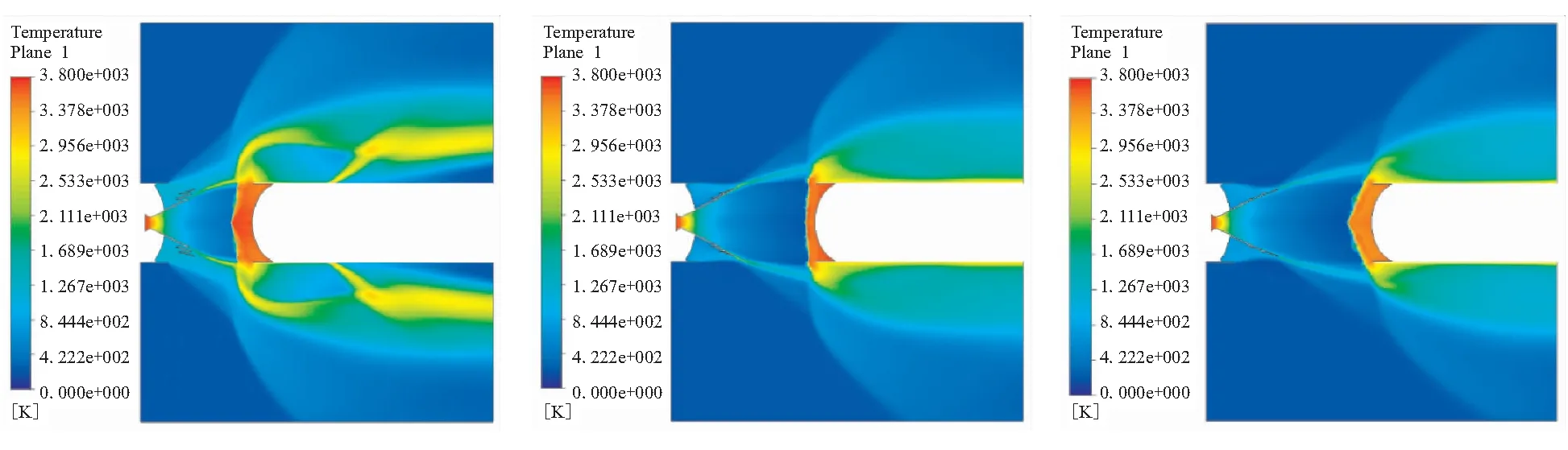
模拟导弹高空飞行时进行一二级热分离过程,通过瞬态耦合仿真计算得到如图7~图10所示的在给定的条件下流场计算域的压强、马赫数、温度及速度矢量随时间变化云图。分析流场变化情况可得到以下结论:
(1)由图7和图8可看出,在级间热分离过程中,由于下面级发动机前封头对喷管出口燃气的阻碍,在基础喷管出口附近形成了正激波,从而在下面级发动机前封头附近形成一高温高压区域,同时在级间段空腔内和下面级发动机前封头以及排气口外壁面附近产生较强的漩涡流动。随着级间连接件的断开和两级发动机开始分离,激波从基础喷管出口附近的位置开始逐渐远离,激波后以及级间区的压强逐渐降低。在排气口附近,由于级间区燃气从排气口高速排出,远场超声速来流受到出口燃气的阻碍而产生明显的激波结构,随着级间分离距离的增大,排气口附近的激波强度逐渐减弱。
(2)由图9和图10可看出,在级间分离初始阶段由于下面级发动机前封头的阻碍及排气口较小的原因,喷管出口燃气经过壁面反射后一部分从排气口流出,另一部分通过延伸锥与壁面间的狭缝迴流至级间区,使得级间段区域温度急剧上升,在0.13 s开始进行级间分离时级间段空腔内和延伸锥附近的温度接近3800 K,此时发动机后封头、基础喷管外壁面和Ⅰ、Ⅱ级延伸锥及其展开机构附近热环境非常恶劣。随着分离面的抛离和级间分离距离的增加,此时燃气主要从排气口排出,燃气迴流逐渐消失,级间区温度逐渐降低,0.2 s时刻级间段空腔内温度已降至900 K左右,延伸锥展开到位后该空腔内温度稳定在780 K附近。
(3)在级间分离和延伸锥展开过程中,级间段流场存在复杂的激波结构并伴随其位置移动过程,同时还产生强烈的漩涡流动和湍流脉动[12],导致延伸喷管展开时其壁面气动力波动剧烈,既要保证延伸锥的及时展开,同时还要求延伸锥展开过程平稳且可靠,因此需要合理地进行分离和展开时序的选择与匹配。
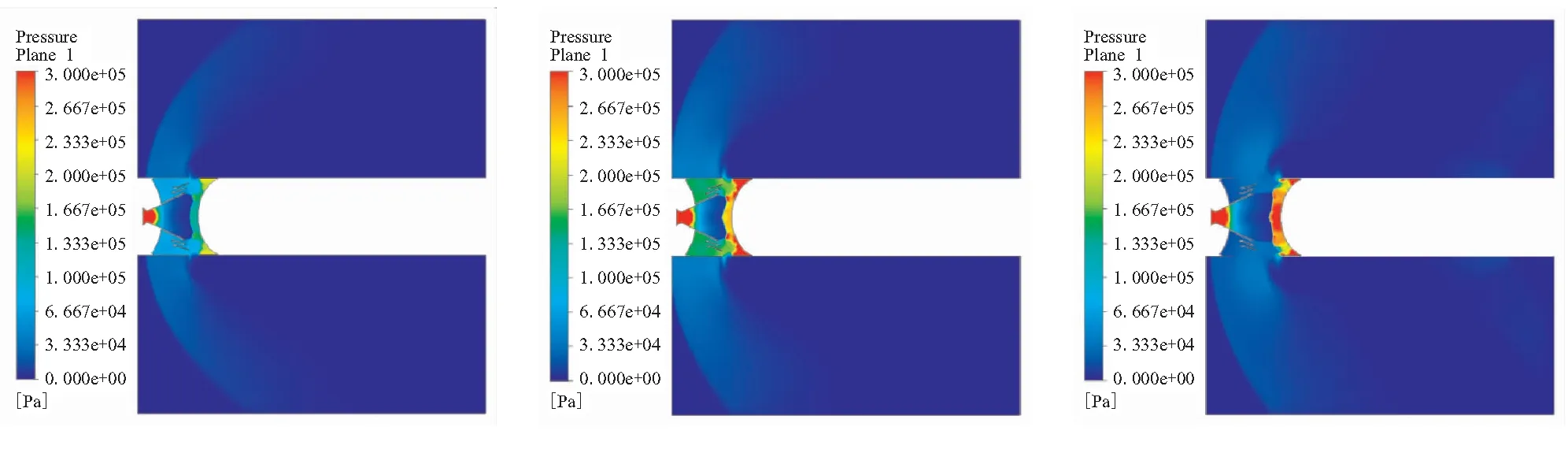
(a)t=0.05 s (b)t=0.13 s (c)t=0.2 s
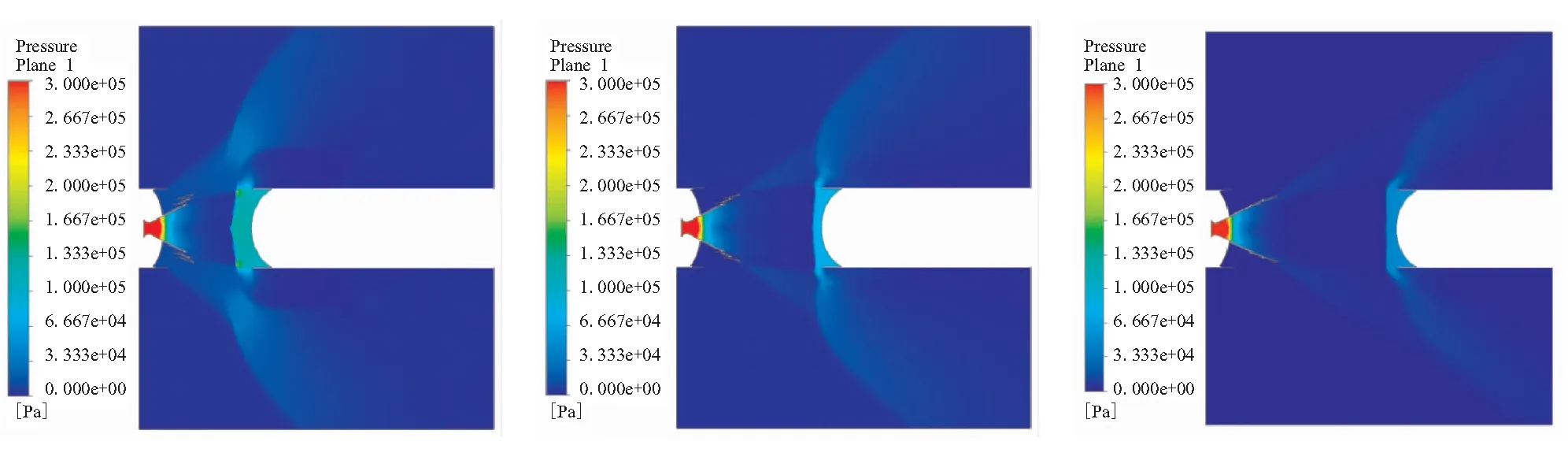
(d)t=0.27 s (e)t=0.33 s (f)t=0.39 s
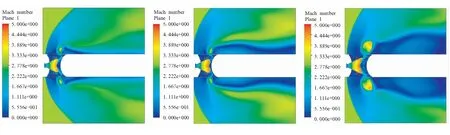
(a)t=0.05 s (b)t=0.13 s (c)t=0.2 s
(d)t=0.27 s (e)t=0.33 s (f)t=0.39 s
(a)t=0.05 s (b)t=0.13 s (c)t=0.2 s
(d)t=0.27 s (e)t=0.33 s (f)t=0.39 s

(a)t=0.05 s (b)t=0.13 s (c)t=0.2 s
(d)t=0.27 s (e)t=0.33 s (f)t=0.39 s
2.2 动力学计算结果
2.2.1 气瓶初始压强对延伸喷管展开过程的影响研究
以往研究表明,级间热分离时,当展开力较小时延伸喷管可能无法展开,因此气瓶初始压强的取值大小至关重要。保持级间分离时刻为0.13 s和延伸锥开始展开时刻为0.2 s不变,本节研究了气瓶初始压强取不同值时延伸喷管的展开特性和受力情况。
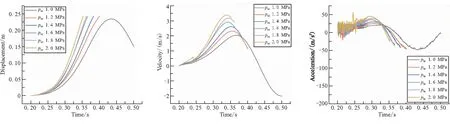
表1给出了在不同气瓶初始压强pb0作用下延伸锥展开到位所用的时间t。由表1可知,当气瓶初始压强等于(或小于)1.0 MPa时延伸喷管无法展开到位,当气瓶初始压强大于1.2 MPa时,气瓶初始压强越大延伸喷管展开越快。

表1 不同气瓶初始压强下延伸锥展开时间
图11对比了在不同气瓶初始压强作用下Ⅰ级延伸锥展开运动特性。
(a)Axial displacement (b)Axial velocity (c)Axial acceleration
由图11可知,级间热分离时,当气瓶初始压强等于(或小于)1.0 MPa时,延伸喷管无法展开到位并出现收拢运动。气瓶初始压强越大,延伸锥展开到位时的速度和加速度越大,延伸锥对接时的冲击力也更大,不利于对接时的结构安全。
图12对比了在不同气瓶初始压强作用下Ⅰ、Ⅱ延伸锥受到的总轴向气动力随时间变化曲线。
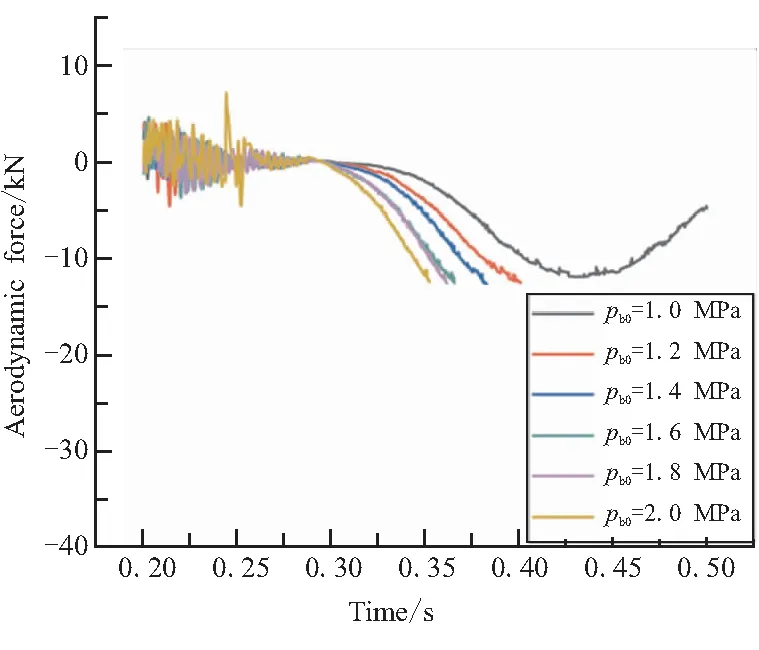
图12 不同初始压强下Ⅰ、Ⅱ级延伸锥 总轴向气动力变化曲线
由图12可看出,延伸喷管展开前期,延伸锥壁面气动力波动剧烈,随着延伸喷管的展开,该气动力波动趋于平缓,其值变为负值且越来越大,表明气动力对延伸喷管的展开阻碍作用越来越大,当延伸喷管展开到位后,该气动力均达到最大值为-12.3 kN左右。综合考虑延伸锥的展开可靠性及结构安全,在保证延伸喷管展开时间和安全裕度达到要求的条件下,气瓶初始压强可取1.4 MPa。
2.2.2 分离时刻对延伸喷管展开过程的影响研究
级间分离时刻的选取影响着分离前级间段的“憋压”程度和延伸喷管的展开特性。保持气瓶初始压强为1.4 MPa和延伸锥开始展开时刻为0.2 s不变,参考某型号级间分离时刻并在附近取值,通过仿真计算得到当分离时刻取不同值时延伸喷管的展开特性和受力情况。
表2给出了在不同分离时刻tf下延伸锥展开到预定位置所用的时间t,图13对比了不同分离时刻下延伸锥的展开运动特性,图14对比了不同分离时刻下Ⅰ、Ⅱ级延伸锥总轴向气动力随时间变化曲线。由表2可知当延伸喷管开始展开时刻不变时,级间分离时刻越早,延伸喷管展开越慢。其原因由图14可知,在延伸喷管展开初期,虽然延伸锥壁面气动力的波动较大,但波动区间主要在正值部分,表明级间段内气动力对延伸喷管的展开起到促进作用。若级间分离时刻越早,当延伸喷管开始运动时,两级发动机之间分离距离越远,燃气迴流减弱,流场气动力对延伸喷管展开的促进作用减弱,因此延伸喷管展开较慢。

(a)Axial displacement (b)Axial velocity (c)Axial acceleration

表2 不同分离时刻下延伸锥展开时间
根据总体控制需求,一般要求延伸喷管在点火后0.5 s内展开到位,给定的四种工况下延伸喷管展开用时皆满足要求,但由图13、图14可见,级间分离越晚,延伸锥壁面气动力及其展开加速度波动更大,延伸锥展开到位时的速度也更高,为提高延伸喷管展开过程和对接时的结构安全,级间分离时刻应适当提前。
2.2.3 开始展开时刻对延伸喷管展开过程的影响研究
在级间分离时刻不变的条件下,延伸喷管开始展开时刻的选取对延伸喷管展开特性同样有所影响。保持气瓶初始压强为1.4 MPa和级间分离时刻为0.13 s不变,通过仿真计算得到当延伸喷管开始展开时刻取不同值时延伸喷管的展开特性和受力情况。

图14 不同分离时刻下Ⅰ、Ⅱ级延伸锥总轴向 气动力随时间变化曲线
表3给出了在不同开始展开时刻ts下延伸锥展开到预定位置所用的时间t,由表3可看出在级间分离时刻不变时,延伸喷管展开时刻越晚,延伸锥展开到位用时越长,其原因与第2.2.2节中基本一致,即双级延伸喷管开始展开时刻越晚,当延伸喷管开始展开时两级发动机之间的分离距离越远,此时级间段流场气动力对延伸喷管展开前期的促进作用减弱,因此延伸喷管的展开过程用时更长。

表3 不同开始展开时刻下延伸锥展开时间
图15对比了不同开始展开时刻下延伸锥的展开运动特性,图16对比了不同开始展开时刻下Ⅰ、Ⅱ级延伸锥总轴向气动力随时间变化曲线。由图15、图16可看出当延伸喷管开始展开时刻越晚,延伸喷管展开用时更长,但延伸锥展开加速度和壁面气动力波动幅度更小,延伸锥展开到位时的速度也更小,延伸锥对接时的冲击将更小,因此有利于提高延伸喷管展开过程的平稳性和对接时的安全性。
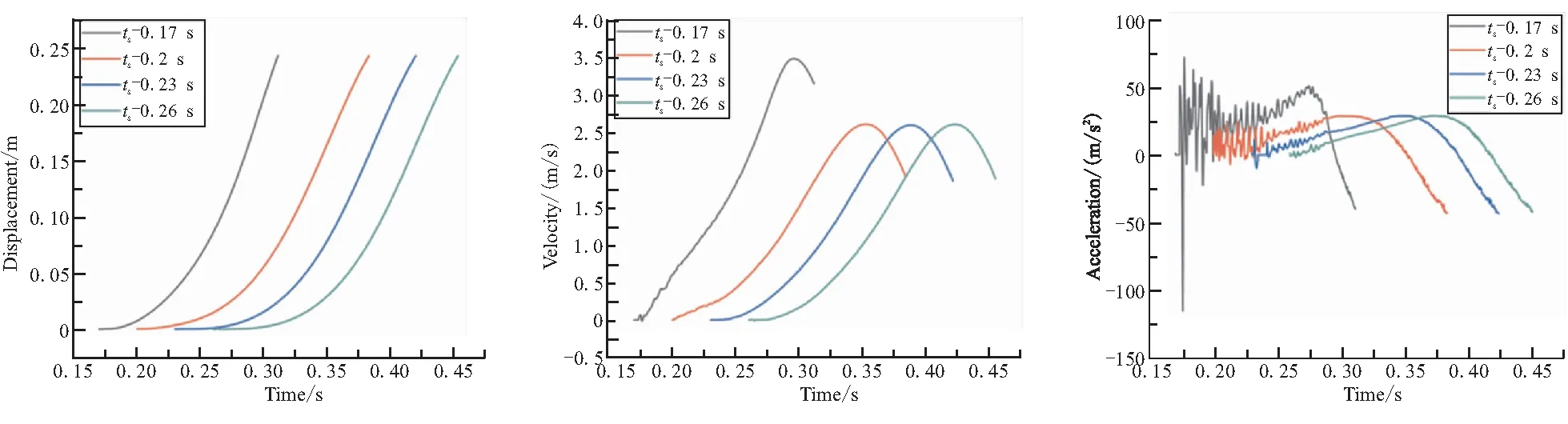
(a)Axial displacement (b)Axial velocity (c)Axial acceleration

图16 不同开始展开时刻下Ⅰ、Ⅱ级延伸锥 总轴向气动力随时间变化曲线
3 结论
本文通过对级间热分离条件下双级延伸喷管展开过程动力学耦合仿真分析,可以得到如下结论:
(1)在级间热分离时,由于燃气的迴流,级间段与延伸锥壁面要承受短时高温影响,瞬时温度最高接近3800 K,因此必须对基础喷管、延伸锥及其展开机构采取相应的热防护措施,级间段流场波系结构复杂且存在激波运动,使得延伸锥展开时其壁面气动力载荷波动剧烈。
(2)气瓶初始压强小于(等于)1.0 MPa时,延伸喷管无法展开到位。当气瓶初始压强大于(等于)1.2 MPa时,气瓶初始压强越高,延伸喷管展开越快,但延伸锥的展开加速度及其壁面气动力波动更大,不利于展开和对接过程的结构安全,因此气瓶初始压强取1.4 MPa可兼顾延伸喷管展开过程的可靠性和安全性。
(3)提早级间分离时刻并适当增加分离和展开时刻的间隔有利于提高延伸喷管展开过程的结构安全,但展开时间相对会更长。分离时刻和展开时刻分别取0.13 s和0.26 s的匹配关系可较好满足延伸喷管展开过程用时和展开稳定性的要求。
