基于格子Boltzmann方法的船舶风力助推转子绕流特性

穆 鑫，王 蛟，苏石川，耿珊珊，Verendiaikin German，李 毅

(江苏科技大学 能源与动力学院，江苏 镇江 212000)

0 引 言

风帆曾是船舶最主要的推进方式，随着全球能源短缺、环境污染等问题的日益凸显，船舶航运利用风能进行辅助推进再次获得广泛关注。船用风力助推转子，利用马格努斯效应，根据风速和风向的变化调整转子的速度和旋转方式，形成沿行驶方向的推力以达到降低推力成本目的[1]。其作为国际海事组织指定的节能技术，具有节能效果好，适用船型广的特点，成为相关行业的研究热点。国外已经有数艘实船应用的案例，国内尚处于理论研究阶段[2]。

船用风力助推转子通常是多个转子组合使用，对船用风力助推转子的研究简化为流体力学经典问题—— 圆柱绕流。目前，对单个或多个圆柱绕流的流动特性已进行大量研究。双圆柱作为多圆柱的基础形式，其研究结果对多圆柱绕流有重要的理论意义。近年来，何颖等[3]对在亚临界区均匀来流作用下的旋转单圆柱绕流进行了数值模拟，结果证明圆柱旋转可以大幅提高其升阻比。周凯等[4]对二维静止串联双圆柱进行了数值模拟，重点研究圆柱间距对其升阻力及尾流特征的影响。巴悦等[5]基于Fluent对串联旋转双圆柱的气动性能进行了模拟，给出了较优的排列旋转方式。聂德明等[6]对静止并列双圆柱绕流进行了数值模拟，给出了圆柱间距对尾流及其升力、阻力的影响。Yoon等[7]对不同间距下的旋转并列双圆柱流动特性进行了模拟，探究了圆柱间距以及转速比对绕流的影响，并且给出了不同间距下的临界转速。

格子Boltzmann方法（LBM）是20世纪80年代中期出现的一种新流体计算方法，具备流体相互作用描述简单、易于编程、天然并行性等优点。由于采用均匀规则的网格，LBM多被用于方形钝体绕流的研究，对圆柱等复杂曲面的研究依然欠缺。近年来，随着LBM理论的发展，能够处理复杂曲面使得LBM得以快速被推广。采用格子Boltzmann方法对并列旋转双圆柱进行模拟，对平直边界采用经典的反弹格式，而对于曲线边界采用的是具有2阶精度的反弹插值格式。研究双圆柱在不同间距比、不同转速比、不同转向下流体的相互干涉效应，以及这种干涉对双圆柱升力、阻力系数的影响，为风力转子助推的控制与设计提供相关参考。

1 数值方法

1.1 多松弛模型

为提高LBM的模拟稳定性，采用多松弛格子Boltzmann模型，速度离散模型采用文献[8]提出的D2Q9模型。分布函数f通过线性变换到矩空间m，从而建立速度空间与矩空间的联系。每一个速度矩代表一个实际的物理量，不同的物理量采用不用的松弛参数。MRT-LBM的演化方程为：

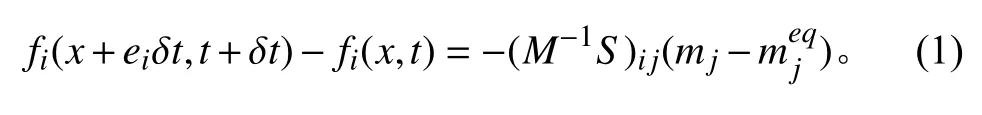
式中：f为分布函数；e为离散速度；M为变换矩阵；具体形式参见文献[9]。S为松弛参数对角矩阵；下标i，j表示离散方向（下同）；m为分布函数对应的速度矩；meq为平衡矩。

速度矩m与分布函数f之间的转换如下：

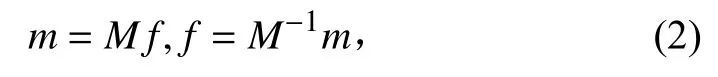
对应的平衡矩为：

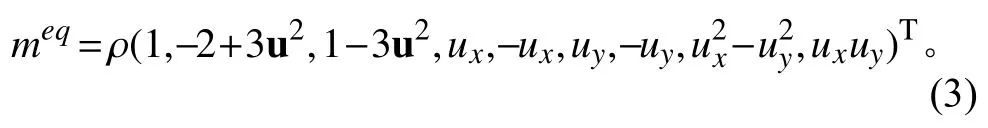
式中：ρ为密度；ux和uy分别为速度u在x和y坐标方向上的分量。

松弛矩阵为：

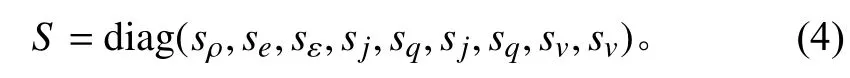
根据粒子碰撞过程的守恒定律有sρ（ρ-ρ） = 0，sj（jx-jx） = 0 和sj（jy-jy） = 0，因此sρ和sj可以选取任意值，选取sρ=sj= 0，se= 1.2，sε= 1.1，sq= 1.1，sν由流体粘度系数所决定。

1.2 复杂曲线处理

如图1所示的任意曲线边界，实心圆点xw代表的是固体边界与格子连线的交点，空心圆点xf代表流体节点，空心方形xb代表固体内的边界节点（固体内临近边界的节点），空心菱形xs代表固体节点。定义q为：

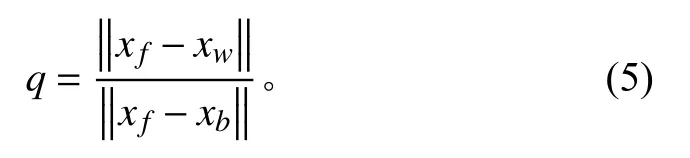
可知 0 ≤q≤1，其中xf，xb，xw分别表示网格节点f，w，b的坐标。定义由流体节点流向边界节点的粒子速度方向为ei，则反方向为e¯i。为了确定xf点处的分布函数，必出先对xb点进行插值处理。采用在碰撞之后，迁移之前对xb点进行线性插值[10]：

其中：

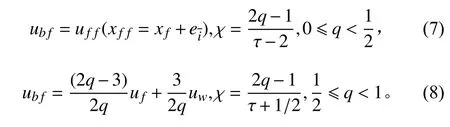
式中：wi为权重因子；f‘为碰撞后的分布函数；ubf为虚拟速度；uf为粒子位于xf点处的速度；uw为运动固体边界xw处速度；χ为由q确定的加权。定义转速比|α| =ΩD/（2U），其中Ω表示圆柱的角速度，U为来流速度。

采用动量转换法计算圆柱受到的作用力。其具体形式为：

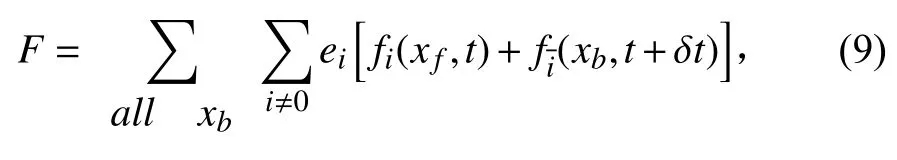
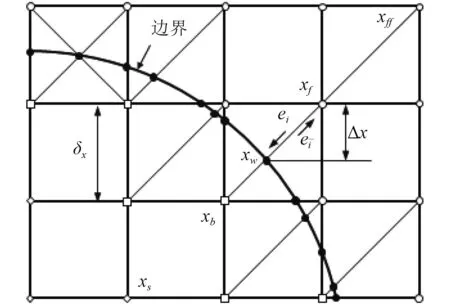
图1 空间格子和曲线壁面的分布Fig.1 Distribution of spatial lattices and curved wall

圆柱的阻力系数CD以及升力系数CL表达式如下:

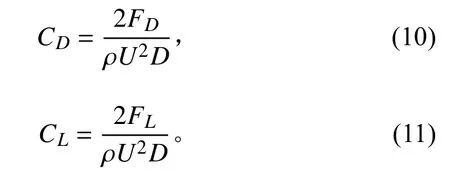
式中：FD和FL分别为圆柱所受流体作用力F在顺流方向和法线方向上的分量。

1.3 数值验证

为了验证程序的正确性以及计算结果的精度，首先模拟了静止及旋转状态下的单圆柱绕流。定义Strouhal数St=Dfv/U，其中fv为涡脱落频率。表1给出了在Re=100的情况下计算结果，并与参考文献中的数据进行对比。

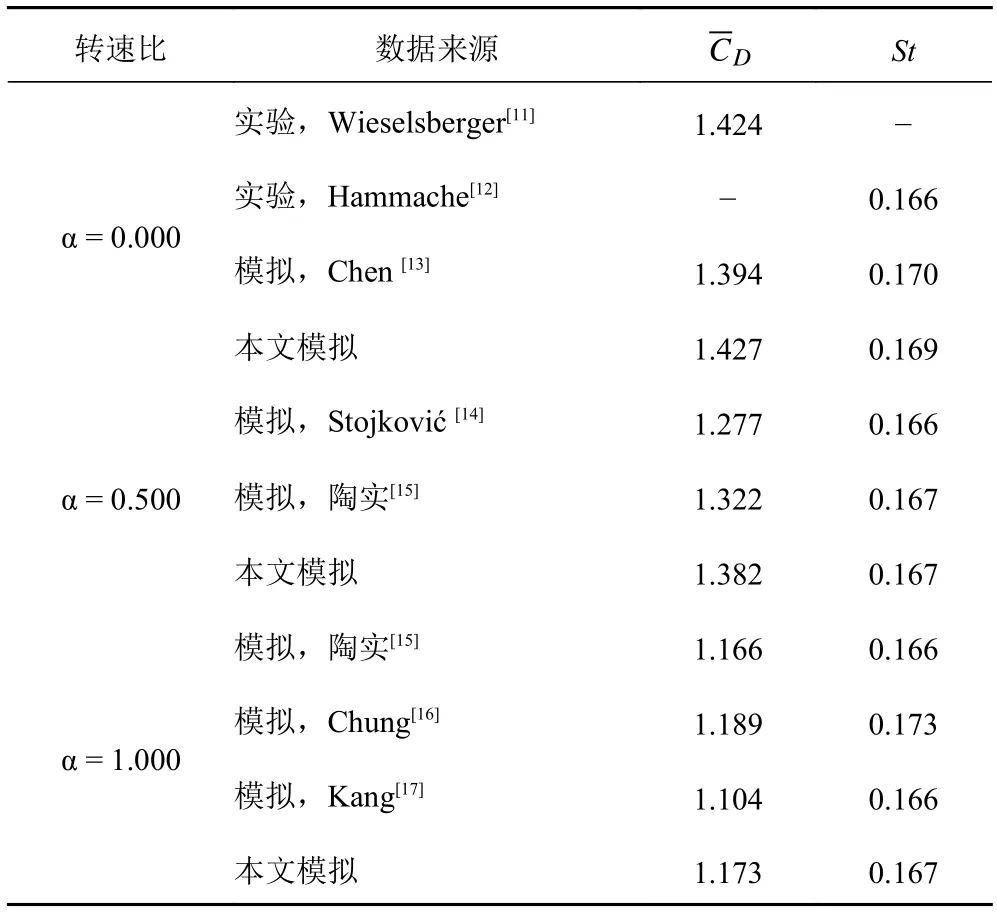
表1 模拟结果与参考文献结果对比Tab.1 Comparison of simulation results with others

由表1可知，静止状态时本文模拟所得平均阻力系数和St数与实验结果拟合较好，误差控制在2%以内。St数与同样采用模拟手段文献[13]的结果基本相同，平均阻力系数误差也小于3%。而当圆柱旋转状态时，本文模拟得到的平均阻力系数与文献数据依然吻合较好，与Stojković等模拟结果最大偏差为6.3%。同时，St数与参考数据基本相同，最大误差仅为3.5%。从而可知该自编程序对于模拟圆柱绕流具有良好的可靠性。

2 计算区域

圆柱直径D为流动特征长度，令两圆柱圆心距为L，如图2所示，计算区域为20D×50D，两圆柱距入口长度为10D，距出口长度为40D。

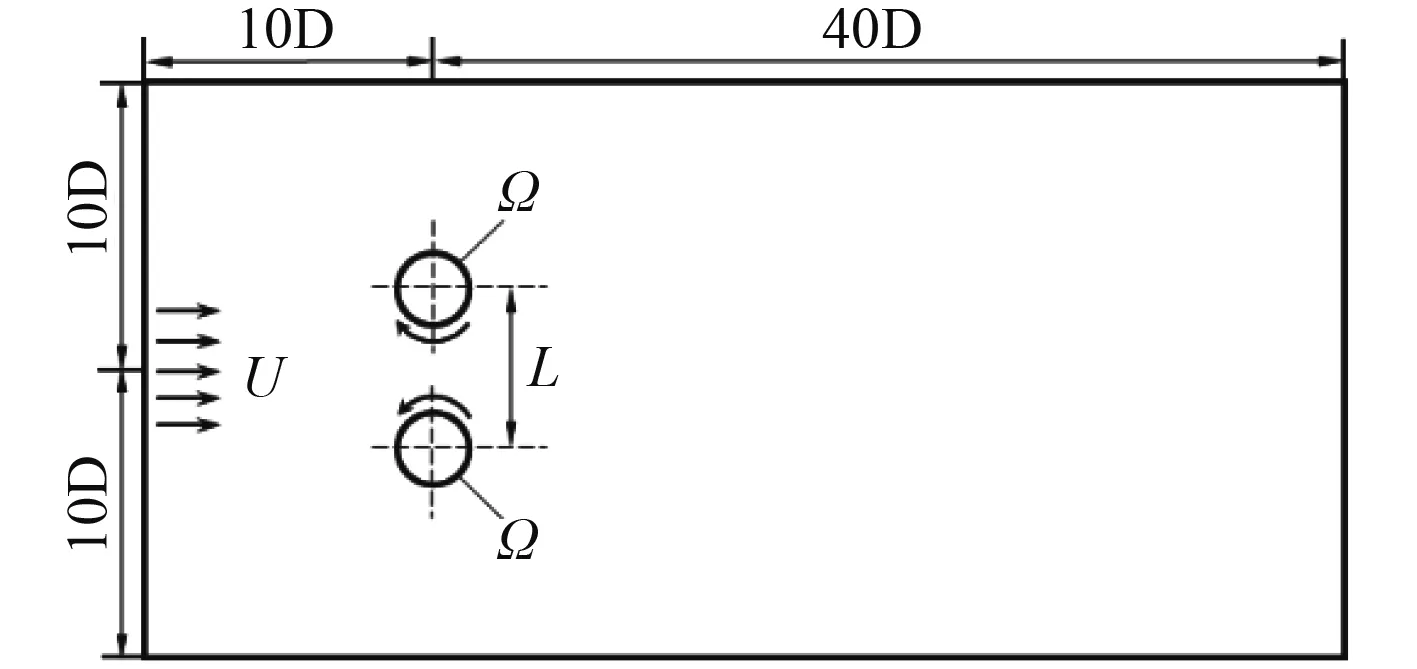
图2 计算域Fig.2 Computational domain

设置Re= 100，转速比|α| = 0.5，1.0，1.5 和 2.0，令上圆柱顺时针转动，下圆柱逆时针转动。选取L/D=1.2， 1.7， 2.5和4.0四个典型间距比。图中U为来流速度，流向速度和法向速度分别定义为u和v。上下壁面采用无滑移边界条件，进出口边界条件定义如下：

进口u=U=0.1，v=0;

出口∂u/∂x=0，∂v/∂x=0。

3 结果及分析

3.1 静止并列双圆柱

图3给出了不同间距比并列双圆柱在静止状态（|α|=0）下的升阻力系数变化曲线及对应的涡量云图。可以看到间距比对并列双圆柱绕流的尾流有明显的影响。从图3（a）中涡量云图可以看到，当间距比很小时，间隙流对圆柱后尾流几乎没有影响。在双圆柱的上下两侧交替生成漩涡脱落，并在其尾流只形成一个涡街。相应的流动稳定后圆柱升阻力系数随无量纲时间（t=tU/D，下同）呈现周期性变化。

随着间距比的增大（1.2＜L/D＜2.2），从图3（b）中可知间隙流对圆柱后尾流的影响增强，导致单涡街结构被破坏，尾流不再具有周期性，间隙流交替地偏向一侧，呈现出偏流模式，同时可见在两圆柱后形成宽的和窄的尾流结构。此模式下两圆柱的升阻力系数的变化不再具有周期性，可见两圆柱的阻力系数交替变化，间隙流偏向的圆柱其阻力系数较大。

当间距比持续增大（L/D＞2.2），由图3（c）和图3（d）可知尾流再次呈现出周期性，并且2列旋涡同步脱落，称为对称流模式。对称流模式又分为同步同相和同步反相。如图3（c）所示，对于同步同相模式，两圆柱表面形成相位相同的旋涡，在距离圆柱一段距离后，符号相同的涡会融合成尺度更大的涡，说明此时尾流中的涡结构是不稳定的。相应圆柱的升力系数随时间的变化曲线相位是相同的。而从图3（d）可见圆柱的升力系数变化曲线相位差180°，表明此时旋涡同步反相脱落。从涡量云图中可以看到两圆柱后缘生成同步反相的旋涡，在圆柱后同时存在2列关于流场中线对称的平行反相涡街。不同于同步同相模式的是此时2列涡街在很长一段距离内一直保持稳定，并且与单圆柱绕流的尾流结构相似。上述模拟结果与Sumner D.等[18]的结论相符。

图3 静止状态下不同模式的升力系数和阻力系数变化曲线及对应的涡量云图Fig.3 The curves of lift and drag coefficient of different modes under stationary state and the corresponding vorticity cloud diagram

3.2 旋转并列双圆柱

圆柱旋转将带动其周围流体一起运动，对于均匀来流的流场，将在圆柱两侧对流体分别产生正的和负的作用。根据马格努斯效应，由流速差引起的压力差将会在圆柱上产生与来流方向垂直的横向力。本文的并列双圆柱采用上顺下逆的对转方式，可知上圆柱的升力方向为垂直向上，下圆柱的升力方向则为垂直向下。从图3可见，对于不同转速比下上圆柱的升力系数大于零，而下圆柱的升力系数小于零，即上下圆柱所受升力方向相反，与上述分析结论相符，同时也表明此种对转方式两圆柱之间存在排斥力。

图4为间距比L/D= 1.7时，升力系数与阻力系数的变化曲线及对应的涡量云图。对比图3（b）和图4（a）可知，对于偏流模式，转速比增加到1.0时，圆柱后的尾流被拉长，并且在圆柱后出现单涡街流型，尾流由偏流模式转变为单涡街模式。同时从升阻力系数曲线图可以看到，在流动稳定后，圆柱的升阻力系数曲线呈现出周期性。当转速比增大到|α| = 1.2时，从图4（b）可以看到2个圆柱后尾流涡变得狭长并且不再有漩涡脱落，同时可以看到两圆柱的阻力系数几乎重叠以及升阻力系数曲线的脉动值近乎为零，流动稳定后的升阻力系数曲线接近一条直线，可知间距比为1.7时的临界转速比|αc| = 1.2。由图4（c）的涡量云图可以看得，当转速比进一步增大（超过临界转速比）时，两圆柱之间的间隙流被完全削弱，对尾流结构不再有影响作用，流场变得稳定不再有漩涡产生和脱落。升、阻力系数变化曲线的趋势与图4（b）一致。

图5给出了间距比L/D= 2.5时，升力系数与阻力系数的变化曲线以及对应的涡量云图。由前文可知圆柱静止时的流场为对称流中的同步同相模式，从图5（a）涡量云图可以明显看到当转速比为1.0时圆柱后的尾流呈现同步反相模式，从对应的升阻力系数曲线也可以得到证实。之后升阻力系数曲线以及涡量云图随转速比增大的变化趋势与间距比为1.7时相似。结合图4和图5可以知道，并列圆柱的旋转可以有效地抑制漩涡的产生和脱落，甚至彻底消除涡街的生成。间距比L/D为1.2和4.0随转速比变化而变化的趋势与上述两者类似。根据本次的模拟结果证实了不同间距下临界转速比的存在，对于选取的间距比L/D= 1.2，1.7，2.5和4.0，对应的临界转速比分别为|αc| = 1.2，1.2，1.3和 1.7。

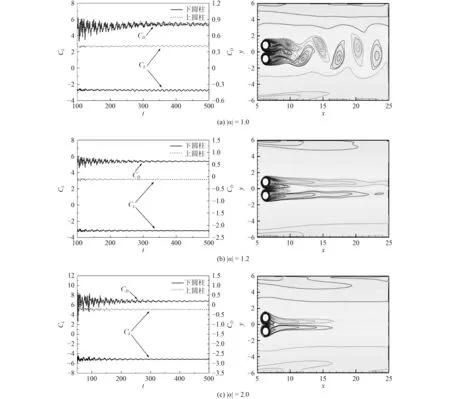
图4 间距比L/D = 1.7时不同转速比下升力系数、阻力系数的变化曲线与对应的涡量云图Fig.4 The curves of lift and drag coefficient and the corresponding vorticity cloud diagram at different speed ratios when L/D=1.7

图5 间距比L/D = 2.5时不同转速比下升力系数、阻力系数的变化曲线与对应的涡量云图Fig.5 The curves of lift and drag coefficient and the corresponding vorticity cloud diagram at different speed ratios when L/D=2.5

4 结 语

风力助推转子能够合理有效地利用风能，进一步完善船舶推进技术。本文基于格子Boltzmann方法，对不同间距比和转速比下的并列转子绕流进行了研究。文中主要对升力系数、阻力系数以及尾流流型等数据进行处理和分析，得出如下结论：

1）对于单圆柱，基于自编程序对静止和旋转状态分别进行了模拟，将结果与其他文献中的数据进行对比，验证程序的准确性。

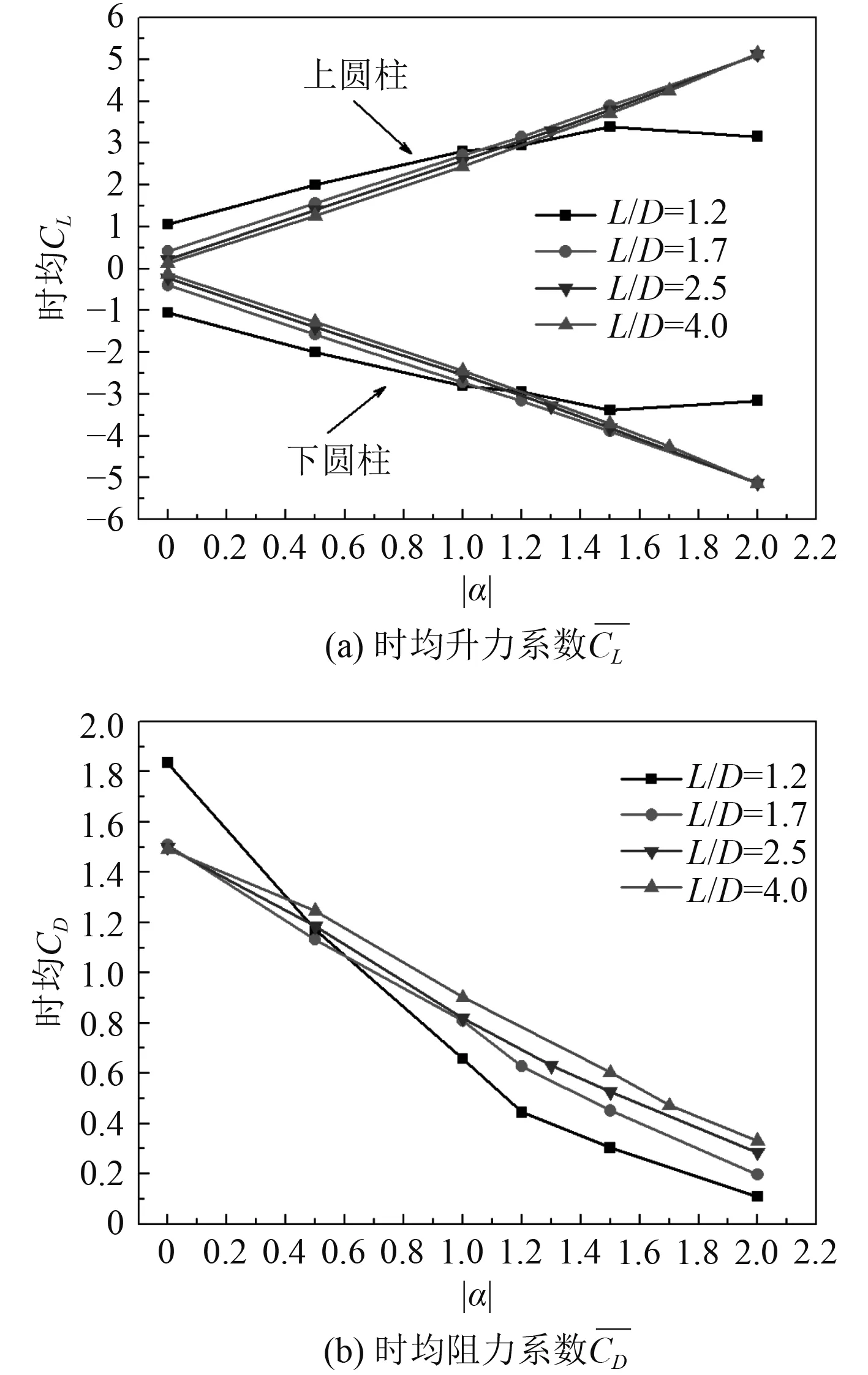
图6 不同间距比的时均升力系数和时均阻力系数随转速比的变化曲线Fig.6 The curves of the mean lift and mean drag coefficient with different rotational speeds at different spacing ratios

2）对于静止并列双圆柱，随着间距比的不同存在3种典型的尾流流型： 1.0＜L/D≤1.2时，单涡街流型；1.2＜L/D≤2.2时，偏流流型；L/D＞2.2时，同步对称流型，其包括同步同相和同步反相2种流型。

3）并列双圆柱的对转可以明显减轻间隙流对尾流的影响，同时也可以有效地抑制圆柱后涡的生成和脱落，并且当|α|达到临界转速比后，流场开始变得稳定，涡街随之消失，给出了不同间距比对应的临界转速比|αc|。

4）两圆柱时均升力系数的绝对值随转速比的增大而增大，而时均阻力系数则随着转速比的增大而减小。时均阻力系数的脉动值随着转速比达到|αc|后出现变小的趋势。