基于自适应变分模态分解的辐射源识别算法分析

2021-05-16吴俊

科学与信息化 2021年12期

吴俊

四川大学电子信息学院四川成都 610065

引言

特定辐射源识别根据其独特特征将单个发射器与其他发射器区分开，从而识别出不同的发射器[1]。特定辐射源识别技术主要用于军事通信中。随着新技术的出现，例如自组织网络和认知无线电，它变得越来越重要。

基于发射器的工作方式，特定辐射源识别可以利用瞬态或稳态信号[2]进行发射器识别。瞬态信号也称为开/关信号，它提供了适合于发射器识别的独特特性。要提取瞬态信号的特征，主要方法是通过检测噪声的起点和终点来提取瞬态信号。但是，瞬态信号的持续时间短且难以捕获。它容易受到复杂信道的干扰，并影响发射器的识别效果。稳态信号在整个信号的瞬态开始和结束之间传输。与瞬态信号相比，稳态信号的检测和采集更加简单。然而，由于稳态特征容易被破坏，使得稳态特征的提取变得困难。对于稳态信号，最常用的方法是基于时频分析算法[3]。

目前，提出基于经验模态分解（Empirical Mode Decomposition，EMD）来处理信号。接着，变分模态分解（Variational Mode Decomposition，VMD）[4]也应用于特定辐射源识别。众所周知，EMD算法对采样和噪声极其敏感，VMD算法有更好的鲁棒性。然而，VMD算法的输入参数是人为输入，而本文所考虑的主要问题是如何解决参数自适应，故提出一种基于AVMD的识别算法，与基于VMD和EMD的算法相比，该方法具有更好地识别性能。

1 系统模型

在辐射源信号生成过程中，功率放大器是主要影响因素，功放固有的非线性和记忆效应会使得信号非线性失真。这里我们采用非线性记忆多项式模型[1]来表示这种信号：

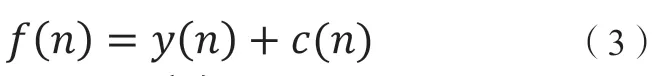
2 AVMD分解

与许多典型的分割方法类似，VMD需要预先知道它的输入参数。在VMD分解中，惩罚因子与分解层数是主要影响分解结果的因素。其中，惩罚因子影响分解精度。相比于分解模态数，只会影响到分解结果的精确程度，而值则直接影响分解结果是否正确，所以在此对K值进行深入研究。

针对以上问题，提出一种利用峭度来确定K值得方法。依次选取的整数，对原始信号序列进行VMD，经过VMD过后得到多个固有模态函数(intrinsic mode function，IMF)。选取相关系数最大的IMF作为最优模态。接着，计算最优分量的峭度，选取峭度最大时的值作为最优分解模态数。计算出时相关系数最大分量的峭度，并绘制峭度变化曲线，若在该曲线上没有峰值且单调递增，则继续计算当K为是的相关系数最大分量的峭度值，重复以上步骤。以峭度最大为优化标准，当峭度最大时，K为最佳选择。我们将AVMD的算法流程表示为

3 分类算法

本文提出的算法通过测量希尔伯特谱的偏度(Hilbert Spectrum skewness，HS)来提取特征。首先，对进行希尔伯特变换；接着，提取希尔伯特谱的偏度作为识别特征；最后，送入KNN分类器。偏度可以统计数据分布非对称程度，表示如下：

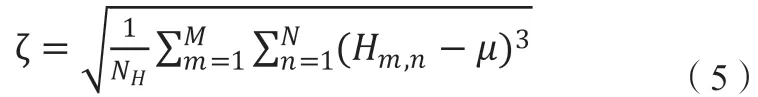
训练阶段：辐射源类数P，每类数量

（1）原始信号经过AVMD，得到K个IMF分量；

（2）对各个IMF进行希尔伯特变换，求得希尔伯特谱；

（6）测试序列并没有标签，利用训练阶段的KNN分类器对测试序列进行识别。

4 实验分析

在本小节中，我们通过各种数值实验对所提出的算法进行性能评估，以正确识别率作为性能度量标准。辐射源信号的调制格式为4QAM，采样频率10GHz，载波频率2GHz，每个时间序列为500个采样点，序列时间为50，系统模型的记忆效应偏移为，多项式阶数，所采用的非线性系数分别为：，。

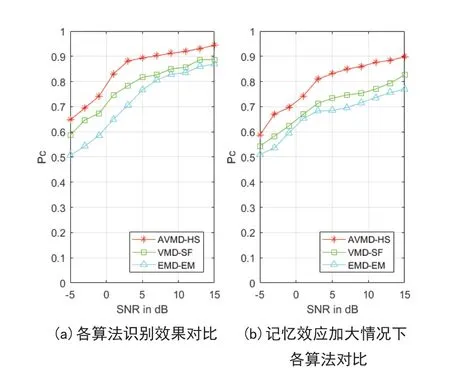
图1 算法对比图

将本文所提算法与文献[4]算法进行比较。VMD-SF算法设置。我们将AVMD-HS算法、VMD-SF算法EMD-EM算法进行对比。实验结果如图1(a)所示，AVMD-HS算法的平均识别率比VMD-SF和EMD-EM分别高出6%、10%，当AVMD-HS算法在信噪比高于0dB时，识别率就会达到80%，而VMD-SF算法和EMD-EM算法则需要信噪比分别高于3dB和7dB。低信噪比时，EMD-EM识别效果下降更为明显。接着，加重记忆效应，以此来增加识别难度，将记忆效应的时间偏移增加为0.3。实验结果如图1(b)，我们可以看出，当记忆效应加重的情况下，VMD-SF算法和EMD-EM算法识别率下降严重，平均下降了7.3%和6.6%，而AVMD-HS平均识别率只下降了5.4%，并且在3dB时，识别率超过了80%，达到了有效识别的程度。

综合对比来看，AWMD-HS算法无论是在识别效果，还是抗记忆效应的效果，都要优于VMD-SF算法和EMD-EM算法，具有更强的鲁棒性。