基于大数据与神经网络的道路拥堵优化技术与实现
2021-05-16肖权珈任绍坤杨锦涛
肖权珈 杨 杰 任绍坤 杨锦涛
(中南大学,湖南 长沙410083)
1 研究现状
在交通拥堵优化方面,主要从以下几个角度做了重点研究。
1.1 城市规划角度,如:交叉口合流冲突点改进[1]通过设置立交桥、人行通道,加强交通管理,优化公交站台等方式,可以有效的解决合流、分流路口的严重冲突问题;或者适当控制城市扩规模,适当发展卫星城[2]着重利用卫星城来疏解大规模城市的部分功能。尤其分担大城市的交通压力。
1.2 从交通控制角度:基于人车流量组合来控制红绿灯[3]即将摄像或影像采集设备所接受到的实时交通信息,包括人流、车流、障碍物等信息传递到数据计算终端,通过数据模型计算和远期评估,确定不同道路区域的人流量和车流量。并结合现场人流车流的情况以及通行速度,预估各个路口所需的通行时间,并确定整体的最优通行策略,从而形成不同人流量和车流量的路口,分配不同的红绿灯通行时间,确保道路通行顺畅,提升道路通行效率。
1.3 根据公交流,应用BP 神经网络预测城市短时交通流量。[4]另外可以运用物联网技术的应用[5],即通过车联网技术的应用,使得车辆及时通过车载设备及显示终端,获取云数据平台所展现并计算的路况和通行信息,保证出行车辆及人员能够合理规划自身的出行方案,缩短出行的时间,提升出现效率,并且也能够避免某个城市点位的大量拥堵产生。
2 道路拥堵解决方案
2.1 数据处理
对车流量进行预测依据的交通数据分为两种:
2.1.1 历史的交通数据。对历史交通数据进行预处理后,再进行分析,可以得到路口的拥堵时段以及车流量规律等信息。基于历史交通数据,进行初步预测。
2.1.2 路口实时采集的交通数据。我们根据路口实时采集的信息,可以对初步的预测结果进行修正。以上两种不同来源交通大数据具有共同特点。按相关交通数据的类型和采集方式的不同,可以形成比较规范的数据集,主要包括:长期交通流量数据、瞬时交通车流数据、道路最大承载能力数据、通行时长数据、交通指示指令数据以及交通调度服务数据等;交通流量数据的重要参数包括:速度、流量、密度、起止时间、时间平均速度、空间平均速度等;
由于各种原因,如设备老化,道路结构破坏等,使得我们采集的数据常常出现异常值、冗余值、缺失值等等错误数据;而且在实际监测过程中也会出现数据丢失或者数据冗余的情况,所以需要进行数据清洗。
使用低阶多项式滑动拟合法来识别错误数据:
时间序列表示为x(t)(t=1,2,3……n),则拟合多项式为m 阶自回归多项式:

以上滑动拟合并识别错误数据的主要方法是通过测算数学期望值,并评估置信度来判断数据是否符合置信度区间,并确定数据的错误与否。以时间序列进行计算X∧i,以及数学期望ζ=Xi-X∧i,错误数据与正常数据相比,它的信息值比正常值大的多,使用公式:
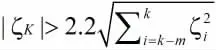
以低阶多项式来大致判断错误数据,为了简化过程我们把所有错误数据剔除,然后结合该道路的路段信息,如路况、限速等,就可以由交通流量数据中的时间平均速度,实时判断该路段是否发生拥堵。
2.2 BP 神经网络预测模型
BP 神经网络是目前应用最广泛的一种人工神经网络之一,它是一种多层前馈网络,包含输入层、隐含层和输出层,同层单元之间不相连,它在输入层和输出层之间可有一个或多个隐含层。
从输入层的特征来看,输入层的神经元主要是根据样本的不同属性和类型综合确定神经元纬度,输入层要确保充分考虑到所有数据纬度及相关属性的准确性。从隐藏层的特征来看,隐藏层主要是由用户提供的数据阈值及相关条件组成,隐藏层作为重要的限制条件,能够改变神经元的活性,保证预测模型的灵活性和可变性。前一层神经元和后一层神经元之间有权值。每个神经元都有输入和输出。输入层的输入和输出都是训练样本的属性值。
BP 神经网络的结构较为简单、易于硬件实现、并且工作状态稳定,有许多优点。包括有自学习与自适应能力,可以简化预测难度以及实现对大量数据进行处理等。交通数据非常庞大,BP 神经网络能达到对大量且复杂的数据的一个较为精确的处理。因此,选用BP 神经网络进行预测。
2.3 存储一转发模型(TUC 策略)
根据基本的存储一转发模型来进行车辆调度,就是当车辆按照既有的路线行进时,如果道路中的实际车流量超过该段道路所能承载的最大车流量(饱和值),车辆就需要提前停止行进并在相应路口等待,直到当前方道路车流量恢复平稳或者能接受新入车辆后,等待路口的交通信号灯再做出改变,引导车流通行。
从实际看,存储- 转发模型是一个相对简单的交通模型,通过存储- 转发的机制,将道路和车流调配分解为两个简单的节点,在运用此模型时,我们假定建输出流为u,如果道路路况及车流都能满足相应条件,输出流u 在某一个时间段内可以使用下边的公式表示:
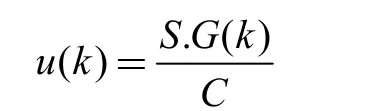
S 为相关道路中的最大车流承载能力和承载量,G 是可通行的交通信号灯持续时间,C 是相应路口红绿灯所需的一个周期时间。由于每个阶段时间T 应该与离散时间C 相等。u 为在每个阶段时间T 中的平均车流量,而不是在红灯时间的0 或者绿灯时间的饱和车流量S。换句话说,假设每个车道车流量是连续不间断的,从存储- 转发模型可以得出以下结论:
(1)每个阶段时间T 应该与离散时间C 相等。
(2)没有描述红灯时间或者绿灯时间车辆排队情况。
(3)不能连贯的表示每个十字路口每个相位的情况。
当然,为了避免这些冲突和复杂情况的出现,一些非线性规划、二次规划等高效优化方法也应运而生,并可通过这些方法来协调复杂的交通网络问题。
3 交通拥堵优化实现
在实现之前,定义了一部分假设,而这些假设都是在道路中车辆不饱和的情况下存在的,得到的绿灯时间是基于历史需求而得出的。通过绿灯时间来控制网络达到最优状态并且道路中车辆排队数量为零。然而,在现实中,车辆的数目是动态改变的。所以,如何确定绿色时间的值可能是最优,并且可以控制交通情况比较恶劣的交通状况。
通过LQ 方法来实现最小化性能标准,LQ 方法的控制法则为:
g (k) = gn-L. x ( k )
通过实验模拟及数据仿真可以得出,增益矩阵L 对道路车流量数据变化所产生的变化较小,相应敏感度角度,尤其是在转弯率与最大饱和流量变化时更加明显。gN 为理想状态下假设的最优时间。L 为常量反馈增益矩阵,L 是由A, B, Q, R 共同决定的,矩阵的规范如下:
(1)控制间隔:在选取并存储- 转发策略时,根据实际需要,应该对每个控制点的时间进行规范和控制,无论是控制时间间隔太长或者太短,都不利于得出精确结果。因此结合大多数路口及城市实际交通控制情况,将时间间隔设置为90 秒。
(2)道路的数量:交通网络中道路的数量对TUC 策略中LQ方法的应用产生影响。
(3) 相位:交通网络中十字路口的相位对TUC 策略中LQV方法的应用具体重要影响。
(4)每个道路的v:以四个相位的十字路口为例,驶入与驶出相同路口的车流导向图也具备相同的规律。(如图1、图2)
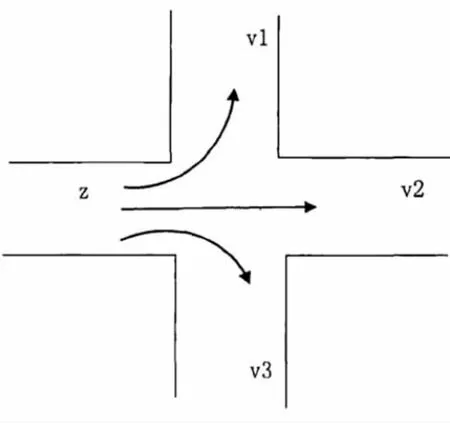
图1 驶入道路Z 的车流导向
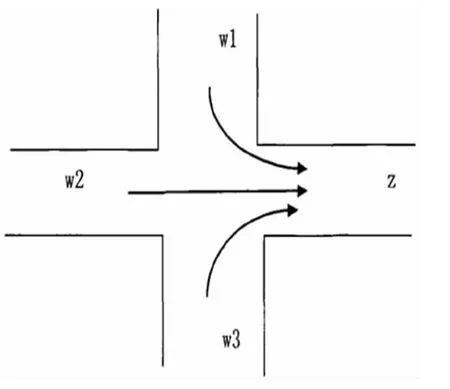
图2 驶出道路z 的车流导向图
(5)每个道路的S:测算道路的饱和流量,一般需要结合实际路段的特定情况,包括限制车速、道路宽度、道路长度、当地的执行标准等得出。
(6)t:这里是指每个道路路口车辆的转弯率,按照相关设定以及实际道路通行的情况看,此数据对LQ 方法应用具有较大影响。
(7)R:R=rI,由试错法得出,我们取r=0.00050。
(8)Q:Q 是考虑到每个链路上车速不同,长度不同而提出的因子,致使每个链路都达到最优,Q 的取值为对角线为每条链路的最大值的倒数,其他元素都是0 的矩阵。
由于gN为理想状态下假设的最优时间,所以可列公式:
g ( k ) = g ( k - 1) - L *[ x (k ) - x( k-1)]
g(k-1)为k-1 阶段有效绿灯时间,x(k-1)为k-1 阶段道路中的车辆数,g(k)为k 阶段有效绿灯时间,x(k)为阶段道路中的车辆数,L 为状态反馈矩阵。
4 结论
智慧城市是未来城市发展的趋势,而智能交通是智慧城市的一个重要组成部分,也是一个研究的热点。以计算机技术为主,综合了交通学科的相关理论。运用互联网+的思维,为传统的交通领域赋能。通过运用了神经网络进行预测,与传统的预测方法相比较,对信息源准确度要求不高,有较好的容错能力。与以往的交通调控相比,加入了用户与交通控制系统之间的“互动”,形成一个正反馈机制,并将大数据技术结合交通领域相关知识,对信号优化和路径规划都建立了相关的模型,在智能交通方向做了一些探索,且成果也可运用到无人驾驶系统中去。
