基于OWA 算子改进模拟退火算法的路线规划研究
2021-05-16赵人行郭旭萌霍俊生赵景林
赵人行 郭旭萌 霍俊生 赵景林
(1、北京邮电大学 经济管理学院,北京100876 2、成方金融信息技术服务有限公司,北京100120 3、方正国际大数据(北京)有限公司,北京100080 4、黑龙江省科学技术协会,黑龙江 哈尔滨150001)
1 概述
运筹学与工程系统分析中的行程选择与设计问题,是数学领域内行程路线最优化的典型问题。我国旅游线路设计研究经过十几年的发展己经初具研究成果,研究角度涉及地理学、经济学、运筹学等领域,但研究深度还不够,实证研究多,理论研究少;一般描述多,深入分析少。目前结合旅游景区相关条件和交通工具的研究多为按照国界、旅游天数、旅游线路距离远近、旅游活动内容和性质、乘坐交通工具、行为和意愿特性,综合性旅游路线规划还很少,研究对于数据的利用和挖掘还不够充分。我们必须尽可能利用相关数据开展研究,同时对相关的新课题进行探索性研究。本文是根据国家旅游局公布的5A 级景区及相关信息和省会城市间道路信息,及《全国高速公路一览表》中现阶段交通道路情况,提出一个典型热点问题:最佳出行方式的选择,研究旅游路线的具体策略和方案。随着各种旅游服务业的发展,出行方式还可以考虑乘坐高铁或飞机到达与景区相邻的省会城市,而后采用租车的方式自驾到景区游览。依据数学模型,设计一个十年游遍所有201 个5A 景区、费用最优、旅游体验最好的旅游线路,给出每一次旅游的具体线路(含每次具体出行方式;每一天的出发地、费用、路途时间、游览景区、每个景区的游览时间。租车费用300 元/天,油费和高速过路费另计,租车和还车需在同一城市)。此种出行方式可以节省一些路途时间用于景区游览或休闲娱乐,但这种出行方式也会给旅游者带来一些不便,有时费用也会增加。旅游爱好者根据个人旅游偏好确定在每一个景区最长逗留时间不超过统计数据给出的最少时间的2 倍。若干城市之间的高铁票价和相关信息(约定:选择高铁出行要求当天乘坐高铁的时间不超过6 个小时,乘坐高铁或飞机的当天至多安排半天的景区游览);若干省会城市之间的机票全价价格信息(含机场建设费)。设旅游爱好者一家3 人同行,综合考虑前述全程自驾、先乘坐高铁或飞机到达省会城市后再租车自驾到景区等出行方式(住宿费简化为省会城市和旅游景区200 元/人·天,地级市150 元/人·天,县城100元/人·天;高速公路的油耗加过路费平均为1.00 元/公里,普通公路上油耗平均为0.60 元/公里。各景区所在地的信息,若景区位于某城市市区或近郊,则这类景区的市内交通费用已计入住宿费中,不再另计)。
2 模型假设与问题分析
2.1 模型假设和符号说明
2.1.1 模型假设。2.1.1.1 旅游的过程中选用的任何交通方式不受恶劣天气、交通拥堵、突发事件等干扰因素的影响。2.1.1.2旅游方案中设计的所有高速公路都可以双向行驶。2.1.1.3 城市到景区、景区到景区的公路均为普通公路。2.1.1.4 G75 兰海高速琼州海峡段以高速公路形式连通。2.1.1.5 租车自驾旅行过程中人和车全程需在同一城市内。2.1.1.6 旅游者一家三口出游,三人住宿费以三个单人费用标准计算。2.1.1.7 旅游者一家三口出游,乘坐高铁飞机费用均为全价成人票,不存在学生票和临时优惠情况。2.1.1.8 旅游者出游,旅途中所有住宿费计算均以整天为单位。2.1.1.9 国家4A 级景区游览时间为0.5 天。
2.1.2 符号说明,见表1。

表1 符号说明
2.2 问题分析及数据采集
2.2.1 问题分析。以高铁、飞机、租车与自驾4 种交通方式相结合的全国5A 级景区综合旅游线路规划。2.2.1.1 交通方式增加了高铁和飞机之后,可以有效地解决省会之间远距离、长时间驾驶的问题。根据自主收集了更为全面的全国高铁和航班信息。使用Floyd 算法求解上述任意两个省会城市之间的最短高铁和航班路线。经过对最短路径矩阵和路由矩阵的分析可得,任意两个省会城市之间均有直达航班或转机航班,但是部分西部省份省会城市未通高铁。2.2.1.2 题目指出了省会之间更为便捷的交通方式和异地租车旅游的思路,大大缩短了省会之间的交通代价和对自驾游的限制,也加大了省会城市之间和普通城市之间交通便捷程度的差异。本文利用这一差异,使用分治算法将整个国内5A 级景区旅游线路规划问题分解为多个省会及附近5A 级景区线路规划的子问题。[1]由题设和分治算法可知,总问题与子问题性质相同,解结构相似,子问题之间相互独立。求出所有子问题的解,就可以得到总问题的解。2.2.1.3 建立数学模型设计一个十年游遍所有201 个5A 景区、费用最优、旅游体验最好的旅游线路。这一要求中包含一个定量条件,即十年内遍历201 个5A 级景区和两个定性条件,即费用最优、旅游体验最好。两个定性条件没有具体要求,比较模糊。使用OWA 算子(有序加权平均算子),明确可定量的评价因素,对使用模拟退火算法生成的有限旅游方案属性值进行集结和评价,给出指定评价体系内的近似最优解。
2.2.2 数据采集。2.2.2.1 全国公路道路数据收集。过全国最新高速公路里程表,以及互联网数据得到城市与景区之间的具体数据。道路数据分为两部分,第一部分是城市之间的距离,第二部分是城市与景区、景区与景区之间的距离。第一部分道路数据,由全国高速里程及途径城市一览表获得。数据采集规则是:与某一城市经高速公路直接相连的其他所有城市,均被计入该城市的邻接表中。此外利用互联网收集到全国主要城市之间的高速里程以及对应行驶时间。第二部分道路数据由官网查询得到。《全国部分景区公路道路数据整理》,收集到201 个国家5A 级景区和相关城市的高速里程数据。2.2.2.2 全国高铁及航班数据收集。见《全国部分省会航班航行时间简表》和《全国部分省会高铁运行时间简表》。2.2.2.3 景区数据分析。根据《全国各省份5A 级景区分布图》,了解到201 个国家5A 级景区的分布信息。5A 级景区在华北、华东地区分布较为集中。江苏省5A 级景区最多,有19 个,其次为浙江省,有12 个。同时,西部省份景点较少,且地理上分布较为稀疏,两两之间距离较远。
3 模拟退火模型的建立与求解
3.1 模拟退火算法
假设有一个旅行商人要拜访n 个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
此种情况下我们可以利用模拟退火算法来解决TSP 问题。TSP 问题是典型的NP 问题,本题题设要比普通TSP 问题复杂,因此是比较典型的NP-hard 问题(图1)。
对于这一NPH 问题,采用以概率1 获取全局最优解的模拟退火算法求取近似最优解,然后在多项式时间内进行结果的验证。对于NP-hard 问题,用一句话概括他们的特征就是NP-hard问题至少和NP 问题一样难。故可把本问题的定性分成两个部分,一部分可以用多项式的时间验证一个代表答案是不是真正的答案,这一部分问题组成了NP-complete 集合。证明一个问题是NP-hard,常用到的归约(reduction),通常用<=这个符号来表示,如P<=Q,这个就表示可以把P 归约到Q,当我们要证明一个问题是NP-hard 的时候,通常要做的是找到一个NPC 问题,把这个NPC 问题归约到NP-hard 上去,即NPC<=NP-hard。归约主要步骤为:(1)把NPC 的输入转化到NP-hard 的输入,即每一个NPC 输入,实际上都是一个NP-hard 的输入。(2)说明针对一个NP-hard 的输出,就能给出一个NPC 的输出。要证明此问题是NP 问题可通过归约。TSP 问题是典型的NP-hard 问题,因此此问题是NP-hard 问题。TSP 旅行商问题通过以上两个主要步骤可以归约到这个问题上来,并且以上的两个转化都要在多项式的时间内完成,旅游路线的规划和设计也是NP-hard 的。把任何一个NP-hard 的问题归约到最短公共超序列问题上来,就能证明最短公共超序列问题也是NP-hard 的了。[3]
3.2 基于模拟退火算法模型的求解
对于问题中的理想旅游方案有以下条件:
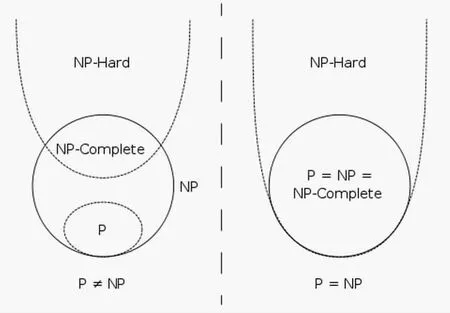
图1 P,NP,NP-hard,NPC 问题的关系
3.2.1 每年外出旅游时间不超过30 天,每年外出旅游次数不超过4 次;
3.2.2 每个5A 级景区有最少游览时间;
3.2.3 行车时间每天限于7:00 至19:00 之间,景区游览每天限于8:00 至18:00 之间;
3.2.4 每天驾驶时间不超过8 小时;
3.2.5 全天游览限制驾驶时间不超过3 小时;
3.2.6 半天游览限制驾驶时间不超过5 小时;
3.2.7 高速公路上的行车平均速度为90 公里/小时,普通公路上的行车平均速度为40 公里/小时;
3.2.8 各省省会均有24 小时的游览时间,不包含市区的景区。根据这些限制条件,使用matlab 编程实现,初始旅游方案和随机线路的旅游方案。初始方案用于模拟退火算法的最优值初始化,使用先近后远原则生成近似最优解的方案。随机线路方案用于模拟退火算法进行循环最优解的选择。每次生成一个随机序列,包含所有景区和省会,使用贪心算法及每次出行旅游都尽可能的去最多的景区,最后得到一个完整的旅游线路。由于景区序列是完全随机的,所以需要比较多的迭代次数来保证结果可以逼近最优解。在模型实际求解过程中,使用了如表2所示的参数控制退火过程。[4]

表2 模拟退火算法参数
其中,由于此问题的解空间十分巨大,所以为了使降温过程尽量均匀、缓慢,使用了如表所示的参数。
基于模拟退火算法的旅游路线规划算法流程如图2 所示。
3.3 数据处理
3.3.1 高铁或动车最短距离矩阵
31 个省会之间高铁或动车行车时间数据表,部分数据如表3。
3.3.2 航班最短距离矩阵
31 个省会之间航班行驶时间表,部分数据如表4。
3.3.3 5A 级景区分治数据
分治算法中,省会与景区分治分布部分数据如表5。
4 基于OWA 算子的多属性决策方法
4.1 基于OWA 算子的多属性决策方法及其基本思想
为下文论述,本部分令 M= {1,2, …, m},N = {1,2, …, n}。

图2 模拟退火求解算法流程图
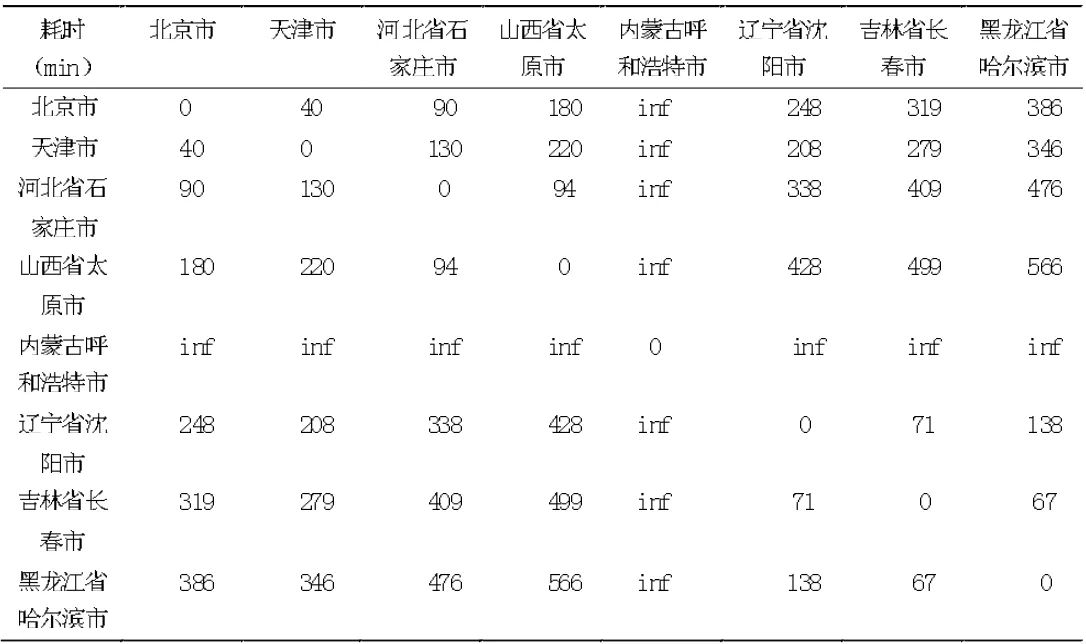
表3 高铁或动车最短运行时间数据简表
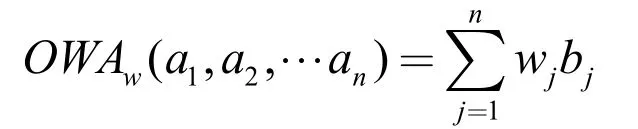
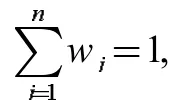
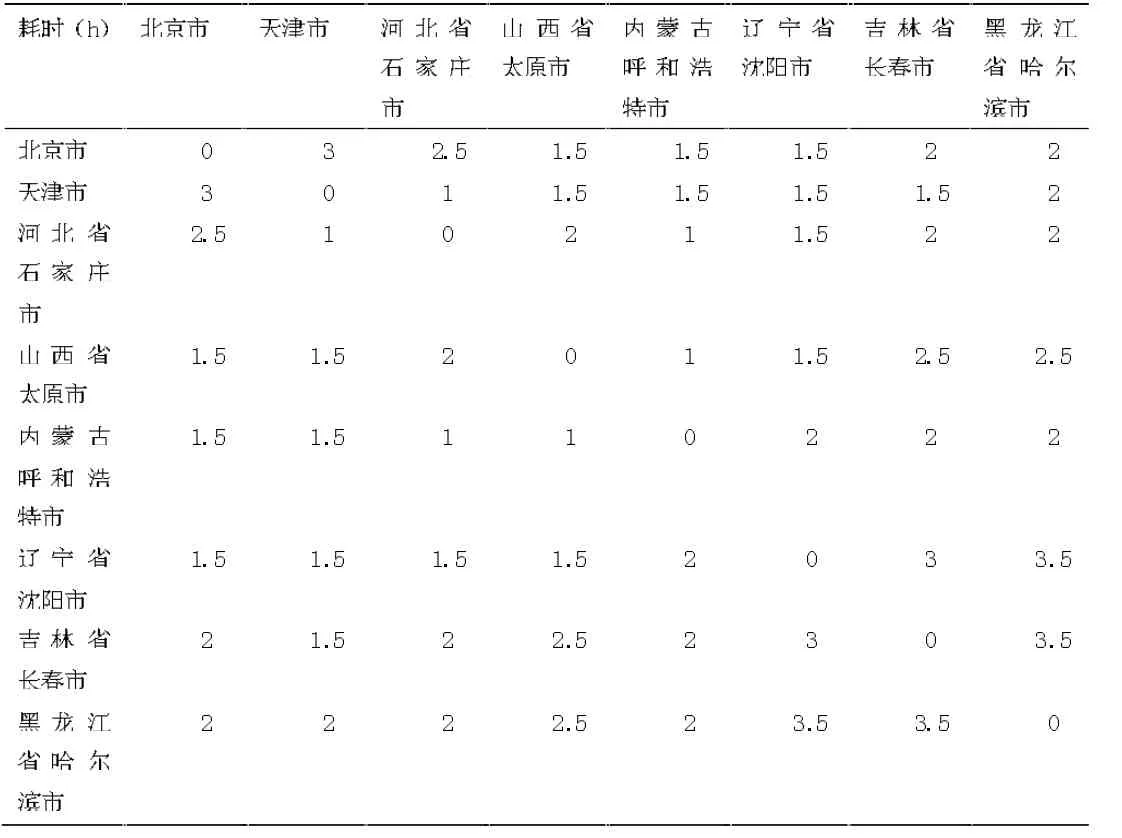
表4 航班最短运行时间数据简表

表5 省会与景区分治分布数据简表
OWA 算子的特点在于,对数据 ( a1, a2, …an),按从大到小的顺序重新进行排序并通过加权集结,而且元素aj与wj没有任何联系,只与集结过程中的第j 个未知有关(因此加权向量w 也成为位置向量)。[2]
4.2 基于OWA 算子多属性决策方法具体步骤


表6
本文中要针对初始最优方案以及随机方案的两个旅游方案x1,x2进行比较,并抽取下列9 项指标(属性)进行评估:
u1-旅游总支出;u2-旅游行车交通费占总支出比重;u3-旅游高铁飞机交通费占总支出比重;u4-旅游省会景区住宿费占总支出比重;u5-旅游市县住宿费占总支出比重;u6-旅游总时间;u7-旅游行车时间占总时间比重;u8-旅游高铁飞机时间占总时间比重;u9-景区游览时间占总时间比重;u10-旅游租车次数。


5 模型结果分析与验证
5.1 模型结果分析
本文的研究内容主要解决了在租车、高铁、飞机多种交通工具可供选择的情况下,根据旅游爱好者的出行习惯和偏好,设计和规划旅游的路线问题。
该模型中首先使用Floyd 算法求解任意两个省会城市之间的最短高铁和航班路线。利用省会之间高铁和飞机等更为便捷的交通方式和灵活的异地租车旅游的思路,大大缩短了省会之间的交通代价和对自驾游的限制。在旅游线路的规划上使用分治算法将整个国内5A 级景区旅游线路规划问题分解为多个省会及附近5A 级景区线路规划的子问题。
5.2 模型结果验证
对旅行路线的评价上使用OWA 算子(有序加权平均算子)方法,对使用模拟退火算法生成的有限旅游方案属性值进行集结和评价,最后给出指定评价体系内的近似最优解。以结果的方案的一次出行线路为例简表,如表7。
该次旅行路线为:
西安——昆明——迪庆藏族自治州香格里拉普达措国家公园——丽江玉龙雪山景区丽江古城景区——中科院西双版纳热带植物园——昆明石林风景区——大理崇圣寺三塔文化旅游区——昆明——西宁——青海湖风景区——西宁市湟中县塔尔寺景区——西宁——西安。分析该旅行路线得:该算法模型设计和规划的旅游路线首先从距离西安比较近的景区开始,然后逐渐向较远的景区扩展。每次旅游的景区相对比较集中,避免因景点之间的距离太远而造成来回奔波。模型规划的旅游路线节省了出行路上的时间成本和经济成本,提高了旅游者对旅游路线的满意度。单次出行的总时间适中,既避免了旅游时间过长而造成的旅途劳累,同时又不会因为旅游时间短而达不到调节生活的目的。通过分析生活和旅行习惯,及以上结合Floyd 算法和模拟退火算法并根据题目条件,使用OWA 算子对模拟退火产生的方案进行了评价。优化的算法流程,得到旅游花费总时间为271.5 天左右,共计出游20 次,预计10 年内完成游遍所有5A 级景区的旅游计划。总费用大约为30 万元。
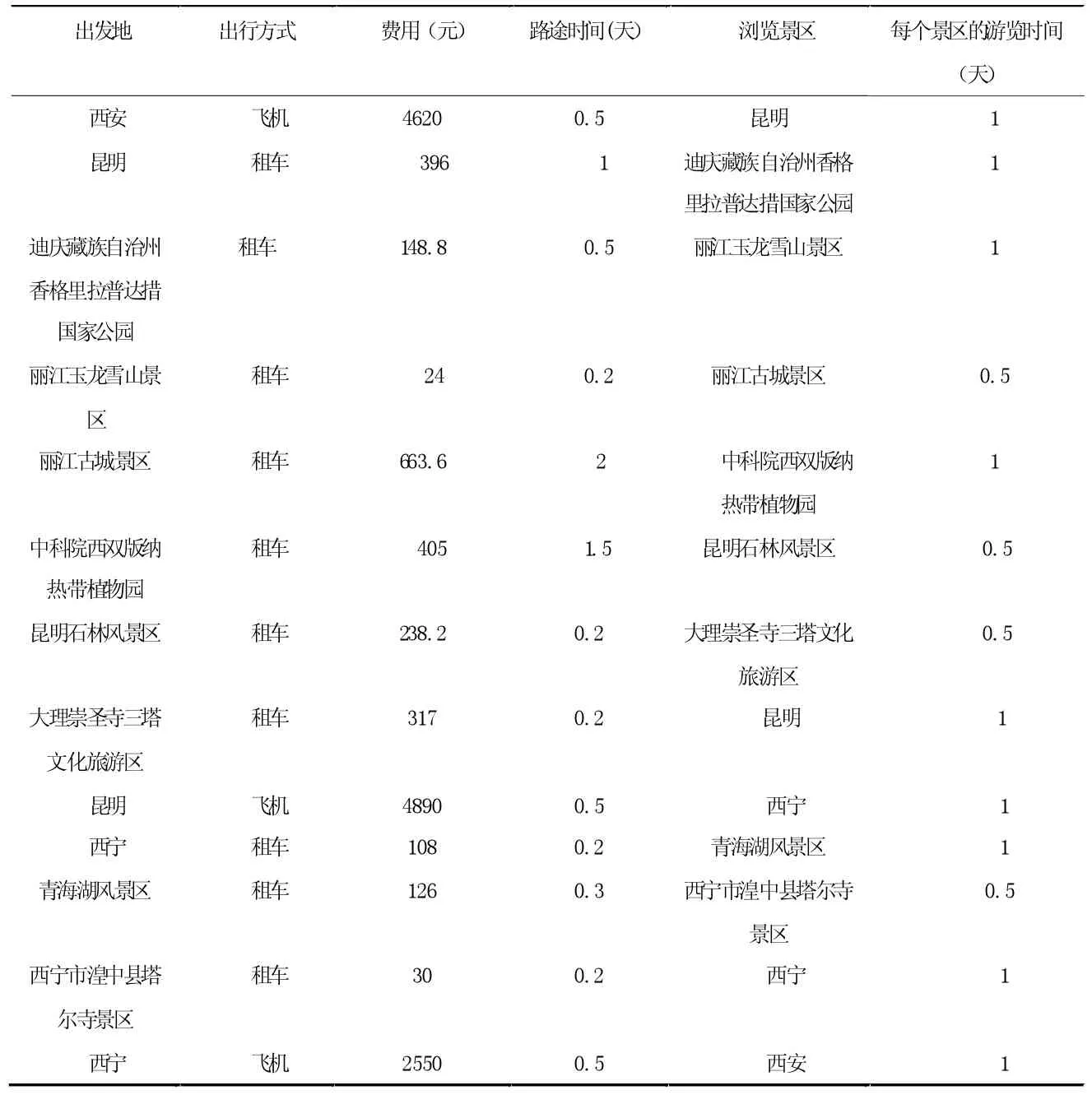
表7 出行线路
5.3 模型推广可行性分析
本文研究问题的模型是基于Floyd 的任意两点之间的最短距离优化算法,且通过模拟退火方法在对TSP 问题求解的基础上进一步优化,实现了方案寻优,并通过OWA 有序加权平均算子对方案进行进一步评价,故该模型不受出发地点影响,或其他因素影响可以忽略不计,可以推广为对全国的自驾游爱好者的旅游线路规划。通过对于个人自驾偏好的设置,可以为全国的自驾游爱好者规划设计类似的旅游线路,并以北京为旅游出发地进行旅游路线规划,并提供相应的旅游计划。
5.4 模型推广过程
本文问题的研究在评价函数中OWA 有序加权平均算子的应用基础上,对于自驾游爱好者,将设定的九个相应属性的类型进行调整,以符合“自驾游”的个人旅游偏好,对模型进行改进,以推广到全国自驾游爱好者的旅游路线规划模型中。针对初始最优方案以及随机方案的两个旅游方案x1,x2进行比较,并抽取下列9 项指标(属性)进行评估:u1-旅游总支出;u2-旅游行车交通费占总支出比重;u3-旅游高铁飞机交通费占总支出比重;u4-旅游省会景区住宿费占总支出比重;u5-旅游市县住宿费占总支出比重旅游总时间;u6-旅游总时间;u7-旅游行车时间占总时间比重;u8-旅游高铁飞机时间占总时间比重;u9-景区游览时间占总时间比重;u10-旅游租车次数。根据旅游者的自驾游偏好,将属性的类型进行调整,调整后结果为:其中成本型属性包括:u1,u2,u3,u5,u6,u8。效益型属性包括:u4,u7,u9,u10。在5.4 中,对于不同方案的九种属性进行数据规范化中,需将属性的类型针对旅游者个人偏好进行调整,以使相应的属性类型符合具体情况,为具有相应个人偏好的旅游者提供更好旅游体验的旅游路线规划。其他步骤以及评价函数应用大致相同,只需要更改与全国自驾游爱好者偏好相关的属性类别就可以将模型进行进一步推广。
5.5 方案合理性分析
由于OWA 有序加权平均算子,数据按从大到小的顺序重新进行排序并通过加权集结,而且元素与加权向量没有任何联系,只与集结过程中的大小位置有关,故当旅游偏好改变时,可以通过提取不同属性指标值,对属性的效益型和成本型进行调整,从而规划出更符合旅游者偏好的旅游路线。
6 模型的评价与推广
6.1 模型评价
6.1.1 模型的优点。6.1.1.1 模型运用分治算法,把本问题定性为NP-hard 问题,运用Floyd 求得最小距离矩阵,运用模拟算法进行方案寻优,具有较强的科学性。6.1.1.2 本文对于以时间为目标,以费用为最低,以旅游体验为目标的模型建立,充分考虑了所有可能对于旅游路线最优化的影响因素。
6.1.2 模型的缺点
本文问题中的旅游路线规划模型的求解结果中,评价算子的加权向量还可以通过数据以及组合数、三角函数等方法进行进一步优化。使得结果得到进一步优化,与收集数据具有更强的联系。
6.2 模型改进
模型改进中,可以考虑使用遗传算法或者神经网络算法对模拟退火算法进行相应优化,在评价方面通过组合数、三角函数、结合数据等方法,通过更全面的数据收集及数学方法的应用,对有序加权平均算子的加权向量进行更加科学的确定。此外还可以通过网络爬虫等技术,进行数据挖掘,对于高铁机票等信息进行更为具体的挖掘,通过数据库等技术,可以改进成为实时旅游路线规划模型。
6.3 模型推广
本模型可以通过应用和修正,运用到多种行程问题的科学规划中,其中也包括从事数学和计算机研究的专家学者,在涉及自身旅游路线规划中学以致用,尝试理论与实践的结合,可以为旅行社和旅游相关部门决策提供一定参考。
此外,本模型根据其特性也可以应用到对于某地区某产品的推广,或者某计划覆盖人群的应用当中去。
