CFRP钻削温度场的数值仿真与分析
2021-05-15陈檐成李鹏南王春浩邱新义李树健
陈檐成 李鹏南 王春浩 邱新义 李树健
(湖南科技大学机电工程学院,湘潭 411201)
文 摘 为研究碳纤维增强树脂基复合材料(CFRP)钻削过程传热规律及温度分布特性,在对材料热物理特性均匀化处理的基础上,利用COMSOL Multiphysics 建立单向CFRP 钻削温度场数值仿真模型,探究钻削过程中热量传递及温度场分布规律。结果表明,出口处温度场呈椭圆形分布状态,椭圆形最小值离心率e 为0.771,且椭圆的长轴和纤维方向平行。通过实验对比,纤维方向和垂直纤维方向的温度误差分别为7.5%和7.8%,实验结果验证了数值仿真模型的正确性。
0 引言
碳纤维增强树脂基复合材料(CFRP)具有比模量大、比强度高、耐腐蚀、韧性大和质量轻等诸多优点,在航空航天、风电、汽车、体育、军事等诸多领域广泛应用。由于CFRP 具有各向异性、层间强度低、热导率低等特性,导致其在钻削过程中易形成热积聚和较高温度梯度,产生材料热损伤,进一步诱发分层、毛刺等加工缺陷产生[1-2];由于碳纤维和环氧树脂的热导率和线胀系数存在较大差别,在钻削过程中产生切削热形成的温度场有很高的温度梯度和热应力。尤其当切削表面温度超过环氧树脂的温度(约180℃)时,CFRP 的力学性能和加工表面质量急剧下降[3]。因此温度对CFRP 零部件的加工质量以及刀具耐用度有重要的影响作用[4]。
目前,国内外对CFRP 钻削热和温度的研究相对较少,20世纪开始,DAWSON[5]就致力于切削热和切削温度的研究。LOEWEN[6]和AGAPIOU[7]等基于摩擦系数理论分析对刀具切削温度和热量的产生进行了研究,并且预测钻孔过程中的热现象。到20世纪末21世纪初,CHENG[8]和VOISEY[9]等分别建立在激光钻孔碳纤维材料二维温度场和三维温度场模型来研究复合材料下孔的形状和尺寸及碳纤维热膨胀机制。BONO[10]等通过建立温度场模型对半封闭干式条件的钻削热和温度进行了预测和分析,并且考虑钻削深度和热影响引起的孔径变化,得出孔径变化随孔径深度的增大而增大。近年来,国内学者鲍永杰[11-12]和朱国平[13]等利用有限差分方法分别研究了金刚石磨料刀具用“以磨代钻”制孔、芳纶复合材料的温度场特点和麻花钻钻削单向叠层C/E 的温度场数学值模型,并且通过实验对温度场进行了有效的验证。郝微[14]等利用Abaqus仿真软件建立了芳纶纤维的有限元温度场模型,通过用户子程序对热源进行了编写,来模拟仿真过程中的移动热源。SORRENTIONO[15]等人开发了一种用于钻削过程的温度监测系统。这些工作丰富了CFRP 钻削热方面的研究和温度的测量工作。但由于刀刃处于半封闭空间状态及CFRP 的热物理参数各向异性,导致CFRP 钻孔时形成不规则且复杂的温度场和热量分布,对于钻削单向CFRP 时内部热量传导过程、温度场形成规律等方面研究甚少,对各向异性材料传热机理也需要进一步的研究。
为深入了解单向CFRP 钻削过程传热规律及温度分布特性和解决钻孔温度测量困难等问题。本文针对单向CFRP 材料各向异性、成分分布不均等特点,对树脂和纤维材料热物理特性进行均匀化假设,利用多物理场仿真软件COMSOL Multiphysics建立钻削过程有限元数值模型,研究钻削过程中所产生热量及温度场规律,并通过实验对温度场模型进行验证。
1 单向CFRP钻削温度场数值模型建立
1.1 热物理参数均匀化
由于纤维镶嵌在环氧树脂中且纤维在平行方向和垂直方向的物理特性差异很大。因此在由纤维和树脂组成的单向CFRP 材料,在不同方向的力学性能和热物理性能呈现出很大不同,导致钻削加工过程中内部的力以及热量传递十分复杂。针对二者之间热物理特性的差异以及镶嵌结构的特点,为简化模型本文进行如下合理假设:
(1)在非稳态温度场中树脂和纤维热导率保持恒定;
(2)碳纤维与树脂基体紧密接触,其接触阻抗忽略不计;
(3)碳纤维和树脂均匀排列,纤维均匀嵌入树脂且材料内部不存在制造缺陷。
根据混合法则及学者之前研究经验,综合考虑单向CFRP 中纤维和树脂镶嵌结构影响,将单向CFRP 看作横观各向同性材料并对其进行了均匀化处理的方法[16]如下:

式中,Vc为碳纤维体积分数;ρ为密度,c为热容、k为热导率;下标c、r分别碳纤维和树脂;下标h、l表示平行于纤维和垂直于纤维方向。
1.2 热源模型
根据麻花钻加工特点:主切削刃及横刃承担主要切削作用而副切削刃主要负责导向作用,导致热量集中分布于主切削刃和横刃上。相比而言由麻花钻的副切削刃和孔壁摩擦形成的小量热量可以忽略不计。由于温度场四周受钻削热源的影响较小,温度值趋近于环境温度,所以四周侧面为绝热边界,上下表面与空气直接接触形成对自然对流换热边界条件,整个模型的边界条件设置如图1(a)所示。
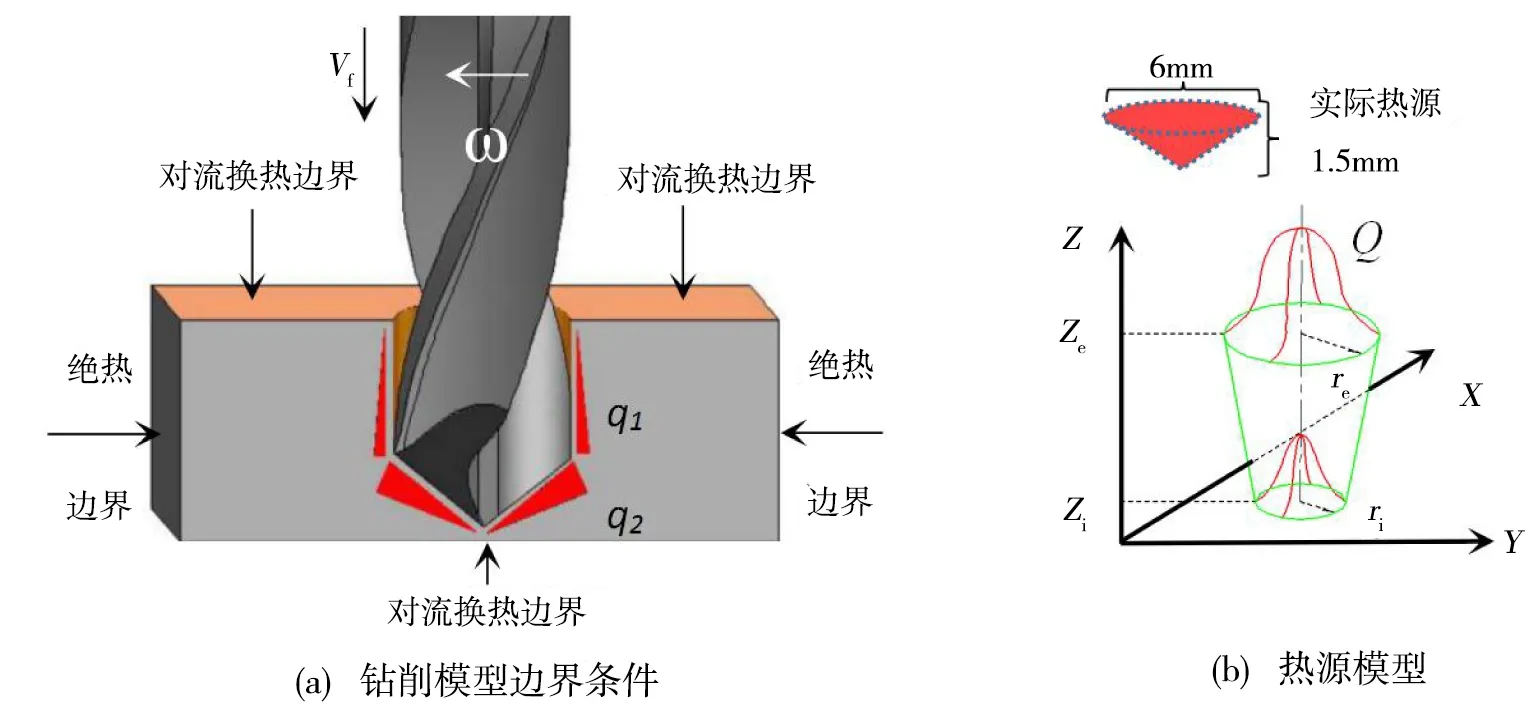
图1 钻削模型边界条件及热源模型Fig.1 Boundary conditions of drilling model and heat source model
如图1所示,根据麻花钻制孔特点,在刀具半径方向热量呈高斯衰减的分布规律,在忽略热量q1后,由横刃和主切削刃产生热源q2简化为圆锥体高斯热源模型,热源模型根据刀具的形状具体尺寸大小。制孔时热能是钻削过程的能量的主要转化形式,假设制孔时总耗能为P;传入CFRP 能量为Q0;能量比例为η;传CFRP中的高斯体热流密度为Qv,则高斯体热流密度计算过程如下:

式中,rc是关于z的热分配系数;re和ri是最大和最小半径;ze和zi是热源z向最大最小值。F是制孔轴向力;v是进给速度;M是扭矩;ω是角速度。由热源简化后实际尺寸:re=3 mm、ri=0 mm、hl=ze-zi=1.5 mm,如图1(b)。
利用COMSOL Multiphysics建立有限元数值仿真模型。钻削几何模型整体尺寸为10 mm×10 mm×5 mm,孔的半径大小为3 mm,网格划分采用自由四边形和扫掠方式进行体单元分割,对孔部位进行网格局部加密。完整网格单元包含26 475 个域单元、6 140 个边界元和438 个边单元,对称边界条件、工件坐标以及纤维方向如图2所示,其他边界条件设置按照图1(a)所示。
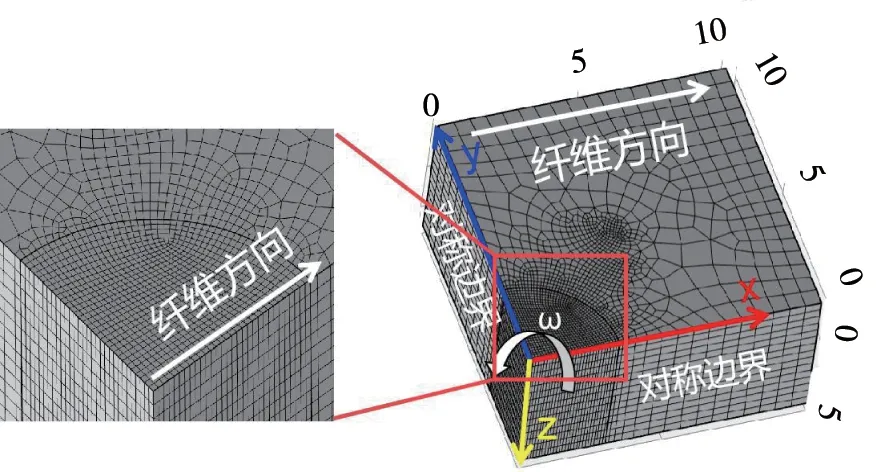
图2 简化模型的边界条件设定及网格划分Fig.2 Boundary condition setting and mesh generation of simplified model
2 热源加载条件
为了获得数值模型中热源加载参数,通过进行钻削实验获取钻削过程的轴向力和扭矩,实验过程如下。
2.1 刀具和材料
实验用的刀具为直径为6 mm 的硬质合金麻花钻,如图1(b)主切削刃在主轴上的投影为1.5 mm,顶角为120°。实验用的材料为单向CFRP,型号为T700,纤维体积分数为(60±5)%,厚度为5 mm,材料的热物理参数如下:kh为4.6 W/(m·K),kl为0.42 W/(m·K),密度为1 496 kg/m3,比热容477.9 J/(kg·K)。
2.2 实验系统及过程
通过图3所示测力系统和测温系统对轴向力和温度进行采集,轴向力用Kistler-9253B 三向压电式测力仪进行采集;同时用快速响应热电偶对孔壁温度进行测量,热电偶位置如图3所示,在试件热电偶的分布位置钻Φ1 的盲孔,预埋孔的位置距离大孔0.2 mm,埋入深度距离加工下表面1 mm。
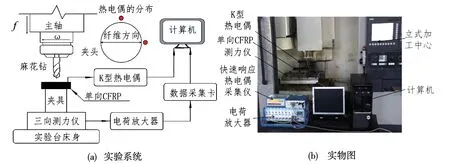
图3 实验系统图与实物图照片Fig.3 Schematic diagram and physical photos of the experimental system
考虑到孔质量缺陷集中在出入口侧,选取了钻削过程中典型位置进行详细分析,钻尖以20 mm/min的速度下移的位置及时间如图4所示。其中0 位置:横刃到达工件出口区域;位置1:主切削刃完全进入工件上表面;位置2 位置;主切削刃刚接触工件下表面;位置3:横刃已经离开了工件下表面,但是主切削刃还没有完全离开下表面;位置4:主切削刃完全钻出工件下表面。
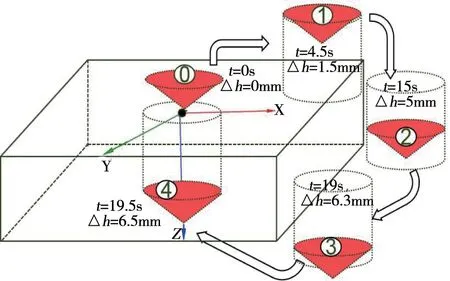
图4 钻削运动过程的典型位置Fig.4 Typical position of drilling process
2.3 热源加载参数
用硬质合金麻花钻对CFRP 进行干式制孔,主轴转速3 000r/min、进给速度20 mm/min 的参数获得轴向力和扭矩如图5所示,可以得出,轴向力在段稳定时间(10~20 s)钻削平均值为107 N,扭矩为3.2 N·m。对流换热系数取20 W/(m2·K)[17],能量比例系数为17%[14],数值仿真模型用到其他参数如表1所示。

图5 钻削过程的轴向力和扭矩Fig.5 Force and torque during drilling

表1 热源加载参数Tab.1 Loading parameters of heat source
3 结果与讨论
3.1 仿真结果及温度分布规律
如图6所示箭头大小和方向表示热量大小和流向,颜色深浅表示温度值大小。从仿真结果可以看出,由于树脂的热导率低以及半封闭式的加工特点,使得大量的热量集中在孔内难以传导出去,在上表面自然对流的环境下热量散失较小,在孔以外的材料沿着纤维方向传递的热量大于垂直纤维方向的热量。当t=4.5 s主切削刃完全进入到CFRP,中心温度最高为126℃。在t=15 s 热源刚接触到底部,由于CFRP 的下表面是与空气形成的对流换热边界,在轴向方向的热量集中在下表面并且出现热量向上移动。随着热源慢慢离开CFRP的下表面,在t=19 s至t=19.5 s 整体的温度出现下降且热量集中在下表面处,从热量传导过程来看主要热量出现往上移动。由于CFRP 平行于纤维方向的热导率大于垂直纤维方向热导率使得平行纤维方向热量明显多于垂直纤维方向的热量。
如图7表示出入口平面平行于纤维和垂直于纤维对应的两个平面的五个位置点时间—温度曲线图。温度随时间变化整体趋势是先上升后下降,钻削过程早期阶段是先缓慢上升,达到最大值后再慢慢下降。

图6 钻孔单向CFRP温度场和热量分布Fig.6 Temperature field and heat distribution of drilling CFRP
位置点1 和位置点2 温升变化趋势相同,在4.5 s前,温度急剧上升,4.5 s 之后上升缓慢,直到钻孔快结束时温度略微下降。但位置点1 的温度始终略高于位置点2的温度,且在4.5 s温度差值达到最大值。位置1 的温度要高于位置2 温度主要原因:由于CFRP 各向异性,0°方向热导率大于90°方向热导率,所以在孔壁上0°方向的温度比沿孔壁90°方向的温度要高。由图7可发现,在约t=4.5 s 后,两点的温度相差最大,最大差值约为15℃。此时钻头主切削刃完全进入CFRP 中,此刻产生最大热量的区域离这两个点最近,所以导致温度差值最大。
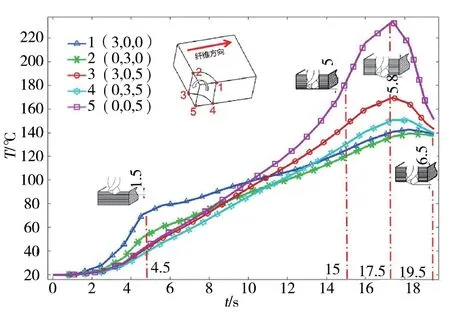
图7 CFRP空间位置温升仿真结果Fig.7 Simulation results of temperature rise in CFRP space position
位置3、4、5 总的温升变化趋势是相同的:0~15 s阶段缓慢上升,15~17.5 s 阶段上升比较快,t=17.5 s温度上升到最大值。相比于位置点1 和2,位置点3和4 温升曲线相同点:沿着纤维方向的位置3 的温度要高于垂直纤维方向的位置4的温度,整体温度是先缓慢上升,直到钻头快接近工件下表面,温度才急剧上升。不同点:温度上升曲率最大值时间点不同,位置点1 和2 在t=4 s 左右而位置点3 和4 在t=16 s 左右。整个钻削加工过程中,CFRP 温度在位置5(下表面的孔圆心上)t=17.5 s时温度达到最大值为230℃。前期温度上升慢的主要原因:热源离测温点的距离较远,热量不断的积累往下移动,垂直纤维方向热导率小热量传递慢,导致热量累积,使得温度升高。后期温度下降是因为钻削过程中产生的热量小于散热的热量,导致温度缓慢下降。由于钻削过程是半封闭的干式加工特点,使得热量集中在刀尖部分,所以中心温度最高。
如图8表示CFRP 出口侧表面温度在不同时刻的温度分布图,以及平行纤维方向和垂直纤维方向温度的变化趋势。温度场宏观体现呈椭圆形,在平行纤维方向和垂直于纤维方向直线上呈现高斯分布,且平行纤维的标准差要大于垂直纤维的标准差。由于不同纤维方向热导率不同,表面温度呈椭圆形分布,并且椭圆长轴平行纤维方向。
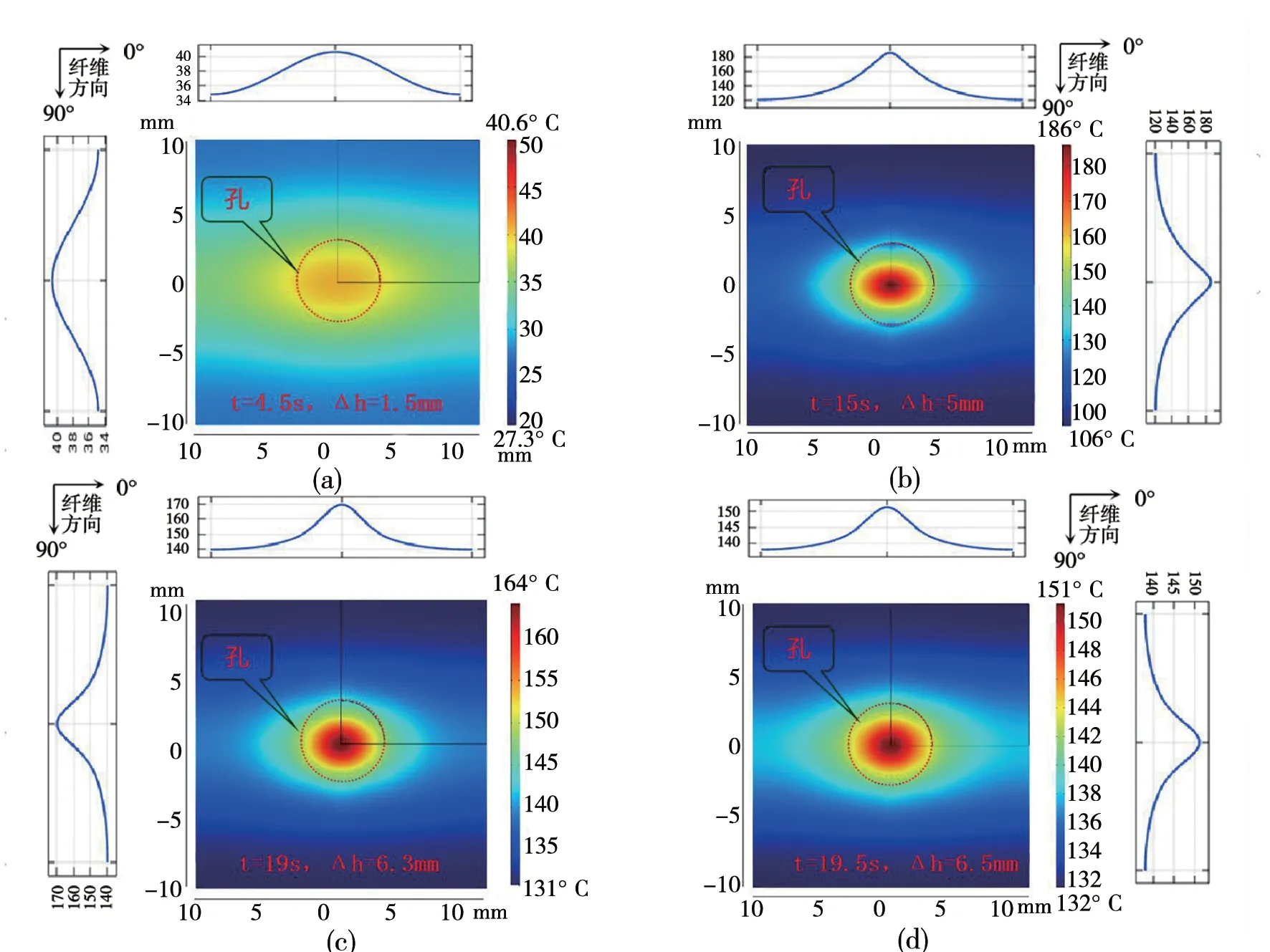
图8 单向CFRP不同时刻出口平面温度分布Fig.8 Temperature distribution in the exit plane of unidirectional CFRP at different moments
如图8(a),钻孔深度为1.5 mm 时,在孔的中心出现最高温度为40.6℃。此时热量来源于横刃挤压和主切削刃切断纤维时的热量,所以此刻下表面出口温度不高。刀具与材料间的短时间、小面积接触导致轴向力和扭矩不足,热量产生较小,并且从上表面传递到下表面的热量更少。当麻花钻完全进入CFRP 工件中并且下降5 mm 时,当钻头横刃刚接触到下表面,此时最高温度为186℃[图8(b)]。由于钻削过程是半封闭状态,随着钻头下移热量不断产生并积累,在钻孔到底部时热量产生和积累最大,所以此刻温度最高。因此图8(b)和(a)相比温度明显升高。
当钻头慢慢往下移,图8(c)是主切削刃还没有完全的离开CFRP 时,此时中心位置的温度为164℃,和图8(b)最高温度相比温度略低。当钻头继续下移,图8(d)表示主切削刃完全离开CFRP下表面出口平面温度分布,最高的预测温度为151℃,温度继续降低。随着切削作用越来越弱,热量随之减少,使得产生的热量小于散失热量,导致温度下降。
为了对温度出口侧椭圆分布进行量化分析,选择出口平面温度等温线来描述,以孔径为椭圆短半径处温度作等温线得到椭圆并计算离心率。椭圆离心率随钻削位置变化规律见图9。CFRP 出口侧温度分布椭圆离心率从位置1 到位置4 先减少后上升,3位置达到最小值离心率e为0.771。从位置1 到位置3热源中心不断的下降,逐渐靠近出口侧。椭圆离心率越来小主要原因:垂直于纤方向的热导率很低,在纤维方向导热快,热量先垂直向下传递,距离越远不同方向的热量就相差越大,导致温度分布椭圆离心率越大。而3位置中心热源离下表面距离越小,所以离心率也就越小。
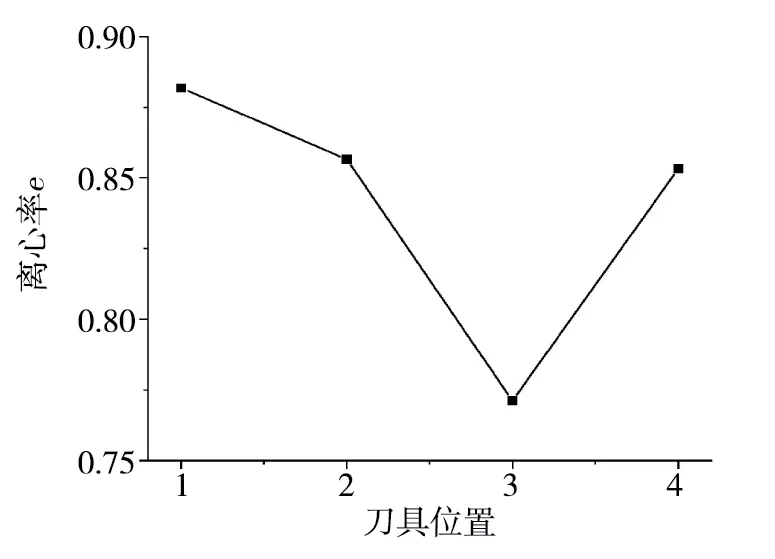
图9 不同位置温度分布椭圆离心率Fig.9 Elliptical eccentricity of temperature distribution at different locations
3.2 模型验证
用图3所示实验平台和表1中加工参数进行钻孔实验获取温度数据,把实验温度曲线与数值仿真温度曲线进行对比。图10显示了不同点温度实验和仿真结果在出口侧温度随时间的变化趋势。随着钻头向下移动切削热量不断积累,温度从室温逐渐升高之后又慢慢的下降。从两者温度变化趋势可以看出,实验和仿真结果变化趋势一致,模型具有良好可信性。
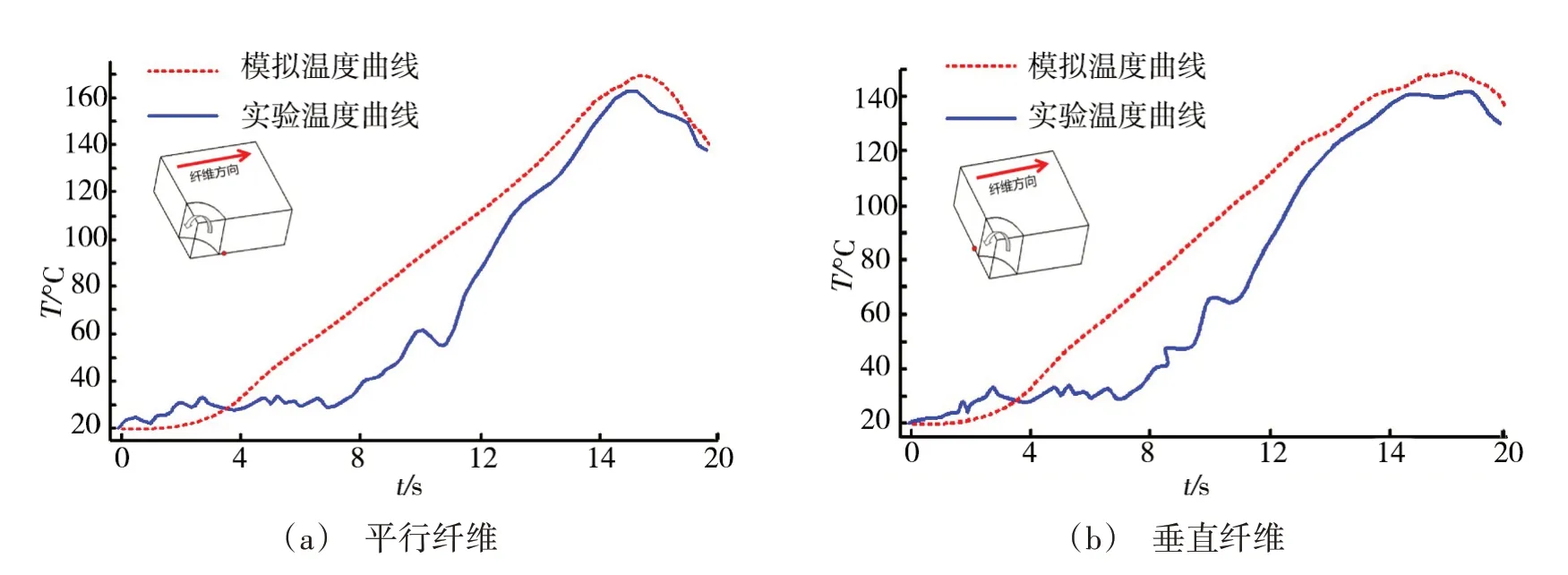
图10 实验和仿真的温升曲线Fig.10 Temperature rise curve of experiment and simulation
从图10可以看出:在4~12 s 时实验值和仿真值相差较大,但是两者温度最大值出现的大小和时间接近。主要原因:在建模时对单向CFRP 热物理参数进行合理均匀化假设,热源简化成稳定热源;实际钻削过程中刀具不断向下进给,每一时刻都有切削热量传导到工件材料上导致温度上升,并且实际钻削过程是一个半封闭空间环境,使得主要热量在刀具和被加工材料接触面上断累积。所以导致仿真温升结果是一个均匀的上升的过程,而实际加工过程的温度前期温度上升很慢。在钻头快接近下表面时曲线上升斜率最大,导致此时间段实验结果与仿真结果相差较大。但是在仿真过程中平行纤维方向温度最大值为171℃,实验值测量最高温度为159℃;垂直纤维方向温度最值为152℃,实验值测量最高温度为141℃;如表2统计两个点实验值和仿真值得相对误差为7.5%,7.8%。并且和文献[14]中的实验现象有相似的变化规律。综上所述:经试验验证表明温度模型和实验结果具有较高的吻合度,具有较高的可信度。
4 结论
(1)在对单向CFRP 材料热物理特性均匀化处理的基础上,利用COMSOL Multiphysics 软件建立单向CFRP 钻削有限元数值仿真模型,获得钻削过程三维温度场。
(2)在仿真结果分析中大量热量集中孔内,孔外沿着纤维方向传递的热量大于垂直纤维方向的热量;出口平面温度分布形状和热源的距离有关,热源中心离平面越远,温度分布的椭圆离心率就越明显且3位置达到最小值e为0.771。
(3)温升曲线和温度场分布有明显的方向性,沿着纤维方向的温度要大于垂直纤维方向的温度值,材料横截面平面内温度场呈椭圆形状且椭圆长轴和纤维方向平行。
(4)利用COMSOL Multiphysics 仿真出口处温度变化和实验数据对比结果在纤维方向和垂直纤维方向温度最大值的误差值分别为7.5%和7.8%,表明仿真与实验结果具有有较好吻合性。
