结合混合核特征映射的空域图像隐写分析
2021-05-14邓利芳党建武王阳萍
邓利芳,党建武,2,3,王阳萍,2,3,王 松,2,3
1.兰州交通大学 电子与信息工程学院,兰州730070
2.甘肃省人工智能与图形图像处理工程研究中心,兰州730070
3.兰州交通大学 计算机科学与技术国家级实验教学示范中心,兰州730070
图像隐写术[1-2]是一种重要的隐蔽通信技术,它利用像素值或者DCT系数的微小变化隐藏图像中的秘密信息。作为隐写术的对抗技术,隐写分析通常认为是一个二分类问题,主要是通过对载体图像提取的相关特征进行分析来判断是否存在隐藏信息[3]。近年来,许多隐写分析特性都取得了良好的性能。隐写分析技术的研究进展有利于检测隐写术的安全性;同时有助于阻止机密信息泄露、遏制病毒和恶意代码等有害信息的传播、打击违法犯罪等活动,具有重要的理论意义和现实意义。
通用隐写分析[4-5]是隐写分析技术的研究热点,通常包括特征提取和监督学习两个阶段[6]。Pevny 等人[7]将图像噪声成分建模为马尔可夫链,以样本概率转移矩阵作为隐写分析特征SPAM(Subtractive Pixel Adjacency Model),在不同载体上实现了稳定的性能。Fridrich 等人[8]以SPAM 模型为基础,提出了使用各种高通滤波器对图像滤波得到丰富的残差模型,提取共生矩阵作为空域富模型特征SRM(Spatial Rich Model),提升了检测性能。Holub等人[9]使用随机高通滤波器对残差图像再滤波,提出基于SRM 随机投影的隐写分析方法PSRM(Projection Spatial Rich Model),在多种自适应隐写算法的检测上优于SRM方法,但计算复杂度太高。Denemark等人[10]提出一种结合信道选择策略的隐写分析方法maxSRM,特征维度与SRM相同,性能比SRM有显著改善。Denemark 等人[11]提出了将残差的期望值累积到富模型的选择信道感知版本中,与对应的spam 子模型特征spamPSRM相比有明显改进。在分类器方面,早期的低维特征使用SVM(Support Vector Machine)分类器[12]。随着特征维度的不断提高,Fridrich 等人提出了专用于隐写分析的基于Fisher 线性判别的FLD 集成分类器[13-14],适合于高维特征空间的快速分类,成功克服了SVM在高维空间中的维数灾难问题。
Boroumand 等人[15]使用机器学习对富模型特征进行Nyström 近似映射,并与FLD 集成分类器结合,提高了2%~3%的空间域内容自适应隐写检测精度。随着隐写分析特征维度增加,特征映射的复杂度增加,当特征维数达到几万维时,远远超过要映射的图像数量,文献[15]提出的映射算法不能直接应用于数万维富模型类型特征。此外,内核选择是提高Nyström 近似映射后分类性能的关键,文献[15]提出的基于单核函数的Nyström 近似映射算法,但是由于单个内核函数的格式和变化空间比较单一,使得鲁棒性和范化能力局限[16]。当样本特征含有未归一化的多维数据,或样本特征数据具有非平面分布的高维特征空间时,单个核函数的性能并不理想[17-18]。
因此,本文基于以上两点不足提出改进。第一,对高维富模型特征先分割,分割后的每组特征分别投影,然后将投影后的特征拼接,最后分类器分类,以解决数万维高维特征不能投影的问题。第二,提出了一种新的混合核函数构造核矩阵,改进特征Nyström近似映射算法,非线性混合核考虑基本核函数的几何形式,该混合核函数简单,计算量比较小,可以有效提高FLD集成分类器的性能。实验结果表明,该方法进一步提高了隐写图像的检测性能。
1 隐写分析流程及特征提取
1.1 提出的隐写分析框架及原理
图像通用隐写分析主要分为两个阶段,设计并提取图像隐写分析特征,分类器训练和分类。图像隐写分析流程如图1所示。
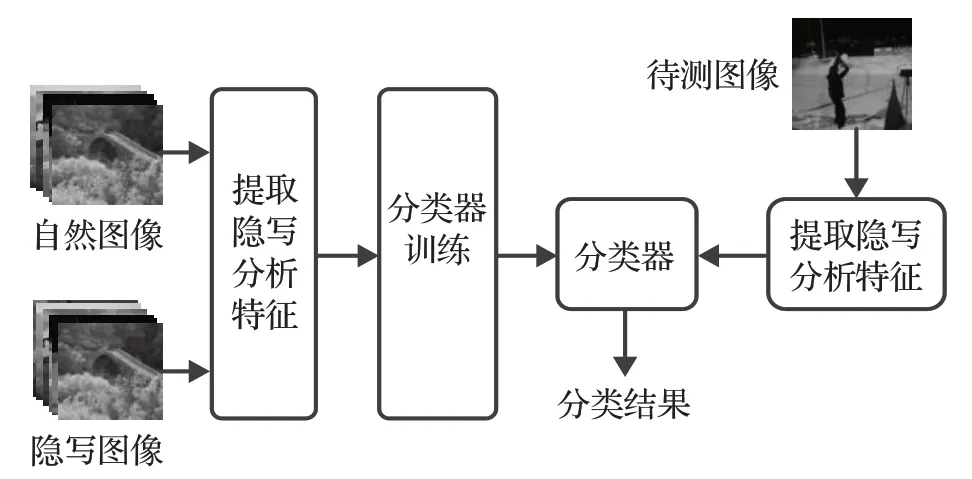
图1 隐写分析过程
1.2 提取隐写分析特征
Fridrich 和Kodovsky 等人提出的SRM 特征提取方法[8]中,设计了丰富的空域高通滤波器,通过使用45 种不同类型的线性和非线性的高通滤波模板来提取噪声残差集。假设一张n1×n2的灰度自然图像和对应的隐写图像分别用X、Y表示,X=(Xij)∈{0,1,…,255}n1×n2,Xij表示自然图像的像素,残差R=(Rij)用式(1)计算:

其中,c为残差阶数,Nij是局部邻域像素,X^ij(·)是定义在Nij上cXij的预测像素。
然后用式(2)对每个残差图像量化和截断,阈值T=2,量化因子q∈{1,1.5,2}。并计算残差图像的四维共现矩阵C(SRM),SRM由四个相邻的量化噪声残差样本构成的多个共现矩阵组成,例如水平方向的共现用式(3)计算:

再经过对称合并规则,将所有元素重新排成特征向量,即为34 671维的SRM特征。
maxSRM 的构建方式与SRM 相同,但对共现矩阵的形成过程进行了修改,以考虑图像中估计的嵌入变化概率在maxSRM中,修改定义为式(4):
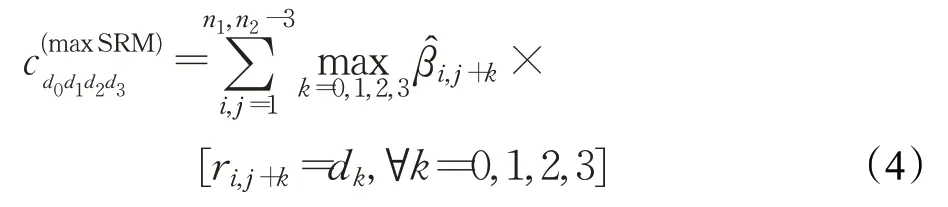
maxSRM将四个残差的嵌入变化概率的最大值相加,组成的像素组的更改概率很小,对共现值的影响较小。
SRM采用水平和垂直扫描,为了进一步提高检测,将所有共现扫描方向都替换为倾斜方向“d2”,称其为maxSRMd2[10],计算共现如式(5),本文采用maxSRMd2作为隐写分析特征。
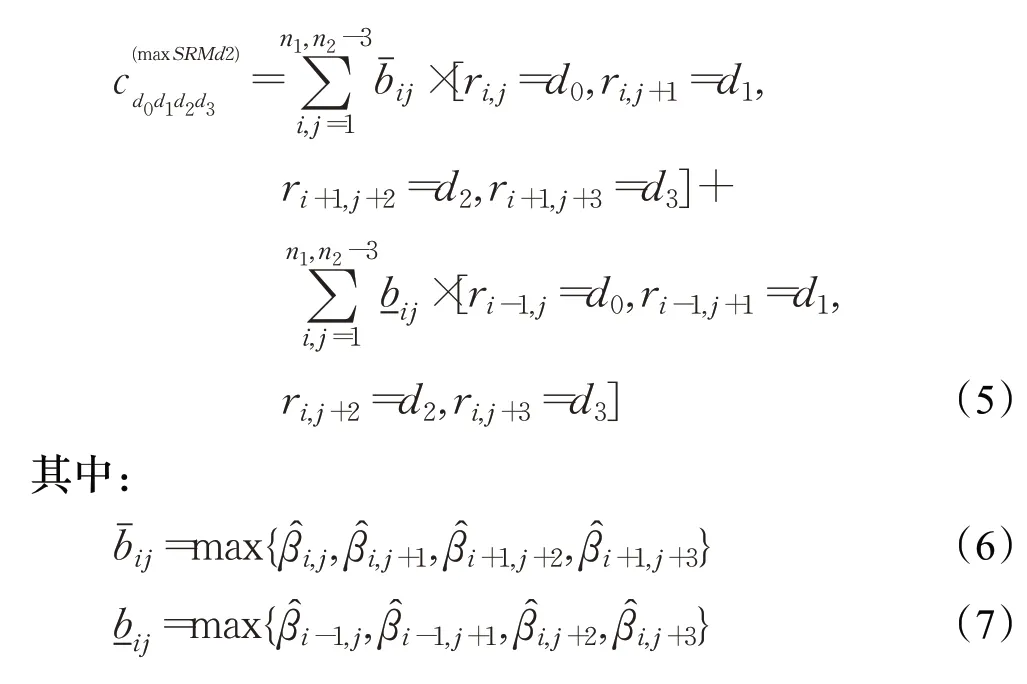
2 结合混合核特征映射的隐写分析
2.1 提出的隐写分析框架
本文提出了一种结合非线性混合核特征映射的图像隐写分析框架,如图2 所示,对提取隐写分析富模型特征先进行分割,分割后每组训练集特征G1,G2,…,Gn用结合非线性混合核的Nyström投影算法映射,再用训练集训练好的模型对待检测图像进行学习变换,然后将投影后的特征F1,F2,…,Fn,进行拼接,最后FLD 集成分类器训练和分类。
2.2 特征分割
用于隐写的图像具有内容丰富、纹理复杂等特性。在特征映射算法中,要求用于训练的图像数量必须大于特征维数,而在采用BOSSbase1.01 图像库进行隐写分析时,提取的高维富模型特征维数超过数万维,非线性特征映射不能直接用于整个富模型特征。因此,提出先特征分割再投影的方法。
为使分割后的映射特征块的数据大小均匀,首先对提取的富模型高维特征采用PGO(Pine Growth Optimization)特征[19]选择算法去除不相关的特征,减少特征维度,稳定数值计算和特征向量问题中的病态矩阵,而且能加快投影速度。然后对剩余的特征分割,对分割后的每组特征进行映射,再拼接映射后的特征,最后用分类器分类。具体步骤如下:
步骤1特征分解,去除不相关的特征得到新的隐写分析特征,自然图像特征和隐写图像特征分别表示为cover和stego。将该特征对纵向分解为若干块G1,G2,…,Gn,即划分为各个子模型,对每个特征块进行映射。提取的图像特征大小为10 000×34 671(即10 000 张图像,提取的特征维度为34 671),去除不相关特征后新的特征大小为10 000×32 016 维,将32 016 维的特征对纵向分解为8个特征块,即用于训练和测试的每个特征块大小为5 000×4 002。
步骤2对每个特征块分别进行映射,以解决特征维数高而导致不能直接进行非线性特征映射的问题,每个特征块分别投影还降低了计算复杂度,改善了特征映射时运行内存高的问题。
步骤3将映射后的每组特征F1,F2,…,Fn按照原来顺序进行拼接,合成图像高维富模型特征,合成后的特征不会损失特征数据的精度,且提升了计算速度,减少了时间开销和硬件成本。经过结合混合核的特征映射增强了数据的可区分性,提升了分类器的性能。
步骤4对映射后的图像高维富模型特征用FLD集成分类器分类并评估结果。
3 结合非线性混合核的特征映射
3.1 核函数
核函数将输入数据隐式映射到高维特征空间,使得数据线性可分或线性可分性增加[16]。在再生核希尔伯特空间RKHS(Reproducing Kernel Hilbert Spaces)中如式(8)所示,特征空间中的内积在输入空间中具有等价的核,k是正定函数,满足Mercer’s 定理[20]。对应的核矩阵K写成式(9):

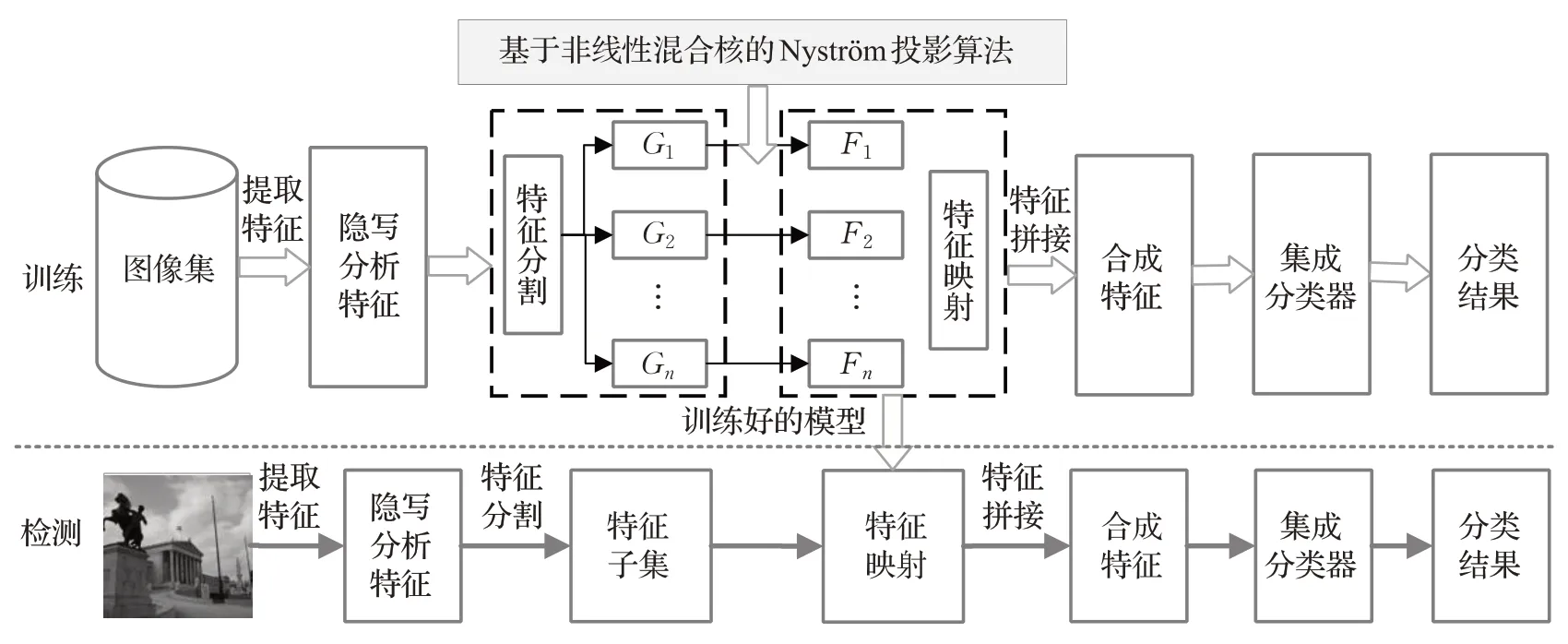
图2 结合非线性混合核特征映射的图像隐写分析流程
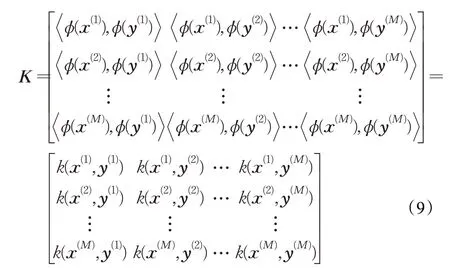
其中,x,y 为特征向量,分别表示自然图像和隐写图像特征向量;φ 为映射函数;M 为图像数量。
核函数的选择严重影响了特征映射后的分类精度。最优核函数不仅能减小分类误差,而且能防止训练数据的过拟合。用于映射的以下核函数都是计算机视觉中的内核,具有可加性和齐次性[21]。
(1)线性核:

线性核函数用于线性可分的数据,具备良好的性能。但不能对线性不可分数据进行分类。 x 和y 用于L2范化,源于Ali-Silvey距离。
(2)Hellinger核

Hellinger核源于Bhattacharyya距离,x 和y 用L1范化。
(3)线性核和Hellinger核的指数形式
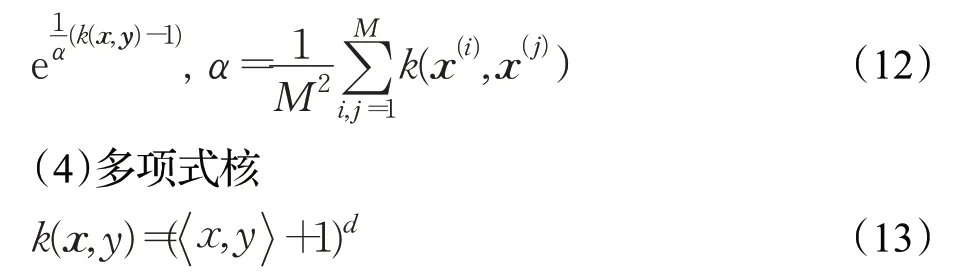
多项式核为全局函数,其映射的数据维数随着d 的增大而增大,可以获得远离待预测数据的全局信息,具有很强的外推能力。
3.2 非线性混合核
在许多情况下单核函数的格式相对固定、变化空间相对狭小,使鲁棒性和泛化能力具有局限性,单核函数并不是映射的理想内核[16-17]。与单内核函数相比,对于含有异构信息、数据规模大、多维特征不规则及在高维空间分布不平坦等现象[22]的样本特征,混合核更具有优势。通过设计的混合核函数,可以有效改善泛化能力和提高鲁棒性,提高FLD集成分类器的性能。使用现有的内核函数可以生成更高效的,并具有每个核函数属性的新混合核函数。
核函数k1(x,y)和k2(x,y)是两个合法核,c 是常数,式(14)也是合法的核[18]。还可以对不同子集使用不用的核。混合核融合了来自不同信息源的信息,其中每个核都根据自己的领域度量相似性。
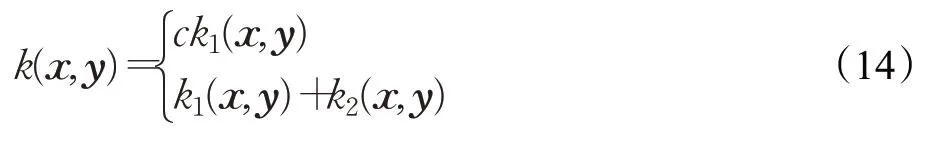
线性混合核函数可以看作是基本核函数的算术平均,以往的研究多集中在线性混合核函数上。本文从非线性混合核的角度出发,考虑基本核函数的几何形式,即用非线性混合核函数投影算法进行特征映射。构造的非线性混合核表达式如式(15)所示,并证明式(15)是合法的核函数。

命题1假设k1和k2是X×X(X ⊆Rn)的核函数,φ是X →RN的映射,证明非线性混合核式(15)是合法的内核。
证明认为S 是一个有限集合{x1,x2,…,xL} ,并假设K1和K2为核函数k1和k2在这些点上对应的核矩阵。考虑对任意向量α ∈R+,满足α′kα ≥0,则K 是半正定的。因为α′k1α ≥0,α′k2α ≥0,所以α′(k1·k2)α ≥0,因此K1·K2是半正定的,且满足Mercer’s定理,故k1·k2是核函数,即式(15)为核函数。
因此,当这两个单核函数都是正定的时,这种类型的混合内核函数是有意义的。平衡投影后的检测性能和时间复杂度,选取Linear核和Hellinger核作为非线性混合核的基本核,构造的新非线性混合核函数的具体表达式如式(16)所示,命名为Multi-kernel。
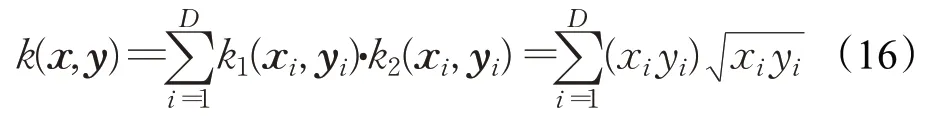
构造的新非线性混合核空间不能简单地看作是每个基本核空间的直积,该混合核函数具有更为复杂的核空间结构。
3.3 映射过程
3.3.1 从核到特征映射
对特征的每组分量x,y,核函数k(x,y)的特征映射φ(x)是将x 映射到一向量空间的内积<·,·>,k(x,y)的齐次特性如式(17)所示:

对于任意齐次核k(x,y)在R 上存在一个对称非负测量密度函数κ(λ)dλ,λ ∈R+,如式(18):

公式(20)无限维特征向量映射的显式形式。λ可以看作特征向量φ(x)的索引,所以特征映射[φ(x)]λ可以在内核的封闭形式计算。
3.3.2 结合混合核的特征Nyström近似映射
找到一个变换任务使得变换后两个向量的点积与对它们核的求值重合,具体表述为:给定的训练映射的图像数量M大于特征维数D,用自然图像特征向量来训练映射φ,找到向量φ(x()i)∈RM,φ为映射函数,即对i,j∈{1,2,…,M},变换任务如式(21)所示:
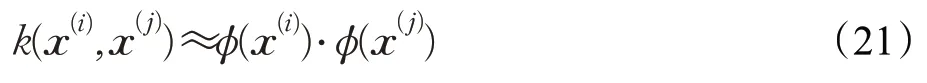
然后转化优化问题求解:
步骤1用φa(x) 表示φ(x)∈RM的第a个分量,1 ≤a≤M,为使式(21)两者的差最小,转化为式(22):
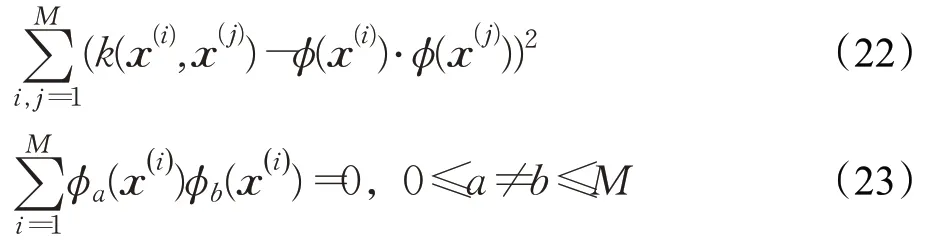
式(23)为约束条件,即使得M维特征空间的描述符是非冗余的,本质要求转换后的特征向量是不相关的。

在构建映射φ的过程中,为得到性能最优的结果,规定特征映射前后保留特征维数不变。提出的混合核使用L1范化,结合非线性混合核映射后的向量φ(z)如式(27)所示:
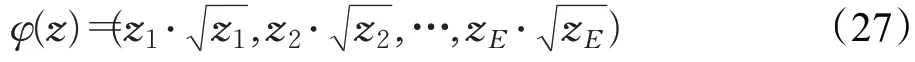
由于特征转换只依赖于少量的自然图像特征,而不依赖于具体的隐写算法或嵌入的有效负荷大小,所以形成核矩阵、计算核矩阵的特征值和特征向量只需要在训练集中计算一次,这在很大程度上减少了映射时间。映射采用简单内核的封闭形式,与分类器训练相比,特征投影的时间复杂度要低得多。
4 实验及分析
4.1 实验基础
为了验证本文方法的有效性,实验使用BOSSbase1.01图像库,其中包含10 000幅大小为512×512,8位的灰度图像,包括人物、风景、建筑等,图库示例如图3 所示。实验以10 000张图像作为隐写的载体,分别采用三种主流隐写方案S_UNIWARD[23]、WOW[24]、MVG[25]生成隐写图像。然后分别提取载体图像和隐写图像的特征,映射特征并分类。算法运行硬件环境为Windows10,Intel®Core™i7-8700 CPU @3.20 GHz 3.19 GHz,运行内存16 GB。

图3 BOSSbase1.01图像库示例
将载体图像和对应的隐写图像对随机选取一半为训练样本,另一半为测试样本。提取的特征维度均为34 671维。去除不具有影响力的特征后,特征维数降为32 016 维。实验中将5 000×32 016 维特征分解为8 个特征块。每个特征块大小为5 000×4 002,满足训练特征的图像数量大于特征维数。然后对每个特征块进行投影,再将投影后的特征拼接成新的特征。为测试算法的检测性能,用FLD集成分类器进行检测[13-14]实验采用FLD分类器2.0版本。
在图像隐写分析领域常用最小总检测错误率衡量隐写分析的性能。最小总检测错误率通常包括两方面:虚警率和漏检率。计算公式如式(28):
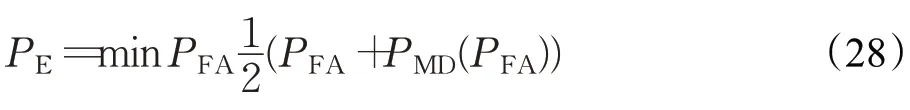
其中,PE为最小总检测错误率,PFA为虚警率,PMD为漏检率。每组实验重复两次取平均值,以保证实验数据的可靠性。
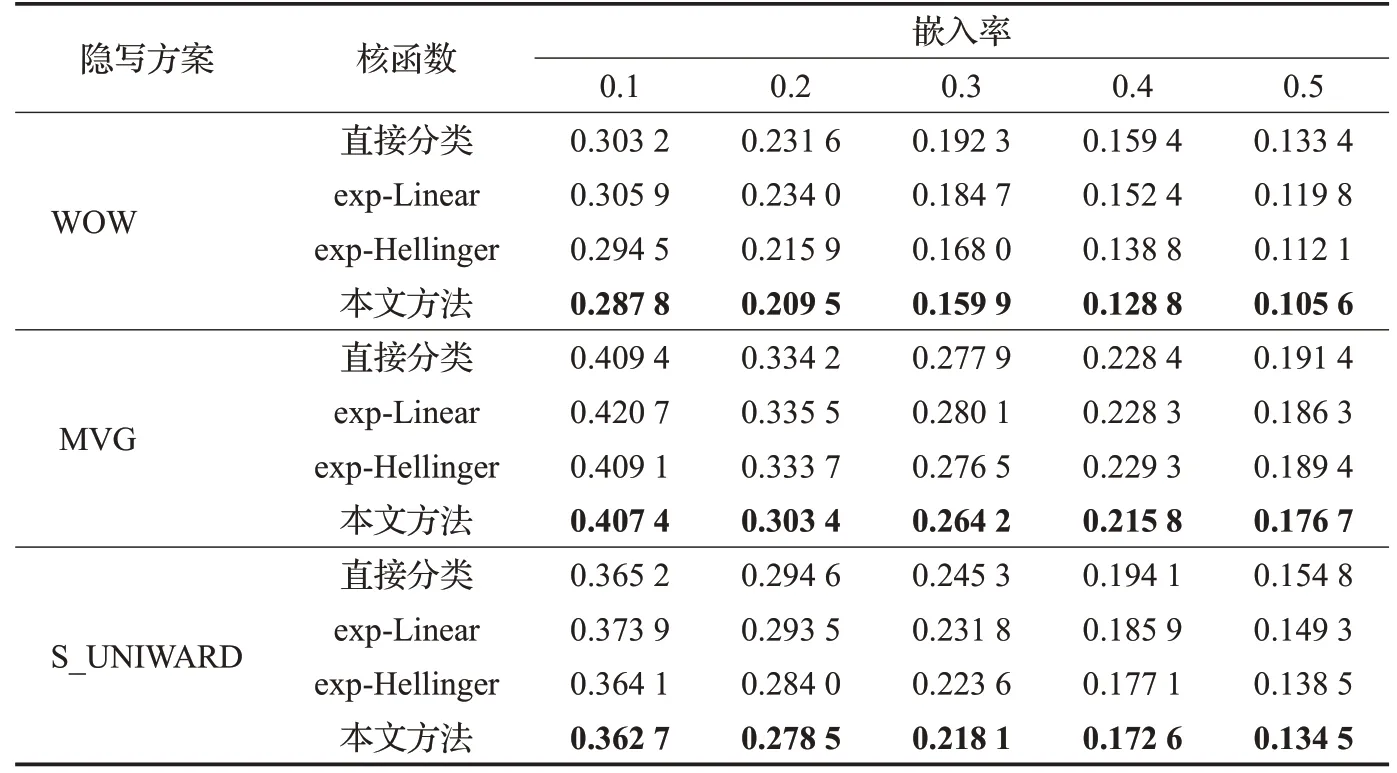
表1 三种隐写方案在不同嵌入率下的检测错误率
4.2 实验结果和分析
为验证本文提出方法的有效性,选取三种主流的隐写方案,研究提取的富模型特征使用非线性特征映射的优势,并且评估本文提出的非线性混合核函数的有效性,能进一步增强数据的可分性,降低分类器分类的错误率。实验分别采用文献[13]中的FLD 集成分类器对提取的隐写分析特征直接分类,文献[15]用结合单核的映射算法投影后再用FLD分类器分类,与本文结合非线性混合核特征投影算法投影后分类的实验作对比,其实验结果如表1所示。
在实验中,使用了五种不同的有效负荷大小即嵌入率,包括0.1、0.2、0.3、0.4 和0.5,在隐写分析方案中实现的最低的PE(在特定负载下)以粗体突出显示。从表1中发现,三种隐写方案对应的富模型特征经过投影后再分类的效果都要比直接分类的效果好,对于WOW隐写的图像进行隐写分析,负载为0.3、0.4、0.5时,特征投影后分类比文献[13]的分类器直接分类的最小检测误差降低2%,采用结合混合核的投影算法要比文献[15]中单核投影算法的性能要好,负载为0.3 时最小检测错误率降低1%。MVG隐写方案的图像隐写检测中,结合混合核的投影算法与文献[15]中exp-Hellinger核的投影算法相比,有效负载为0.2时,最小检测错误率降低3%,有效负载为0.4时最小分类误差降低1.35%。S_UNIWARD的隐写图像检测结果中,结合混合核投影算法投影后分类结果也要比前面三种的结果有所改进。WVG隐写方案的隐写图像检测性能改进的效果优于其他两种隐写方案。与单核映射算法相比,混合核映射对隐写分析的误差更加明显,原因在于:混合核映射通过富模型特征的多样性,有效增加了自然图像和隐写图像两类特征数据的类间距离,使得数据的可分性增强,提高了泛化能力。
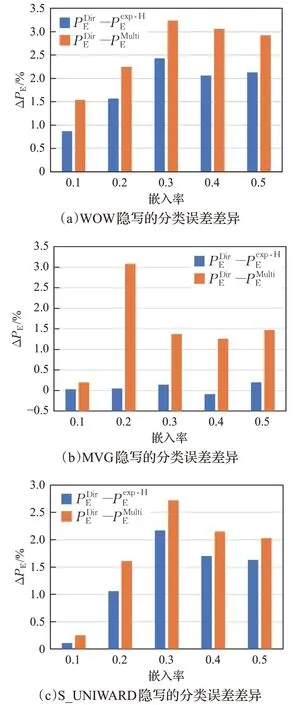
图4 不同嵌入率下,直接分类、exp-Hellinger和Multi-kernel投影后分类的误差变化
为了更好地对比检测的改进,在图4 中,实现了直接分类的最小检测错误率、文献[15]方法和本文方法的最小检测错误率之间的差异,差异以百分比表示。比较结果表明,在所有四种嵌入算法中均获得了一致的检测增强。MVG 获得了最大的提升。
为了比较不同核函数对分类性能的影响。选取五种核函数做实验,其比较结果如图5所示。当嵌入率为0.3 时,三种隐写方案在基于五种核函数的投影算法投影后分类的误差比较可看出,使用本文提出的非线性混合核,检测错误率均优于结合单核的投影后分类的误差。其他几种嵌入率下,也能获得类似结果。
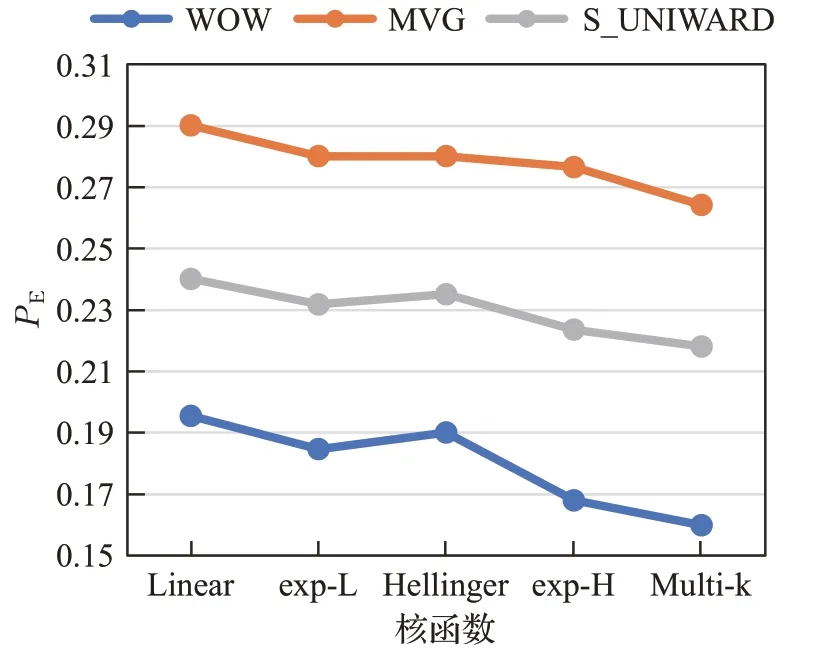
图5 嵌入率为0.3,不同核函数投影算法对特征映射后分类误差的比较
内核函数的选择是影响特征映射后FLD 集成分类器的分类性能的关键,同时核函数的复杂程度直接影响特征映射时间复杂度,由于隐写分析的特征样本数据量大、特征维数高,当选择的核函数较复杂时,会严重增加特征映射时间,在实际中可用性大大降低。所以选取相对简单的四种单核函数,文献[15]用exp-Hellinger核实现了最佳分类性能。表2为exp-Hellinger和提出的混合核函数Multi-kernel 投影时间作比较。由于exp-Hellinger的指数运算增加了投影时间,而构造的非线性混合核函数相对简单,避免了指数运算,所以两者的投影时间相当,这就保证了在不增加映射时间复杂度的情况下进一步降低了检测误差。
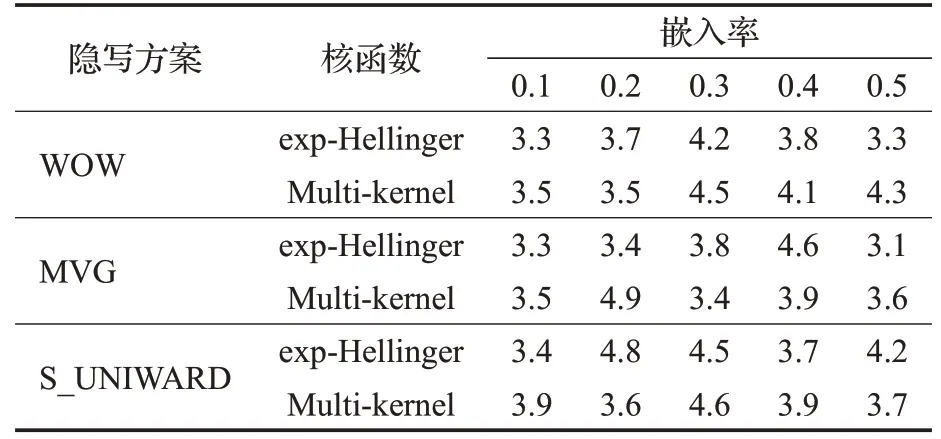
表2 结合exp-Hellinger核和非线性混合核Multi-kernel投影算法的特征投影时间比较h
5 总结和展望
本文提出对高维富模型特征先分割再投影的思想,同时考虑不同核函数投影算法对分类性能的影响,提出了新的非线性混合核函数。该混合核有效克服了单核函数的格式相对固定及映射的特征变换空间相对小的问题。结合非线性混合核的特征映射算法使得两类特征数据的类间距离增加,使数据的可分性增强。实验结果表明,在投影时间相当的情况下,本文方法进一步提升了检测性能。同时对高维特征采用分组投影方法降低了内存需求。未来将进一步研究特征投影算法,缩短投影所需要的时间,并研究更有效的特征提取方案。
