融合KNN优化的密度峰值和FCM聚类算法
2021-05-14兰红,黄敏
兰 红,黄 敏
江西理工大学 信息工程学院,江西 赣州341000
聚类(clustering)就是将一个数据集分成多个簇(cluster)或类,使得在同一类簇中的数据样本点之间具有相对高的相似度,而不同类簇中的数据样本点差别较大。根据聚类的结果可以从数据中发现规律和知识,探索出藏在数据之后的规律和模式。聚类算法被普遍地运用在数据科学分析和实际工程领域中[1-4],经过许多国内外研究人员的努力,产生了许多优秀的聚类算法,根据研究方向和算法实现原理的不同,目前聚类算法可划分为基于密度的方法、基于网格的方法、基于层次的方法、基于模型的方法和基于划分式方法等五种主流方法[5]。
模糊C 均值(Fuzzy C-Means,FCM)算法[6]是基于划分式的聚类算法,此算法的基本思想是引入隶属度概念来量化样本点从属于每个类簇的数值大小,由此进行划分判断,使得划分到同一类簇的样本间相似度最大、不同类簇的样本间相似度最小,已达到对数据集划分为各类簇的目的,在模式识别、数据挖掘、数据分析、矢量量化以及图像分割等领域应用比较广泛[7-8]。FCM算法是C-Means算法的衍生改进算法,C-Means算法对数据集划分属于硬性、具体的划分,但FCM算法对数据集的划分属于软(柔)性、模糊的划分。FCM 算法没有考虑到样本点的邻域关系和局部信息,容易导致算法对噪声敏感。此外,FCM 算法在初始聚类中心的选取原则上是随机选取,若初始聚类中心选择不理想甚至选择了噪声点作为聚类中心,将导致算法收敛于局部极值点或得到错误的聚类结果。面对以上问题,许多科研专家使用不同的方法来改进FCM 算法。文献[9-10]采用改良模糊加权指数的计算方法,聚类效果良好;文献[11-12]通过改变数据加权的策略来优化迭代过程从而提高聚类的效果;文献[13-14]从初始中心点的选择出发,使用各种方法优化初始中心点的选择来避免选中噪声点,提高聚类的准确性;文献[15-16]是根据数据集的空间分布信息,改变目标函数从而得到新的隶属度计算方法;文献[17-18]则是通过把密度峰值算法与FCM算法相结合的方法来优化FCM算法,达到了较好的效果。
文献[9-16]这些改进方法都是根据模糊C均值算法某个方面的不足朝特定的方向优化改良FCM 算法,聚类效果在一定程度上得到了提升和改善,但是未综合考虑到数据样本中的样本数据和噪声数据点的空间分布信息对聚类效果的影响。文献[17-18]主要是利用样本的局部密度信息,使用密度峰值算法来优化初始中心的选择,从而使得改进后的算法在抗噪性和全局收敛能力上超过其他算法,但是在使用密度峰值算法时保留了需要主观选择的截断距离dC,影响了聚类效果,尤其在数据集样本规模较小时影响较大。因此,本文提出了一种融合KNN优化的密度峰值和FCM聚类的改进算法,使用KNN来代替截断距离dC,既解决了需要主观选择截断距离的问题又使得在样本密度度量方面有了统一的密度度量准则,进一步提升了FCM算法的性能。
1 KNN优化的DPC算法
1.1 算法基本思想
快速搜索和查找样本密度峰值的聚类算法[19](clustering by fast search and find of density peaks,DPC算法)可以快速地找到任意形态、规模数据集样本的密度峰值即类簇中心点,在大规模聚类处理分析方面表现出色,其基本思想是,在理想情况下,类簇中心周围的样本点的局部密度要小于类簇中心的局部密度,且不同类簇中心间应有较远的距离。根据这两个特点,设计了两个变量,一个是样本i 的局部密度ρi;另一个是样本i到距离它最近且局部密度比它大的样本i 的距离δi,它们的定义如公式(1)和(2)所示:


由公式(1)~(3)可知,当数据样本点i 的局部密度ρi最大时,它的δi距离将远大于其他样本点的δi距离,δi距离异常大的点往往是该数据样本集的类簇中心,其样本点的局部密度也相对较大,因此,DPC 算法是用构造样本点的局部密度ρi和样本距离δi值二维决策图的方法来选择数据集样本的类簇中心(ρi和δi值都较大时对应的点)。但是当每个类簇数据集规模都较小时,样本的稀疏性会导致类簇中心点模糊,要找到其密度峰值点是十分困难的[19],这时将采用综合变量γi构成的曲线决策图来寻找密度峰值点[19],其公式如式(4)所示:

γi值越大则为密度峰值点的可能性越大,对γi排序再从中选择最大的若干个点作为密度峰值点,其余的样本点分配到与其最近的密度峰值点形成类簇。为了避免样本噪声点的影响,DPC算法给每个类簇定义了边界区域:由属于该类簇但与其他类簇数据样本点的距离小于截断距离dc的数据样本点构成[21]。设置一个阈值ρb:每个类簇边界区域数据样本点总数值[17]。每个类簇中的数据样本点的局部密度大于ρb值则视为核,反之则视为噪声样本点,由此得到最终的聚类结果。
1.2 算法局限性分析
(1)根据数据集样本规模的大小不同,采用了两种不同度量样本局部密度的方法,但是没有一个客观科学的标准来判定数据集规模的大小,导致聚类结果受样本局部密度度量方法的影响。
(2)当数据集相对复杂时,不同类簇的密度会有较大的差异,使用欧氏距离进行密度度量,取不同的截断距离将会导致完全不同的聚类结果,容易出错,并且截断距离是人为设定,没有一个明确的标准和规范。
(3)DPC 聚类算法在样本聚类时具有连错效应,即若有一个样本分类错误,其他样本接着分类错误,将导致千差万别的聚类结果。
2 KDPC和FCM的融合算法
2.1 DPC算法的改进KDPC
本文引入了样本的K 近邻信息来对DPC算法进行改进优化(KDPC),为了统一DPC聚类算法中两种计算样本局部密度的方法准则,提出了一种新的不受dc影响的样本局部密度计算方法,该方法适用于不同规模的数据集。
使用样本点的K 邻近信息来计算样本的局部密度ρi值,其定义如式(5)所示:

当样本点的K 邻近距离越大时,其ρi值就越小,否则反之。与式(1)和式(3)相比较,参与式(5)的计算范围要小很多,原本需要样本点与数据集其他所有样本点之间的距离参与密度计算,现在只要样本点与之相邻的K 个样本点之间的距离参与密度计算即可,更加能够反映出样本点的局部密度信息。
为了减少噪声样本的干扰,在计算数据样本点的局部密度之前,要将噪声样本剔除,为了识别出噪声样本,本文对其有如下定义:若样本点的KNN 距离大于数据集中所有样本点的平均KNN 距离,则该样本点被认定为噪声样本点。样本点的KNN距离Kd(i)计算如式(6)所示,数据集中所有样本点的平均KNN距离M 计算如式(7)所示,噪声样本点的识别函数N 如式(8)所示。
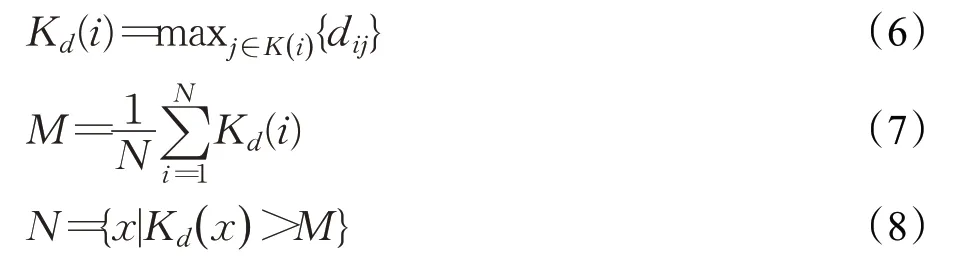
上式中K( i )为数据样本点i 的K 邻近点集合,N 表示数据集中总样本数。
KDPC 算法首先运用式(6)~(8)识别标记噪声样本,减少噪声对整体算法的影响,其次用引入K 邻近信息的式(5)来代替式(1)和(3)计算出数据集中每个样本点的局部密度值,接着用式(2)计算出每个样本点的δi值,最后使用式(4)来选取数据集中的若干密度峰值即聚类中心点。KDPC 算法避免了DPC 算法需要主观判断数据集规模、人工设定截断距离dc等问题,从而更加精准地找到数据集的密度峰值点。
2.2 FCM聚类算法
FCM聚类算法将数据集样本点之间的相似程度定义为隶属度,假设数据集为X={x1,x2,…,xn},被划分为i 类,聚类中心点为ci,则数据集中任意样本点j 与某个类中心点ci的隶属度为uij,其目标函数(9)和约束条件(10)如下所示:

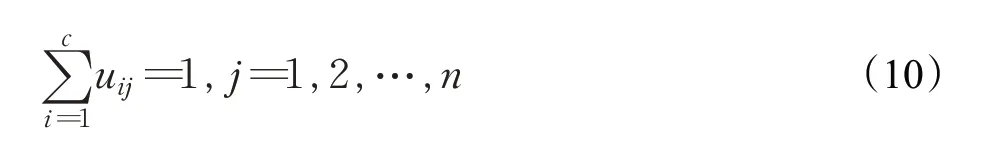
式中,m 为隶属度uij的指数权重因子,n 为数据集样本总数。采用拉格朗日乘数法及其他数学运算方法,当目标函数最小时,解出uij的值为式(11)所示,ci的值为式(12)所示。
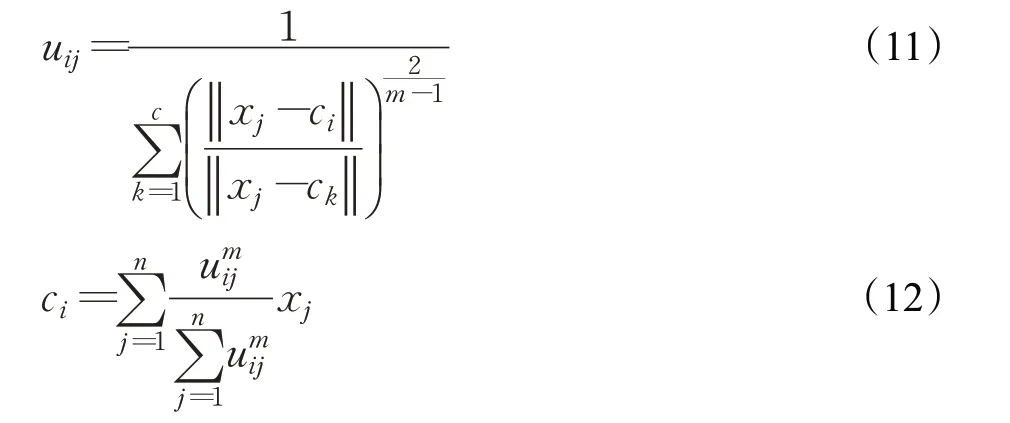
FCM 算法的步骤为:先随机初始化一个满足约束条件(10)的uij值,然后根据式(12)计算出ci的值,其次将得到的ci作为输入,根据式(11)计算出新的uij值,此时根据式(9)计算出目标函数J 值。再次根据式(12)、(11)和(9)迭代计算出ci、uij和J 的值,如此循环迭代计算,当J 达到最小值时停止计算,输出ci和uij的值,完成聚类。
2.3 算法思想
算法总体可分为两部分,(1)KDPC 部分:运用KDPC算法思想计算出数据集中所有样本点的γi值,根据γi值大小进行排序(从大到小排序),假设数据集可分为c 类,则选取γi值排序后的前c 个样本点作为该数据集的聚类中心点;(2)FCM部分:运用第(1)部分获得的聚类中心,计算出对应的隶属度uij,开始循环迭代计算,满足终止条件完成聚类,获得更加精准的聚类结果。
2.4 算法步骤
KDPC-FCM算法步骤如下:
KDPC部分:运用改进的密度峰值算法初始化数据集的聚类中心,具体步骤如算法1所示。
算法1KDPC部分算法步骤
输入:样本数据集X ,类别数c。
输出:初始化聚类中心集ci(0)。
处理过程:
步骤1数据预处理:对数据进行归一化处理。
步骤2根据式(6)~(8)对数据集中的噪声样本进行识别并标记,去除噪声样本点。
步骤3计算数据集中非噪声样本间的欧式距离,根据式(5)计算出非噪声样本点的局部密度ρi值。
步骤4根据步骤3 中获得的ρi值,运用式(2)计算出非噪声样本点的δi值。
步骤5根据式(4)计算出非噪声样本点的γi值,由该值大小将非噪声样本点进行从大到小排序。
步骤6在排序后的非噪声样本点中选取前c 个样本点,得到该数据集的初始化聚类中心集ci(0)。
FCM部分:根据KDPC部分得到的聚类中心集ci(0),使用FCM 算法进行循环迭代计算,获取聚类结果。具体步骤如算法2所示。
算法2FCM部分算法步骤
输入:样本数据集X,初始化聚类中心集ci(0),指数权重因子m(一般选取m=2 效果最佳)。
输出:聚类中心集ci,隶属度矩阵uij。
处理过程:
步骤1初始化迭代次数t,令t=0。
步骤2根据初始化聚类中心集ci(t),由式(11)计算出隶属度矩阵uij(t)。
步骤3根据ci(t)、uij(t),由式(9)计算出目标函数J(t)值。
步骤4根据隶属度矩阵uij(t),由式(12)计算出新的聚类中心集ci(t+1)。
步骤5根据聚类中心集ci(t+1),由式(11)计算出新的隶属度矩阵uij(t+1)。
步骤6根据ci(t+1)、uij(t+1),由式(9)计算出新的目标函数J(t+1)值。
步骤7判断J(t)-J(t+1)>0 是否成立,若是,则t=t+1 并转到步骤4继续执行;否则,终止运算。
步骤8完成上述7 步,多次迭代后得到最终的聚类中心集ci值和隶属度矩阵uij,由此划分数据集,得到聚类结果。
2.5 算法具体流程
KDPC-FCM算法的总体流程如图1所示,首先对数据进行归一化预处理,减少后续运算量,运用自定义的噪声识别函数N将数据集中的噪声样本标记剔除,然后利用式(5)计算出每个非噪声样本点的局部密度ρi,接着使用式(2)和(4)分别计算出非噪声样本点的δi值和γi值,根据γi值的大小排序得到数据集的初始化聚类中心点集合ci(0),到此KDPC 部分结束;开始FCM 部分:初始化指数权重因子令m=2,根据KDPC部分得到的ci(0)开始循环迭代计算聚类中心集ci的值和隶属度矩阵uij的值,当目标函数稳定不变时终止迭代,根据最终得到的ci和uij划分数据集输出最后的聚类结果。
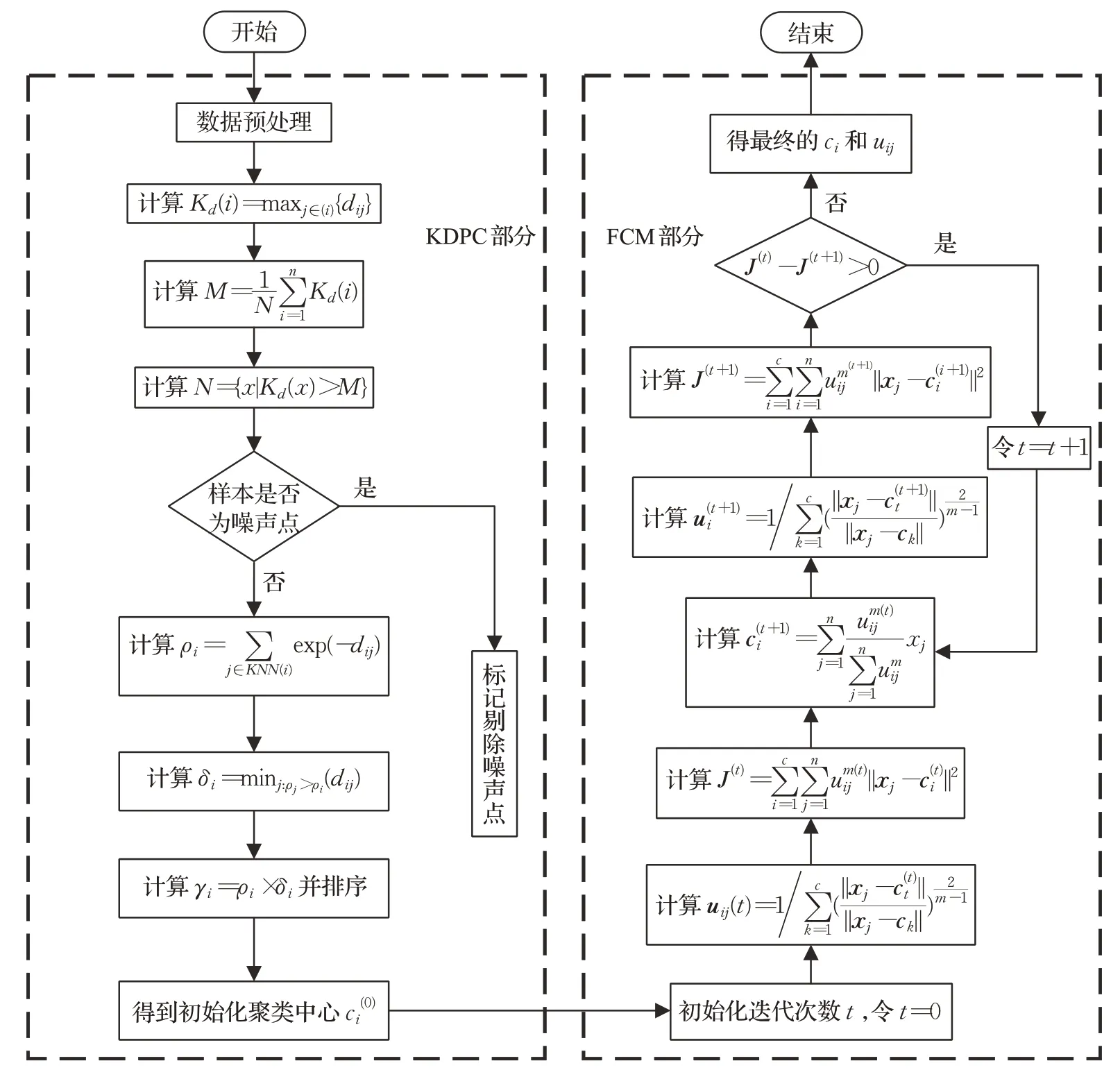
图1 KDPC-FCM算法总体流程图
3 实验分析
为了验证本文KDPC-FCM 算法的有效性,在加利福尼亚大学尔湾分校(University of California,Irvine,简称UC Irvine 或UCI)的机器学习数据库上的多个真实数据集和人造数据集上进行实验,对比算法有FCM聚类算法,以及文献[18]提出的DSFCM 聚类算法。采用Python进行仿真实验,各数据集的情况如表1所示。
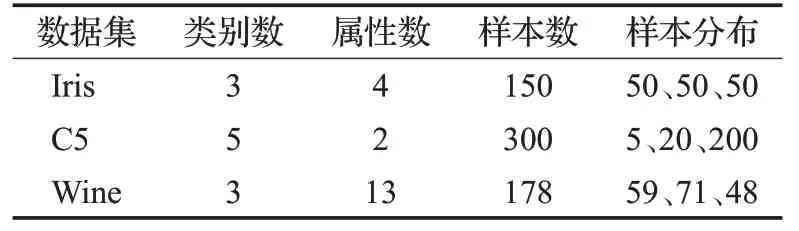
表1 各数据集的情况
其中,Iris 和Wine 数据集都是UCI 上的真实数据集,C5数据集是人造数据集。Iris数据集是鸢尾花样本分类数据集,包含4 个属性分别是:萼片长度、萼片宽度、花瓣长度和花瓣宽度;分为3 类:Setosa、Versicolour和Virginica,每个类别都有50个样本,共150个样本;C5数据集是个二维数据集,包含形状类似5 个圆的样本点,即5个类簇,每个类簇又由20个样本点组成,并且在这5 个类簇周围有200 个随机噪声点样本。Wine 数据集是葡萄酒分类数据集,由组成葡萄糖的13 种物质含量作为其属性,分为3 类:Class1、Class2 和Class3,分别包含59、71和48个样本。
3.1 初始化聚类中心对比分析
为了验证DPC的改进算法KDPC算法的有效性,运用KDPC 算法对Iris 数据集进行初始化聚类中心的选取,并与Iris数据集的实际中心作对比,如表2所示。
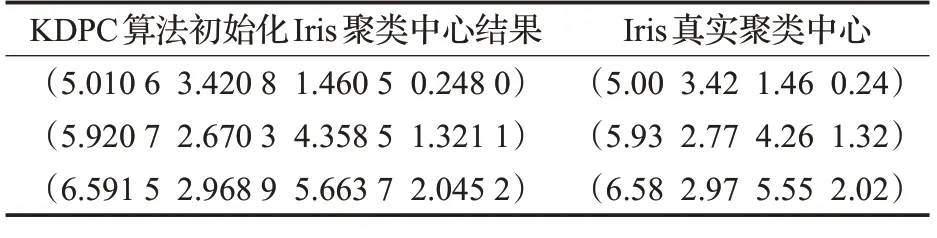
表2 初始化聚类中心对比
从表2可以看出,KDPC算法初始化Iris数据集聚类中心结果与Iris 数据集的真实聚类中心非常近似,误差在百分数级别,这证明了KDPC算法能够优化初始聚类中心的求取结果,为后续FCM 算法聚类打下了较好的基础,验证了KDPC算法的有效性。
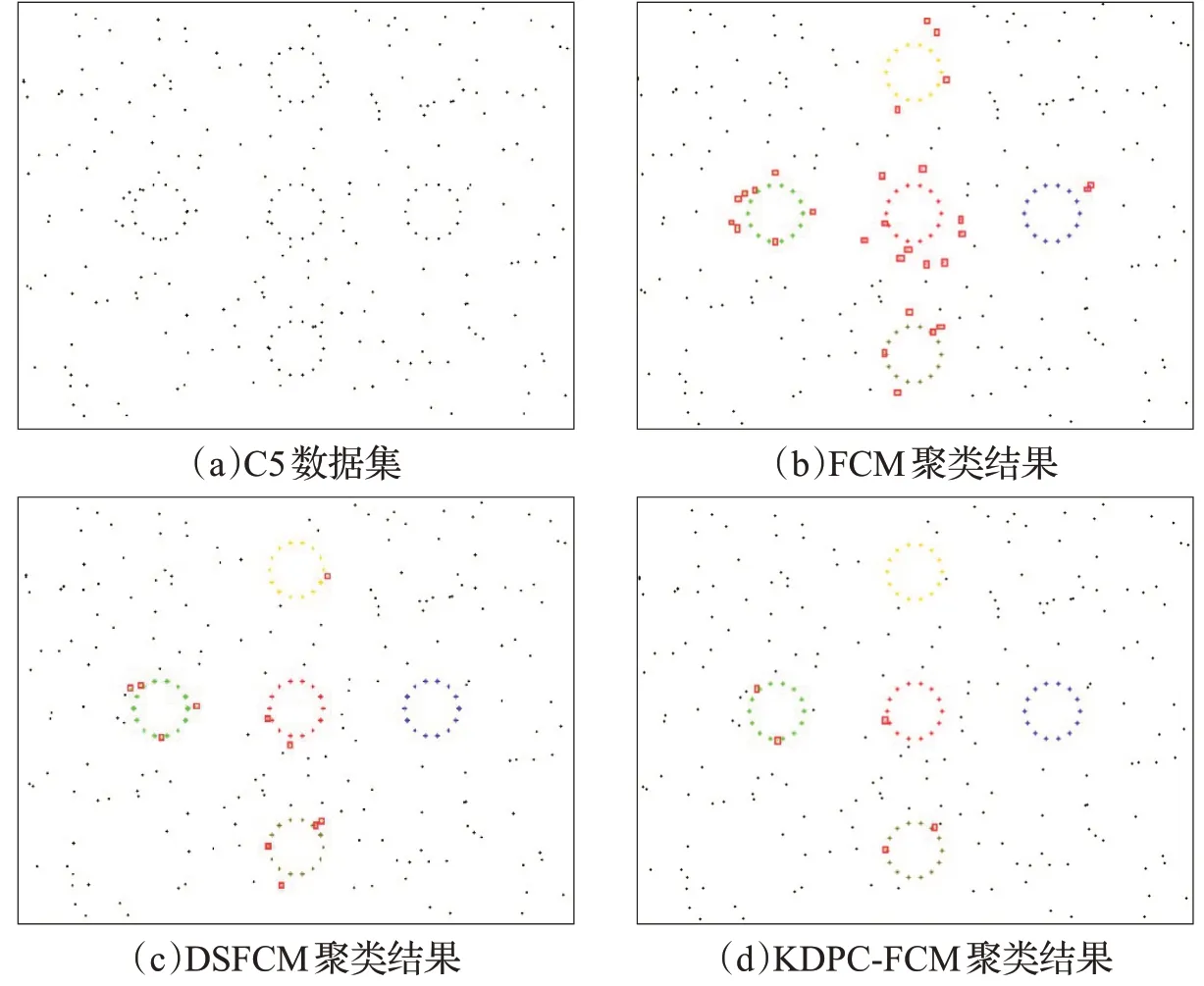
图2 C5数据集上各算法聚类结果图
3.2 抗噪性对比分析
C5数据集是本文人造数据集,由样本分布在5个半径都为0.2的圆上以及周围的随机噪声样本组成,其中5个圆是圆心点分别为(1,2),(2,2),(0,2),(1,3),(1,1)。样本的分布特征为每个圆上均匀分布20 个样本点,分布在5个圆周围的200个随机噪声样本点满足在5个圆之外,中心点位于(1,2)、宽为5高为4的矩形之内,并且服从均匀分布。具体分布情况如图2(a)所示。使用C5 数据集对FCM 算法、DSFCM 算法和本文提出的KDPC-FCM算法进行抗噪性对比试验。三种算法分别在该数据集上运行100次,观察记录其聚类结果。实验结果如下:FCM算法在100次聚类过程中,有23次实验聚类结果不理想,其中一次的聚类结果如图2(b)所示;DSFCM算法和本文KDPC-FCM算法在100次实验中都取得了不错的聚类结果,图2(c)和图2(d)分别为两种聚类算法的某一次聚类结果。
图2(a)中的每个黑色点代表着C5 数据集中的每个数据样本。图2(b)~(d)中的不同彩色点代表不同的类簇,即相同的颜色为一类,黑色样本点为识别出的噪声样本点,其中分类错误样本点被红色矩形框标注。图2(b)中有29 个样本点被标注红色矩形框,图2(c)和图2(d)分别有11个和5个样本点被标注。
实验结果分析:FCM 算法不仅将数据集外围的许多噪声样本进行了分类,其内部类簇数据样本点也存在着分类错误的情况,这是由于FCM 算法初始化隶属度矩阵uij是随机的,这导致了得到的初始化聚类中心也是随机的,一旦初始化聚类中心点选择不当,将导致聚类结果出现大量的错误分类;DSFCM 算法将一小部分靠近C5 最大的圆型类簇噪声样本进行了错误分类,总体聚类效果良好,这是由于DSFCM 算法采用了结合密度峰值和样本空间信息的方式来优化初始化聚类中心的选择,因此取得了较好的实验结果;KDPC-FCM算法仅将逼近圆样本的5个噪声样本误识别属于样本类簇,聚类效果较好,这是由于KDPC-FCM 算法在初始化聚类中心时,先对噪声进行了定义和识别,降低了噪声样本对聚类结果的影响。
从上述实验结果及分析可以得出结论:FCM 算法对噪声敏感,DSFCM算法和KDPC-FCM算法都具有良好的抗噪性,并且KDPC-FCM 算法要略优于DSFCM算法。
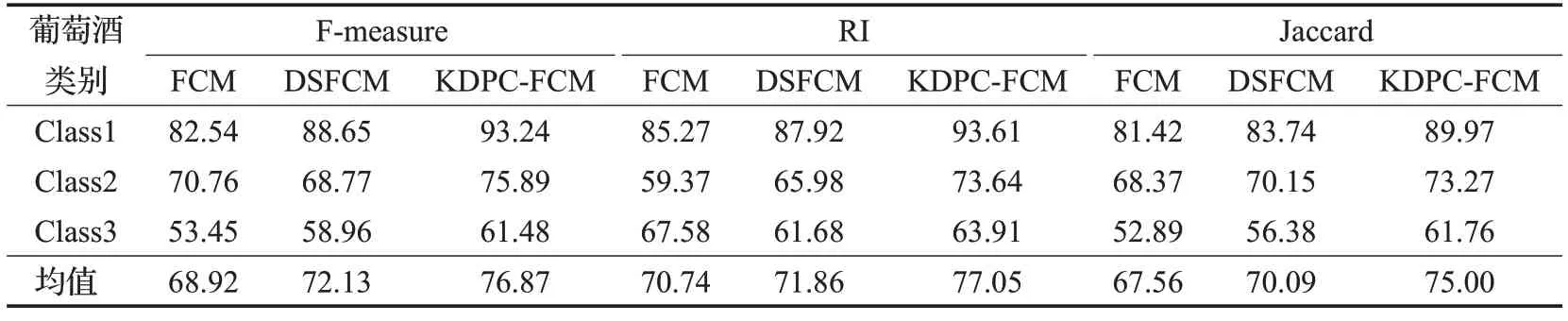
表3 Wine数据集上各聚类算法三种聚类评价指标值对比%
3.3 聚类效果及鲁棒性对比分析
为了验证三种算法的聚类效果及鲁棒性,本文采用UCI 数据库中的Wine 数据集进行仿真对比实验,该数据集同Iris 数据集一样,是聚类算法实验中常用的数据集。采用F-measure指标、兰德指数(Rand Index,RI)和Jaccard系数来评价三种算法在Wine数据集上的聚类效果,三项检测指标数越大证明聚类效果越好。
F-measure指标计算公式为:
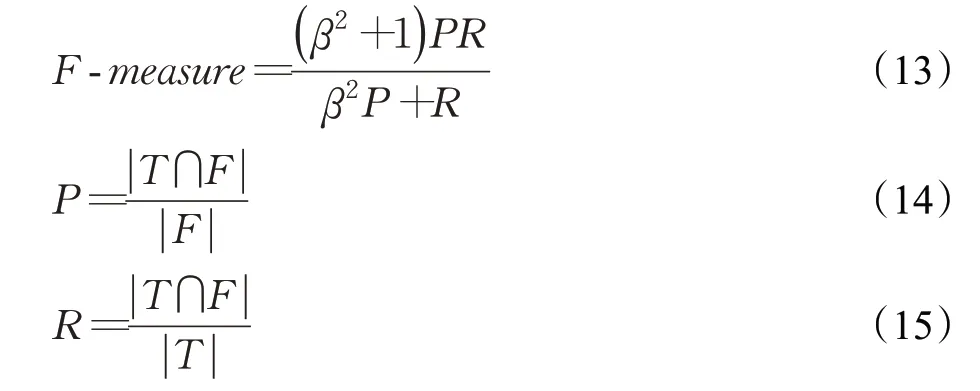
式中,β为参数变量,本文使用β=1 进行计算,P是精准率,R是召回率,F-measure 的取值范围为[0,1]。T表示数据集的真实分布,F表示算法聚类结果分布,P和R的取值范围均为[0,1]。
兰德指数及Jaccard系统计算公式为:
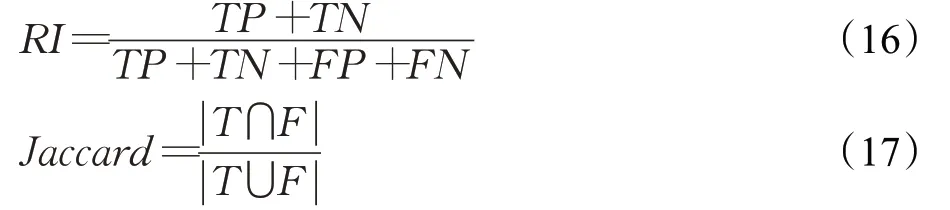
式中,TP表示同一类的样本被分到同一类簇的对数;TN表示不同类的样本被分到不同类簇的对数;FP表示不同类的样本被分到同一类簇的对数;FN表示同一类的样本被分到不同类簇的对数。RI和Jaccard的取值范围也都为[0,1]。
使用FCM算法、DSFCM算法以及本文KDPC-FCM算法分别对Wine 数据集进行聚类,使用上述三项聚类结果检测指标分别对三种算法的聚类结果进行检测运算,其检测的结果如表3 所示。从表中可以看出:在F-measure 指标下,FCM 算法在Class2 类别处的值要略高于DSFCM算法,其他类别均是KDPC-FCM>DSFCM>FCM;在RI指数下,FCM算法在Class3类别处的值要高于DSFCM 和KDPC-FCM 算法,其他类别均是KDPCFCM>DSFCM>FCM;在Jaccard 系数下,三类别均是KDPC-FCM>DSFCM>FCM。综合来看,在Wine数据集下总体各指标值均是KDPC-FCM>DSFCM>FCM,表明本文KDPC-FCM 在Wine 数据集下聚类效果方面要优于DSFCM和FCM算法。
为了检验三种算法的鲁棒性能,本文采用的方法是:将三种算法在Wine数据集上各进行50次运算实验,然后计算出每个算法在上述三种聚类评价指标的标准差,标准差越小,证明算法的波动性越小,稳定性和鲁棒性越强。经过实验的结果并运算得出各算法的标准差,三种对比算法在三种不同聚类评价指标上的标准差结果如表4所示。
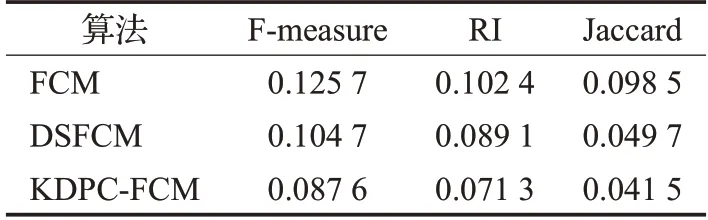
表4 各算法在各评价指标的标准差对比
从表4 的结果可以看出KDPC-FCM 算法的标准差在三种评价指标上均要小于其他两种算法,为了进一步验证KDPC-FCM 算法的聚类效果和鲁棒性,分别使用三种对比算法在表5所示的6个基准数据集上进行聚类实验。
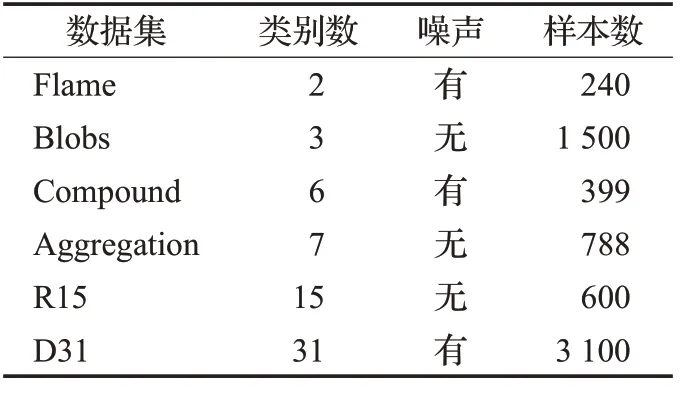
表5 各基准数据集
经过实验,在以上六种基准数据集上的聚类效果如图3所示。

图3 各算法在六种基准数据集上聚类效果对比图
图3中的不同彩色点代表不同的类簇,即相同彩色点为同一类簇,其中灰色点为识别出的噪声样本点。根据图3 可以看出,在Aggregation、R15 及D31 三种基准数据集上DSFCM 算法和KDPC-FCM 算法的聚类效果差不多,而FCM 算法聚类效果较以上两种算法效果较差;在Flame、Blobs 及Compound 三种基准数据集上,DSFCM算法要比FCM算法效果稍好一点,而KDPC-FCM算法的聚类效果最好。
综合在Wine数据集和六种基准数据集上的实验对比分析,可以得出初步结论:在三种对比算法中,FCM算法的聚类效果和鲁棒性较差,DSFCM算法次之,本文KDPC-FCM算法聚类效果和鲁棒性较强。
3.4 性能对比分析
为了对本文提出的算法进行性能对比分析,在不同规模的数据集上分别进行实验,用于实验的数据集如表6所示。
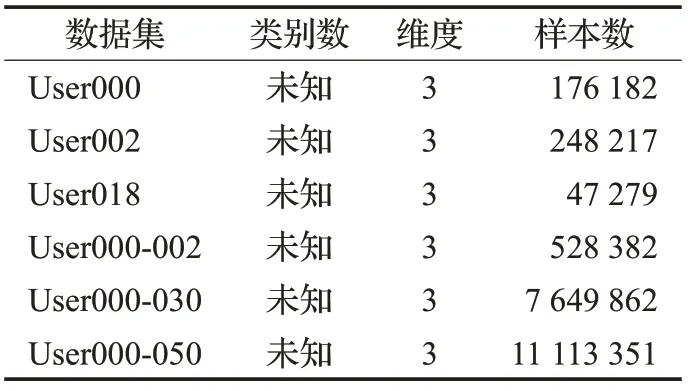
表6 性能对比实验数据集
User等6个的数据集来自微软亚洲研究院的Geolife项目[22]。该项目数据集包含182个用户在超过五年(2007年4月至2012年8月)时间里的户外活动。该数据集的GPS轨迹由一系列带有时间戳的点表示,每个点包含纬度、经度和高度信息。User000表示为使用了编号为000的用户所有活动数据,User000-002表示使用编号从000至002的三个用户的所有活动数据,其他数据集依次类推。
采用Geolife项目数据集测试数据规模对性能的影响实验,即表6 中的6 个User 数据集,分别使用FCM、DSFCM以及本文KDPC-FCM算法在这6个数据集上进行聚类,并记录在每个数据集上运行的时间,得到如表7所示的实验结果。
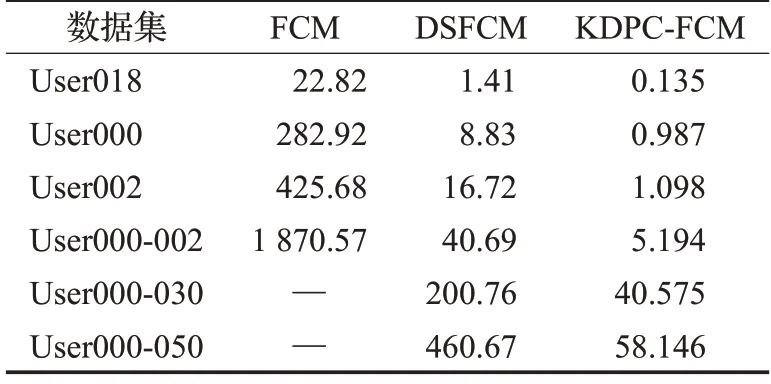
表7 规模性能实验结果s
由于本文主要是针对FCM 算法进行对比分析,因此表7 中KDPC-FCM 的实验结果并未加上KDPC 运行的时间。
从表7 可以看出,随着数据集的样本数的规模增加,三种算法的时间也随之增加,且KDPC-FCM算法的聚类速度明显要快于其他两种算法,且随着数据集的样本数量达到百万级别时,FCM 算法的聚类时间将非常漫长,本文由于时间限制,用“—”表示其时间暂时无法计算,而DSFCM和KDPC-FCM算法在数据达到千万级别时,速度仍比较快,且KDPC-FCM算法保持在1 min内。
4 总结
本文针对FCM 算法对噪声点敏感、容易局部收敛等问题,提出了融合KNN优化的密度峰值和FCM聚类算法KDPC-FCM,该算法先将噪声样本识别去除后,在使用引入的样本的K近邻信息来计算样本的局部密度,对DPC算法进行了改进,使得初始化中心点更加接近真实数据中心点,从而使得FCM算法可以更加精准快速地得到较好的聚类结果。为了验证算法的有效性,本文在UCI中的多个数据集、一个人工数据集、多个基准数据集以及微软亚洲研究院的Geolife项目数据集上进行实验,并与传统FCM算法和DSFCM算法进行了对比分析,得出结论:KDPC-FCM算法能够有效提高聚类的抗噪性、准确性和全局收敛能力,达到了较好的聚类效果。
