X80管线钢不同变形状态的磁记忆检测试验研究

杨晓惠, 谭川东, 唐名杰, 周鹏伍, 唐义超, 刘艳军

(西南石油大学 机电工程学院，成都 610500)

油气管道在国家经济运行和人们日常生活中发挥着极其重要的作用。统计发现，油气管道的破坏主要源于各种微观和宏观的应力集中[1]。其中，塑性变形被认为是材料在破坏前必经的一个特殊阶段，可以看作是材料在应力作用下的一种早期损伤状态。因此，进行管道的塑性变形检测，可以实现对管道损伤的早期预警，以保证油气运输管道高效安全的运行。

20世纪末兴起的金属磁记忆检测技术，是一种通过检测铁磁性材料在地磁场和应力作用下的磁记忆信号，来发现应力集中和缺陷损伤的无损检测方法[2-3]。利用磁记忆检测实现塑性变形诊断是一项新技术，目前对这一技术的研究还很有限。在试验研究方面，由于采用的检测设备不同，磁记忆信号在不同变形阶段的表现特征存在许多差异，磁场分量的选择也有不同观点。Dong等[4]研究了18CrNiWA钢在弹塑性变形阶段的磁记忆信号法向分量的变化规律，发现斜率在屈服极限时达到最大值；易术春等[5]通过对Q345B钢静载拉伸实验研究，建立了法向磁场梯度指数与应力的量化关系；李云飞等[6]研究了X80管线钢拉伸载荷下的磁记忆信号的法向和切向分量特征，以及与塑性损伤程度之间的关系。目前，多数研究工作集中在拉伸载荷作用下法向磁场分量的特征研究，但对切向分量的研究鲜有报道。在磁记忆机理研究方面，利用J-A理论模型来描述弹性变形已得到广泛认可，但由于塑性变形对磁化的影响因素非常复杂，不同学者也提出了不同的理论模型。Sablik等[7]利用残余应力来替换作用应力，对J-A模型进行了改进；Wang等[8]提出了磁有效场的塑性变形分量，得到非滞后磁化强度与塑性应变之间的定量关系；刘清友等[9]在对比分析多种塑性变形磁化模型表达式的基础上，推导出塑性变形的修正磁化模型。可见，塑性阶段的力-磁定量关系目前尚无统一定论。

针对以上问题，本文通过X80管线钢的静载拉伸试验，得到在弹塑性变形状态下试件表面的磁信号变化规律，研究了相应的力磁耦合机理，建立了特征参数与应力的量化关系，以期为塑性变形损伤的诊断和预测提供一定的理论基础。

1 金属磁记忆检测原理

金属磁记忆检测是以地磁场作为励磁源的一种弱磁检测技术，其基本原理是：在地磁场和外应力的共同作用下，铁磁构件应力集中区的内部磁畴，发生具有磁致伸缩现象的磁畴晶格组织定向和不可逆的重新取向，并在应力与变形集中区形成附加磁极[10]，宏观显示为构件周围磁场的异常，即应力集中区的磁信号切向分量出现极值，法向分量改变符号且在异常区具有零值[11]，如图1所示。由于金属内部存在内耗效应(粘弹性，位错内耗等)，使得外应力消除后，这种磁状态的不可逆变化继续保留。因此，通过对构件表面磁场的检测，可以对其应力集中情况进行定位和评价，从而达到早期诊断的目的。

图1 磁记忆检测原理图

2 试 验

2.1 试验材料

试验采用国内某钢厂生产的X80管线钢，其主要化学成分如表1所示。通过拉伸性能测试，得到材料的力学性能参数如表2所示。根据GB/T228.1-2010加工的标准板状试件尺寸如图2所示。为减少测量路径和提离值对磁记忆信号的影响，在标准板状试件上布置限位块和扫描线。

表1 X80管线钢的化学成分(质量分数/%)

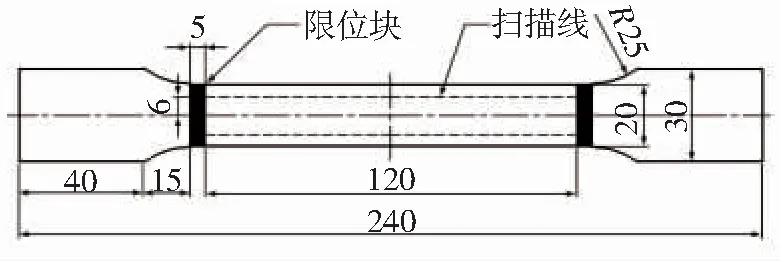
图2 检测试件示意图(单位：mm)

2.2 试验设备及方法

为避免试件在加工过程中造成的应力集中对试验结果产生影响，采用TC-3台式退磁器对试件进行退磁处理。静载拉伸试验在MTS-809.25疲劳试验机上完成，采用逐级加载的方式进行施载，达到预定值后，保载10 s再取下试件，用TSC-2M-8磁记忆检测仪进行试件表面磁场强度扫描，测试提离值保持2 mm不变，测试方向和地磁南北极方向垂直。依此重复，直至试件被拉断。

3 试验结果

为了消除测试误差，选用3组相同试样，在相同测试条件下进行了重复试验。通过数据分析发现，各试件的磁场分量信号，以及同一试件两条扫描线上的磁场分量值均具有很高的相似度。因此，选取其中一个试件作为研究对象，其检测结果取两条扫描线上磁场分量值的平均值。

3.1 载荷与变形阶段的关系

拉伸试件的载荷应变曲线如图3所示。在加载过程中，试样经历了弹性变形-屈服-塑性变形的不同阶段。根据载荷(F)-应变(ε)曲线，可以初步确定拉伸载荷与变形阶段的对应关系。但在逐级加载试验中，反复加载将导致试件疲劳积累，使得屈服载荷发生变化，而无法准确划分变形阶段。通过记录拉伸试件加载时和卸载后的位移，可得到试件的载荷(F)-伸长量(ΔL)曲线，如图4所示。

图3 试件的载荷-应变曲线

图4 试件的载荷-伸长量曲线

试件伸长量随载荷变化的过程明显分成两个阶段：当载荷F≤35 kN时，试件的总伸长量较小，卸载后的残余伸长量几乎为零，表现出弹性变形特征；当载荷F≥42 kN时，试件的总伸长量和残余伸长量均随载荷的增加而显著增大，表现出塑性变形特征。结合图3和图4的检测结果，在弹性变形阶段选取的拉伸载荷分别为5、10、20、30和35 kN；在塑性变形阶段选取的拉伸载荷分别为42、44、50 和55 kN。

3.2 载荷对磁场分量的影响

3.2.1 弹性阶段

对试件逐级加载至预定载荷，卸载后进行磁记忆检测，获得了不同载荷下试件表面的磁场强度分布曲线。如图5所示，在弹性变形阶段，随扫描位移量Lx的增加，磁记忆信号的法向分量H(y)和切向分量H(x)均表现为线性程度较好的直线。由于材料内部应力分布相对均匀，因此，各载荷作用下的磁场强度分布曲线具有相似特征。其中，法向分量H(y)表现为倾斜的直线，随载荷的增加逆时针偏转，逐渐变陡；切向分量H(x)表现为水平直线，随载荷的增加逐渐下移。

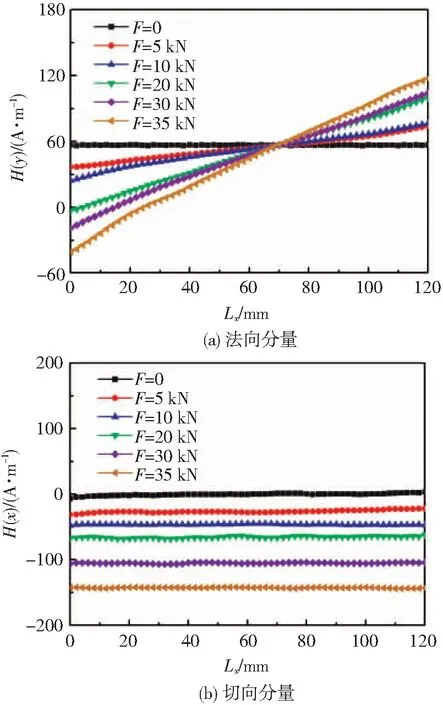
图5 弹性变形阶段载荷对磁信号的影响

3.2.2 塑性阶段

为进一步研究X80管线钢在塑性变形状态下的磁记忆信号变化规律，分别检测了试件逐级加载后的表面磁场强度。如图6(a)所示，各载荷作用下的H(y)曲线团聚在一起，随着拉伸载荷的增加，其斜率略微减小，相比于弹性阶段的磁信号出现了反转现象；H(y)曲线在Lx=10～30 mm区域内出现了不同程度的波动。进一步研究法向分量的梯度K(y)(图6(b))，发现在该区域存在明显的不均匀变化，说明此处存在磁场强度的畸变。如图6(c)所示，切向分量H(x)在各载荷作用下的曲线近似于水平直线，随着拉伸载荷的增加而逐渐上移，并在Lx=10～30 mm区域内出现明显弯曲，其变形程度随载荷的增加而增大。切向分量的梯度K(x)曲线在此范围内表现出过零点特征(图6(d))。由Doubov教授的判据[3,11]可知，试件出现了明显的应力集中情况。观察试件表面发现，在Lx=10～30 mm区域内出现明显的滑移线，这是塑性变形的应变痕迹。上述试验现象说明，磁场强度分布曲线的畸变区域与试件的塑性变形区相对应。

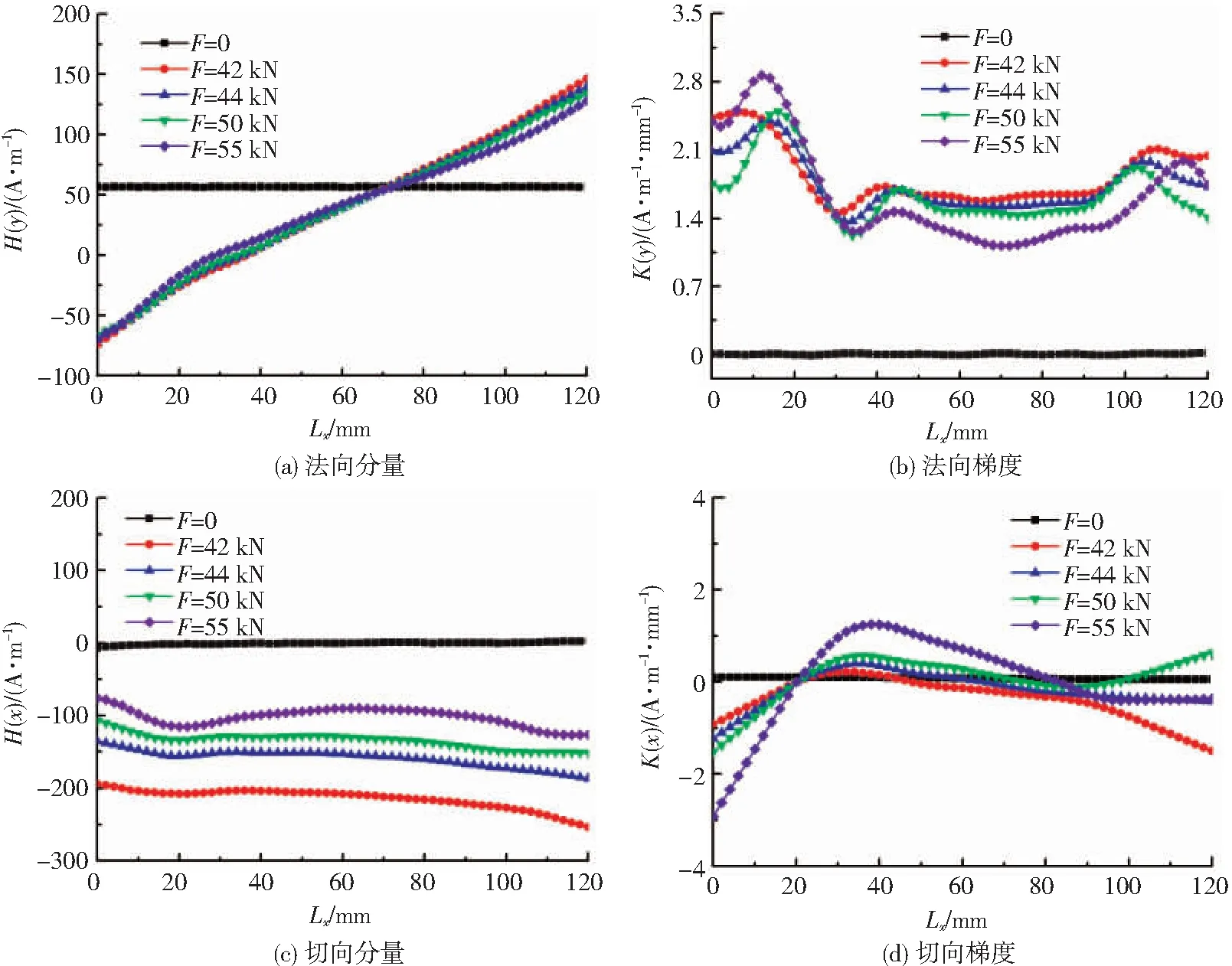
图6 塑性变形阶段载荷对磁信号及其梯度的影响

3.3 应力与特征参数的关系

根据3组重复试验的检测结果，分别提取磁场强度法向分量的斜率Ks(y)和切向分量的绝对值|H(x)|，绘制两特征参数与拉应力σ的关系曲线，结果如图7、图8所示。由图7、图8可以看出，Ks(y)和|H(x)|随拉应力σ的变化规律表现出相似的特征：弹性变形阶段，两个特征参数随应力的增加而快速增大；达到屈服强度时，二者均出现最大值；塑性变形阶段，Ks(y)随应力的增加缓慢降低，而|H(x)|则随应力的变化急剧减小。其中，参数Ks(y)在弹塑性变形阶段发生反转的现象，与董世运课题组[12]的研究结果一致。

图7 Ks(y)与拉应力的关系曲线

图8 |H(x)|与拉应力的关系曲线

通过对磁记忆信号试验数据的分析，建立了塑性变形损伤区Lx=10～30 mm范围内磁场分量梯度最大值Kmax与应力σ的关系曲线，如图9所示。

Kmax=max(|Ki|)

(1)

式中，Ki为第i个测试点的磁场分量梯度值。

由图9可知，法向分量的Kmax(y)在弹性阶段随应力的增加而快速增大；进入塑性阶段后，Kmax(y)的增大趋势变缓；随着应力的进一步增加，试件的应力集中和变形程度加剧，Kmax(y)快速增大。这一变化趋势与文献[5]的检测结果相似。切向分量的Kmax(x)在弹性阶段随应力的增加而缓慢增大；进入塑性阶段后，Kmax(x)急剧增大。

图9 Kmax与拉应力的关系曲线

4 分析与讨论

由上述试验现象可以发现，在不同载荷作用下，磁记忆信号的变化趋势具有明显的不同，应力对试件内部磁畴和磁化矢量的变化情况影响如图10所示。

4.1 弹性阶段分析

在弹性变形阶段，拉应力将促使铁磁材料内磁畴组织重新排列和磁化矢量转向，见图10，表现为试件在应力轴线方向上的均匀磁化，在地磁场作用下对外显示磁性。因此，沿轴线方向检测时，磁场强度法向分量H(y)过零点，表现为倾斜的直线，而切向分量H(x)为水平直线。

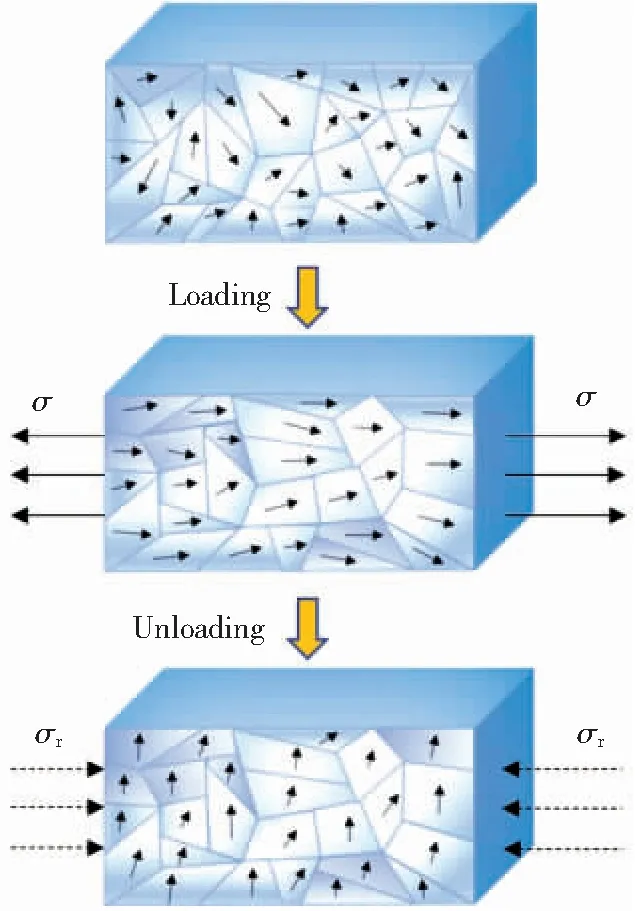
图10 应力对磁畴的影响示意图

基于磁畴理论和畴壁运动建立的J-A模型认为，单轴拉应力对铁磁性材料表面磁化强度的影响，相当于对其内部的磁畴结构施加一个等效磁场[13]。弹性变形阶段材料表面的有效磁场Htotal可表示为

Htotal=H+αM+Hσ

(2)

式中：H为外磁场；α为磁畴耦合系数；M为材料的实际磁化强度；Hσ为应力产生的等效磁场，可表示为

(3)

式中:σ为外应力；μ0为真空磁导率；λ为磁致伸缩系数，由于λ是M的偶函数[14]，所以当M较小时，可令λ=bM2，b为材料的相关系数；θ为外应力σ与外磁场H间的夹角；ν为泊松比。

令l2=cos2θ-νsin2θ，将式(3)带入式(2)可得

(4)

由式(4)可知，在一定磁化强度下，外应力越大，有效场越大，其磁记忆信号也越强。因此，当拉伸载荷增加时，法向分量的斜率Ks(y)和切向分量的绝对值|H(x)|均增大。

4.2 塑性阶段分析

管线钢在制造过程中，其内部难免存在杂质和缺陷。在较大的塑性变形状态下，这些缺陷区域内原有的磁畴组织将发生部分破坏和分割，形成高磁阻区，使原本均匀的磁力线发生畸变。因此，磁记忆信号的法向和切向分量在局部塑性变形区均出现了异常波动。另一方面，随着塑性变形量增大，试件内部的残余应力增加，位错密度迅速积累，阻碍了磁畴的有序化运动；同时，塑性变形卸载后的残余压缩应力，将驱使磁化矢量沿着压应力的垂直方向转动，见图10。这些微观结构上的变化都将导致试件表面的磁场强度降低。

根据畴壁运动和位错钉扎理论，铁磁性材料发生塑性变形后，其表面的有效场应包括：外加磁场、残余应力场、塑性应变场和退磁场4部分[15]。因此，塑性变形阶段材料表面的有效磁场Htotal可表示为

(5)

在塑性阶段卸载后，将会有残余应力留存，其磁性响应特性与外加应力等同，由式(3)得残余应力对有效场的影响，

(6)

式中σr为应力卸载后，由于晶粒的各向异性、晶粒内外的塑性变形等因素引起的残余应力。

试样经过塑性变形卸载后，材料内部留存的塑性能也会产生一定的等效场分量，而这一部分能量可以和钉扎作用相联系[16]。塑性变形产生的等效磁场为

(7)

式中:εp为塑性应变量；系数k=b<∈π>/2μ0m；∈π为畴壁上的钉扎能，与材料属性有关；m为磁畴磁矩。

残余压缩应力作用下的磁化矢量方向与外加磁场方向相反，将导致明显的退磁效应。基于这种现象，Schneider提出了应力退磁因子[17]，表示为

(8)

式中:λs为饱和磁滞伸缩系数；Ms为饱和磁化强度；Bs为饱和磁感应强度。

将式(6)、(7)、(8)带入式(5)中得

(9)

式(9)表明，随着塑性变形量的增加，残余应力增大，有效场逐渐减小，磁记忆信号由强变弱。因此，随着拉伸载荷的增加，法向分量斜率Ks(y)和切向分量的绝对值|H(x)|均减小。

4.3 特征参数分析

由上述的力磁耦合模型分析可得，当材料由弹性变形向塑性变形转变时，磁化强度由大变小，出现反转现象。特征参数Ks(y)和|H(x)|随应力的增加先增大后减小，其变化情况直观地表现了材料的弹塑性转变过程。但|H(x)|的极值特征更加明显，随应力的变化更加显著，说明|H(x)|与变形状态之间存在较好的相关性。因此，可以利用|H(x)|的极大值，来判断试件是否进入塑性变形状态。

随着应力的增加，磁场分量梯度最大值Kmax(y)和Kmax(x)分阶段持续增大，其数值大小直接反映了试件的应力集中状态和塑性变形程度。特别是切向分量Kmax(x)在塑性阶段随应力的增加而急剧增大，表明其对应力的变化比法向分量更敏感。采用指数拟合法得到图9中曲线Kmax(x)与应力σ的量化关系.

Kmax(x)=0.164+0.003exp(-σ/112.248)

(10)

R2=0.989 54

(11)

式中R为拟合相关系数。

由式(10)可以看出，在试验条件下，X80管线钢的应力状态与磁场切向分量梯度呈非线性的定量关系。这种关系在一定程度上可为X80管线钢构件塑性损伤的无损评价提供参考依据。

5 结 论

1)弹性阶段磁场法向分量H(y)曲线近似为斜直线，切线分量H(x)为水平直线，随着应力的增加，H(y)的斜率和H(x)的绝对值均增大；塑性阶段，两者均减小。

2)建立了弹性阶段的有效场力磁耦合模型，在此基础上引入塑性应变场和退磁场，建立了塑性阶段的有效场力磁耦合模型。这些模型可以解释磁信号发生反转的现象。

3)切向分量对局部塑性变形的表征比法向分量更为敏感。以切向分量的绝对值|H(x)|为特征参数，其随应力变化的反转变化趋势，可作为识别弹塑性变形状态的依据。

4)建立了切向磁场梯度最大值Kmax(x)与应力σ的量化关系，利用Kmax(x)值可以表征试件的应力集中程度。