耦合拐点偏移修正的Boltzmann函数预计模型及其参数反演方法

江克贵，王 磊，池深深，魏 涛，蒋 创

( 1. 安徽理工大学 测绘学院，安徽 淮南 232001；2. 中国矿业大学 环境与测绘学院，江苏 徐州 221116 )

我国能源资源禀赋具有“富煤、贫油、少气”的特点。据预测，即使到2030年煤炭资源仍占中国能源需求的50%以上[1]。大规模高强度的煤炭资源开发会引发一系列矿山地质环境灾害问题，如含水层破坏、山体滑坡、地表塌陷和建构筑物损毁等。开采沉陷预计理论在评估潜在地质灾害，分析矿区沉降机理方面具有至关重要的作用，因而开采沉陷预计及防治的相关技术与理论一直是我国矿山领域的研究热点，基于实测资料求取精准、可靠的开采沉陷预计参数也是预计模型应用过程中的难 点。

常规概率积分法存在以下几个问题：沉降变形预计曲线边缘收敛过快，与实际变形情况有较大差别；不能较好地适用于复杂多样地质采矿条件下的地表沉陷预计，不具有广适应性；联合时间函数的动态沉陷预计模型仍然存在一些问题。解决上述问题可以从2个途径入手：① 构建精准广适应的开采沉陷预计方法；② 提高预计参数的准确性和可靠性。对于途径①，相关学者提出了新的开采沉陷预计方法或进行一定程度的改进。一类是针对不同地质采矿条件而提出的沉陷预计方法，戴华阳[2]等提出了地表移动的矢量预计法，为解决大倾向煤层开采沉陷问题提供了预计依据；郭文兵[3]提出了全采工作面叠加预计方法，提高了深部大采宽条带开采预计精度；文献[4-6]提出了形式各异的开采沉陷预计方法，在一定程度上解决了多种不同地质采矿条件下的开采沉陷预计问题。另一类是针对改进时间函数的动态开采沉陷预计方法，根据地表移动变形规律和采动程度，文献[7]建立了一种新的Knothe时间函数求参模型，提高了地表动态下沉预测的准确性和可靠性；文献[8]采用整体偏移修正和生长函数模型相结合的方法对时间函数进行优化，进一步提高了地表下沉动态预计的精度。近年来，一些学者基于Boltzmann函数提出了新的开采沉陷预计模型[9]，通过分析函数曲线形态和参数特点发现，与概率积分法相比，Boltzmann函数在曲线边缘部分收敛缓慢，且其预计模型参数与概率积分法模型参数可以相互转化；另外，研究表明，该模型能够广适应于不同开采条件下的地表沉陷预计[10]。鉴于此，在Boltzmann函数的基础上，笔者借鉴概率积分法模型的推导经验，通过理论分析，探讨拐点偏移修正方法[11]，构建了一种耦合拐点偏移修正的Boltzmann函数预计模型。

针对途径②，大量学者把智能优化算法引入 到开采沉陷预计参数求取中来，相对于传统方 法[12-14]，避免了求参速度慢、对初值依赖性强、易陷入局部最优值、抗差能力差等缺陷，极大地提高了求取参数的准确性和可靠性。其中比较典型的有模矢法[15]、遗传算法[16]、粒子群算法[17-18]等。笔者拟将FWA( Fireworks Algorithm )应用于反演预计模型参 数，提出了一种耦合拐点偏移修正的Boltzmann函数模型参数反演方法，并对该方法的抗差性能进行讨论。

1 模型原理

玻尔兹曼( Boltzmann )函数模型在应用实践中得到了广泛的发展[19-20]。分析发现，Boltzmann函数可以生成一个S形曲线，跟半无限开采地表变形盆地主断面的下沉曲线形态相似。对非充分开采、充分开采以及超充分开采的实测结果分析表明，Boltzmann函数可以较好地预计不同开采程度下的地表开采沉陷。基于Boltzmann函数的半无限地表变形盆地主断面的下沉预计公式为

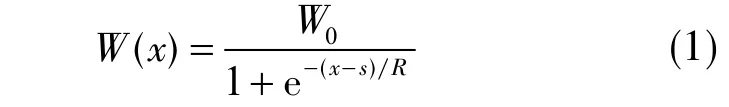
式中，W0=mq cos α，其中，m为煤层采厚，q为下沉系数，α为煤层倾角；R为新的主要影响半径，与主要影响半径r的物理意义相同，其主要影响下沉曲线的分布形态；S为拐点偏移距。

统计分析发现[14]，R≈r/4.13，其中，r=H/tan β，H为煤层采深，tan β为主要影响角正切。并且当x→∞时，有W( x )→W0；当x=s时，W( x )=W0/2；这些结果都符合开采沉陷一般规律。

对式( 1 )求微分，可得Boltzmann函数预计模型的单元影响函数，即

根据概率积分法的推导经验和弹性力学知识，可得单元水平移动函数为

对单元水平移动函数进行积分，可得地表沿x方向的水平移动为

令b'=B/R，统计分析可得b'=4.13b，则

式中，B为常数；b为水平移动系数。

煤壁附近采空区上方顶板会出现悬顶或过度破坏垮落，其作用效果相当于工作面采空区两端煤壁向内或向外分别平移了S的距离。文献[11]表 明，概率积分法将拐点偏移距的影响全部加在了终采线和倾向上山处；由此，根据实测数据拟合求取的开采沉陷预计参数会因为拟合度低而出现偏差较大的现象。针对此问题，在Boltzmann函数预计模型的基础上对拐点偏移进行修正，走向和倾向主断面有限开采下沉和水平移动计算公式分别为

式中，

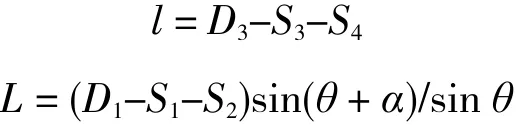
其中，D3和D1分别为工作面走向和倾向开采长度； S1，S2，S3，S4分别为工作面倾向下山、倾向上山、开切眼和终采线拐点偏移距；θ为开采影响传播角。

井下开采尺寸为D3×D1的工作面引起地面任意一点( x，y )沿φ方向( x轴的正向逆时针到指定方向的角值 )的下沉和水平移动分别为

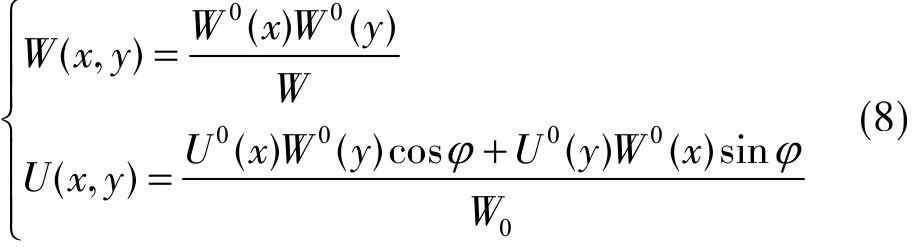
综上所述，模型预计参数为

地质采矿参数为

式中，ϑ为工作面倾向方位角，直接参与工作面坐标转换的过程。

构建模型的概化如式( 9 )所示，工作面地质采矿参数和模型预计参数作为输入变量控制地表相应预计点的形变；相反，当地表监测点的形变获取后，在工作面地质采矿参数已知的情况下，求取精确可靠的模型预计参数显得尤为重要；同时构建模型属于高度非线性模型。因此，本文引入一种FWA。

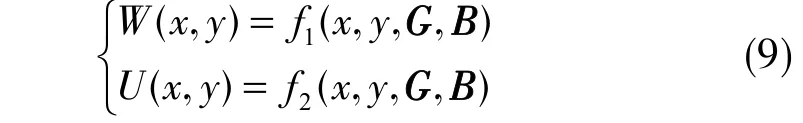
2 模型参数反演方法

2.1 FWA

FWA是受到夜空中烟花爆炸的启发而提出的一种具有局部搜索能力和全局搜索能力自调节机制的群体智能算法[21]。FWA的性能取决于爆炸算子( 即爆炸产生火花操作 )、变异算子( 高斯变异产生火花操作 )、映射规则( 映射到指定范围操作 )和选择策略( 选择下一代火花操作 )[22-23]。

( 1 ) 爆炸算子

爆炸算子是FWA的核心组成部分，它由爆炸数目、爆炸半径、位移操作3部分组成。假设烟花种群大小为N，对于烟花xi，其爆炸数目和爆炸半径的计算公式分别为

式中，Di为第i个烟花爆炸产生的火花数目；D为常 数，用来调整产生的爆炸火花数目；f( xi)为第i个烟花的适应度值；ymax为当前种群中最大适应度值，ymax=max( f( xi) )；ξ为一个机器最小量，用来避免除零操作；Ai为第i个烟花的爆炸半径；A为常数，用来调整爆炸半径的大小；ymin为当前种群中最小适应度值，ymin=min( f( xi) )。

为了避免适应度较好的烟花位置产生过多的爆炸火花，同时适应度较差的烟花位置产生过少的爆炸火花，对爆炸的火花数目进行如下限制：

式中，a，b为常数；round( )为根据四舍五入原则的取整函数。

位移操作是对烟花的每一维进行位移，即

式中，rand( 0，Ai)表示在幅度Ai内生成的均匀随机 数；xik为第i个烟花在第k个维度上的位置信息。

( 2 ) 变异算子

为了进一步增加种群的多样性，FWA在随机选择的烟花中执行高斯变异操作，即

式中，Gaussian( 1，1 )表示高斯分布。

( 3 ) 映射规则

爆炸算子和变异算子产生的火花可能会超出边界，利用映射规则将超出域值的火花映射到一个新的位置。

( 4 ) 选择策略

在候选者集合中( 包括烟花、爆炸火花和高斯变异火花 )，适应度最好的个体会首先被确定性地选择到下一代作为烟花，剩下的后代烟花采用轮盘赌法进行选择。候选者xi被选择的概率计算公式 为

式中，R( xi)为当前个体xi与其他个体的距离之和； d( xi，xj)表示任意2个个体xi和xj之间的欧氏距离；xj∈K表示第 j个位置属于集合K。

2.2 方法构建

综合地表移动变形、预计模型以及FWA原理，提出了一种耦合拐点偏移修正的Boltzmann函数模型参数反演方法( BFWA-MSPP )，具体步骤如下：

( 1 ) 数据准备。首先，利用地表移动观测站观测目标区域地表进入稳定期后的下沉和水平移动量，获取工作面地质采矿条件参数；然后，选取适当的FWA参数，确定开采沉陷预计参数取值空间，进而生成烟花初始种群。

( 2 ) 适应度评价。烟花初始种群用作迭代种 群；基于构建的Boltzmann函数预计模型，结合获取的地质采矿条件，第i组开采沉陷参数预计目标区域任意点 j的下沉和水平移动分别为 Wpi,j和 Upi,j；假设地表点 j的实测下沉和水平移动值分别为 Wmj和Umj，以预计值和实测值之差绝对值的和为准则进行适应度评价，适应度的构造如式( 17 )所示；然后判断是否满足迭代终止条件，如果满足，输出最优解，否则执行步骤( 3 )。

( 3 ) 生成火花。根据烟花迭代种群的适应度，结合FWA参数，计算每个烟花的爆炸半径与爆炸火花数目；利用式( 13 )对各个烟花进行位移偏移，生成多个爆炸火花；另外，在烟花种群中，利用变异算子生成多个变异火花。

( 4 ) 映射及后代选择。利用映射规则把超出预计参数范围的火花映射到可行域范围内。根据选择策略，在候选者集合中选择下一代。

( 5 ) 循环执行步骤( 2 )～( 4 )，直到满足终止条件，输出最优开采沉陷预计参数，模型参数反演方法技术 路线如图1所示。

图1 BFWA-MSPP技术路线 Fig. 1 Technology roadmap of BFWA-MSPP

3 仿真试验

3.1 数据模拟

以淮南矿区煤系地层为背景，模拟工作面上覆岩层岩性为中硬，工作面地质采矿条件为：煤层采高m=3 m，煤层采深H=400 m，煤层倾角α=5°，工作面倾向方位角ϑ=0°，工作面开采尺寸D3×D1=800 m×200 m。分别沿工作面走向和倾向主断面 模拟布设了2条监测线E和N，测点间距为30 m，共 布设88个监测点，模拟的工作面和布设的监测线 如图2所示。基于构建模型和模拟的开采沉陷预计参数( 表1 )预计开采沉陷稳定后的下沉和水平移 动。

3.2 反演试验

根据模拟的地质采矿条件和预计的形变数据，利用本文构建的BFWA-MSPP进行开采沉陷预计参数反演试验，求参结果见表1。

从表1可以看出，反演参数q，tan β，b，θ的相对误差最大不超过1.2%，中误差最大不超过1.2；反演拐点偏移距S的相对误差和中误差分别控制在6.2%和6.5 m以内；此外，BFWA-MSPP拟合下沉和水平移动误差为-11.6～5.7 mm，中误差为±6.1 mm。试验结果表明，构建的方法可以准确可靠地求取开采沉陷预计参数。

图2 模拟工作面和监测线示意 Fig. 2 Schematic diagram of simulated the working face and the observation lines

表1 仿真试验BFWA-MSPP求参结果 Table 1 Solved results of BFWA-MSPP for simulation experiment

3.3 抗差试验

在实际测量中，观测值会不可避免地掺入一些随机误差和粗差[24-25]，随机误差和粗差的存在势必影响求参结果的质量。为了探讨BFWA-MSPP抵抗观测误差的能力，基于3.1节的模拟数据，设计试验如下：在所有监测点的下沉值和水平移动值中分别加入均值为0、标准差为30 mm和10 mm的高斯噪 声；在此基础上，将所有监测值再加入-200 ～200 mm( 服从均匀分布 )的粗差；然后，以包含测量误差的数据为观测值，利用BFWA-MSPP进行求参，求参结果见表2。

表2 BFWA-MSPP抗差求参结果 Table 2 Anti-error result of BFWA-MSPP

从表2可以看出，在所有观测点加入观测误差后，反演q，tan β，b，θ的相对误差不超过13%，反演 拐点偏移距S的相对误差控制在32%以内；就拟合效果来看( 图3 )，在含有观测误差干扰的情况下，拟合曲线和模拟观测曲线较吻合。需要说明的是，本 文为了极限测试算法的稳定性加入了较大的误差，但在工程实践中很少有如此大的观测误差( 通过精密测量仪器和数据处理方法，观测误差可以得到控制 )。试验结果表明，BFWA-MSPP可以有效抵抗观测误差的影响，在监测实施困难区域，可适当降低地表形变监测精度要求。

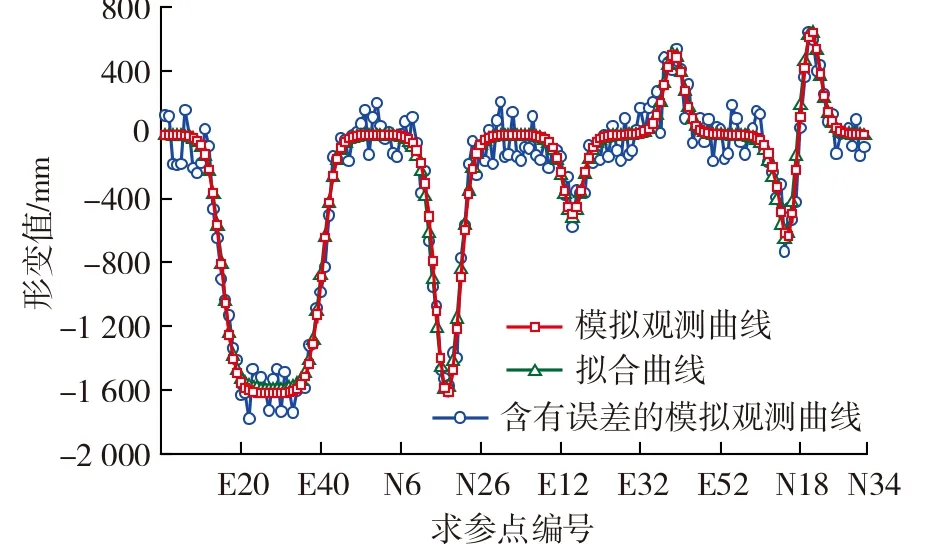
图3 BFWA-MSPP抗差拟合下沉和水平移动效果 Fig. 3 Effect diagram of fitting the subsidence and the horizontal movement by anti-error of BFWA-MSPP

4 工程应用

4.1 矿区概况

以淮南矿区顾桥煤矿1414( 1 )工作面为例，该工作面采用综合机械化采煤，一次采全高，全部垮落法管理顶板。工作面地质采矿条件为：平均采高3 m，工作面倾角5°，平均采深735 m，工作面开采尺寸为2 115.433 m×241.210 m，走向为超充分采动，倾向为非充分采动，总体为非充分采动。地表移动观测站共布设6个控制点和145个监测点，点间距 为30/60 m，倾向观测线长度为1 500 m，走向观测 线长度为3 480 m，工作面和观测线的布设如图4所 示。

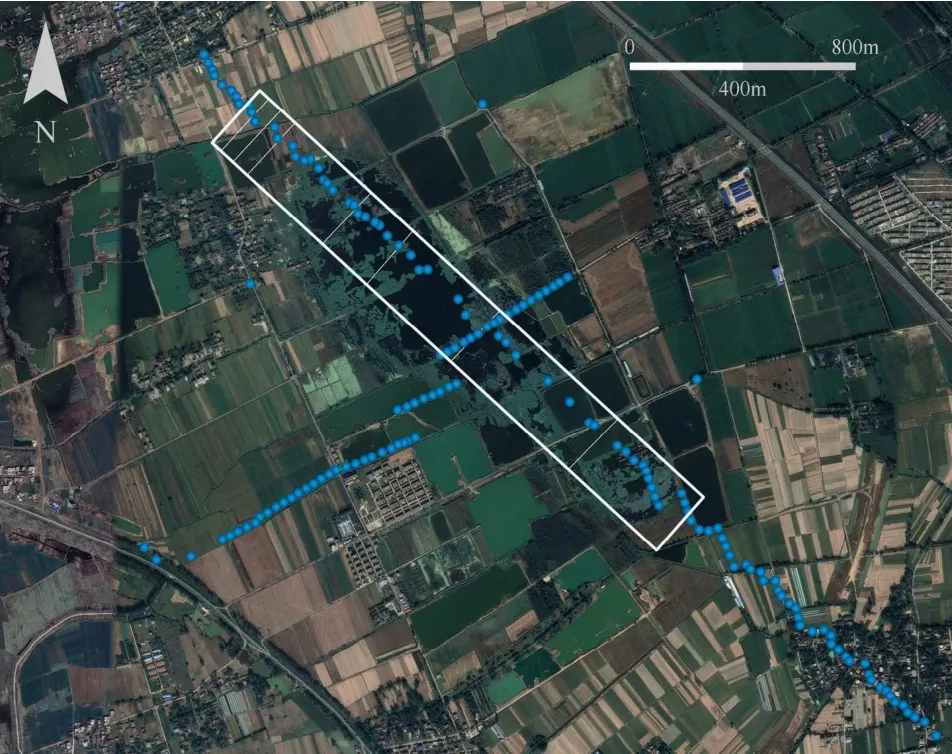
图4 工作面和观测线实地布设 Fig. 4 Field layout of the working face and the observation lines

4.2 试验设计及结果分析

分别利用BFWA-MSPP和PIM-MSPP对1414( 1 )工作面地表移动观测站最后一期观测数据( 地表进入稳定期 )进行开采沉陷预计参数反演，反演结果见表3。

表3 工程应用BFWA-MSPP和PIM-MSPP求参结果比较 Table 3 Comparison between the engineering applications of BFWA-MSPP and PIM-MSPP

从表3中可以看出，2种方法反演参数的差值主要集中在下沉系数q和拐点偏移距S处，就差值所占总体比例来说，下沉系数的差值百分比超过了 10%，拐点偏移距的差值百分比平均约为50%；此 外，开切眼和终采线处的拐点偏移距过大，主要由于工作面走向两侧形成较大砌体梁结构所致。从预计拟合效果来看( 图5 )，无论是曲线边缘部分，还是曲线拐点附近，BFWA-MSPP拟合值更加靠近实测值，2种方法预计拟合下沉和水平移动中误差分别为±83 mm和±108 mm。

5 结 论

( 1 ) 基于Boltzmann函数，融入拐点偏移修正方法，构建了耦合拐点偏移修正的Boltzmann函数预计模型，由于该模型属于高度非线性模型，通过引入FWA，建立了耦合拐点偏移修正的Boltzmann函数模型参数反演方法( BFWA-MSPP )。

图5 BFWA-MSPP和PIM-MSPP预计拟合下沉和水平移动比较 Fig. 5 Comparison of BFWA-MSPP and PIM-MSPP fitting the subsidence and the horizontal movement

( 2 ) 仿真试验结果表明，BFWA-MSPP求参的平均相对误差约为2.1%，平均中误差为2.3，BFWAMSPP预计拟合下沉和水平移动中误差为±6.1 mm。在观测值包含一定的随机误差和粗差后，反演参数的平均相对误差为13.8%，BFWA-MSPP可以有效抵抗观测误差的影响。

( 3 ) 将BFWA-MSPP和PIM-MSPP应用在顾桥 煤矿1414( 1 )工作面，对地表开采稳定后工作面的 开采沉陷预计参数进行了求取，预计拟合下沉和 水平移动中误差分别为±83 mm 和±108 mm；BFWA-MSPP求参结果为：q=1.07，tan β=1.91，b=0.41，θ=88.32°，S1=-18.89 m，S2=14.74 m，S3=48.89 m，S4=64.42 m。