方套圆中空夹层不锈钢管混凝土短柱轴压承载力有限元分析
2021-05-14彭桂瀚宋春生黄国兴
彭桂瀚 宋春生 黄国兴
(1.福州大学土木工程学院 福建福州 350108;2.福州城建设计研究院有限公司 福建福州 350001)
0 引言
钢管混凝土结构受压性能佳且施工方便,可用于拱肋、桥墩与桥塔等结构中。由不锈钢方形外管、碳钢圆形内管及夹层混凝土等组成的方套圆中空夹层不锈钢管混凝土结构具有耐腐蚀性好,对管内混凝土约束效应较普通碳钢管混凝土空心方柱更强等特点[1]。但长期以来由于不锈钢管价格偏高,限制了其在工程中的推广应用,相关研究成果也相应较少。目前试验研究与有限元分析是研究该类结构力学性能的主要手段。
Wang等[2-4]进行了内外圆、矩形、方形等多种截面形式的中空夹层不锈钢管混凝土短柱轴压试验,结果表明承载力规范计算值较试验值偏小;Han等[5]套用碳钢简化公式计算中空夹层不锈钢管混凝土短柱承载力;段振凯[6]、郭建华[7]研究结果表明,约束效应系数、不锈钢类型、空心率及含钢率是影响中空夹层不锈钢管混凝土力学性能的主要因素。目前,缺少不锈钢有关规程指导,如采用碳钢结构公式计算不锈钢结构承载力,或碳钢本构替代不锈钢本构进行模拟计算,均造成计算偏保守[8-10]。
文中以方套圆中空夹层不锈钢管混凝土短柱为研究对象,采用不锈钢Rasmussen本构模型[11],对比Wang[4]试验进行模型验证,并建立基准有限元分析模型,开展空心率、不锈外钢管厚度、混凝土和内钢管强度等结构参数分析,最后提出该类结构承载力修正计算简式,以助于结构的推广与应用。
1 基准有限元模型
通用有限元软件Abaqus建立有限元分析模型,如图1所示。其中钢管采用壳单元S4R模拟外,其他采用实体单元C3D8R。钢管与混凝土模拟为表面接触,不考虑结构初始缺陷与残余应力影响[12]。计算模型底端固定,加载顶端仅竖向可自由变形。
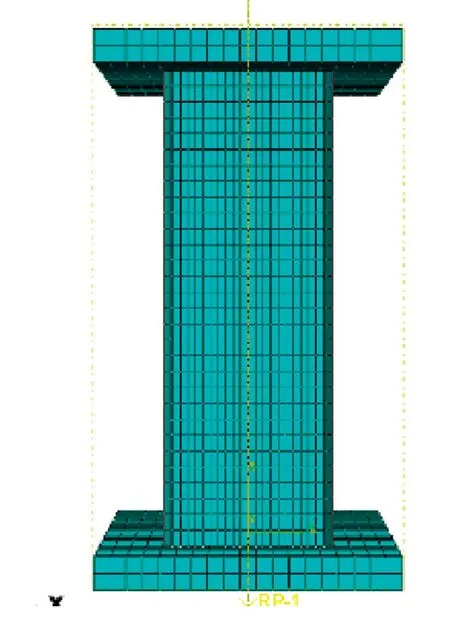
图1 有限元计算模型
碳钢本构模型采用五段式应力-应变关系曲线;内填混凝土本构采用韩林海公式[13];不锈钢外钢管本构采用Rasmussen公式[11],详见式(1)。
(1)
式中,σ0.2与σ0.01分别是残余应变为0.2%、0.01%时的应力;E0为不锈钢弹性模量;n为应变硬化指数;E0.2为不锈钢在应力为σ0.2的切线模量,σu为极限应力,εu为极限应变。
图2示出了QN1803不锈钢拉伸实测曲线与采用Rasmussen公式预测曲线对比图。其中平直段与弯角段曲线最大偏差值分别为6.9%与4.0%。可见,实测与预测应力应变曲线较为吻合。
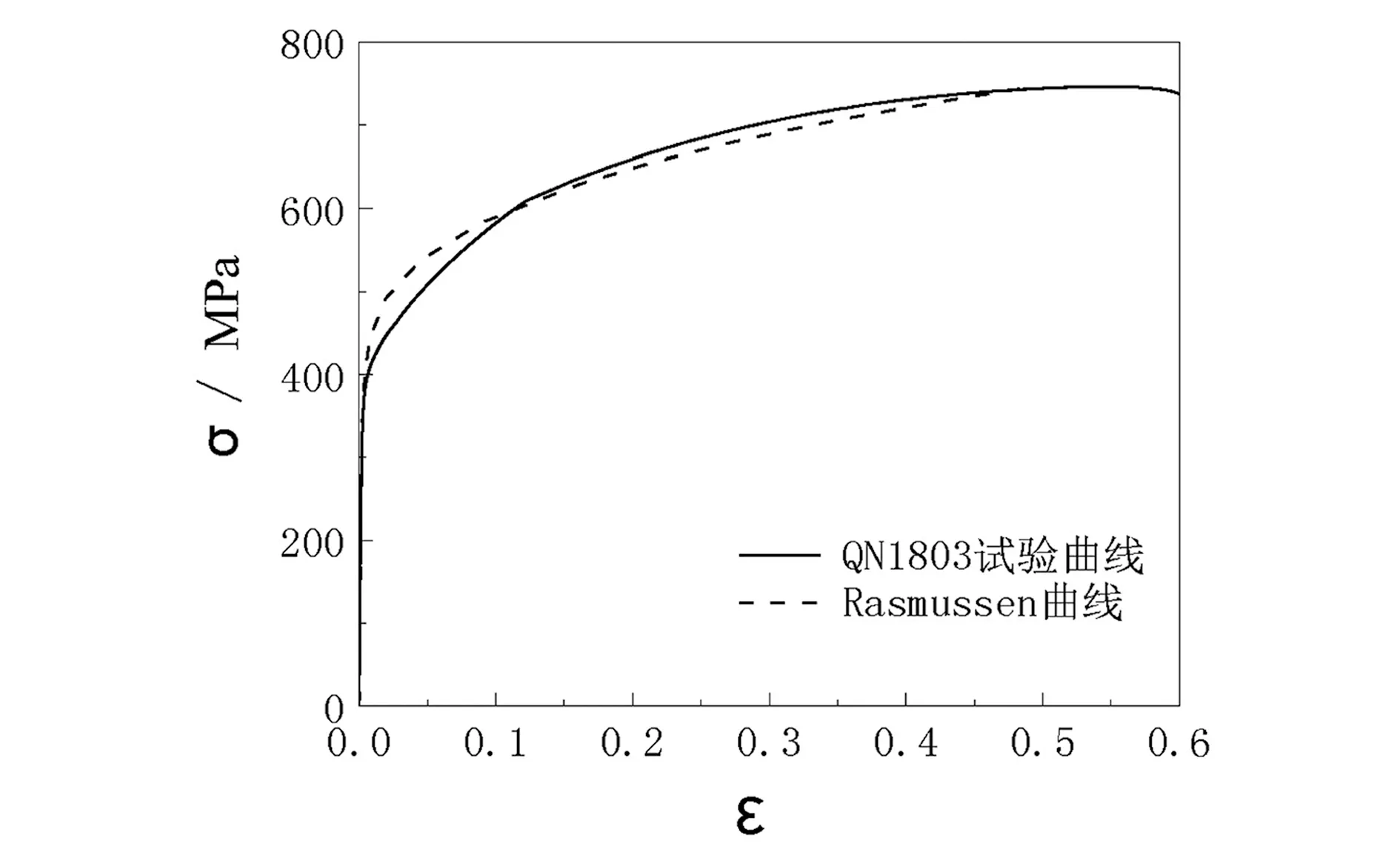
(a)平直段
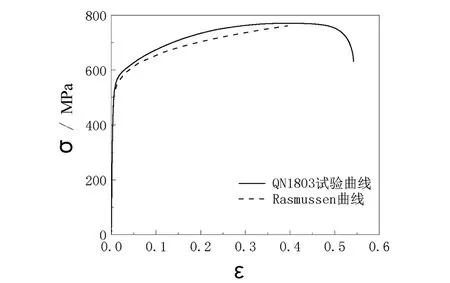
(b)弯角段图2 QN1803不锈钢拉伸试件实测与预测对比

图3 试验装置[4]
文献[4]对19根方中空夹层不锈钢管混凝土轴压短柱进行了试验研究。其中试验装置如图3所示。限于篇幅,图4示出AS150×3-HC22×4,以及试件AS150×3-HC32×6等6根试件试验与有限元分析对比图。可见,曲线反映的荷载-应变发展规律一致。表1列出了AS150×3-HC22×4等9根构件承载力试验值与计算值。其中承载力有限元计算值NFE和试验值Nu比值在0.93~1.05之间,平均值为0.97,标准差为0.04。由此可见,基准有限元模型可较好预测结构承载力,并反应其受力特点。

(a)试件AS150×3-HC22×4
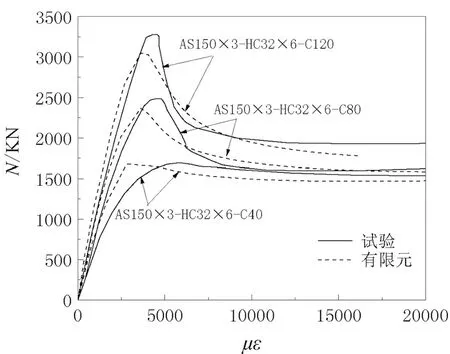
(b)试件AS150×3-HC32×6图4 有限元计算与试验曲线对比[4]
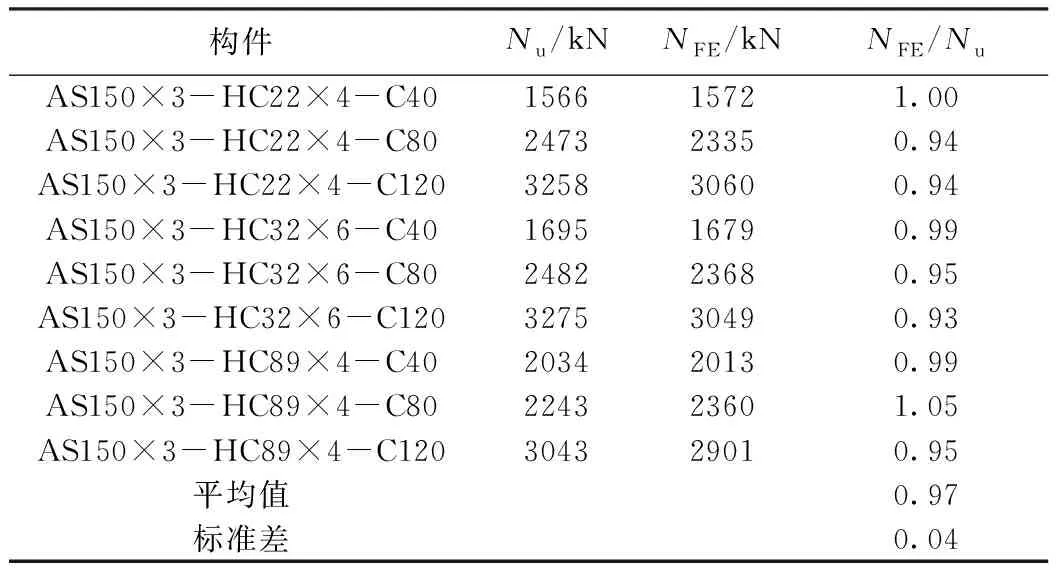
表1 试验构件承载力有限元值和试验值对比
2 承载力参数分析
基于基准有限元模型,开展中空夹层钢管混凝土短柱承载力主要影响参数的分析,包括外钢管厚度、内钢管强度、混凝土强度、空心率等。各结构参数对荷载-应变曲线与承载力影响如图5~图8所示。

(a)荷载-位移曲线
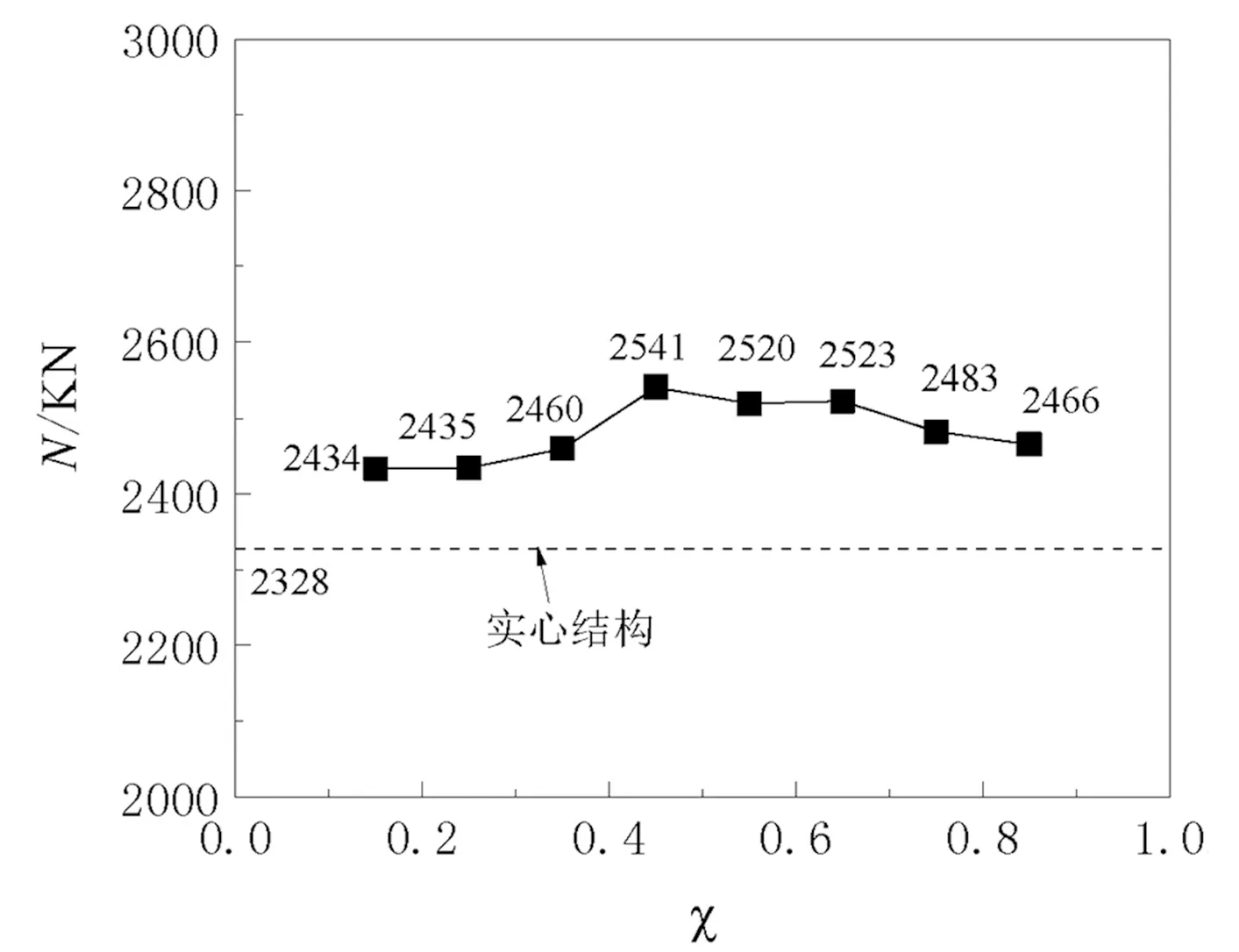
(b)极限承载力图5 空心率影响
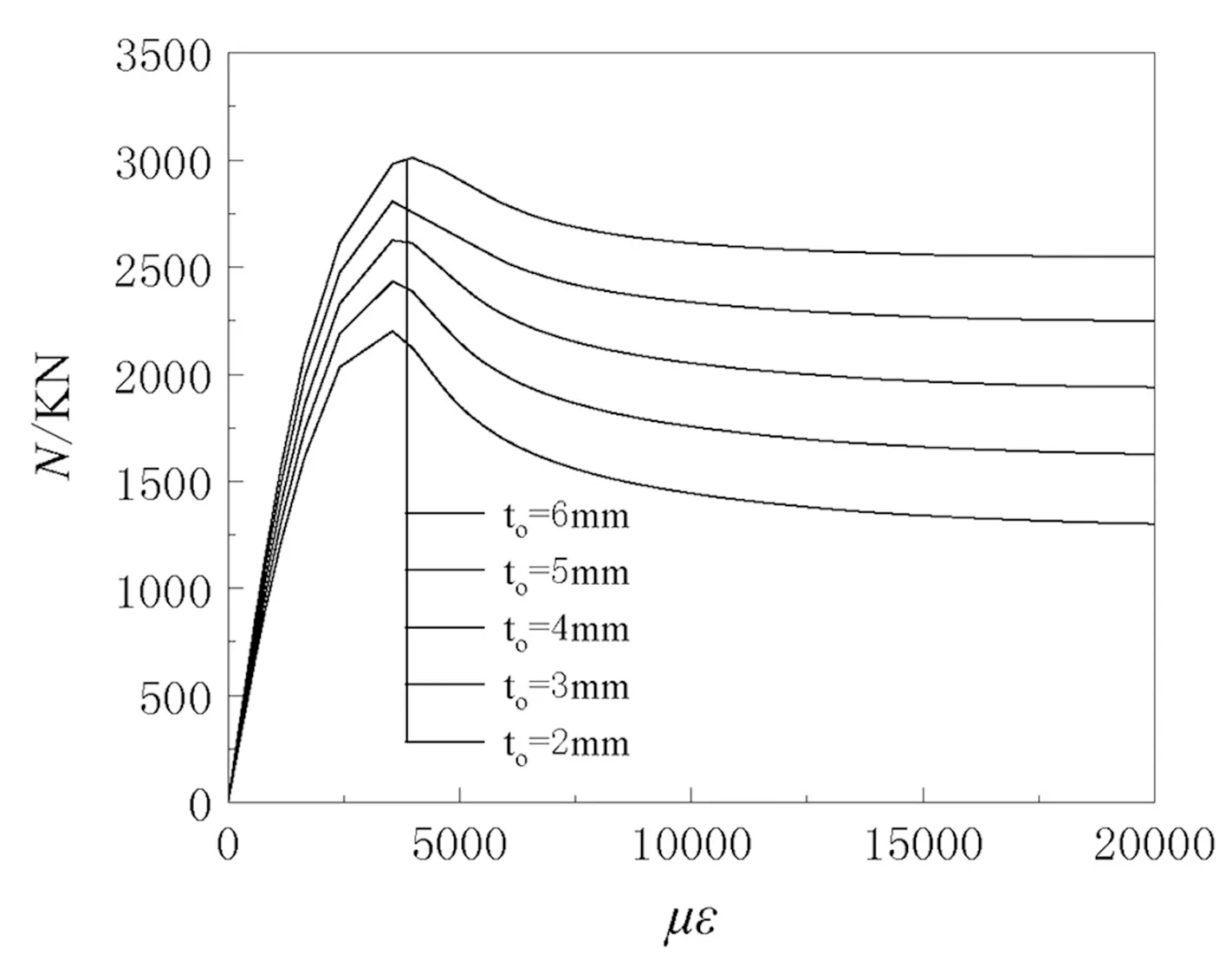
(a)荷载-位移曲线
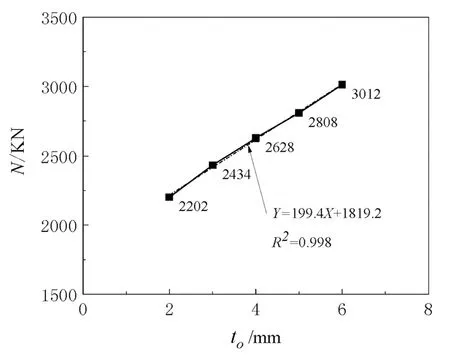
(b)极限承载力图6 外钢管壁厚影响
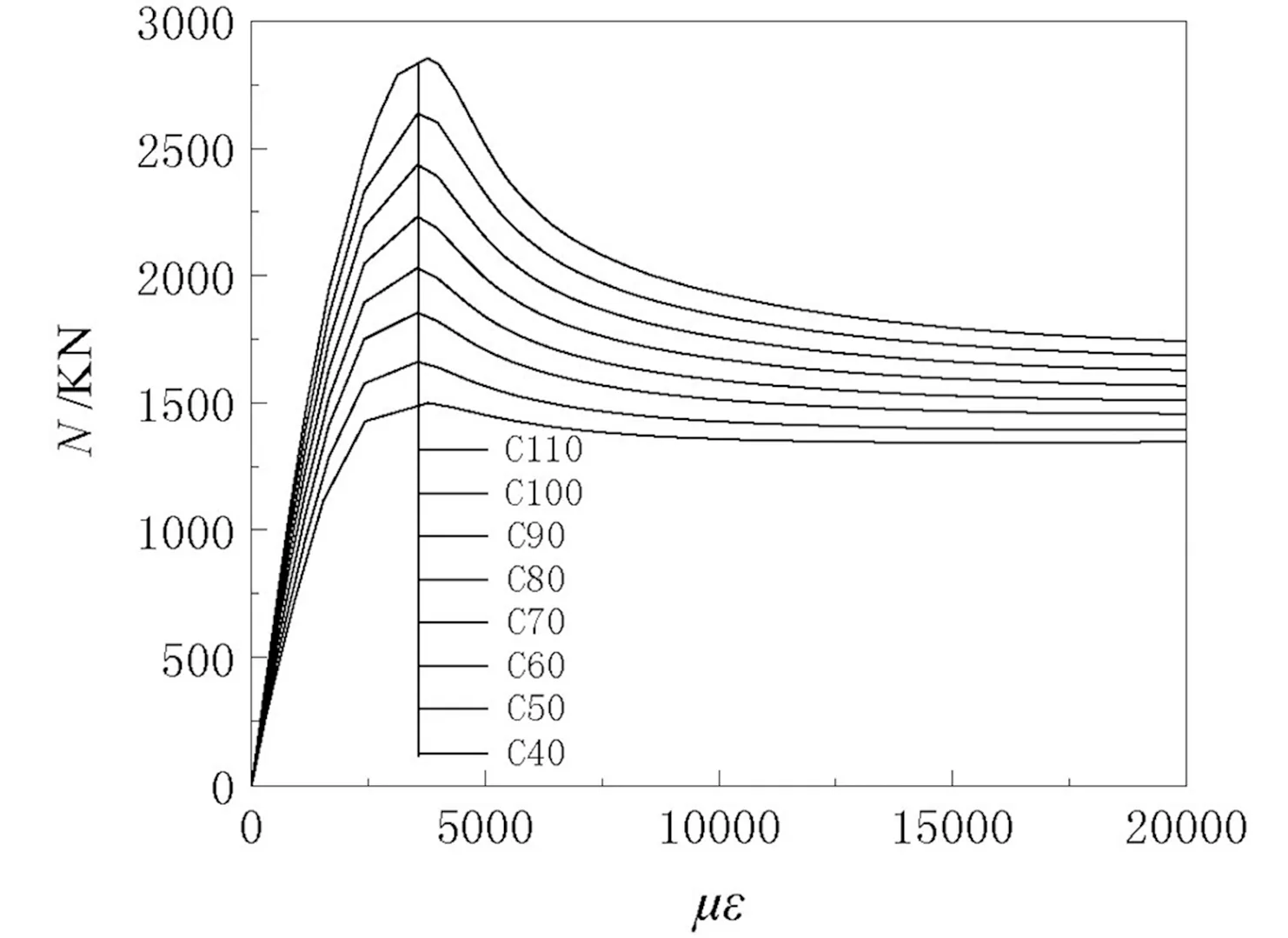
(a)荷载-位移曲线
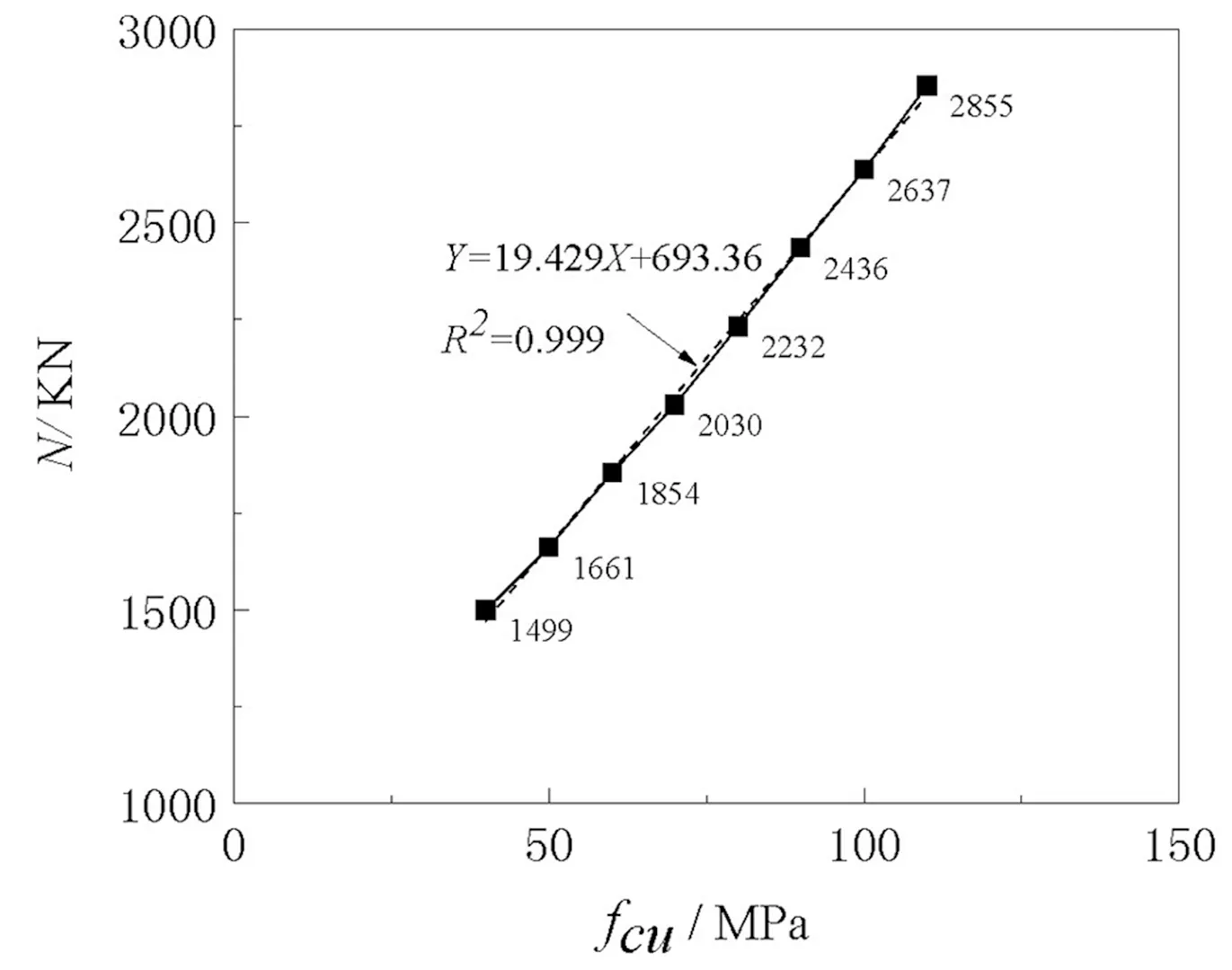
(b)极限承载力图7 混凝土强度影响
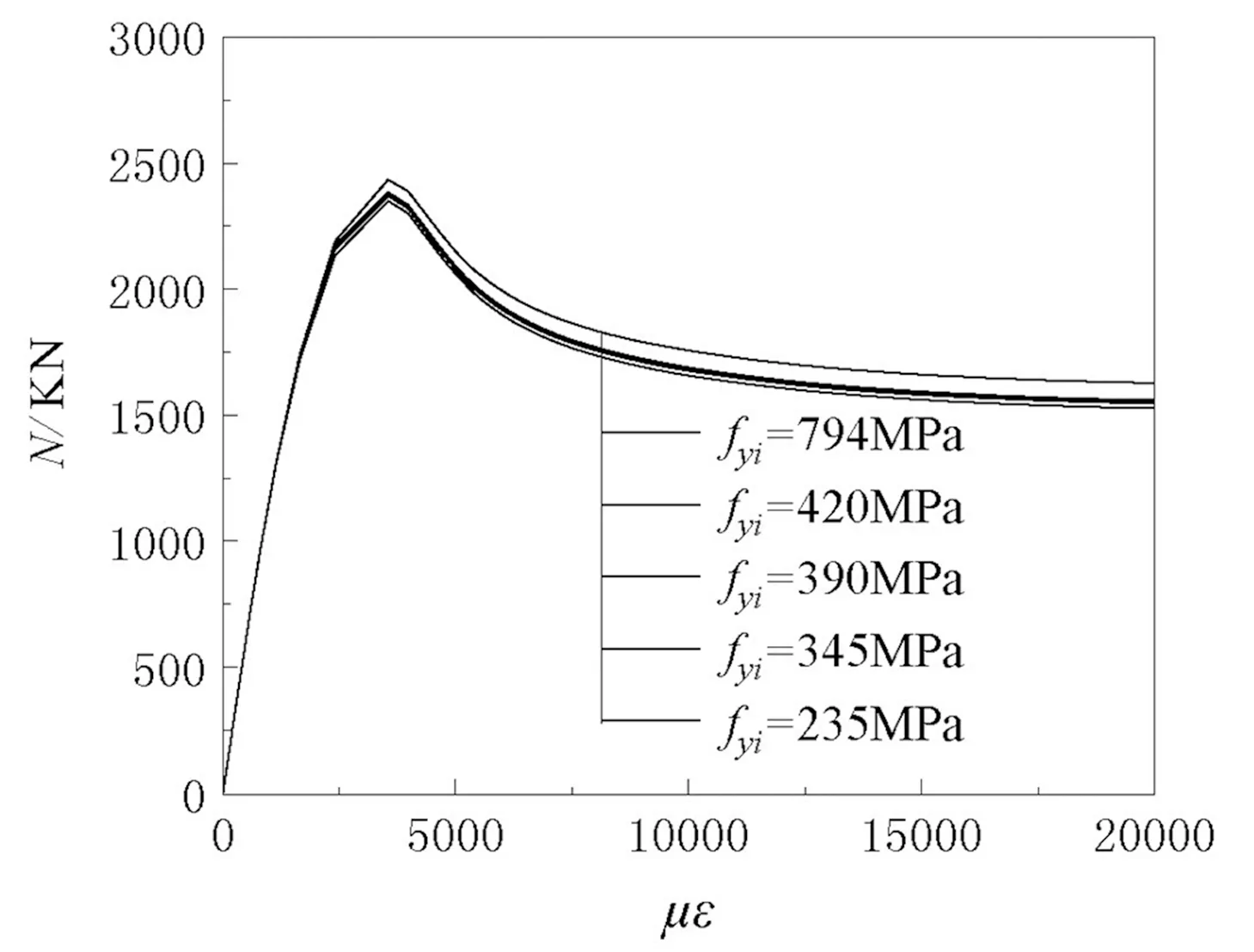
(a)荷载-位移曲线
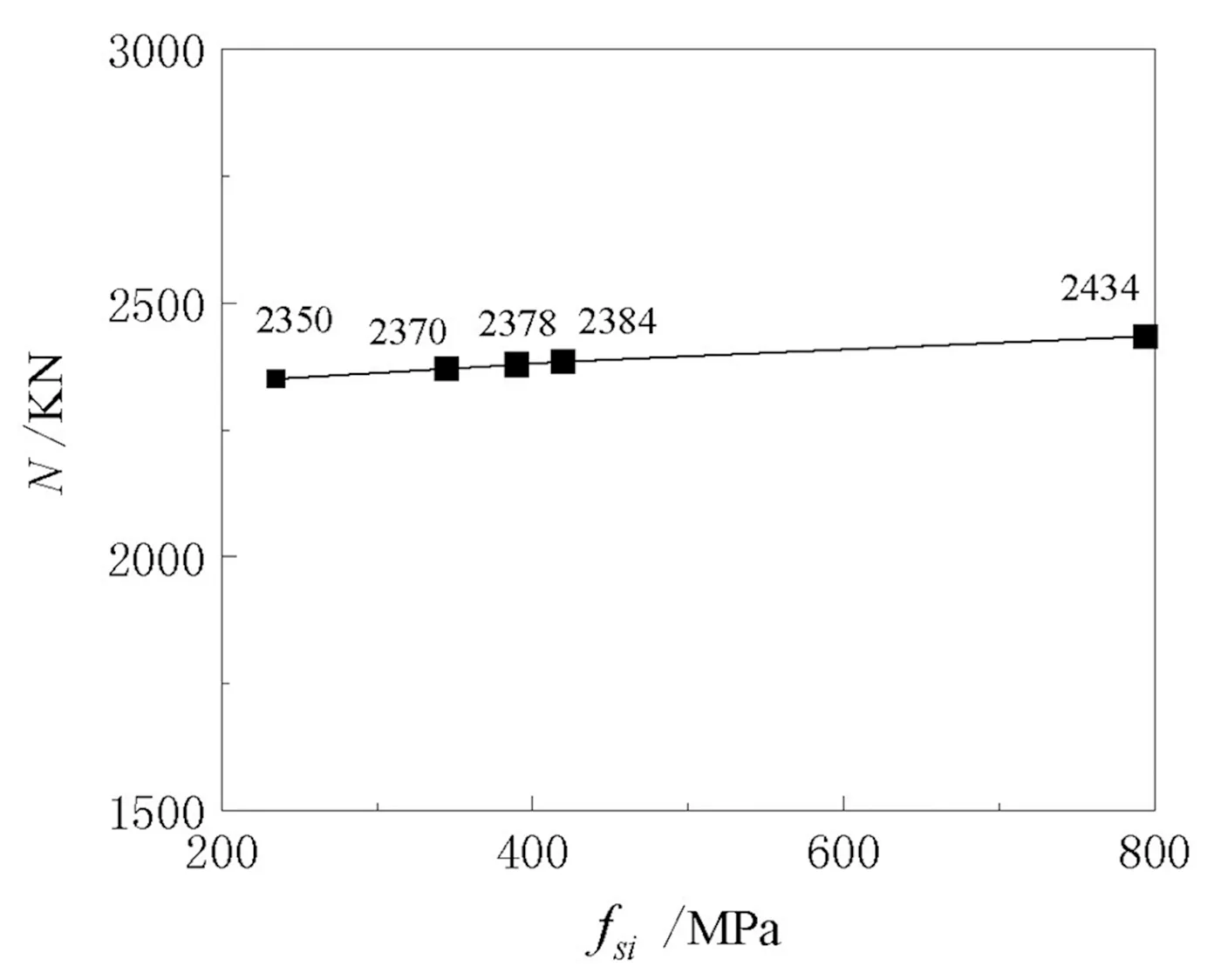
(b)极限承载力图8 内钢管强度影响
空心率增大,内钢管面积与含钢率随之加大,荷载-应变曲线峰值相差不大,但峰值后下降段斜率变小,结构表现出更优的延性,如图5(a)所示。采用高强内钢管(屈服强度794MPa),结构承载力将随空心率增大先增后减,空心率0.45时达到最大承载力2541kN,均大于实心方管承载力2328kN,增幅4.6%~9.2%,如图5(b)所示。可见,中空夹层结构可通过提高内钢管强度以弥补空心率加大,夹层混凝土面积减少而造成的承载力降低[14]。
不锈外钢管壁厚大小决定了结构含钢量。壁厚加大在增加含钢量的同时,也提高了结构初始刚度及结构承载力。如图6(b)所示,承载力与外钢管壁厚呈线性正比关系,壁厚增加200%,含钢率增加223%,极限承载力可提高36.8%。但壁厚对于峰值后应变下降率即后期结构影响不大如图6(a)所示。
混凝土强度对于承载力影响类似于壁厚,强度增加175%,承载力线性提高90.5%。混凝土强度提高降低了外钢管约束效应,荷载-应变曲线表现为峰值后下降段斜率有所增大,结构脆性增加,延性下降如图7所示。
图8示出了内钢管强度对结构受力影响。可见,在空心率定值时,内钢管强度对于结构承载力贡献有限,提高238%,承载力仅增大3.6%;同时对于后期延性、峰值应变及初始刚度等无明显影响。
3 承载力修正计算简式
如采用基于碳钢的简化公式计算方套圆中空夹层不锈钢钢管混凝土短柱极限承载力过于保守[5]。拓展约束效应系数和空心率参数,提出适用承载力修正计算简式,如式(2)所示。
Nu=K·[(Aso+Ac)fscy+Asifyi]
(2)
K=K1χ2+K2χ+K3ξ+K4
(3)
(4)
式中,Aso、Asi和Ac分别为外钢管、内钢管和混凝土的截面面积;fscy为不锈钢外管与内填混凝土的组合轴压强度[5];fyi为内钢管的屈服强度。K为强度提高系数,与空心率和约束效应系数有关,如式(3);χ为空心率;ξ为约束效应系数,按式(4)计算;K1-K4为计算系数,基于45个有限元模型参数分析结果,先后拟合空心率与提高系数K、约束效应系数与空心率关系后,得K1=0.31;K2=-0.36;K3=-0.16;K4=1.38。
修正计算简式2对文献[4]的12根方中空夹层不锈钢管混凝土轴压短柱进行试算,并与试验值进行对比,列于表2与图9。可见,计算值与试验值吻合较好,两者平均值比值为1.01,标准差为0.04。因此,研究参数范围内,提出的修正计算简式可较为准确预测方套圆中空夹层不锈钢管混凝土轴压短柱的极限承载力。

表2 修正公式计算值与试验值对比
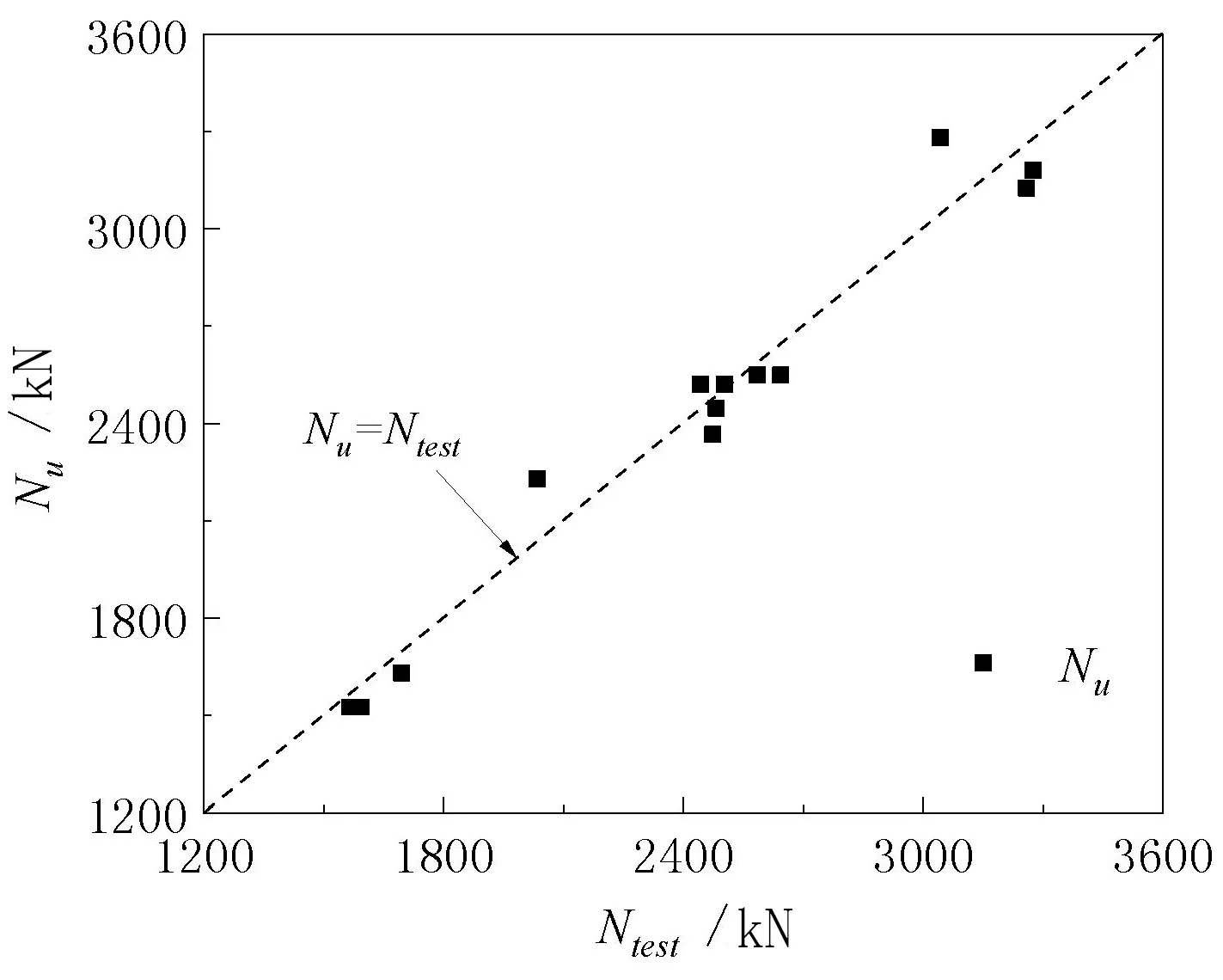
图9 极限承载力修正计算值与试验值[4]比较
4 结论
本文基于试验验证,建立了基准有限元分析模型,开展了方套圆中空夹层不锈钢管混凝土轴压短柱参数分析,得到以下结论:
(1)不锈钢采用Rasmussen本构关系的有限元分析模型可较准确计算方套圆中空夹层不锈钢管混凝土短柱结构承载力。
(2)研究参数范围内,不锈外钢管壁厚、内填混凝土强度与结构承载力呈线性正比关系;内钢管强度对结构承载力影响较小;采用高强内钢管时,承载力随空心率加大先增后减,变化幅值不大;当空心率0.45时承载力最大,但均大于实心结构承载力。
(3)提出的方套圆中空夹层不锈钢管混凝土轴压短柱极限承载力修正简式适用于该类结构,可预测承载力。
