计及综合需求侧响应的能源枢纽多目标运行优化方法
2021-05-14黄旭锐苏亚纳侯宏娟朱以顺
黄旭锐,苏亚纳,侯宏娟,3,杨 波,潘 军,朱以顺
(1.广东电网有限责任公司广州供电局,广东 广州 510600;2.华北电力大学能源动力与机械工程学院,北京 102206;3.华北电力大学新能源电力系统国家重点实验室,北京 102206)
综合需求侧响应(integrated demand response,IDR)参与的能源枢纽系统在构建综合评价指标,因目标点可行域非凸,在确定权重方面存在难点。而目标的确定,是进行能源枢纽系统优化的前提。
目前对于能源枢纽系统优化的单目标模型中,通常在考虑IDR前提下从能效[1]或收益[2-3]方面进行优化研究。但在多目标模型中,由于各个目标之间可能存在冲突,通常并不能得到使得每个指标都达到绝对最优解。因此,更多的研究探索通过运用一些数学方法求得折衷解。文献[4-5]采用模糊满足技术选择最佳折衷方案。文献[6]将主观与客观赋权法结合,提出层次分析-熵权赋权法,从经济、能耗、环境3方面构建评价指标。一些学者采用帕累托优化方法处理多目标优化问题:文献[7]利用处理多目标凸优化问题的标量化方法求解帕累托前沿(PF),将多目标优化问题处理成凸优化问题简化了问题求解;此外,也有文献利用智能算法进行多目标寻优,采用遗传算法[8-9]、粒子群优化算法[10]、进化算法[11-12]等算法,优化产生综合能源系统最优配置方案的帕累托前沿,通过决策者所考虑的目标价值、偏好等策略选择合适的方案。但该类多目标能源枢纽优化研究并未考虑到IDR参与的系统优化问题。
对于未计及综合需求侧响应的能源枢纽高效、经济等多目标运行优化问题,可以通过分析权重确定综合指标。而对于计及综合需求侧响应的能源枢纽系统评价指标的建立方法,目前该类研究较少。因为综合需求侧响应是通过预测需求侧弹性负荷确定理想负荷分配/理想运行调度方案,进而调整价格引导用户改变用能方式,但当以能耗、收益作为子目标时,计算模型非凸,也就是说博弈均衡后的能耗收益数据点在坐标系中的可行域非凸,进而难以确定多目标权重。
为了使计及综合需求侧响应的能源枢纽系统供需博弈均衡点可行域为凸集,进而简化多目标运行优化方案的求解,本文采用“成本”替换“收益”作为子目标。由于成本只反映系统运行时的实际成本并不受供需博弈过程中价格的影响,从而可将供需博弈后的均衡点看成尽可能贴合能源枢纽理想负荷分配,将计及综合需求侧响应的能源枢纽多目标运行优化问题简化为如何确定多目标需求下的理想负荷分配的问题。
综上所述,本文对计及综合需求侧响应的能源枢纽系统,基于日前多目标优化问题,进行如下研究工作:1)建立能源枢纽各设备数学模型,以及分目标数学模型;2)建立综合需求侧响应数学模型;3)基于用户侧负荷需求,通过标量化方法进行能源枢纽系统多目标权重分析并确定理想点,进而以目标向量点与理想点归一化后的欧氏距离建立目标函数;4)以负荷分配为粒子,以在特定权重下能源枢纽运行的目标函数值为适应度函数,通过粒子群优化算法确定能源枢纽多目标需求下的理想负荷分配。
1 能源枢纽数学模型
能源枢纽基本架构(图1)包括蓄电、蓄冷、蓄热设备,电热泵(制热),电热泵(制冷),冷热电联供(combined cooling heating and power,CCHP)设备等能量转化设备。能源枢纽一次侧能源供应包括电网、市政燃气、风能和太阳能,二次侧(需求侧)包括电负荷、热负荷和冷负荷3种类型。

图1 能源枢纽基本架构Fig.1 Basic structure of the energy hub
1.1 冷热电联供系统约束
CCHP系统在最大出力和爬坡约束的前提下,还应满足在不同负荷率下的能量转换关系:
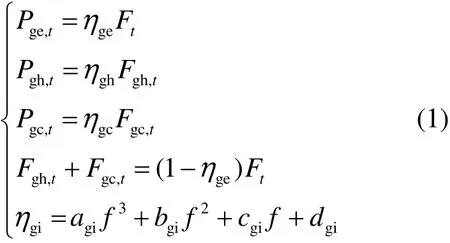
式中:t为时间节点;P为出力(其中冷/热出力在计算上均以㶲来表示);gi表示CCHP出力类型,gi即ge、gh、gc,分别代表CCHP供电、供热、供冷;F为天然气燃烧转化的有用能;ηgi为CCHP的gi种出力的㶲效率;f为负荷率;agi、bgi、cgi、dgi为gi种用能方式中㶲效率与负荷率关系的相关方程系数。
1.2 储能设备约束
储能设备约束包括对电储、热储、冷储设备的充放约束、存储状态约束与调度周期的充放平衡约束,同时储能设备应考虑存储容量与充放系数的关系。文献[7]采用2个独立变量表达储能充放行为,并分析了系统在优化过程中避免了储能设备同时充放行为造成的额外能耗、成本、污染物排放量,所以本文将储能的充放行为简化为1个变量,其表达式为

式中:Psi,t,min、Psi,t、Psi,t,max分别代表t时刻储能设备si的充/放出力(正数为放,负数为充)以及出力的上下限;si(se、sh、sc)为储能设备类型,分别代表蓄电、蓄热、蓄冷;S为储能设备㶲存储量;ηsi,in、ηsi,out、fsi分别代表储能设备si的充/放系数以及储能设备存储率;asi,in、bsi,in、csi,in、dsi,in、asi,out、bsi,out、csi,out、dsi,out代表储能设备si的充放系数与设备存储率关系的相关方程系数。
1.3 风电、光热设备约束条件
鉴于系统存在弃风、弃光的可能性,对风电、光热出力约束为

式中:下标w、s分别代表风电和光热设备;Pt,max为t时刻天气因素下的设备出力预测值
1.4 电制热、电制冷设备约束
建立电制热、电制冷设备线性数学模型,其约束为

式中:下标pi=ph,pc分别代表电制热、电制冷设备;ηpi、fpi分别代表pi设备能源转化效率、负荷率;api、bpi、cpi、dpi代表pi设备能源转化效率与负荷率关系的相关方程系数;Leph、Lepc分别代表电制热、电制冷设备消耗的区域电网电量。
1.5 供需平衡约束
假设用户侧24 h负荷需求为L,t时刻负荷需求为Lt,t时刻的运行调度方案为Mt,表达式为
Mt需满足的供需平衡方程如下:
式中:Pc代表市电购电量;下标egrid、hgrid、cgrid分别代表IES的电、热、冷网。
1.6 子目标数学模型
1.6.1 能耗数学模型
单耗分析理论是基于㶲分析和㶲经济学分析的基础上发展起来的能量系统分析方法[13-14]。本文基于单耗分析理论建立了系统能耗方程:
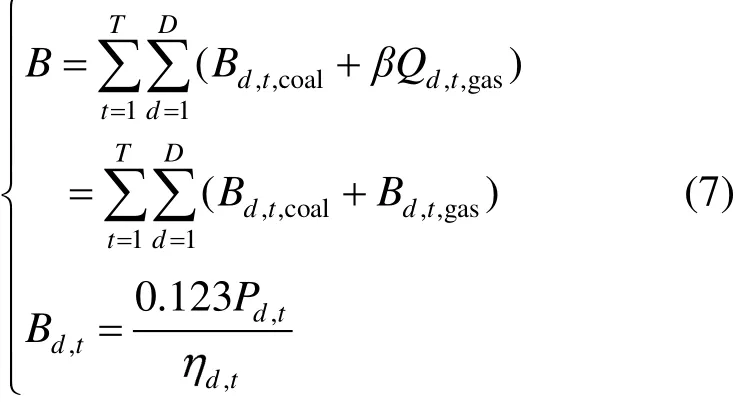
式中:B为总燃料消耗量;t为时间,t=1,2,3,…,T,T为总时间;d为设备编码,d=1,2,3,…,D,D为设备总数;Bd,t,coal、Qd,t,gas、Bd,t,gas分别表示t时设备d的煤耗(包括外网购电对应的供电煤耗)、天然气消耗量以及折算后的煤耗;β为天然气-标准煤折算比,β=Cgas/Ccoal(其中Cgas、Ccoal分别为天然气、标准煤的能值);Pd,t为t时d设备出力;ηd,t为t时d设备的㶲效率。
1.6.2 成本数学模型
在IES的调度运行问题中,设备运行成本是成本目标函数的主要组成部分,主要包括IES的外电网购电成本、购气成本以及系统运维成本。

式中:C为运行调度总成本;pd,t,egrid为t时外电网购电价格;Pc,d,t,egrid为t时d设备市网购电量;pd,t,gas为t时天然气购气价格;Qd,t,gas为t时d设备天然气购气量;Cd,t,run为t时d设备运维成本。
2 综合需求侧响应数学模型
在综合需求侧响应中,多种负荷都有相应的需求价格弹性。需求价格弹性表示各时段某类负荷对其价格的灵敏度,即在一定时段内负荷变化率与该类负荷价格变化率之比:

式中:ek,ii为i时段k类负荷用量随该时段价格的变化情况,即该时段的自弹性;ek,ij为k类负荷i时段的负荷用量随j时段价格的变化情况,即j对i时刻的交叉弹性;Lk,i0和pk,i0分别为i时段的k类负荷原始用量和原始价格;Lk,i和pk,i分别为实行分时价格后i时段的k类负荷用量和分时价格;
对于k类负荷而言,由自弹性和交叉弹性组成的弹性矩阵Ek为

式中,n为时段数,如对于单日运行调度问题通常n取24。主对角线元素为自弹性,通常该值为负;非对角线元素为交叉弹性,通常该值为正。
3 能源枢纽运行优化方法
3.1 多目标权重分析
能源枢纽通常以单日负荷需求,进行运行优化。而对于单日多目标运行优化问题,常采用标量化方法,遍历权值求解帕累托前沿,最后通过某种策略进行最优解选择。
本文基于用户侧负荷需求,采用标量化方法过遍历权值求取帕累托非劣解集合R,R∈帕累托前沿,表达式为
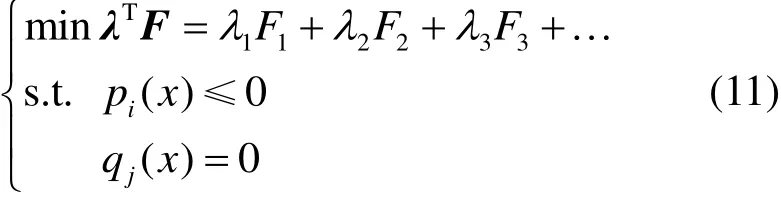
式中:λ为权向量;i为不等式约束条件编码,i=1, 2,3, …;j为等式约束条件编码,j=1, 2, 3, …。
采用理想点法,以目标向量点与理想点归一化后的欧氏距离作为目标函数,表达式为
式中:M为n个小时运行调度方案,M=[M1,M2,M3, …,Mn];N为目标个数;Fi、分别为第i个目标函数原始值、归一化后的目标值;Fi,min为第i个目标最小值。通过公式(11)选取R中最优解,进而确定多目标权重。
3.2 理想负荷分配求解
对于综合需求侧响应参与下的能源枢纽系统而言,供需博弈行为意味着博弈平衡时的多目标在某种策略下优于无综合需求侧响应参与下的系统运行结果。而本文所建立的分目标在供需博弈过程中与博弈过程中的价格无直接数量关系,从而可将供需博弈后的均衡点看成尽可能贴合能源枢纽理想负荷分配,将计及综合需求侧响应的能源枢纽多目标运行优化问题简化为如何确定多目标需求下的理想负荷分配的问题。
目前并无保证所求理想负荷配全局最优的有效方法,为此本文采用一种局部最优的优化方法,即以负荷分配为粒子,以在3.1节特定权重下能源枢纽运行的目标函数为适应度函数,通过粒子群优化算法确定能源枢纽多目标需求下的理想负荷分配。
4 案例分析
以广州夏至日某工业园区冷热电负荷需求为例进行分析。日前,该工业园区24 h电、热、冷负荷需求如图2所示,其中,热、冷负荷均是㶲负荷。由图2可见:电负荷占最大比重,其主要用于工业生产与办公;热负荷主要用于园区的生活热水和部分厂房生产用热;冷负荷用于中央空调系统和部分厂房新风系统。夏至日均温取31 ℃,热网供水温度55 ℃,冷网供水温度7 ℃。假设各原始时刻电、热、冷弹性负荷占比均为10%,均为可转移负荷。

图2 24 h电、热、冷负荷Fig.2 The 24-hour electrical, heating and cooling load
以风电、光热、CCHP、储能设备搭建的能源枢纽系统为研究对象,分析在计及综合需求侧响应参与下的能源枢纽系统日前多目标运行优化调度方案。市电电价为0.5元/(kW·h);天然气热值取35 564 kJ/m3,标准煤热值取29 288 kJ/kg;1 m3天然气相当于1.21 kg标准煤,天然气价格取3.45元/m3;蓄电池最大容量为1 MW,蓄热罐最大容量为0.3 MW,蓄冷罐最大容量为0.3 MW。电热泵制热时满负荷能值系数取0.76,制冷时满负荷能质系数取0.61。各污染物排放系数取值参考文献[15]。CCHP设备最大发电量取15.6 MW,最大制热㶲量取2.23 MW,最大制冷㶲量取2.23 MW;电热泵最大热㶲出力取1.6 MW,最大冷㶲出力取1.2 MW;其他涉及到计算燃料消耗量的相关系数参照表1。

表1 案例相关系数Tab.1 Related coefficients of the case
4.1 不考虑综合需求侧响应的能源枢纽系统多目标运行调度结果
基于图2所示的原始负荷需求,根据3.1节计算不考虑综合需求侧响应时的能源枢纽系统多目标运行调度结果。
其中标量化方法的步长取0.001。求解的双目标问题的帕累托前沿如图3所示。图3中,红色数据点为帕累托非劣解,蓝色点(207 845, 441 123)为理想点,绿色点(212 021, 445 416)对应的公式(11)目标函数值最小点,该绿色点所对应的权向量为(0.205, 0.795)T。
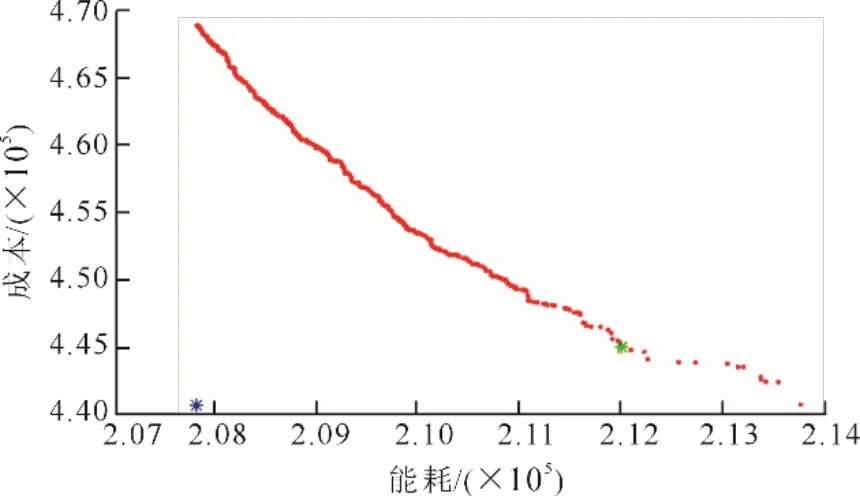
图3 双目标问题的帕累托前沿Fig.3 The Pareto fronts of two-objective problem
4.2 计及弹性负荷的能源枢纽系统多目标理想负荷分配
基于图2所示的原始负荷需求,已知原始时刻电、热、冷弹性负荷占比为10%。采用粒子群算法,以负荷分配为粒子(每一粒子各时刻运行方式均采用加权和单目标优化方法,权向量为4.1节求得的(0.205, 0.795)T),以公式(11)所建立的目标函数为适应度函数,其中粒子数为50,迭代周期为100。理想负荷分配及各时刻负荷调节量如图4所示。

图4 理想负荷分配及各时刻负荷调节量Fig.4 The ideal load-distribution and load regulations at each time
由图4可以看出,理想负荷分配的峰谷趋势相比于原负荷的峰谷更加平缓,这表明调整负荷分配有利于能源枢纽缓解高峰负荷需求,可以达到移峰平谷的作用。
另外,理想负荷分配对应的运行调度能耗成本点为(210 412, 443 426)。对比4.1与该结果目标函数值,经计算相比于4.1节的运行调度结果,该结果的目标函数值减小了39.9%。可见,在建立的多目标目标函数基础上,调整负荷分配有利于能源枢纽对运行调度进行深度优化。
4.3 计及综合需求侧响应的能源枢纽系统供需博弈均衡时的运行调度结果
假设用户侧电、热、冷负荷需求均由能源枢纽满足,且用户随能源枢纽的价格波动,积极调节负荷需求。假设3种负荷初始价格均取0.5元/(kW·h);交叉弹性数值均取1 000,自弹性数值均取0。供需博弈中,用户侧以最小用能费用为目标,以前次负荷需求向量为初值,在0.9~1.1倍初始负荷需求向量间通过非线性寻优方法求解新的负荷需求向量;能源枢纽以尽可能贴近理想负荷分配为目标,同时考虑固定权向量下的结果有被支配解的可能,在一定范围内微调权向量;加入过往博弈记忆分析模块,若当前博弈结果劣于前者,及时纠偏。实际负荷需求与理想负荷分配的偏差用D表示,表达式为

式中:Lk,t表示博弈过程中用户侧t时刻k类负荷需求量;Lideal,k,t表示理想负荷分配中t时刻k类负荷理想值。
计及综合需求侧响应的能源枢纽与用户侧的供需博弈过程如图5a)所示,红色点为每一次博弈后的偏差D-用户侧用能成本点,随着博弈次数的增加到50次之后出现了往复现象,最终均衡于蓝色“*”点,即用户侧由初始负荷需求调整为均衡点时的负荷需求;图5b)表示博弈过程中每次博弈的负荷分配所对应的目标函数值。而图6为博弈均衡时各负荷24 h价格。该价格相比于初始价格调节趋势,与图4理想负荷分配的各时刻负荷调节方向相反,以达到激励用户调节自身负荷需求贴近能源枢纽理想负荷分配的目的。

图5 供需博弈过程Fig.5 The game progress of supply side and demand side

图6 均衡点各负荷价格Fig.6 The price at each load at the balance point
另外,供需博弈均衡时的负荷分配所对应的能源枢纽能耗-成本点为(210 133,446 935),相比于4.2节的运行调度结果,虽然该结果的目标函数值增加了16.8%,但相比于4.1节的运行调度结果,该结果的目标函数值减小了23.1%。
可见,基于综合需求侧响应,能源枢纽应用价格激励措施引导用户侧改变用能方式。随着供需博弈过程逐渐贴近理想负荷分配,优化结果逐渐良好。即使达不到完全贴合理想负荷分配的要求,但贴近程度越高(偏差D越小),得到的优化结果也越好。
5 结 论
本文基于计及综合需求侧响应的能源枢纽日前多目标优化问题,提出一种局部最优的多目标优化方法。建立了能耗、成本子目标函数,分2阶段进行优化:1)基于用户侧初始负荷需求,通过标量化方法进行能源枢纽系统多目标权重分析并确定理想点,进而以目标向量点与理想点归一化后的欧氏距离建立目标函数;2)以负荷分配为粒子,以在特定权重下能源枢纽运行的目标函数值为适应度函数,通过粒子群优化算法确定能源枢纽多目标需求下的理想负荷分配。
通过实例验证,计及综合需求侧响应,合理地调整负荷分配能有效降低能源枢纽期望的目标函数值,而供需博弈过程中的负荷分配贴近理想负荷分配的程度越高,运行优化结果越良好。
