大型桥梁施工风险动态评估
2021-05-14余万庆韦庆冬
施 洲,纪 锋,余万庆,韦庆冬
(1. 西南交通大学土木工程学院,四川成都610031;2. 中国铁路上海局集团有限公司南京铁路枢纽工程建设指挥部,江苏南京200142)
随着我国高速铁路、公路的不断发展,千米级以上跨径大、结构新的桥梁不断兴建,在此类大型桥梁的施工过程中,风险因素也随之增多。桥梁施工中的风险因素不仅数量众多而且具有前后关联的特点,致使桥梁工程施工安全面临极大挑战。为科学控制桥梁施工风险,国内外学者采用事故统计法、专家调查法、故障树理论、WBS‒RBS(工作分解‒风险分解)及层次分析法[1]等开展风险识别与评估研究。Hashemi 等[2]采用一种混合问卷调查和置信区间的方法计算桥梁施工过程中的风险事件概率和损失值。Gholamreza 等[3]采用故障树和事件树方法构建评估模型,并对桥梁施工过程中风险事件与风险因素之间的影响关系进行评估。Chen等[4]通过贝叶斯网络建立了桥梁建设项目安全风险评估模型,分析安全风险因素之间的影响关系。Ahn 等[5]分析了桥梁建设中的风险因素,并采用多元回归分析建立风险损失估计模型,开展桥梁风险损失分析。阮欣等[6]针对现阶段国内外大型桥梁工程风险问题,初步建立了桥梁风险评估体系。陆新鑫等[7]基于肯特指数法,在分析桥梁施工事故原因的基础上,建立评估模型。刘沐宇等[8]采用集对分析理论,建立了基于多元联系数的桥梁施工风险评价模型。赵延龙[9]运用贝叶斯定理建立大跨径斜拉桥上部结构施工安全风险评估模型,系统分析了桥梁施工风险。上述方法以施工各工序中的风险源事件为核心,建立风险事件‒因素之间分层评估模型并评估出风险等级,提出针对性控制措施,实现了桥梁工程风险静态评估与控制。
在实际桥梁施工过程中,风险事件是相互影响的,在大跨径或复杂结构桥梁工程中,风险事件发生往往是一系列相继触发的连锁传递过程,使桥梁工程施工风险呈现出随时间推移的动态传递特征。针对风险事件传递的研究,李存斌[10]提出了风险元概念,并阐述了工程项目中风险元传递基本理论。孟祥坤等[11]基于风险熵和复杂网络分析了深水钻井井喷事故风险因素之间的演化过程。在桥梁工程项目中,康俊涛等[12]提出一种基于贝叶斯网络理论的安全性评价方法,并应用于一座斜拉桥上部结构施工过程,通过形成事故链分析了风险因素与风险事件之间的传递网络,从中成功评估出安全风险的传递主路径。Mortazavi 等[13]等基于风险的动态传递特性,采用调查表法获取风险因素之间的因果关系,并结合系统动力学建模分析风险传递特性。温欣岚等[14]将链式风险评估方法和静态风险评估方法进行对比研究,发现链式风险评估方法尽管计算量大、评估繁杂,但评估结果更加真实全面。可见,动态风险评估已为人们所关注。
目前的桥梁施工风险评估仍以静态评估为主,难以反应风险因素之间的前后影响关系及随施工的动态变化情况;尤其在工艺复杂的大型桥梁工程中,风险因素多,前后影响关系更为复杂,既有风险动态方法难以准确、全面反映施工全过程中风险传递特点。为此,本文基于传统风险评估方法,引入决策评价与实验室(DEMATEL)算法,提出基于动态风险元识别、关联度分析构建风险元传递网,构建基于贝叶斯网络分析模型的风险动态评估方法,并以五峰山长江大桥施工风险评估为例开展详细的风险动态评估。
1 桥梁施工风险动态评估理论
1.1 风险元传递理论
某一风险事件发生,可能诱发一连串的次生、衍生风险事件发生,这种现象称为风险事件链[15]。大型桥梁工程施工复杂,其风险的发生大多数呈现风险事件链的特点,因此桥梁施工风险动态评估的实质是分析风险事件之间随施工工序推进的动态传递关系,与以往静态风险评估相比,动态评估突破风险事件独立发生的理论假设,将前后工序中风险事件间的动态传递特性引入评估中;但在大型桥梁施工全过程中,风险传递路径长,各风险变量之间的逻辑关系难以准确区分,风险传递下的条件概率难以精确量化。鉴于桥梁工程施工以各施工工序为基本组成形式,前面各工序中的若干风险因素直接、间接影响后续工序风险因素,故引入风险元传递理论来分析桥梁工程施工中风险变量动态传递关系,判别各施工工序中的具有前后影响关系的动态风险元,并构建包括链型、关系型、树型等网络结构的施工过程风险元传递网,。
1.2 基于DEMATEL 算法的动态评估风险元识别理论
既有的风险识别方法能够识别大型桥梁众多的风险因素,但也易造成评估计算分析困难。因此,根据风险因素关联度进行筛选处理,去除与大桥施工质量与安全目标关联性较小的因素,仅选取主要风险因素作为动态评估的风险元。DEMATEL 算法[16]能够依据因果关系从众多影响因素中识别出根本性的影响因素,有效解决复杂系统要素之间的关联问题。基于DEMATEL 算法识别动态评估风险元的具体理论方法如下:
(1)风险元影响矩阵计算,分为初始直接影响矩阵B、规范化直接影响矩阵C和综合影响矩阵T计算3步。首先,依据施工流程和工程需要划定风险动态评估具体项目,采用事故统计法和WBS‒RBS 等完成初步风险元识别工作;其次,构建初始直接影响矩阵B,基于相互关联关系评价标准(采用国际通用的0、1、2、3、4五级标度法分别表征极弱、较弱、一般、较强、极强关联性),依托事故统计结果或专家经验获得风险元之间的直接影响矩阵Bk(βk=[βkij]n×n),矩阵中βkij表示第k 位专家对风险元ai对aj的关联程度的评定结果,当i=j时,取βkij=0,对于多位专家的评价数据采用取平均数的方法获得矩阵B(βk=[βij]n×n)中其余元素值,并结合矩阵B 中行和最大值,得到规范化直接影响矩阵C,计算公式为
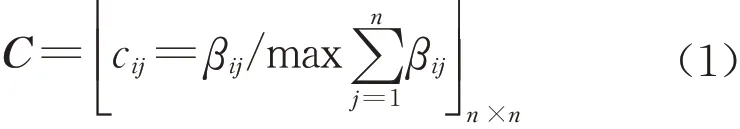
Cn(C 的n次自乘)表示风险元之间增加的间接影响,当把所有的风险元的直接影响及间接影响相加时,即得综合影响矩阵T=C1+C2+…+Cn,从而确定出每个风险元在系统中影响程度。
(2)风险元参数计算。针对风险元i,首先计算其对其他所有风险元的影响度fi,将矩阵T中元素按行求和可得其影响度fi;其次计算反映风险元i 受其他所有风险元影响度程度的被影响度ei,将矩阵T中元素按列求和可得被影响度ei,最后计算中心度Mi和原因度Ni,计算风险元i 的影响度fi和被影响度ei之和得到其中心度Mi,计算风险元i的影响度fi与被影响度ei之差可得其原因度Ni。
(3)动态评估风险元识别。风险元参数计算结果中,中心度表示风险元ai在所有风险元中的重要性程度,中心度越大,风险元重要性则越高;而原因度则表示风险元ai对其他所有风险元的影响,即与其他风险元的因果逻辑关系,若为正,表示该风险元对其他风险元的影响大,称为原因风险元,若为负,则表示该风险元受其他风险元的影响大,称为结果风险元。依据中心度大小得到各风险元的重要性排序,为了客观衡量风险元在评估系统中影响强度大小,参考阈值设定中的象限法以及风险等级划分时的均分原则,设定风险元影响强度量化标准如表1所示。在识别动态评估风险元时,根据表1 中强度量化标准,并参考现场工程实际设定阈值,选取关键风险元完成识别。

表1 风险元影响强度量化标准Tab.1 Quantitative standard of risk element impact intensity
1.3 风险元传递网络构建方法
风险元传递网构建采用关联关系分析为主、因果关系推理作为补充的方法。关联关系分析是依据专家知识和经验确定的关联度等级来判定主要风险元间的传递关系;因果关系推理则是逻辑分析方法,以衡量次要风险元之间的微弱关联。风险元传递网构建时,首先根据关联度等级判断风险元之间的传递关系,所有风险元之间关联等级评定是在初始直接影响矩阵B 中根据专家知识完成,当矩阵中B 元素βij大于等于2时,表明风险元ai对aj的关联程度具有一般及以上等级的关联性,判定风险元ai对aj构成风险传递关系,形成初步的风险元传递网。其次采用因果关系推理对初步风险元传递网进行修正完善,利用故障树分析法中逻辑与门和或门的特性[3],结合工程现场风险控制来检核风险元之间的微弱关联,解决少量施工中影响强度高的风险元因其仅与多个风险元有较弱的关联性导致打分均值低于2而判定没有传递关系的问题。
1.4 基于贝叶斯网络的施工风险动态评估理论
贝叶斯网络在不确定性知识表达和推理领域具有的极大优越性[17],适用于风险动态评估模型中对风险元传递网的分析。贝叶斯网络由网络结构和网络参数两部分组成,贝叶斯网络结构由节点和有向边组成,节点表示随机变量,有向边表示节点之间的因果关系。有向边由父节点指向子节点,以父节点表示条件,子节点表示结果。贝叶斯网络参数是对节点之间的依赖关系强度的描述,通常用条件概率和先验概率表示。风险评估中应用贝叶斯网络描绘风险元传递关系,并通过条件概率量化风险元之间的传递效果,此外借助推理分析,以正、反向推理和辅助决策推理(敏感性分析)3种推理方式,分别对风险元传递网展开概率预测计算、风险链诊断和关键风险元分析,实现风险动态评估。详细的风险动态评估方法如下:
(1)贝叶斯网络构建。因识别的风险元传递网节点之间是以因果关系为基础构建,故将风险元传递网直接映射为贝叶斯网络,其中每个节点作为随机变量,存在“Y”发生和“N”不发生两种状态。在确定贝叶斯网络结构之后进一步确定贝叶斯网络参数,即求解贝叶斯网络中相关父节点的先验概率和父子节点之间条件概率。如果存在大量数据,可通过参数学习确定网络参数具体值,但桥梁工程风险评估多采用事故调查法、专家调查表法形式进行概率量化,故将识别出的风险元制成表,以事故样本案例统计结果或邀请若干有经验的业内专家进行评估,并结合《公路桥梁和隧道工程设计安全风险评估指南》和国际隧道协会《Guidelines for Tunneling Risk Management》中的概率标准制定“不可能、很少、偶然、可能、很可能”5 个概率评判等级,分别对应“<0.000 3、0.000 3~0.003、0.003~0.03、0.03~0.3、>0.3”概率范围及“0.000 1、0.001、0.01、0.1、0.9”中心值。评估时采用专家“评判等级”描述对应的概率中心值,计算先验概率节点j的概率Pj为

式中:n 为所邀请专家总人数;ni为认为风险元发生概率等级i的专家人数;Bi为概率等级i的中心值。
条件概率反映了父节点处于不同状态时子节点处于特定状态的概率。计算条件概率时,设父节点为M、子节点为K,当M节点处于Y状态时子节点K处于N状态的概率PMY‒KN计算公式为
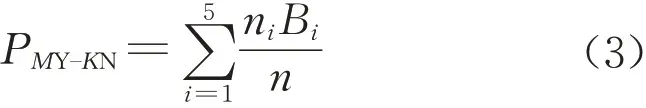
(2)贝叶斯网络推理分析,包括正向推理、逆向推理及敏感性分析。首先进行正向推理,即风险元概率等级计算。设贝叶斯网络节点T的父节点变量为Cj(j=1,2,3),Cj的状态分别用CjY和CjN表示发生和不发生状态,用T=Y和T=N分别表示子节点T处于发生和不发生状态。贝叶斯网络中通过联合概率公式计算出父节点不同状态下子节点发生概率,从而对风险传递网各风险元概率等级进行预测。其中若已知各父节点状态以及相应的概率,则节点T 处于Y 状态的概率P(T=Y|Cj=Y)表示贝叶斯网络向前传导的条件概率,可通过已知的中间节点联合概率P(T=Y,Cj=Y)与中间节点联合概率P(Cj=Y)的比值计算而得。
(3)逆向推理,主要识别风险元传递链。逆向推理时已知子节点T 发生状态,根据条件概率公式计算各个父节点Cj的后验概率分布,并根据其量值大小构建传递链。Cj后验概率P(Cj=Y|T=Y)可由Cj处于Y 状态先验概率P(Cj= Y)与条件概率P(T=Y|Cj=Y)的乘积与T 处于Y 状态先验概率P(T=Y)的比值计算而得。
(4)敏感性分析,即关键风险元识别。贝叶斯网络中敏感度反映父节点状态的变化对子节点状态的平均影响程度,反映了风险元传递网络中影响目标节点的关键风险元。节点Cj处于Y发生状态的敏感性计算公式为

2 桥梁施工风险动态评估方法流程
桥梁施工风险动态评估由动态评估风险元识别和动态风险评估两部分组成。动态风险元识别中,先在资料收集与工程特点分析的基础上进行基于WBS‒RBS 方法的初步风险元识别,形成初步风险元清单。基于初步风险元识别结果,调研事故案例及邀请专家对风险元之间的关联度进行评定,汇总调研评估结果形成关联矩阵B,即DEMATEL 算法中初始直接影响矩阵B。之后,采用DEMATEL 算法计算风险元的影响度fi和被影响度ei以及风险元的中心度Mi和原因度Ni。进而对初步风险元的中心度进行排序处理,从而完成动态评估风险元识别。在风险元识别结果及其关联度分析的基础上,结合不同施工工序风险元的前后影响关系构建风险元传递网,并采用贝叶斯网络构建模型对其评估,最后通过贝叶斯网正向推理、逆向推理、敏感性分析计算出风险元节点先验概率、后验概率、敏感性值,并识别出主要风险元传递链和关键风险元。评估流程如图1所示。
3 五峰山长江大桥施工风险动态评估
3.1 工程简介
连镇铁路五峰山长江大桥主桥长1 432 m,正桥主航道桥为(84.0+84.0+1 092.0+84.0+84.0)m双塔连续钢桁架悬索桥,为公铁两用桥,承载4线高速铁路及8线高速公路。大桥北锚碇采用沉井扩大基础,其长宽分别为100.7 m、72.1 m,面积巨大。南锚碇为直径90.0 m 圆形变高度地下连续墙围护现浇扩大基础。大桥主塔墩采用梅花式布置的不等高群桩基础,桩长65.0~135.0 m。南北承台形状呈哑铃型,采用钢板桩围堰和钢围堰分别浇筑施工。两边主塔均采用钢筋混凝土门式框架类型,北主塔高度为203.0 m,南主塔高度为191.0 m。大桥主缆采用预制平行高强钢丝索股(PPWS)结构,主缆挤圆后理论直径为1.3 m。大桥主梁采用了板桁结合钢桁梁的形式,最重施工节段重1 760 t。大桥立面布置如图2所示。
五峰山长江大桥结构特殊、规模庞大,南北锚碇基础面积、主缆直径及受力、主梁承载等参数远超出现有桥梁,施工采用众多新设备、新工艺,可借鉴的工程案例较少,大桥施工全过程中面临的挑战与风险显著,开展施工风险动态评估尤为必要。
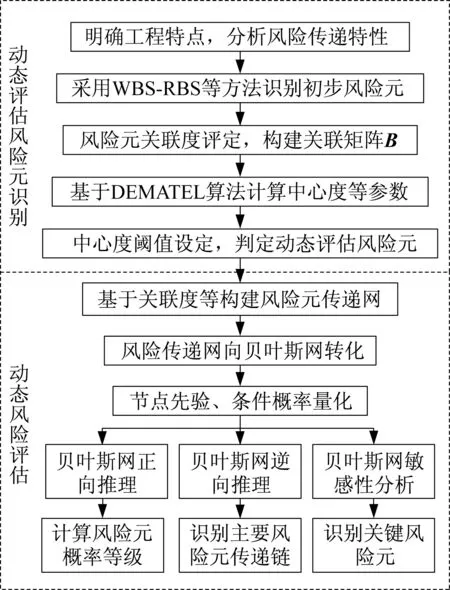
图1 桥梁施工风险动态评估方法流程Fig.1 Process of dynamic assessment method for bridge construction risks
3.2 动态风险元识别
针对五峰山长江大桥采用WBS‒RBS和专家调查法相结合的方法[18]完成全桥施工过程中风险元初步识别及评估工作,识别时共分解为沉井基础施工、桥塔施工、主缆架设、主梁架设等10 个分项78 个基础工序,从建设条件、结构方案、施工工艺和运营维护4个方面识别出610项风险元,结合评估出的中等风险和重大风险,对其中24个重要施工工序进行动态风险评估。编写DEMATEL算法计算程序,依据风险元之间关联度调查结果,逐步计算初始直接影响矩阵B、规范化直接影响矩阵C 和综合影响矩阵T,之后将T 中元素按行、列分别求和得风险元的影响度fi和被影响度ei,将影响度和被影响度相加即得中心度Mi,相减即得原因度Ni,以中心度大小为主要依据对各评估工序风险元排序,通过设定中心度阈值选取动态评估风险元。
由于全桥施工的风险元数量庞大,仅以主缆架设施工为例介绍风险动态评估过程。主缆索股架设施工如图3所示。主缆索股施工动态风险元初步识别有26 个,通过程序计算出相应中心度和原因度值,并依据中心度大小完成风险元排序。采用表1中风险元影响强度量化标准,以处在中、弱影响强度等级之间风险元为分界点,设定中心度阈值。索股施工中中心度排序为17 的风险元“卷扬机故障”排序在60%以后,在系统中影响强度为“弱”等级,表明该风险元对其余风险元传递效应可以忽略,因此排序在17~26 之间的风险元不做考虑,相应地设定中心度阈值为2,选定“塔顶索股提升损伤Rc16”及之前风险元作为风险动态评估中风险元,详细结果见表2。
根据DEMATEL算法分类规则,全部风险元分为原因型(原因度为正值)和结果型(原因度为负值)两大类,原因风险元对结果风险元产生影响;且某风险元中心度排序越靠前,该风险元与其他风险元关联性越密切,重要性越高。表2中“索股线形Rc1”中心度为排序第一,说明在主缆架设施工中索股线形重要性最高,影响施工程度最深,其原因度为负值,为结果风险元,则表明在施工中该风险元受其他风险元影响程度大。此外,“索股线形监测方案设计Rc2”中心度值为排序第二,虽然重要性较高,但原因度是正数,是原因风险元,所以该风险元在传递时主要影响其他风险元,可认为是造成索股施工风险传递的重要因素。
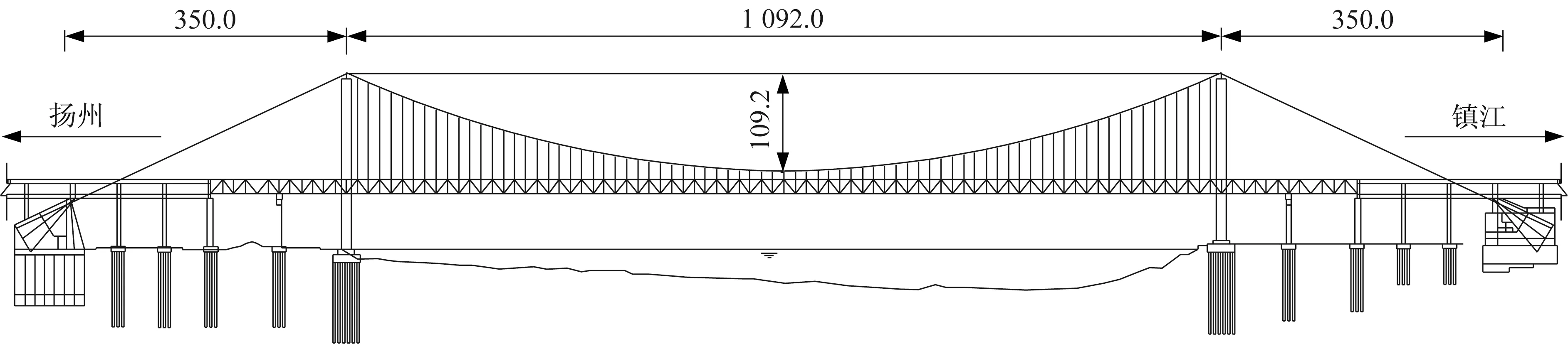
图2 五峰山长江大桥主桥立面图(单位:m)Fig.2 The elevation of the main bridge of Wufengshan Yangtze River Bridge (unit:m)
全桥施工过程共在24 个重要工序评估中识别出234 个风险元参与动态风险评估,并据此选取各工序中部分具有代表性的风险元作为全桥动态评估风险元,部分识别结果见表3。识别时先参考风险元中心度和原因度,如沉井施工中“沉井就位几何姿态偏差R1”重要性最高,且作为沉井施工中结果风险元将风险传递给下一个工序;其次,结合桥梁结构传力规律,如“索夹滑移R14”中心度值仅为2.03,重要性相对较低,但索夹是重要传力部件必须考虑该风险元的影响;最后,从结构运营维护角度识别,如风险元“南锚碇不均匀沉降R3”在锚体施工时,中心度值相比“锚固系统安装偏差R8”较低,重要性不突出,但其影响后续施工及运营安全,因此予以识别。

图3 主缆索股架设施工Fig.3 Erection construction of main cable strands
3.3 风险元传递网构建
风险元传递网构建时,首先结合初始直接影响矩阵B 中关联度评定结果,如“塔顶索股提升损伤Rc16”对“索股损伤Rc13”的关联度值为2.6,则判定两者之间存在传递性,据此逐步形成初步的风险元传递网;其次,以因果关系推理结合工程实际对风险元传递网进行修正,如“雷雨大风干扰Rc8”对“索股线形标志点损坏Rc11”、“线形监测误差Rc10”和“一般索股架设偏差Rc4”关联度评定结果均处于2 以下,根据逻辑与门和或门分析可知,Rc8与Rc11以及Rc10之间表现为逻辑与门关系,即施工现场未对标志点复查以及监测数据复测时,会导致Rc4发生,而Rc8与Rc4之间则为逻辑或门,索股架设过程中若是突发雷雨天气,此时无论采取何种措施索股架设精度必然受到影响,因此判定Rc8 与Rc4 之间存在传递关系。构建索股施工动态评估风险元传递网,如图4 所示。主缆架设工序中的部分风险元“索股线形Rc1”和“索股损伤Rc13”等将继续传递给后续工序。依据各施工工序中的风险元,如沉井施工中“沉井就位几何姿态偏差R1”、“沉井不均匀沉降R2”和索夹施工中“索夹滑移R14”等,同理可构建全桥风险元传递网(部分),如图5所示。
3.4 贝叶斯网络的建立
贝叶斯网络评估以图4所示主缆索股施工风险传递链网为例,将其直接映射为贝叶斯网络结构,网络中各节点均采用二元“Y(风险元发生)和N(风险元不发生)”的表征方式。图4对应的贝叶斯网模型中各节点的先验概率和条件概率先通过问卷调查方式获得初步结果,后根据式(2)、(3)进行处理并汇总。节点间的条件概率表以风险元Rc13 在风险元Rc3、Rc14、Rc15 下的条件概率为例,其中,风险元“基准索股安装精度Rc3”处在Y 状态的概率为0.000 4,对应风险概率标准可知,其概率等级为2级。当风险元Rc3、Rc14、Rc15 均处于Y 状态时,风险元Rc13处于Y状态的概率为1.00,处于必然发生状态;而当风险元Rc15 变为N 状态时,风险元Rc13处在Y 状态的概率也随之减小,为0.73;当风险元Rc3、Rc14、Rc15 均变为N 状态,风险元Rc13 处在Y状态的概率为0,即必然不会发生。

表2 主缆架设风险元识别结果Tab.2 Results of risk element identification of main cable erection

表3 全桥部分动态风险元(部分)识别结果Tab.3 Partial identified dynamical risks of whole bridge

图4 主缆索股施工风险元传递网Fig.4 Construction risk element transmission
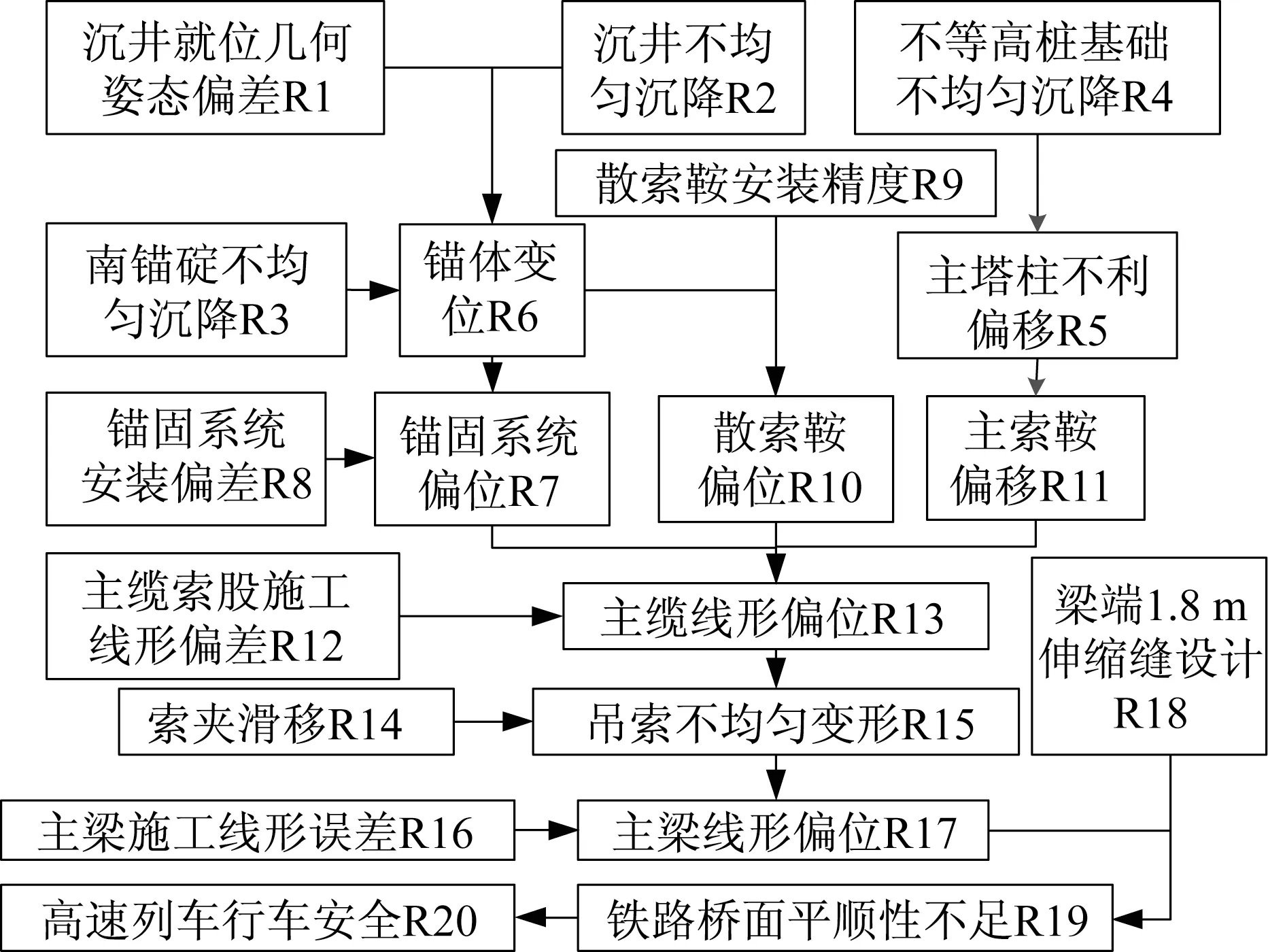
图5 全桥关键风险元传递网(部分)Fig.5 Transmission network of key risk element
3.5 风险概率计算结果与风险链评估
贝叶斯网络模型评估过程以主缆索股架设施工为具体算例,具体评估结果如下:
(1)正向推理及风险元概率计算。将节点先验概率和条件概率输入软件GeNIe 中,得到主缆索股施工风险传递网中各风险元的概率,结果如表4 所示。表4中结果风险元“索股损伤Rc13”发生概率为0.015 2,“索股线形Rc1”发生概率为0.010 5,两者均处于偶然发生状态,说明索股施工质量风险突出。“线形监测误差Rc10”同时受到风险元Rc2、Rc3、Rc7、Rc11 的影响,发生概率为0.012 7,应在施工中重点关注。
(2)逆向推理及主要风险传递链识别。采用贝叶斯网络中逆向推理确定主要风险元传递链,设置“索股线形Rc1”和“索股损伤Rc13”为目标节点(P(Rc1、Rc13=Y)=1),分析结果如表4所示。表4中先验概率和后验概率值均为风险元处于Y状态的概率值。根据表4 中风险元后验概率大小,结合风险元传递网可知,对索股损伤产生传递效应的风险元Rc14、Rc15和Rc16中,索股牵拉不平顺损伤Rc14容易导致索股发生损伤;在索股线形发生偏差风险时,风险元“1.3 m大直径主缆设计Rc6”的后验概率值达到0.92,表明主缆采用1.3 m 大直径的特殊设计,导致索股线形监测、垂度调整困难风险急剧上升,与实际工程相符;因此根据表4中风险元后验概率大小,以节点Rc1和Rc13为初始节点,结合图4中风险元传递网逐层比较判断,得到索股施工中2 条主要的风险元传递链,分别为:①索股牵拉不平顺、鼓丝Rc14→索股损伤Rc13;②1.3 m 大直径主缆设计Rc6→索股线形监测方案设计Rc2→线形监测误差Rc10→索股线形计算偏差Rc5→一般索股架设偏差Rc4→索股垂度调整偏差Rc12→索股线形Rc1。
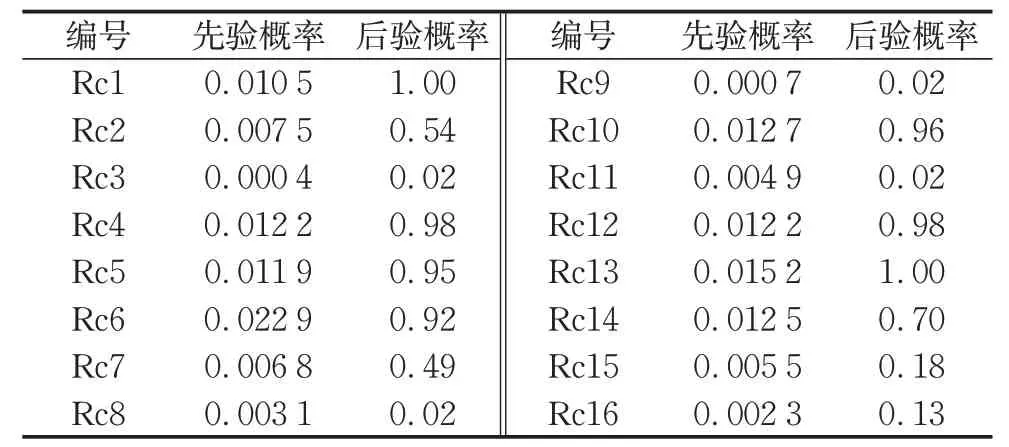
表4 索股架设施工风险元概率计算结果Tab.4 Results of risk element probability calcula⁃tion of cable strand erection
(3)敏感性分析及关键风险元识别。将“索股线形Rc1”和“索股损伤Rc13”节点设置为目标节点,进行敏感性分析,系统自动计算灵敏度值。结果表明,影响“索股损伤Rc13”的关键风险元为“索股牵拉不平顺、鼓丝Rc14”和“塔顶索股提升损伤Rc16”;影响索股线性的关键风险元为“基准索股安装精度Rc3”、“索股线形标志点损坏Rc11”、“雷雨大风干扰Rc8”、“鞍座偏移Rc9”和“1.3 m 大直径主缆设计Rc6”。
对于大桥施工全过程,在完成包括索股架设施工在内24个工序的动态评估之后,汇总大桥各个工序动态风险评估结果,进行全桥施工前的风险动态评估,并根据施工工序推进中风险元实际发生与否(Y、N状态)更新评估其后风险元概率。部分关键风险元在施工前及代表性工序后的概率计算结果如表5 所示,其中施工前结果风险元“高速铁路行车安全R20”发生概率最高值为0.065 2,风险元“主梁线形偏位R17”发生概率值为0.063 9,“铁路桥面平顺性不足R19”发生概率值为0.064 2,均处于很可能发生状态,风险概率计算结果表明,大桥施工面临较大挑战。对比不考虑全桥风险传递并假定主梁线形无风险时计算出“铁路桥面平顺性不足R19”概率值0.006 1,风险发生概率差值达到0.058 1,可见动态风险传递效应明显。在实际施工过程中,随着各工序相继完成,相关风险元得到良好控制而未发生,以“不可能发生”状态对应中心概率值0.000 1,调整贝叶斯网节点先验和条件概率值,结果表明,随着施工中及时有效的风险控制,节点R19、R20 风险概率值分别下降到0.010 8、0.009 1,处于偶然发生状态。
主要风险传递链识别采用贝叶斯逆向推理的方法,设置“高速铁路行车安全R20”为目标节点,部分风险元后验概率计算结果如表5所示。根据后验概率值排序得到最重要的2 条传递链为:①沉井不均匀沉降R2→锚体变位R6→锚固系统偏位R7→主缆线形偏位R13→吊索不均匀变形R15→主梁线形偏位R17→铁路桥面平顺性不足R19→高速铁路行车安全R20;②不等高桩基础不利沉降R4→主塔柱不利偏移R5→主索鞍偏移R11→主缆线形偏位R13→吊索不均匀变形R15→主梁线形偏位R17→铁路桥面平顺性不足R19→高速铁路行车安全R20。
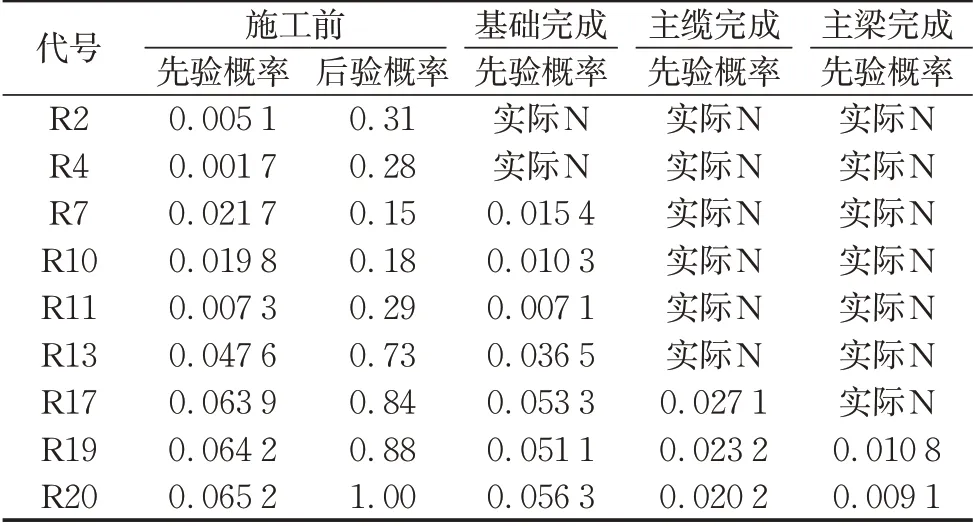
表5 全桥部分风险元概率动态计算结果Tab.5 Results of dynamic probability calculation of partial risk element of whole bridge
采用贝叶斯敏感性分析,识别出全桥各工序中关键风险元共计104 个,其中针对全桥风险元传递网分析时,以结果风险元“高速铁路行车安全R20”为敏感性分析目标节点,依据分析结果得到易对行车安全造成影响的风险元依次为:沉井不均匀沉降R2、不等高桩基础不利沉降R4、主缆线形偏位R13,表明在施工及后续运营中,应重点加强不等高桩基础、主缆和沉井的位移及变形监测,以保证大桥安全长期运营。
4 结论
针对大型桥梁工程施工中风险因素之间前后动态影响关系问题,引入风险元传递理论,并提出了一种风险动态评估方法,通过对五峰山长江大桥施工展开动态风险评估,得到如下结论:
(1)基于决策与实验室(DEMATEL)算法,在初步风险元识别结果基础上,利用中心度排序去除了低关联度风险元后,识别出其中关键风险元参与动态评估,并以风险元关联度分析及因果关系推理建立风险元传递网。
(2)采用贝叶斯网络法评估大桥风险元传递网,以专家调查获取贝叶斯网独立、条件概率,计算风险元传递网概率等级,并结合敏感性分析和逆向推理识别关键风险元及主要风险元传递链。
(3)五峰山长江大桥施工动态风险评估研究中,基于DEMATEL算法共识别出234个动态评估风险元,依据关联度方法构建出24 个风险元传递网,同时辨析出104 个关键风险元;计算出施工前及主梁完成后“高速铁路行车安全”风险概率值分别为0.065 2、0.009 1,对应的关键风险元为沉井不均匀沉降、主缆线形偏差等,其中主要风险元传递链为:沉井不均匀沉降R2→锚体变位R6→锚固系统偏位R7→主缆线形偏位R13→吊索不均匀变形R15→主梁线形偏位R17→铁路桥面平顺性不足R19→高速铁路行车安全R20。
(4)通过五峰山长江大桥施工实例,揭示了施工风险发生的传递机理,评估出的风险元传递链和关键风险元,验证了动态风险评估模型的可靠性,可为复杂的大型桥梁工程的施工风险评估与控制提供参考。
作者贡献说明:
施 洲:通信作者,提出动态评估模型,对论文提出了建设性建议,并作修改。
纪 锋:工程现场调研,扩展完善动态评估模型,撰写论文初稿并修改。
余万庆:工程现场调研,处理专家调查数据,修改论文。
韦庆东:协调大桥施工现场风险调研,邀请并组织专家对评估中关联度和贝叶斯网概率进行打分评定。
