液力变矩器叶片厚度及冲角适配减速带捕能装置

2021-05-14薛松杰葛传洁

应用能源技术 2021年3期

罗政，薛松杰，葛传洁

(华北电力大学动力工程系，保定 071003)

0 引言

随着人类社会和科学技术的不断发展，“能源危机”逐渐成为限制人类社会的主要问题。而在这样的环境大背景下，不断寻找新的可替代能源和减少能量消耗成为社会应对能源危机的主旋律。为此，用来使汽车减速的减速带受到了人们的关注。城市路口、高速路口集中分布了许多的减速带，如果能将减速带损失的这一部分能量加以利用，也是对捕获能量的一种新的想法。而液力变矩器作为一种液压传动装置和减速带能量捕获装置组合的适配也就成为了一个问题。针对以上问题国内外学者做了以下研究。刘迪在液力变矩器循环圆直径不变的情况下，通过优化泵轮叶片形状，增加泵轮出口叶片角，增加泵轮力矩系数的办法，使液力变矩器在低速比时具有高效率的性质[1]；刘安然对长短叶片泵轮对外特性的影响进行研究，发现长短叶片泵轮对外特性的改善起到积极作用，在转速比在0.519～0.692之间效率值增加1.31%～2.72%，启动工况变矩比k由3.91 提高到4.1[2]；罗准等对具体的减速带装置和双液压缸式换能器进行了建模，利用Amesim进行数值计算，建立了气缸内径、储能器气体体积等参数与减速带弹簧刚度等参数的关系[3]；Darrell Robinette针对液力变矩器对于汽车运行的适配性做了研究，对三个具有近似精确几何相似度的变矩器进行了尺寸分析，以显示相关性在预测整体外部对流换热机制中的适用性[4]。

总体而言，对于减速带建模，液力变矩器建模和数值模拟的研究已经相对成熟，但对于液力变矩器和减速带的适配问题的研究还不多见。文中通过对液力变矩器进行建模分析，研究变矩器叶片厚度对常见减速带能量捕获装置的适配性，并利用模拟退火算法，寻求最优解。研究结果可为液力变矩器使用在其他领域的适配问题提供参考。

1 模型建立及实验工况设置

国内外对于液力变矩器的叶片厚度、冲角适配的研究并不多见，文中以等叶片厚度的冲焊型液力变矩器为研究对象，采用ANSYS-CFX软件对本问题进行数值模拟，研究叶片厚度、叶片冲角对于变矩器工作性能的影响。试验因素为泵轮叶片厚度、涡轮叶片厚度、各叶片冲角，参考某冲焊型液力变矩器相关参数[5]，设置具体实验变量(见表1,表2)。Tp为泵轮叶片厚度，Tt为涡轮叶片厚度，αP为泵轮叶片冲角，αT为涡轮叶片冲角，αS为导轮叶片冲角。由于试验中的因素个数较少，所以采用全因素试验方法，评估所有因素在所有水平上的可能组合。

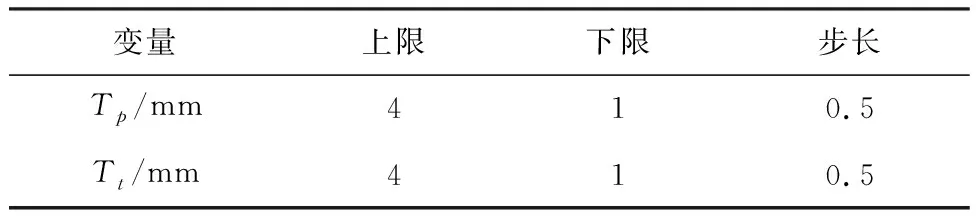
表1 冲焊型液力变矩器实验参数

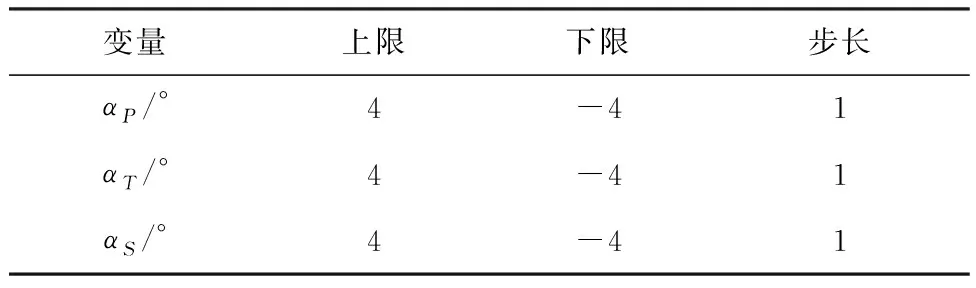
表2 变矩器叶片冲角实验参数

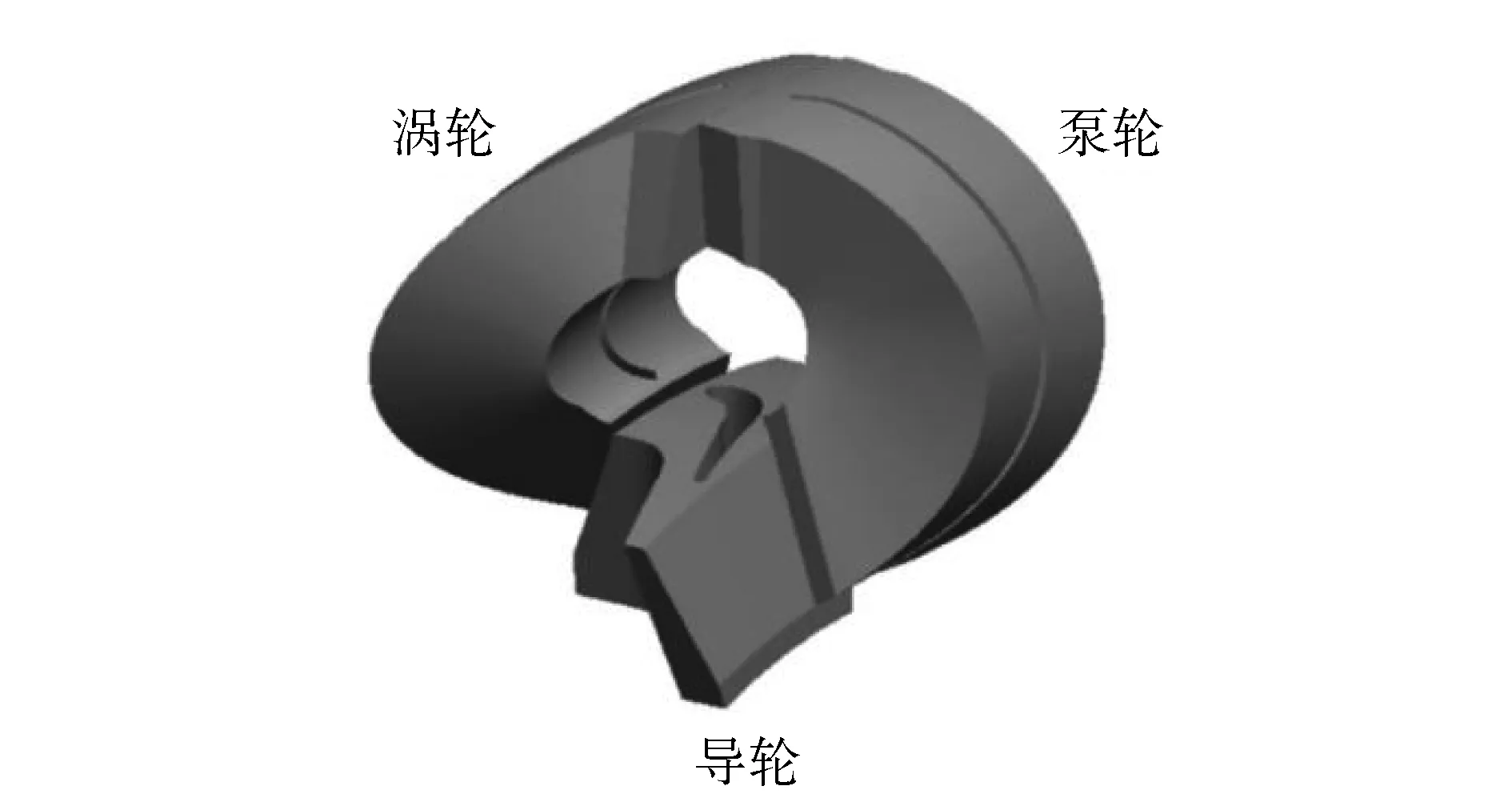
图1 液力变矩器单通道物理模型

分析采用ANSYS-CFX进行计算，对于单流道模型建立图一中的物理模型，如图1，图2所示。采用ICEM对物理模型进行网格化离散处理，处理结果网格数为322万。将网格导入后，检查网格质量为0.76，可以满足本问题计算需求。对于计算模型进行选择，由于研究问题是一个稳态的流动问题，选择以压力为基础的绝对速度稳态模型。算法模型选择能量方程和k-epsilon-SST湍流模型，而离散形式选择更容易收敛的一阶迎风格式，松弛因子选用默认值。固体域选用常见金属材料钢，内部流动液体选用22号透平油。对于边界条件：入口设置为压力入口，温度为368 K，相对压力为0.07 MPa；出口设置为速度出口；对于壳内壁面，设置为绝热边界无滑移，温度350 K。

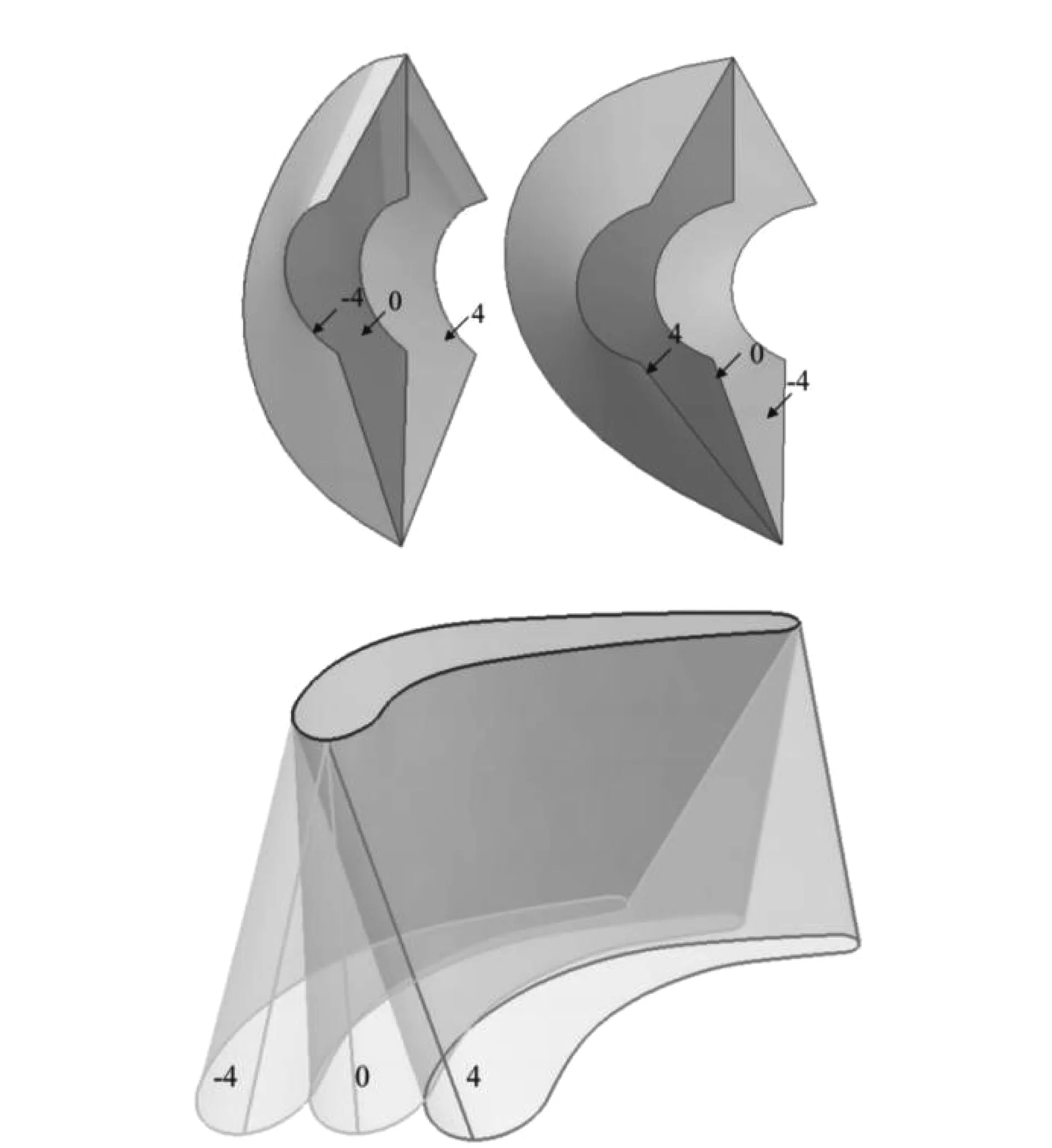
图2 液力变矩器各叶片物理模型(左泵轮，中涡轮，右导轮)

2 结果分析

参考流场分析结果，共设置三个响应量，最高效率ηmax，最大能容系数λ0max，起动变矩比K0，输出转矩To。基于闫东清[5]对主效应、交互效应的相关研究，涡轮叶片厚度和泵轮叶片厚度虽然对效率有交互影响作用，但其对于变矩器的影响主要还是集中在涡轮和泵轮的输出转矩上，故将输出转矩作为评判变矩器性能的指标。

2.1 叶片厚度对泵轮输出转矩的影响

根据不同情况，分别取泵轮叶片厚度Tp为定值2 mm，涡轮叶片厚度Ts为定值2 mm，速比为0.2，研究泵轮输出转矩的变化。为研究两者交互影响，以及所有水平上可能的两个叶片厚度的组合变化，获得其对泵轮输出转矩的影响规律。叶片厚度对泵轮输出转矩的影响如图3所示，涡轮、泵轮叶片对泵轮输出转矩的交互影响如图4所示。

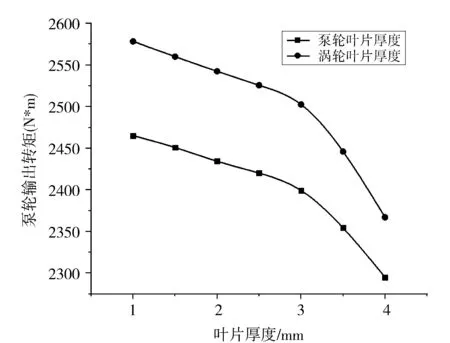
图3 叶片厚度对泵轮输出转矩的影响

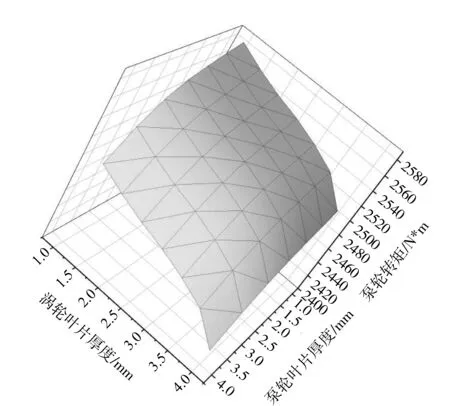
图4 涡轮、泵轮叶片对泵轮输出转矩的交互影响

根据不同叶片厚度下泵轮转矩数值的对比图，无论是涡轮叶片厚度增加或者泵轮叶片厚度增加都会导致输出转矩的减小，这种趋势再叶片厚度较大时更为明显。由于叶片厚度加厚，导致边界层分离点后移，产生启动涡需要更大的逆压力梯度，导致了输出转矩的变小。在1～ 3 mm的范围内泵轮输出转矩的变化平均为2%，最大值为2.3%，在3～4 mm范围内泵轮输出转矩的平均变化率为3%，最大值为3.8%。且对于泵轮输出转矩，改变泵轮叶片厚度时，输出转矩始终低于同水平涡轮7%左右。

2.2 叶片厚度对涡轮输出转矩的影响

分别取泵轮叶片厚度Tp为定值2 mm和涡轮叶片厚度Ts为定值2 mm，速比为0.2，研究泵轮输出转矩的变化。为研究两者交互影响，以及所有水平上可能的两个叶片厚度的组合变化，分析其对涡轮输出转矩的影响。叶片厚度对涡轮输出转矩的影响如图5所示，涡轮、泵轮叶片对涡轮输出转矩的交互影响如图6所示。

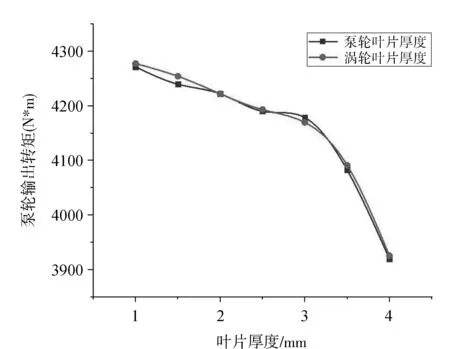
图5 叶片厚度对涡轮输出转矩的影响

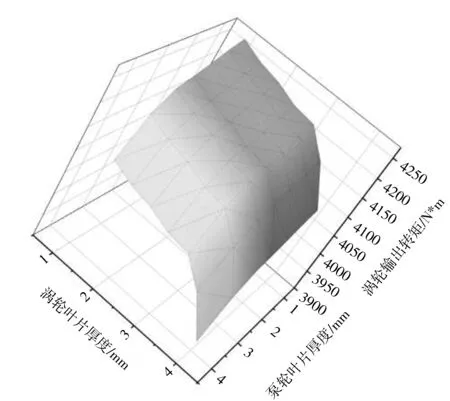
图6 涡轮、泵轮叶片对涡轮输出转矩的交互影响

根据不同叶片厚度下涡轮转矩数值的对比图，不同于泵轮，涡轮输出功率对于两种叶片厚度变化的响应差异不大，原因为涡轮和泵轮功能上本质的不同，涡轮将输入不稳定的机械能转化成稳定压力势能，泵轮将压力势能转化成稳定的机械能，所以两者对转矩的响应呈不同趋势。同时无论是涡轮叶片厚度增加或者泵轮叶片厚度增加都会导致输出转矩的减小，这种趋势在叶片厚度较大时更为明显，涡轮在1～3 mm的范围内泵轮输出转矩的变化平均为2.2%，最大值为2.5%，在3～4 mm范围内泵轮输出转矩的平均变化率为3.4%，最大值为4.2%。

2.3 叶片冲角对变矩器工作性能的影响

由于改变冲角对输出转矩的影响并不明显，为研究导轮、泵轮、涡轮不同叶片冲角对液力变矩器性能的影响，更换泵轮转矩系数作为响应量，保持其它设计参数不变，改变叶片冲角的数值，更新模型，分别划分网格，建立流场仿真计算模型，采用相同的流场仿真方法开展研究。叶片冲角对泵轮转矩系数的影响如图7所示。

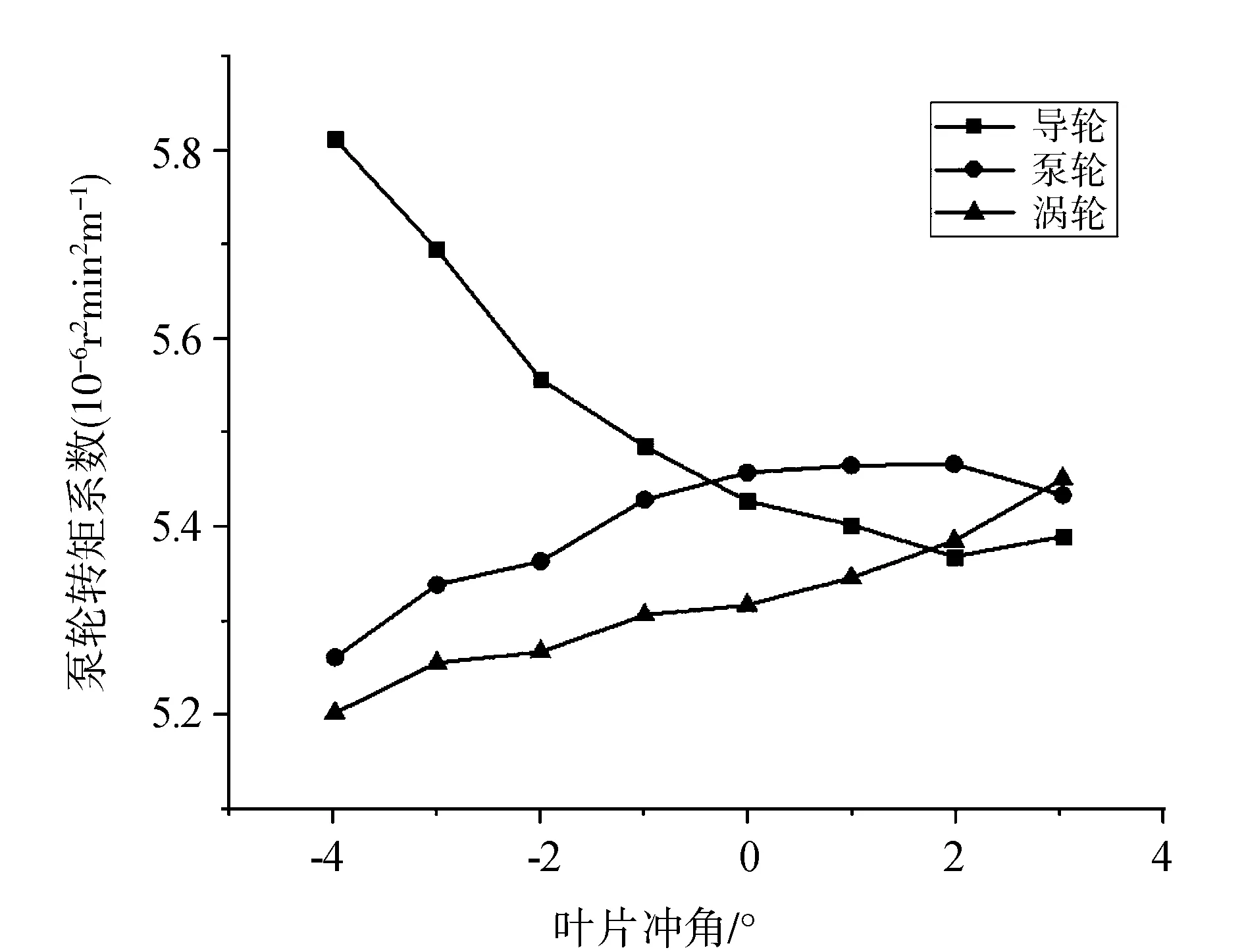
图7 各叶片冲角对泵轮转矩系数的影响

不同类型的叶片的冲角对液力变矩器泵轮转矩系数的影响不同，对于涡轮叶片，冲角增大，转矩系数逐渐增长，增长总体水平一致，平均变化率1.4%。对于泵轮叶片，冲角增大，转矩系数先增大后减小，转矩系数最大值5.5，此时冲角为2°。对于导轮叶片，冲角增大，转矩系数总体呈减小，后有略微增大，转矩系数最小值为5.35，此时冲角为2°。