公平高效的安全双边云资源拍卖方案
2021-05-14沈玉龙高晟凯徐振楠
段 靓 沈玉龙 高晟凯 徐振楠
1(河海大学计算机与信息学院 江苏 南京 210098) 2(西安电子科技大学计算机科学与技术学院 陕西 西安 710071) 3(网联清算有限公司 北京 100045)
0 引 言
拍卖作为一种高效的云资源交易模式,被诸多主流云虚拟机提供商采用[1]。例如,Amazon公司在Amazon EC2平台中使用了拍卖机制来分配虚拟机(VM)并对其定价[2]。然而,现有的大多数云虚拟机拍卖方案(或称为云资源拍卖)只关注经济特性,例如真实性(Truthfulness)与社会福利最大化(Social welfare maximization),而忽略了隐私保护的内在需求,直接将竞拍信息暴露在全体拍卖参与者面前,而敏感竞拍信息的泄露会影响拍卖系统的正常运行。
云虚拟机通常是在有限且固定的时间单元内进行分配的,因此云虚拟机拍卖被认为是一个连续过程[3-4]。买卖双方可以通过不断监测和分析其他参与者的历史出价,调整其真实出价以获得更高的利润;拍卖商也可以根据历史出价主动调整定价策略以增加收益;恶意竞标者还可以根据历史出价提交一个精心设计的竞标价格,从而扰乱整个拍卖市场。所以,拍卖过程中敏感信息的泄露将会造成巨大的经济损失。
目前,已经有学者对安全拍卖问题展开了研究。Naor等[5]率先基于密码学工具构建了简易通用的安全拍卖框架;Suzuki等[6]基于同态密码构造了一种安全的广义二次拍卖模型,但这些方案均没有针对具体应用场景进行设计,并不能直接实际应用。针对具体拍卖场景的安全拍卖研究是近年来的热点,其中安全频谱拍卖、安全云资源拍卖得到了广泛关注。Chen等[7]基于秘密分享技术提出了一种信息论安全的频谱拍卖方案,但是该方案只能适用于单边市场情形下(即只存在单个卖方)的频谱拍卖。Wang等[8]针对双边市场下(即存在多个卖方)的安全频谱拍卖问题,基于半同态加密设计了一种竞价隐私保护的拍卖方案。Chen等[9]首次在安全频谱拍卖中考虑到了公平支付的问题,并基于可验证计算技术提出了相应解决方案。此外,安全云虚拟机拍卖也得到了广泛研究。Chen等[10]基于混淆电路(garbled circuit,GC)技术设计了一种隐私保护的云拍卖方案,然而该方案只适用于单边市场下的云拍卖,而非更实际的面向双边市场的云拍卖。Cheng等[11]结合秘密分享、同态加密等设计了一种混合式的安全双边云资源拍卖方案,使用两个不串谋的服务器构建而成,采用轻量级的加法秘密分享执行了大部分的线上安全操作,然而该方案线下阶段包含大量同态加解密与密文运算,整体效率较低,且通信开销过大。在其他领域也存在一些保护隐私的双重拍卖设计。然而,由于云虚拟机拍卖存在异构资源分配和实时性要求高等特殊需求,使得现有的工作无法满足安全云虚拟机拍卖的实际需求。因此,如何在不泄露隐私的情况下实现安全双边云资源拍卖仍然是一个难题。
拍卖的公平交易支付问题也是近年来的研究热点。目前,研究人员设计了一些基于区块链的拍卖方案,利用区块链去中心化特征,消除了拍卖中存在可信第三方问题。为确保投标价格的可靠性、公平性和交付过程中价格消息的安全性,Shu等[12]讨论将私有区块链应用到拍卖方案。Chen等[13]为避免电子投标系统中的第三方信任问题,提出了基于区块链的电子投标系统,利用智能合约处理投标交易,并确保投标过程的完整性。面向传统众包数据交易系统中心化信任问题,An等[14]提出了一种基于反向拍卖和区块链的众包数据交易系统(RADT),设计RADToken智能合约来强制不信任的各方诚实地参与数据交易。Franco等[15]提出一种基于区块链的反向拍卖架构(BRAIN),引入一种可审计的方法来降低网络功能虚拟化(NFV)技术商业化的成本,并分析其优缺点。Hassija等[16]提出了一种在客户和供应商之间进行能源交易的双重拍卖方案,通过智能合约实施分布式算法以最大化个人参与利润。Hassan等[17]开发了一种基于区块链的微电网能源拍卖方法,并使用差分隐私技术确保参与者私有信息的安全。然而,在云虚拟机拍卖领域,还没有切实可行的保证支付公平的拍卖方案。因此,如何利用区块链和智能合约保证双边云资源拍卖支付公平的问题仍有待研究。
针对上述问题,本文提出了一种公平高效的安全双边云资源拍卖方案。引入两个代理商服务器,与拍卖商服务器构成三方计算模型,三方协作运行一系列安全高效的协议来实现整个拍卖流程,在不泄露拍卖隐私的情况下,大幅提高了计算效率。具体地,本文在安全三方计算模型下设计了安全比较协议和安全排序协议,该协议通过第三方生成辅助计算参数,尽可能地减少同态加密等耗时操作的使用。在此基础上,实现了一个兼顾竞价隐私和拍卖效率的安全双边云资源拍卖方案。为了满足云资源拍卖的效率要求,采用轻量级加法秘密分享方法执行大部分安全计算功能,同时将耗时的加解密与密文域操作次数降至最低。此外,本文还考虑了云虚拟机拍卖的公平支付交易问题。由于云虚拟机交易具有高实时性要求,获胜买家拒绝付款或延迟付款都会给卖家带来经济损失。因此,本文基于智能合约对拍卖交易流程进行限定以保证交易支付的公平性。
本文主要贡献如下:1) 基于加法秘密分享采用“置乱再计算”(Shuffle-then-compute)策略设计了一种安全高效的三方安全排序协议,该协议可以作为各种安全拍卖方案的基础;2) 基于加法秘密分享和智能合约实现了公平高效的安全双边云资源拍卖方案,通过使用轻量级秘密分享方法执行大部分安全计算功能,显著提高了拍卖的性能;3) 开发实现原型系统,并通过大量实验验证了该方案的正确性和高效性。
1 系统定义
1.1 系统模型
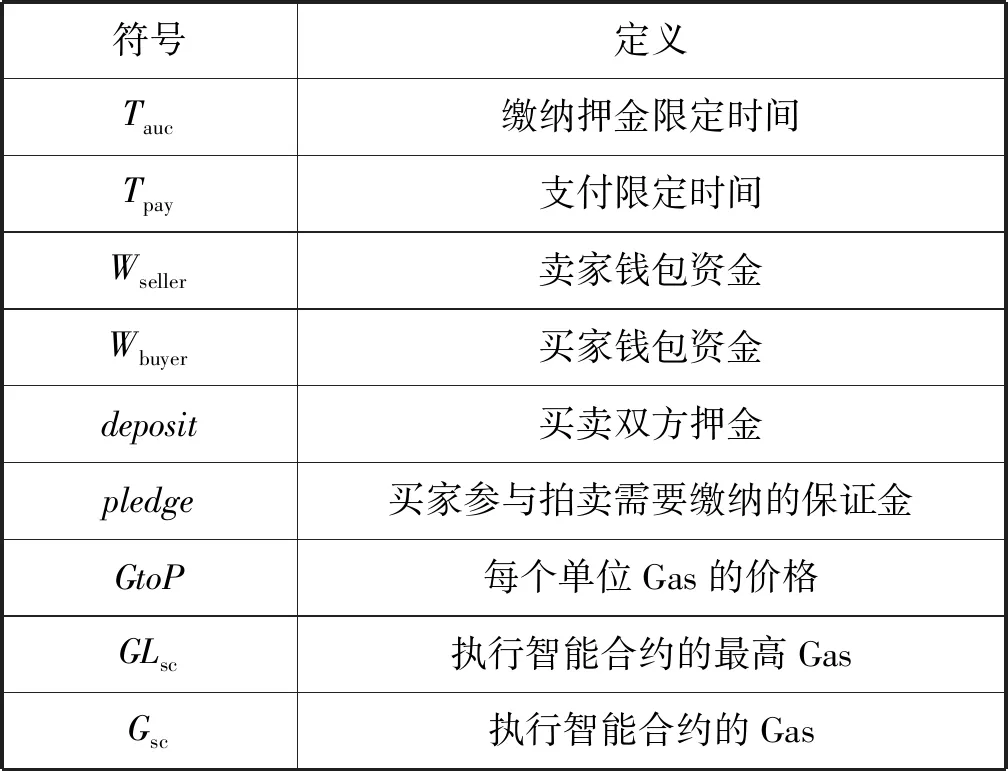
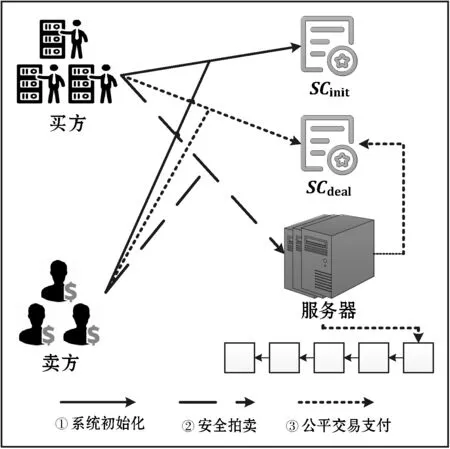
本文考虑双边市场下隐私保护的云虚拟机拍卖问题,系统模型如图1所示。参与实体包括多个买方、多个卖方、拍卖商服务器(A)、2台拍卖代理服务器(B和C)。在该模型下,M个卖方出售K种类型的虚拟机资源给N个买方。在拍卖过程中,买方和卖方在本地分别对其出价和报价进行加法秘密分享,然后将秘密分享份额分别发送至拍卖商服务器A和拍卖代理服务器B。接下来,拍卖商服务器A联合拍卖代理服务器B和C执行一系列三方安全计算协议来确定最终获胜的买方、卖方,以及相应的支付价格和资源售卖数量。最后,拍卖商服务器A调用智能合约自动完成支付交易流程。系统参数如表1所示。

图1 系统模型

表1 系统参数
1.2 安全模型及需求
本文研究半可信攻击模型下的双边云虚拟机拍卖,即所有参与方都是诚实且好奇的,这些实体将会严格执行所设计协议,但是会试图通过传输的中间消息推测其他参与方的隐私信息。此外,本文假设参与安全计算的服务器之间不会发生共谋。本文旨在设计公平的安全双边云虚拟机拍卖方案,将保证以下特性:
(1) 安全性:任一参与方均不会获得除了拍卖结果以外的隐私信息。(2) 公平性:一旦拍卖成功,在一定时限内获胜卖家可获取相应报酬,获胜买家可获取相应的资源,参与计算的代理商和代理服务器可获取相应的佣金;反之,导致流拍的参与方将会扣罚保证金。
2 背景知识
2.1 双边云虚拟机拍卖
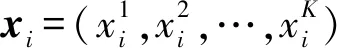
1) 胜者匹配。拍卖商首先计算每个买家的出价密度:
φi=ci/(xi·μ)
(1)
式中:公开参数μ=(μ1,μ2,…,μk)T是每种虚拟机的最大服务率。拍卖商根据出价密度对所有出价信息进行降序排序,即:
φα1≥φα2≥…≥φαN
(2)
拍卖商根据报价对不同类型虚拟机的报价信息进行升序排列,即:
(3)
接下来,拍卖商根据以下不等式来确定是否有买家和买家赢得本轮拍卖:
(4)
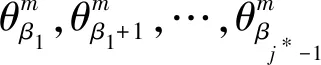
2) 定价与虚拟机分配。拍卖商计算获胜买家winb的支付金额:
(5)
获胜卖家wins对于类型m虚拟机售价为:
(6)
获胜卖家wins出售的类型m虚拟机的数量为:
(7)
拍卖商将本轮获胜的买家卖家从拍卖中移除,重复步骤1)和步骤2)直至式(6)无法成立。
2.2 安全计算原语与协议
1) 加法秘密分享[18]:加法秘密共享方通过将l位的输入值x在环Z2l上随机地拆分为2个加法秘密份额〈x〉0和〈x〉1,并分别发送给参与方A和B;对于x的秘密分享形式〈x〉,有〈x〉0+〈x〉1≡x(mod 2l)。为了恢复秘密值x(Rec(〈x〉0,〈x〉1)),A和B互换秘密份额并计算x=〈x〉0+〈x〉1。两个加法秘密分享值和求和计算定义为:参与方A和B分别在本地计算〈z〉i=〈x〉i+〈x〉i(mod 2l)(i∈{0,1})。本文余下部分将省略mod运算。
2) 安全计算协议:在之前的工作中[19-20],基于加法秘密分享提出了两种基本的安全计算协议。
(1) 安全乘法(SMUL)协议[19]:参与方A持有〈x〉0,〈y〉0∈Z2l,参与方B持有〈x〉1,〈y〉1∈Z2l,A和B在辅助计算方C的协助下计算(〈z〉0,〈z〉1)=SMul(〈x〉,〈y〉),满足〈z〉0+〈z〉1=x·y,其中:〈z〉0仅被A获取,〈z〉0仅被B获取。
(2) 安全除法(SDIV)协议[20]:参与方A持有〈x〉0,〈y〉0∈Z2l,参与方B持有〈x〉1,〈y〉1∈Z2l,A和B协同计算(〈z〉0,〈z〉1)=SDiv(〈x〉,〈y〉),满足〈z〉0+〈z〉1=x/y,其中:〈z〉0仅被A获取,〈z〉0仅被B获取。
2.3 智能合约
区块链概念源于2009年中本聪提出的比特币[21]。经过了十年的发展,区块链已经能够在金融、供应链等领域成熟应用。以太坊(Ethereum)是一个开源的具有智能合约功能的公有链平台[22]。由于图灵完备,以太坊成为应用最广泛的区块链加密货币平台。以太坊能够通过其专有的Ether和Gas提供去中心化以太虚拟机[23](Ethereum Virtual Machine,EVM)和去中心化应用(Decentralization Applications,DAPPs)来处理点对点智能合约[24](Smart Contracts)。
智能合约是以太坊相对于比特币的巨大进步。智能合约本质是跑在以太坊上的一段代码,通过分布式一致性和自动执行来保证代码运行的不可更改、不可人为操控,从而实现其安全性和不可篡改性。Solidity是以太坊为了开发智能合约专门设计的一种高级编程语言,能够良好地运行在EVM上[25]。Solidity可以实现投票、众筹、拍卖、多重签名钱包等智能合约。
3 安全计算子协议设计
根据2.1节的双边云虚拟机拍卖流程可知,比较和排序操作是拍卖过程的主要操作,因此提出两种安全三方计算协议来实现安全高效的比较与排序操作。以下协议均在1.1节描述的安全三方计算模型下进行,并假设参与方A拥有加法同态密码公私钥pk/sk,其他参与方拥有公钥pk。
3.1 安全比较协议
给定两组加法秘密分享值〈x〉i、〈y〉i(i∈{0,1}),其中:〈x〉0、〈y〉0存储在A上,〈x〉1、〈y〉1存储在B上。安全比较(SCMP)协议的功能是在半可信的第三方C的辅助下根据x和y的大小关系输出z的秘密分享份额〈z〉i,其中z=(x≥y),〈z〉0仅被A获取,〈z〉1仅被B获取。在协议的整个过程中,没有关于x和y的任何隐私信息泄露给A和B。SComp协议基本原理如下:
(x-y)r≥0⟹(x≥y)
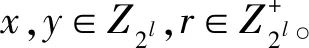
协议1安全比较SComp协议
输入:A输入〈x〉0,〈y〉0,B输入〈x〉1,〈y〉1。
输出:A输出〈z〉0,B输出〈z〉1,z=(x≥y)。
1) A和B分别生成随机正整数〈r〉0∈Z2l和〈r〉1∈Z2l,C生成1和0的加法秘密分享份额〈u〉i=〈1〉i和〈v〉i=〈0〉i,i∈{0,1};
2) A计算〈e〉0=〈x〉0-〈y〉0,B计算〈e〉1=〈x〉1-〈y〉1,A和B在C的辅助下使用SMul协议计算〈f〉=SMul(〈e〉,〈r〉);
3) A和B将f的加法秘密份额发送给C,C在本地恢复出f的值f=Rec(〈f〉0,〈f〉1);
4) 如果f≥0,〈z〉i=〈u〉i,否则〈z〉i=〈v〉i,i∈{0,1},C将〈z〉0和〈z〉1分别发送给A和B。
3.2 安全排序协议
给定一组加法秘密分享形式的序列〈x〉=〈〈x1〉,〈x2〉,…,〈xn〉〉,其中:x0、x1分别存储在A和B上,安全排序(SST)协议的功能是在C的辅助下将原序列排列成一组加法秘密分享形式的递增序列〈xφ〉=〈〈xφ(1)〉,〈xφ(2)〉,…,〈xφ(n)〉〉,其中φ是原序列索引与递增序列索引之间的映射。在协议的整个过程中,没有关于x的任何隐私信息泄露给A和B。
为了在加法秘密分享的形式上实现安全高效的排序操作,本文采用了“置乱再计算”的策略设计安全排序协议。具体地,在常规排序操作之前添加一个数据置乱操作用来切断置乱后的序列与原序列的关系,后续对置乱序列的操作则不会泄露原序列元素间大小关系、访问模式等隐私信息。协议2描述了安全排序协议的流程。
协议2安全排序(SST)协议
1) A和B分别生成随机序列u=[u1,u2,…,un],然后A对u进行加法同态加密得到L0=[Epk(u1),Epk(u2),…,Epk(un)],并发送给C;B以同样的方式得到加密随机序列L1=[Epk(v1),Epk(v2),…,Epk(vn)]发送给C。
2) C接收到L0和L1后,计算L2=〈Epk(u1)·Epk(v1),Epk(u2)·Epk(v2),…,Epk(un)·Epk(vn)〉=〈Epk(u1+v1),Epk(u2+v2),…,Epk(un+vn)〉,使用置乱函数π对L2中元素进行置乱操作得到L2=〈Epk(uπ(1)+vπ(1)),Epk(uπ(2)+vπ(2)),…,Epk(uπ(n)+vπ(n))〉并发送给A。
3) A使用私钥sk对L2解密并取反得到一组序列,记作〈x′〉0=[-uπ(1)-vπ(1),…,-uπ(1)-vπ(1)]。
4) A计算L3=〈〈x1〉0+u1,〈x2〉0+u2,…,〈xn〉0+un〉并发送给C;B计算L4=〈〈x1〉1+v1,〈x2〉1+v2,…,〈xn〉1+vn〉并发送给C。
5) C计算L3+L4并使用π对其进行置乱操作得到〈x′〉1=〈xπ(1)+uπ(1)+vπ(1),xπ(2)+uπ(2)+vπ(2),…,xπ(n)+uπ(n)+vπ(n)〉并发送给B。
6) A和B设置low=1,up=n
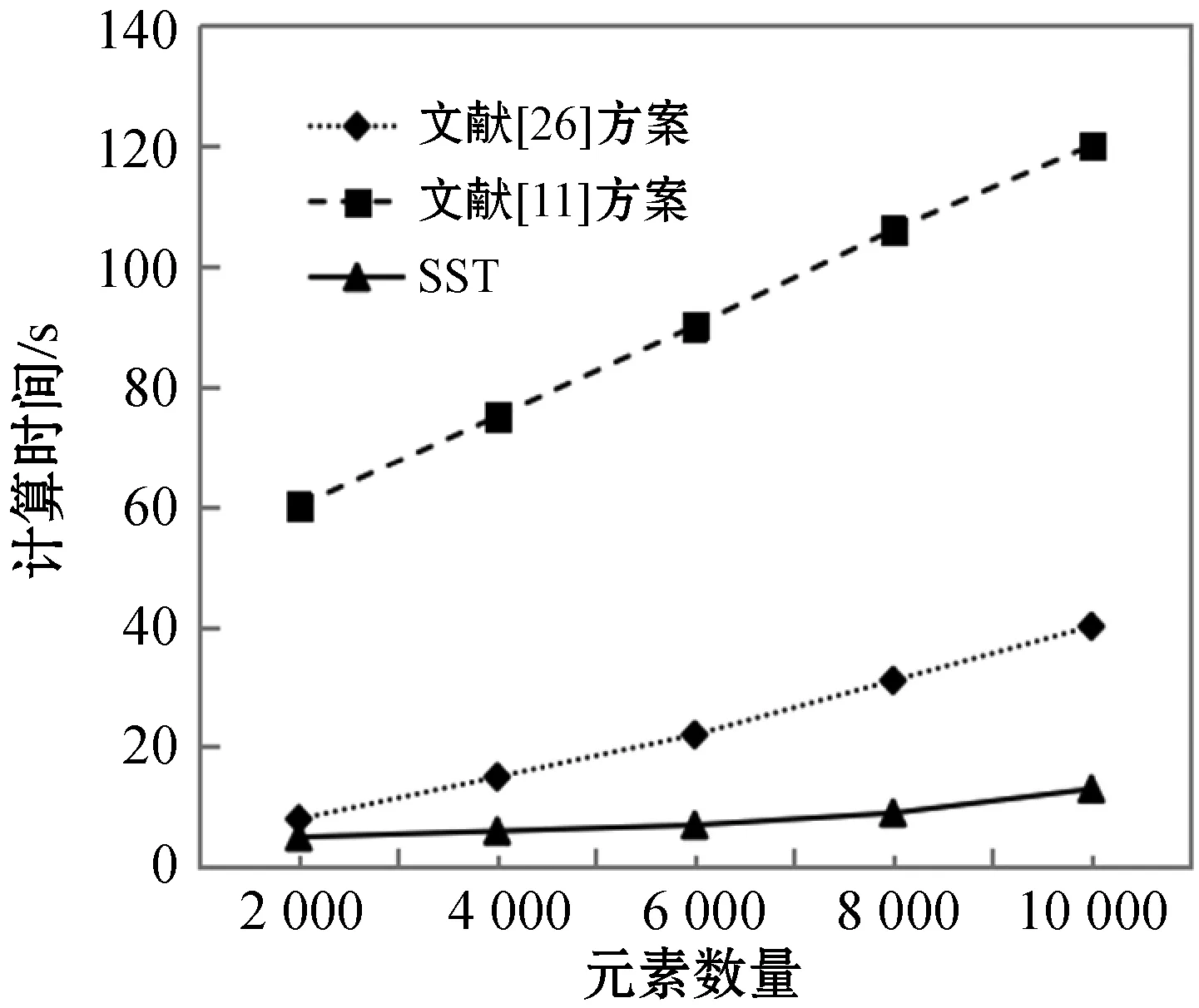
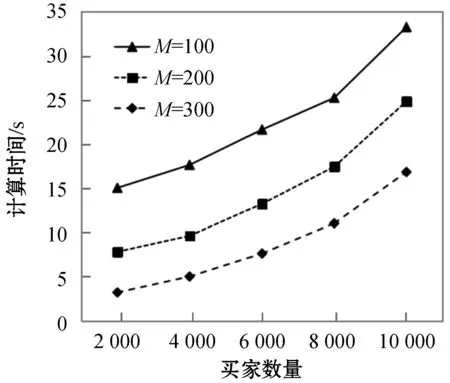
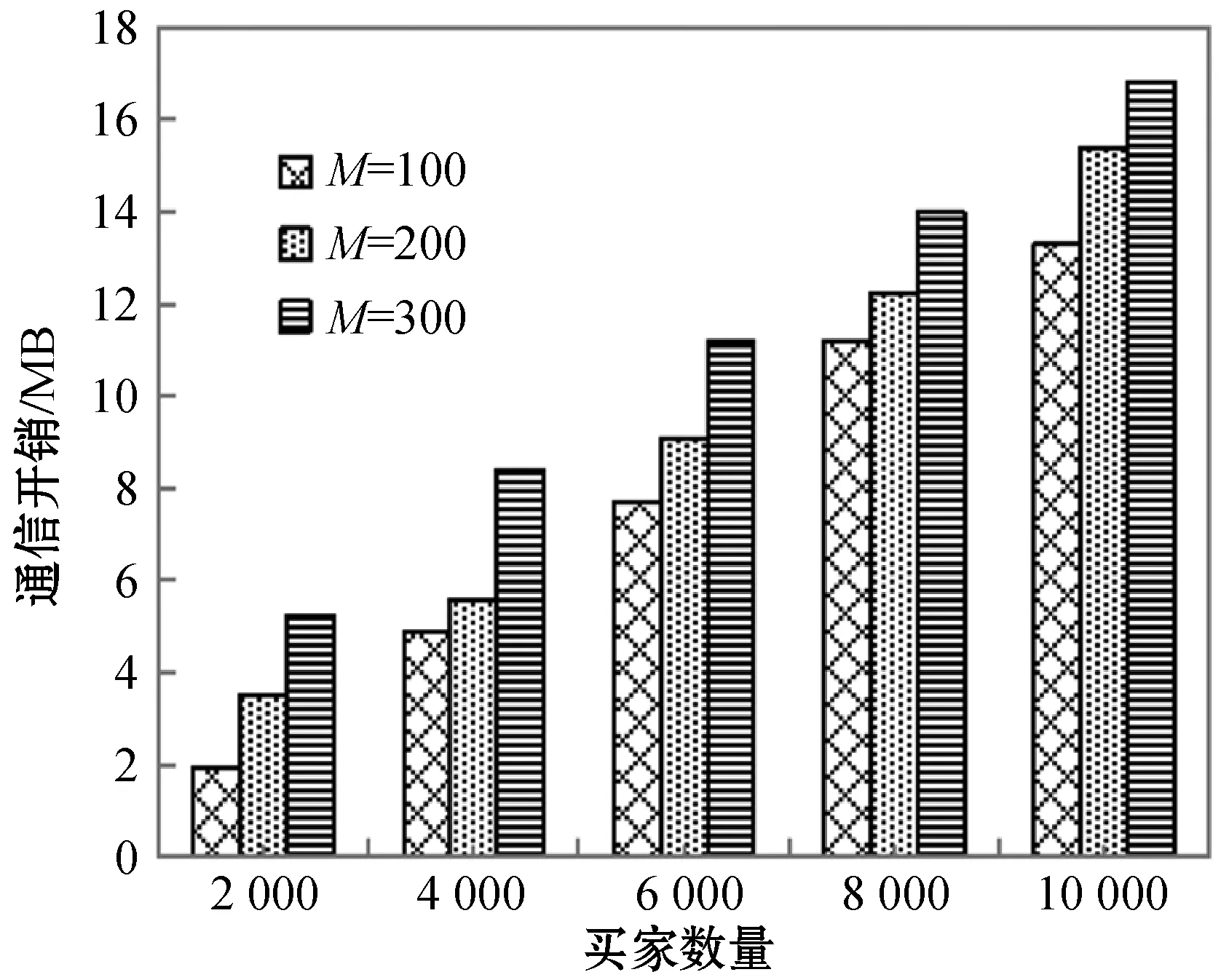
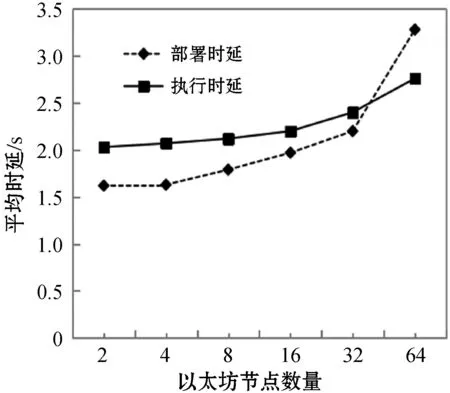
7) iflow 10) forj=lowto (up-1) 14) end if 15) end for 17) A和B设置up=i-1,重复步骤7)至19) 18) A和B设置low=i+1,重复步骤7)至19) 19) end if 20) A设置〈xφ〉0=〈x′〉0,B设置〈xφ〉1=〈x′〉1 具体地,A和B生成随机序列u=〈u1,u2,…,un〉和v=〈v1,v2,…,vn〉,使用加法同态加密后发给C。C在本地利用加法同态性质计算得到L2=〈Epk(u1+v1),Epk(u2+v2),…,Epk(un+vn)〉,使用置乱函数π对L2中元素进行置乱操作并将置乱后的序列发送给A。 A使用私钥sk对L2解密并取反得到〈x′〉0=[-uπ(1)-vπ(1),…,-uπ(1)-vπ(1)]。接下来,A和B分别使用u、v对〈x〉0、〈x〉1进行混淆并发送给C,C计算混淆后序列的和并使用π对其进行置乱操作得到〈x′〉1=[xπ(1)+uπ(1)+vπ(1),xπ(2)+uπ(2)+vπ(2),…,xπ(n)+uπ(n)+vπ(n)],然后将〈x′〉1发送给B。至此,A和B上存储着置乱后序列的加法秘密分享值。接下来,以〈x′〉为输入,进行快速排序操作。与传统的快速排序算法相比,本文采用SCMP协议完成加法秘密共享数据上的安全比较操作。由于采用了上述方法,该协议可以很容易地扩展,以支持键值对类型数据的安全排序,即数组中的元素是键值(ki,xi),xi用于对数组进行排序。 基于上述安全计算协议和智能合约,提出了一种公平的安全双边云虚拟机拍卖方案,旨在解决拍卖过程可能出现的隐私泄露和公平交易的问题。本节智能合约中相关符号及定义如表2所示。如上文所述,本文安全拍卖协议基于3.1节所介绍的拍卖协议构建,包括系统初始化、安全拍卖和交易支付三个阶段,如图2所示。 表2 智能合约相关符号 图2 公平的安全双边云虚拟机拍卖方案执行流程 1) 卖家向区块链注册拍卖品 2) 卖家设置拍卖保证金额度 3) 卖家设置最长拍卖时间Tauc 4) 卖家设置最长支付时间Tpay 5) 卖家缴纳手续费depositrseller 6) 买家缴纳保证金和手续费depositbuyer 7) 验证:押金缴纳时间T′ deposit=depositrseller+depositbuyer depositrseller>(Lsc×GtoP)/2 depositbuyer>(Lsc×GtoP)/2+pledge (a) 账户配置交易(b) 卖方押金交易 (c) 买方押金交易 (d) 胜方支付交易图3 区块链交易结构 2) 拍卖执行:当收到报价的秘密份额后,A与B将执行安全拍卖协议来完成胜者匹配、定价与虚拟机分配,主要步骤如协议3所示。 协议3隐私保护拍卖协议 输入:A和B中所有秘密分享的报价。 输出:秘密分享形式的拍卖结果。 1)for1≤i≤N 2)for1≤m≤K 4)endfor 6)endfor 12)for1≤m≤K 14)endfor 15)A,B,C: 17)for1≤j≤M 19) 〈λj〉←SCMP(〈φ〉,〈δj〉) 23)endfor 24)for1≤j≤M-1 25) 〈ηj〉←〈λj〉-〈Vα1〉 26)endfor 27) 〈ηM〉←〈λM〉 28) 〈j*〉←〈η1〉×〈1〉+〈η2〉×〈2〉+…+〈ηM〉×〈M〉 30)for1≤m≤K 32)endfor λj数组用于表示j是否小于或者等于关键索引j*,当j小于等于j*时,λj=1;否则,λj=0。 ηj数组用于表示j是否等于关键索引j*,当j等于j*时,ηj=1;否则,ηj=0。 为了帮助理解这一设计,下面给出关键索引和两个标识数组的具体形式: 2) 退还非获胜买家的保证金,即发送pledge给Wbuyer 3) 获胜买家实际支付金额cost1 6) 更改cost2的所有权给Wseller 7) 更改拍卖资源所有权给Wbuyer 8)differ=cost1-cost2 9) 发送differ给服务器WA 10) 退还获胜者的保证金,即发送pledge给Wbuyer 11) end if 13) 更改获胜者押金的所有权给Wseller 14) end if 15) 发送手续费Lsc×GtoP给服务器WA、WB、WC 本节将对安全计算子协议、安全拍卖协议和公平交易智能合约进行性能评估。本文实验环境为Intel(R) Core(TM) i7-4790U CPU@3.60 GHz,8 GB RAM配置的64位计算机。对于安全计算协议部分,使用C++实现,平均网络延迟0.04 ms。对于智能合约部分,在本地服务器上搭建以太坊测试网络,利用多台EVM模拟多个以太坊节点。在该网络中,使用Solidity 0.4.24版本进行智能合约开发。本节对智能合约的性能分析主要针对的是以太坊私有测试网络,其原因是私有网络上参与的区块链节点是可控的,部署的智能合约是可分析的。这既符合拍卖场景,又便于实验分析。同时,由于拍卖过程不会产生大量需要记录上链的交易和区块,因此本节不考虑世界状态(World State)对以太坊智能合约调用的影响。 从安全拍卖方案具体步骤可以看出,安全排序是整个拍卖过程中最为重要且最费时的操作。图4展示了安全排序(SST)协议和其他两种基于同态加密[26]和混合式加密[11]解决方案的性能比较。可以看出,随着元素数量增加,SST协议计算时间呈对数增长,而另外两种方案接近线性增长。SST协议相较之前两种方案具有显著性能优势,这是因为使用了轻量级的加法秘密共享方法执行了大部分安全计算操作,并且由于第三方辅助服务器的存在,极大地减少了同态加解密与密文域操作的次数。 图4 安全排序(SST)协议计算时间对比 图5和图6分别显示了在一轮拍卖过程中不同数量的卖家M和买家N情况下安全拍卖协议的计算时间和通信开销。对于不同数量的买家M,计算时间均随着卖家数量N的增加以近似线性的速度增加,这与排序协议中相似。对于通信开销,可以在图6中看到相同的趋势,这是因为排序操作的开销占了整个拍卖开销的绝大部分。 图5 不同买家卖家数量时的安全拍卖协议计算时间 图6 不同买家卖家数量时的安全拍卖协议通信开销 主要分析以太坊节点数量与拍卖智能合约部署和调用时延之间的关联关系,如图7所示。首先分析智能合约的部署时延,即在初始化时为每个区块链节点安装、配置智能合约的平均时间,如图7实线所示。智能合约的部署时延与节点数量线性相关,随节点数量的增加而增加。智能合约的执行时延,即执行合约中输入/输出功能的平均时间,如图7虚线所示。智能合约的执行时延随节点数量的增加而增加,但增幅极小。这是由于大多数以太坊节点只有在保证金缴纳和退还阶段调用智能合约,获胜者支付阶段只有买卖双方参与智能合约的执行。 图7 不同节点数量时的智能合约时延 针对云资源拍卖过程中隐私泄露和公平支付问题,本文基于加法秘密分享提出安全比较和安全排序协议,并基于此设计了一种公平高效的安全双边云资源拍卖方案。通过采用置乱再计算的设计策略和第三方代理服务器的辅助,大幅提升了协议的计算和通信效率。此外,本文利用智能合约保证了拍卖过程中公平的交易支付。通过实验对比分析,本文方案相较于之前的工作在拍卖计算时间和通信开销方面均具有显著优势。在未来工作中,将继续研究支持各种拍卖算法的安全协议,进一步提升协议的安全性。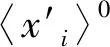
4 安全双边云虚拟机拍卖
4.1 安全排序协议





4.2 安全拍卖
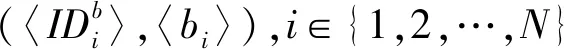
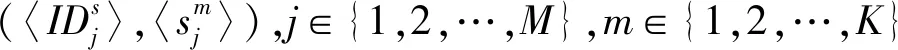
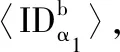
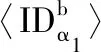
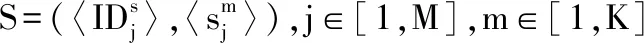
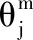
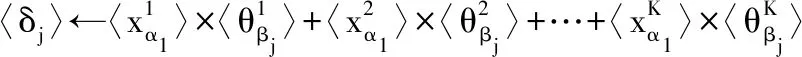
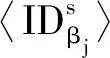


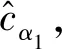
4.3 公平交易支付



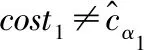
5 性能评估
5.1 安全计算协议性能
5.2 智能合约性能
6 结 语
