基于HMM的电动出租汽车行驶状态预测改进模型研究

唐 飞 刘大明 郭傅傲

(上海电力大学计算机科学与技术学院 上海 200092)

0 引 言

“互联网+交通”模式产生一系列新兴业态，对人们的城市交通出行方式带来颠覆性的改变。仅2014年一年我国中心城市出租汽车载客车次总数就达到657 467万次，运营里程6 204 401万公里，预计新增电动出租汽车12.1万辆，电动出租汽车发展迅猛。相对于传统化石能源，电力无法大规模储能，电动出租汽车的入网，将对电网安全运行和优化调度造成困难。建立有效的电动汽车行驶状态预测模型，为分析电动出租汽车行驶特征和充电负荷预测打下基础，从而优化电动出租汽车调度控制[1-4]。当前可用的电动出租汽车行驶数据极少，相对而言，随着定位技术的成熟与发展，出租汽车行业已经累积了大量用户位置数据。电动出租汽车属于一类特殊的出租汽车，二者拥有相似的经营特点[5]，且司机的驾驶习惯极少由于驾驶电动出租汽车而改变[6]，可以使用普通出租汽车数据对电动出租汽车进行研究。

车辆行驶状态具有空间和时间规律性，具有预测的可能性。文献[7]通过观察记录252位司机40天的行程发现，大约60%的司机会选择具有相同时间、位置特征的行程，即倾向于每天进行相同的出行。文献[8]通过跟踪100 000条手机行动轨迹六个月的数据指出：人类轨迹显示出高度的时间和空间规律性，每个个体都大概率往返于几个高频率坐标位置，遵循简单的可再现模式。

在行驶状态预测模型中，马尔可夫模型对于离散的时间与状态具有良好的时序性，目前对于GPS轨迹数据的研究主要基于马尔可夫模型进行建模预测。文献[9-10]通过聚类方法对GPS数据中的重要位置进行数据挖掘，并将其合并到马尔可夫模型中进行目的地预测。文献[11]使用连续路线模式挖掘从GPS轨迹数据中提取历史运动模式，从而对未来运动模式进行预测。文献[12]通过高斯混合模型对移动对象运动模式的概率分布进行计算，将GPS轨迹数据划分为不同分量，从而预测未来轨迹。文献[13]将轨迹信息作为观测状态，实际路网信息作为隐状态，建立隐马尔可夫模型进行汽车位置预测。

分析现有的出租汽车路径预测相关研究工作，主要集中在出租汽车轨迹数据挖掘[14-17]、出租汽车的交通情况估计[18-20]和出租汽车运营管理[21-23]三部分，针对电动出租汽车的研究较少。出租汽车相对于私家车有目的地随机性大、路径选择多、停留时间短等特点，需要采用适应出租汽车出行习惯的建模策略。文献[24]使用滑动窗口模型估计轨迹未来轨迹范围，从而获取候选轨迹列表并建立模型进行位置预测，能较好地表示出租汽车无序的路径选择，但其采用的一阶马尔可夫模型仅使用当前位置进行预测，对历史轨迹利用不充分，预测精度较低。针对上述问题，本文提出使用滑动窗口的隐马尔可夫模型电动出租汽车行驶状态预测方法。该方法首先通过载客状态与行驶距离对轨迹信息进行划分，然后建立隐马尔可夫模型，通过适应电动出租汽车行驶特点的改进解法求解相关参数。

1 行驶状态识别

为了对电动出租汽车行驶状态进行预测，需要根据出租汽车相对普通私家车的特殊行驶模式对GPS轨迹数据中包含的信息进行提取。GPS轨迹数据一般由一系列以时间为序的点组成，每个点包含坐标及行驶相关信息。为了利用这些信息，需要进行出租汽车状态识别，即从轨迹数据中识别出目的地坐标，将整段行驶路径划分为若干行程。

出租汽车的行驶行为与普通私家车存在很大区别：相对于私家车，出租汽车没有既定的目的地，其目的地通常由乘客决定，这使出租汽车一天的行程相对私家车更无序；出租汽车更多是为了接客而进行短期停留，而不是像私家车那样在工作场所或商场周边停留几小时。因此，本文做如下定义：

定义1目的地。出租汽车进行停留或者下客的地方定义为目的地dn。

定义2行程。两个目的地之间的行驶轨迹定义为行程ln。去往同一个地点通常有多条可选路线，即相同的两个目的地之间存在多段可能的行程。

定义3行驶状态。通过定义1与定义2中的目的地与行程将GPS轨迹划分成k个包含目的地与路径轨迹的行驶状态，单个行驶状态表示为sn={ln,dn}，1≤n≤k。

定义4载客状态。将出租车载客状态记作αi，载客记为1，空载记为0，有乘客上下车即记作载客状态发生变化。

根据上述定义，为了识别出行驶状态，使用出租汽车载客状态与停留动作从GPS轨迹中提取出目的地dn组成目的地集合STAY。首先根据定义4中的载客状态αi的变化进行判断。载客状态能够清楚地反映出何时出租汽车将乘客送到目的地及何时何地出租汽车接到新乘客结束空载状态。若是判断到αi发生改变，就将发生状态改变的坐标Li存入目的地集合STAY。

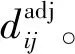
(1)

式中：Lng代表经度；Lat代表纬度；R代表地球半径，取值为6 317 km。

定义5停止持续时间。出租汽车能被判断为在坐标Li进行停留的最小停留时间记作tdur，本文定义tdur=5 min。

定义6漫游距离。出租汽车能被判断为在坐标Li进行停留的最大偏移距离记作漫游距离，即在tdur时间内所有dadj的和，其计算如下：

(2)

划分后的部分坐标轨迹如图1所示，其中共有四个目的地，两个目的地之间的坐标被划为两段载客行程和一段空载行程。

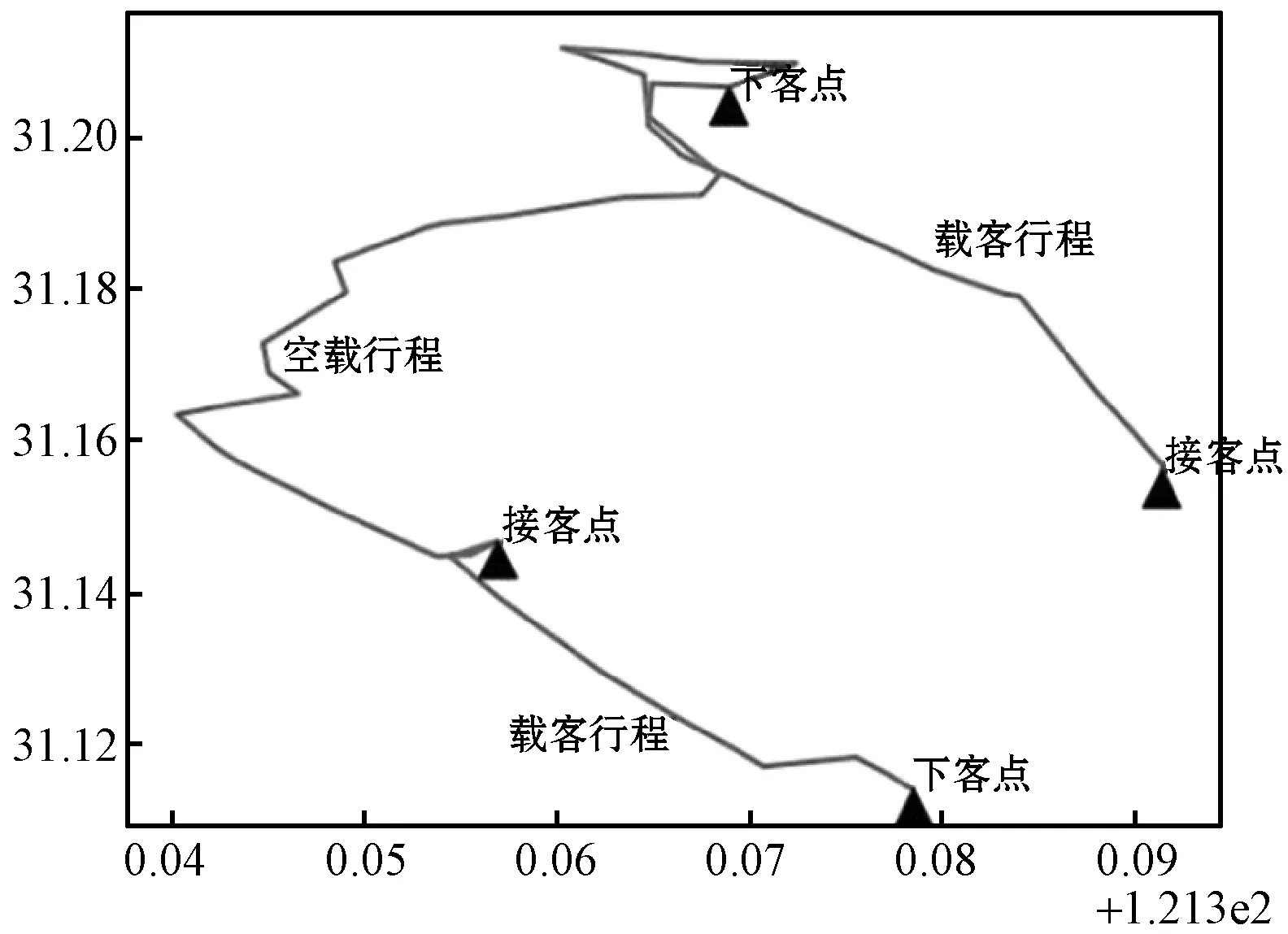
图1 轨迹划分举例

2 预测方法

在对轨迹信息进行处理之后，对出租汽车的旅行中的行程进行预测，即预测出租汽车行驶的下一个状态sn。使用隐马尔可夫模型进行预测，使用滑动窗口模型改进状态转移概率求解，Baum-Welch算法用以求解观察概率与初始概率分布。

2.1 隐马尔可夫模型

隐马尔可夫模型(Hidden Markov Model，HMM)最初由一些学者发表在一系列的统计学论文中。马尔可夫模型在出租汽车行驶状态预测中可以很好地表示时序位置关系，能很好地应用于位置建模和预测；而隐状态的加入使HMM成为一个双重随机过程，可以充分考虑到坐标与现实道路不匹配的问题。因此，本文选择使用HMM对出租汽车行驶状态进行预测。

定义7隐马尔可夫行驶状态预测模型。HMM是一种含有隐状态的马尔可夫过程，为了应用于行驶状态预测，模型包含五个基本要素，可表示为一个五元组λ=(S,O,A,Z,π)，其中：

(1)S表示一组状态，且S=(s1,s2,…,sN)，N是状态的总数，一般来说S中的是不可观测的隐状态。

(2)O表示一组观察值O=(o1,o2,…,oM)，M是观察值的总数，一般来说O中的观测值是可以从数据中直接得到的。

(3)A={aij}是状态转移概率，且aij=p(sj|si)，表示从si状态转移到sj状态的概率。

(4)Z={zi}是观察概率，且zi=p(oi|si)，表示系统在si状态被观测到观测值oi的概率。

(5)π={πi}是隐藏状态的初始概率分布，πi表示当时间t=1时状态si的概率分布。

si状态在t时间的概率分布记作pt(si)，当t=1时p1(si)=π是si状态的初始概率分布。sj状态在t+1时间的概率分布可以通过下式计算得到：

(3)

为了更新概率分布，可以使用贝叶斯准则[28]获得：

(4)

(5)

式中：p(ot+1)作为归一化因子。

为了进行路径预测，需要将出租汽车行驶的元素与HMM的基本元素进行匹配。隐状态集S由第一节中得到的s={l,d}组成，代表由一条路线l到达目的地d的状态。因此，状态转移概率aij=p(sj|si)也对应代表着出租汽车从si状态转移到sj状态的概率。观察集O对应出租汽车的瞬时坐标，可以直接从GPS轨迹中得到。观察概率Z表示GPS位置与实际路网的匹配程度，对应为zi=p(oi|si)，即当出租汽车处在si状态时被观测到GPS坐标为oi的概率。

2.2 状态转移概率计算

2.1节中完成了对HMM基本元素的定义，隐状态集S与观察集O都能通过轨迹数据得到，剩下的任务就是计算状态转移矩阵A，观察矩阵Z以及初始状态π。由于出租汽车单次行程距离短，目的地变化快，本文采用文献[24]提到的滑动窗口模型改进HMM状态转移概率计算。

定义8滑动窗口模型。滑动窗口模型根据出租汽车实时位置建立半径为Rd的圆形滑动窗口，通过统计历史行程数据预测未来最有可能选择的行程，从而预测出租汽车的未来位置。

其中半径Rd=vave·Tp，vave是车辆行驶速度，Tp表示预测周期。采用城市路网的平均速度作为车辆行驶速度，即vave=40 km/h，用GPS轨迹数据采集周期作为预测周期Tp，对滑动窗口的半径Rd进行计算。

滑动窗口模型如图2所示，表示在局部道路网络使用滑动窗口进行状态预测。其中虚线圆圈就是一个动态窗口，l是供选择的行程，d是行程的目的地。圈中所有的行程l都是未来的可选行程。

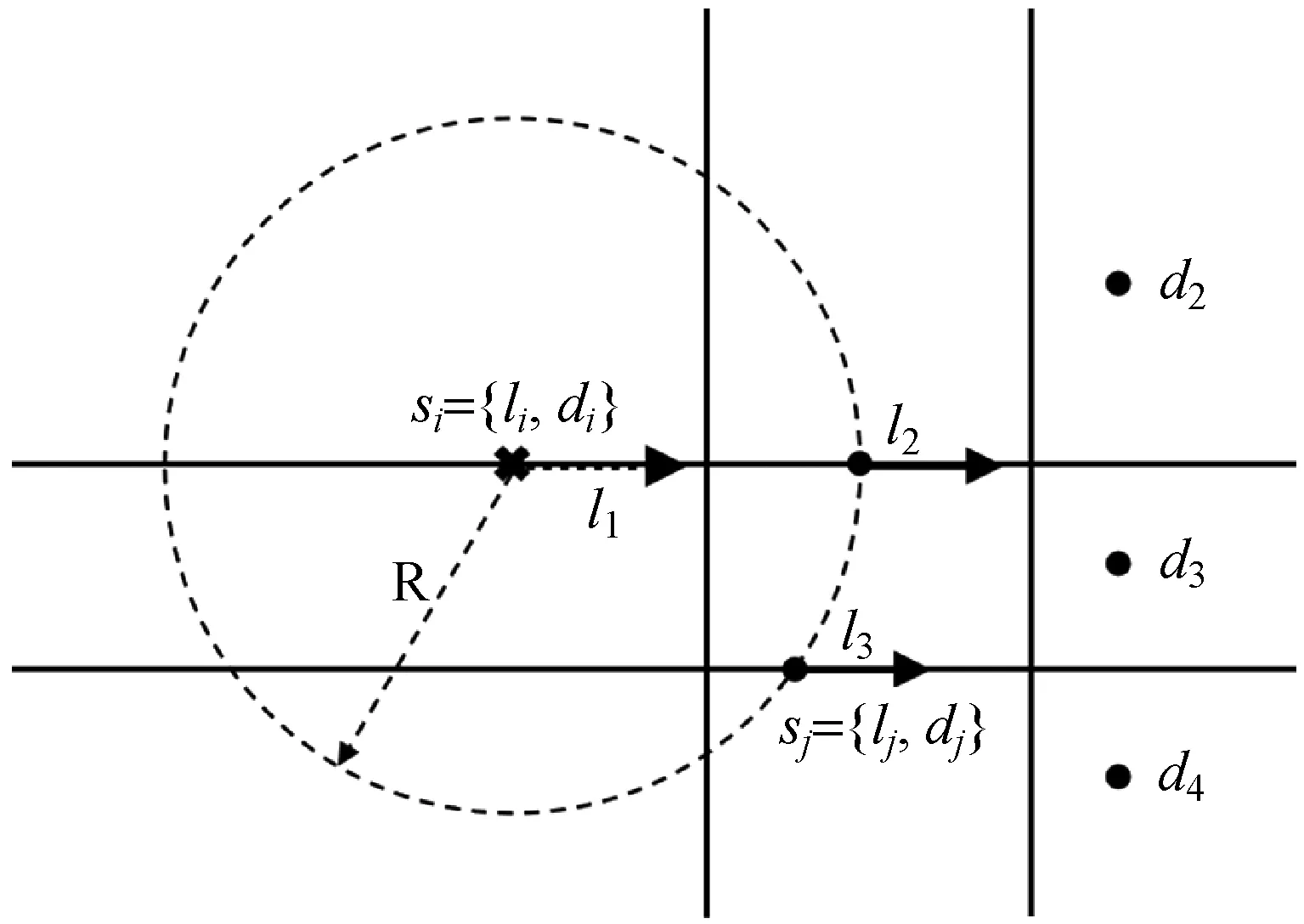
图2 滑动窗口模型

为了降低模型的复杂度，本文进行如下假设：(1) 假设出租汽车不会掉头返回上个行驶过的路口；(2) 假设行程l与目的地d相互独立。因此状态转移概率aij的计算式可以写作p({lj,dj}|si)=p(dj|lj)·p(lj|si)，其中p(lj|si)表示在当前状态si选择的下个行程是lj的概率，p(dj|lj)表示通过行程lj，驶向目的地dj的概率。为了计算p(lj|si)与p(dj|lj)，引入m1与m2两个参数，用图2中的道路情况举例计算过程。首先计算p(lj|si)。定义集合{lj,di,m2}，表示当出租汽车通过行程li到达目的地di后行驶入行程lj的总次数。由此可以计算：

(6)

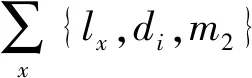
使用类似的方法，可以计算p(dj|lj)。定义集合{dj,lj,m1}，表示当目的地为dj时，出租汽车经过行程lj共m1次。由此计算：

(7)

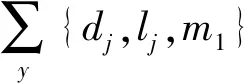
在通过aij=p(dj|lj)·p(lj|si)计算出状态转移概率aij后，可以计算下一个时间段的状态转移概率：

(8)

用式(2)和式(3)更新pt+1(sj)：

(9)

其中：

(10)

在式(8)、式(9)和式(10)中：t是状态si所在的时间段，t+1表示状态转移到下一个状态sj的时间段；ot+1表示在t+1时间段，即处在状态sj时的观察值；sk表示出租汽车从si状态向目的地dj行驶所选择的行程lk，k=1,2,…,n，n由实际道路情况确定。例如车辆处在十字路口时，n的值为3，即可选道路有3条。

2.3 Baum-Welch算法

2.2节介绍了通过滑动窗口模型改进HMM状态转移矩阵A的计算。本节将在此基础上对观察概率Z与初始状态π进行求解，随后通过迭代对三个参数进行更新。采用的方法对应概率论中的极大似估计问题。由于HMM模型包含隐状态，无法通过直接求导进行求解，故采用Baum-Welch算法[29]进行求解。

首先进行初始化，随机给观察概率zj与初始状态πi进行赋值，使其满足如下条件：

(11)

(12)

定义9前向概率。前向概率为时刻t的观察序列为(o1,o2,…,ot)，且时刻t隐状态为si的概率，记为：

αt(i)=p(o1,o2,…,ot,xt=si|λ)

(13)

在得到了前向概率后，便能利用式(14)-式(15)递归地求解前向概率和观测序列的概率：

α1(i)=πizi(1)

(14)

(15)

定义10后向概率。后向概率为时刻t隐状态为si且时刻t+1到T为止的观察序列为(ot+1,ot+2,…,oT)的概率，记为：

βt(i)=1

(16)

(17)

由于后向概率的方向是相反的，最终时刻T之后的概率不作考虑，故赋值1。

使用求得的α与β对中间变量进行计算：

(18)

然后使用求得的中间变量γ求解观察概率Z：

(19)

πi=γ1(i)

(20)

式(19)中的I(ot=ok)仅当时刻t的观察值为ok时才取值为1，否则为0。使用aij、zj与πi的更新值执行上述过程进行迭代，将最终收敛的结果作为求得的状态转移概率A、观察概率Z与初始状态π。

3 实 验

本文实验环境为Intel(R) Core(TM) i5-7300HQ CPU @ 2.50 GHz，内存8 GB。实验程序用Python编写，在Windows 10系统下运行。

实验采用的GPS轨迹数据来自香港科技大学计算机科学与工程系的手机轨迹研究项目[25]，包含在2007年2月23日上海4 316辆出租汽车一天的轨迹数据。该数据集包含了超过600万个坐标点，轨迹的总距离达到160多万公里。每辆车的数据都由m个轨迹点构成，单个轨迹点的结构为(ID,ti,Li,vi,θi，αi)，1≤i≤m。

每个轨迹点有七个字段，其中第一个字段是出租汽车的标识ID；第二个字段ti是该轨迹点的时间戳，记录轨迹点时间间隔为1分钟；第三和第四个字段Li=(Lngi,Lati)为坐标点，Lngi为经度，Lati为纬度；第五个字段vi是此时出租汽车的瞬时速度；第六个字段θi是从北方顺时针方向以2度为单位的角度，例如“157”表示出租汽车瞬时速度在顺时针方向上与北方成314度；最后一个字段αi表示载客状态。

根据数据中的经纬度极限，设定研究区域经度范围从121.075 00到121.975 00，纬度范围从30.690 00到31.790 00。为了简化预测过程，将研究区域划分成900×1 100个单元格，其中每个单元格是0.001×0.001的区域。将同一单元格中的所有坐标记作同一位置。

本文使用相对准确度RA来对预测性能进行评估，定义如下：

(21)

(22)

式中：Eave是距离平均误差；Lpre与Lact分别是预测坐标与实际坐标；n是测试样本数量；Rd是圆形滑动窗口的半径。

定义11市中心行程。根据上海内环高架将经度121.414 0～121.576 0、纬度31.205 0～31.282 0的区域定义为市中心区域，所有轨迹点都在这个范围内的行程记作市中心行程。

在验证模型准确性的过程中，为了简化验证过程，随机从所有行程中抽取十段载客行程、十段空载行程、五段市中心的载客行程、五段市中心的空载行程来作为测试样本。图3显示了载客行程、空载行程与市中心行程的预测结果。分析柱状图得出结论：(1) 对于行程预测的准确度远小于对于出租汽车目的地的预测；(2) 在市中心行程预测准确率普遍更低；(3) 空载行程的预测准确率略高于载客行程。

图3 坐标预测结果

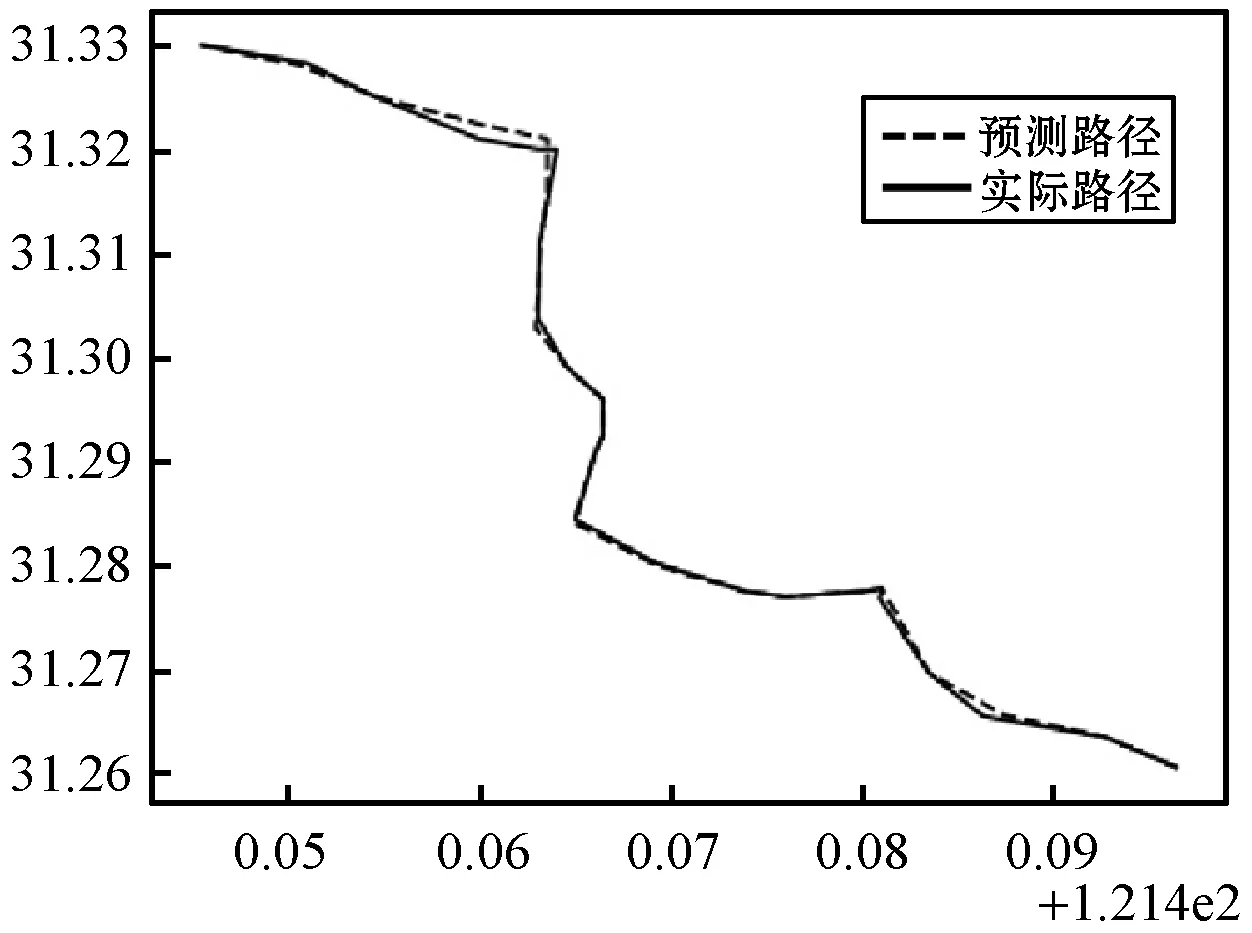
对产生的三个结论进行分析：对于结论(1)，行程预测不准确的主要原因是同一目的地多条可选路径的存在。这同时也解释了结论(2)，市中心道路更密集，可选道路也更多，也就造成了更低的预测准确率。本文选取了测试行程中RA值最低的一段绘制轨迹图如图4(b)所示，对比预测较准确的图4(a)而言，除了由于区域划分产生的误差外，图4(b)选择了与实际情况有相同目的地的另一条行程，这导致了RA值出现大量偏差。对于结论(3)，可能是出租汽车在没有载客时，司机更少进行高速行驶，行程的路程也相对更短。本文对出租汽车轨迹数据中的θi也就是角度变化进行比较后发现在空载时，出租汽车的行驶角度θi变化率更低，即空载时出租汽车更少进行急转弯，这可能也是出现空载预测更准确的原因。

(a)

(b)图4 行驶路线

另外，还对出租汽车预测轨迹的行驶里程Dmov进行了计算：

(23)

本文从所有行程中抽取了十段行程进行了行驶里程计算，并与预测结果进行了比对，结果如表1所示。

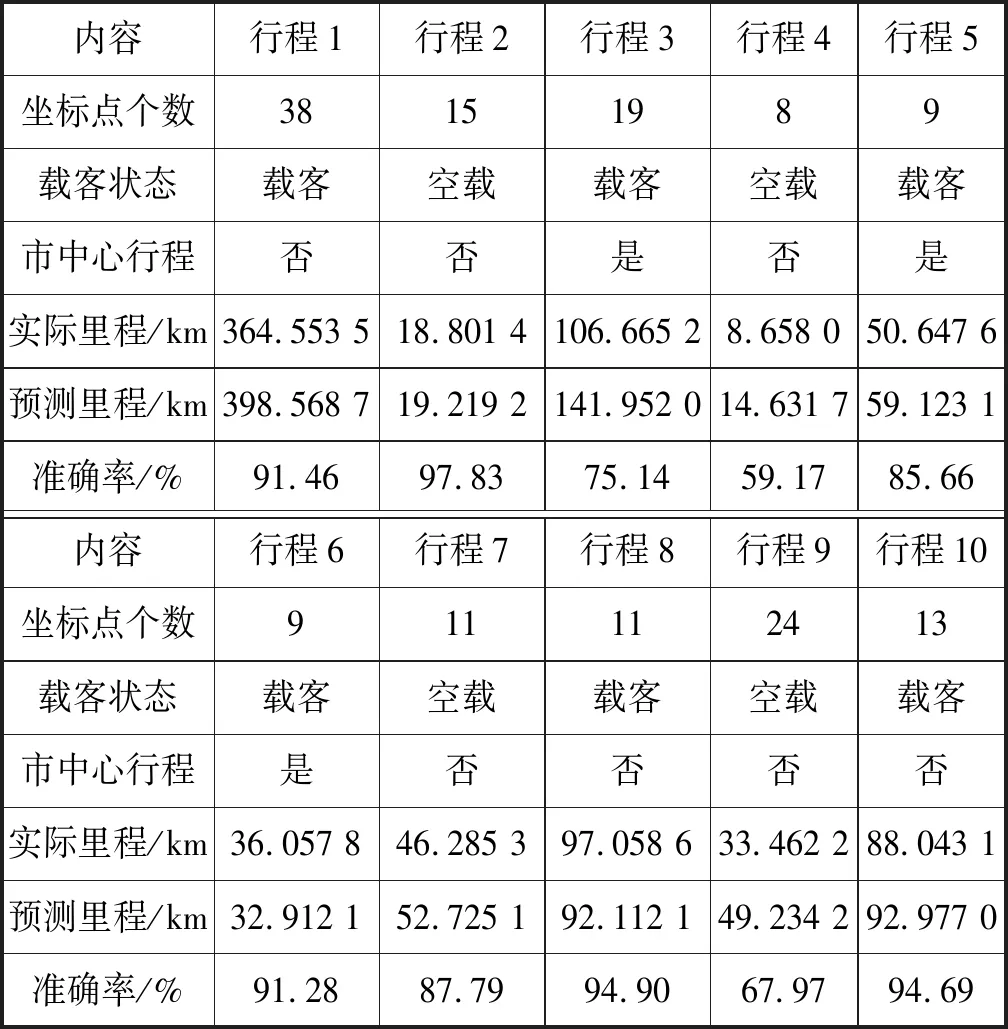
表1 预测结果

通过表1，不难发现HMM对行程的行驶里程计算相当准确，达到了84.59%。表中几个空载行程误差较大，且多是预测路程大于实际路程，原因可能是空载时，行驶速度缓慢，660 m的滑动窗口距离过大造成的。较高的目的地预测精度与行驶里程预测精度证明了本文所提出的基于HMM预测方法的可靠性。

表2对几种常用位置预测模型进行了准确性比较，可以看出一阶二阶马尔可夫模型在出租汽车位置预测方面准确率并不理想；相对于普通隐马尔可夫模型，加入滑动窗口的改进模型对行程坐标的预测没有明显提升，但在目的地坐标预测与行驶里程预测方面准确率均有提升。这是因为滑动窗口模型的加入使模型能对当前位置附近的目的地进行选择，更契合出租车的行驶特点。

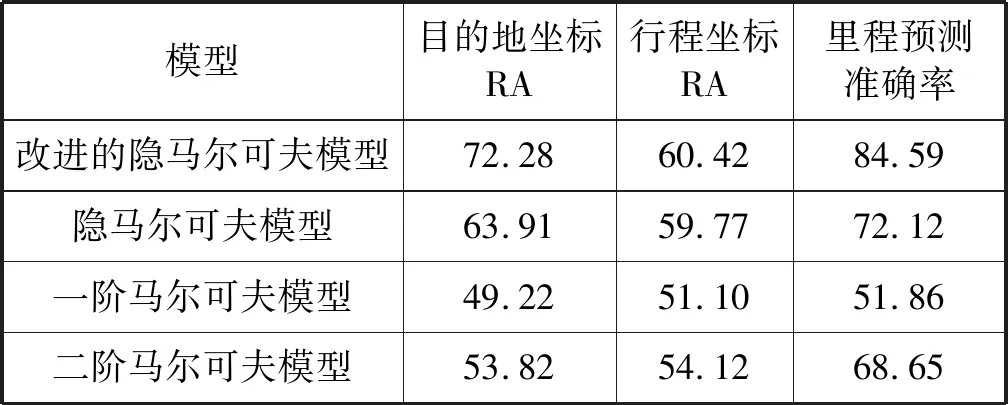
表2 预测结果对比 %

4 结 语

面向GPS轨迹数据，首先，通过载客状态与停留检测算法对轨迹进行状态分析；其次，为了契合出租汽车行驶的特点，将行程路径与目的地作为隐状态建立HMM；然后，使用滑动窗口模型对HMM的状态转移概率进行求解，使用Baum-Welch算法对观察概率与初始状态概率进行求解。实验表明，滑动窗口模型能很好地契合出租汽车行驶路径选择特点，本文建立的HMM在非市中心地区与出租汽车空载时有较高的准确率。该方法对出租汽车行程的目的地及行驶里程的预测准确度高，能较好应用于充电负荷预测。

由于本文未考虑同一目的地相似路径的选择问题，导致在路网情况相对更复杂的市中心区域行程预测误差较大。未来将会把几个可能影响相似路径选择的问题列入考虑：不同的驾驶员存在不同的路线选择习惯与路线长度衡量标准，这些特征应该会影响路径选择；交通的拥挤、道路的修缮等情况会对出租汽车的路径选择产生影响。未来工作将针对这些特征建立更复杂的模型用于预测。