地下空洞的面波场地效应数值模拟研究

2021-05-13刘争平刘茂洋

地震工程学报 2021年2期

黄果, 刘争平, 刘茂洋

(1. 西南交通大学, 四川成都 610031; 2. 中铁长江交通设计集团有限公司, 重庆 401121)

0 引言

随着城市基础设施建设和轨道交通的大力发展,大量地铁、隧道的修建以及其他地下空间的开发利用,形成了越来越多的人工地下空洞。地下空洞的存在破坏了原有岩层的整体性,导致地震波不只在横向均匀空间内传播,从而产生了场地效应,即地震波在传播过程中遇到不同岩层、断裂带、空洞等横向地质地貌会对地震动特性产生影响的现象。前人的研究表明,这些地下空洞产生的场地效应会对附近其他工程结构产生一定影响,存在潜在的工程隐患。

Pao[1]用波函数展开法研究了地下洞室的应力集中问题,发现地下空洞的存在会对地震波产生散射,从而改变波的动力学性质,在洞室周围形成应力集中,会对附近的工程结构产生震动放大等影响。梁建文等[2-3]运用级数解答和数值模拟,通过改变衬砌刚度、入射角度等分析了P波和S波入射时经过隧道引起的地表位移变化。梁建文等[4]利用波函数展开法,求得了半空间中空洞对瑞利面波散射的级数解和高频解答。Ren等[5]应用有限元数值模拟方法,通过改变隧道埋深和衬砌刚度分析了面波入射下隧道引起的近地表的位移变化。刘中宪等[6]采用间接边界积分方程法对地下隧道中瑞利面波的散射进行求解,探究改变隧道衬砌刚度、埋深等对面波散射的影响。Alielahi等[7]用面波入射平行的双洞隧道,收集近地表的数据并与无隧道时的数据对比发现:地下空洞的存在会使地震波能量分布发生很大变化。周凤玺等[8]运用波函数展开法得到弹性半空间中隧道对SH波散射的解析解,通过改变隧道半径、衬砌刚度和隧道埋深研究发现:隧道近地表位移随衬砌刚度和隧道埋深的减小而增加,随隧道半径的减小而减小。Narayan等[9]用有限差分法模拟了各种隧道模型的地震响应,也得到相似的结论。目前国内外学者主要是用体波研究地下空洞对地表震动的场地效应,或研究地下空洞的近地表场地效应,而对面波入射洞室周围的场地效应的研究较少。然而远场区的地震波能量主要是面波能量,空洞的场地效应不仅限于地表,所以系统地研究地下空洞面波的空间场地效应对建设施工、公路铁路选址选线都具有很重要的意义。

基于此,本文主要使用数值模拟方法分析地下空洞对面波传播的波场影响,研究地下空洞的空间场地效应,综合分析地下空洞的埋深和半径变化对空间场地效应的影响,并与已有物理实验结果进行对比检验,以验证本文数值模拟方法的可行性和所得数据的可信性。

1 方法原理

1.1 数值模拟方法

Abaqus 是当今常用的有限元软件之一,拥有丰富的材料库和单元库,具有强大的计算模拟能力,适用于处理高度非线性问题。完整的Abaqus计算分为前处理(网格划分)、模拟计算、后处理三个过程,本文用Abaqus显式算法的中心差分法进行计算。中心差分法不需要迭代求解,其本质是以差分代替微分,并对位移和加速度采用线性外插,因此为保证计算结果的精确性,步长取值不能过大。

数值模型的网格划分是把模型分为大量的离散单元,单元尺寸的不同会让计算结果产生相应的误差。一般来说单元尺寸越大计算结果越不精确,单元尺寸越小计算结果越符合真实情况,但是单元尺寸过小会带来巨大的计算压力。宗福开[10]的研究表明,在单元尺寸小于最小波长的1/π时,数值模拟可达合理的计算精度。本文选用四边形平面应力单元,单元尺寸为最小波长的1/20;采用20 Hz主频的雷克子波作为震源,其表达式为:

u(t) =[1-2(πf0)2(t-t0)2]·

exp[-(πf0)2(t-t0)2]

(1)

式中:t为雷克子波传播时间;f0为雷克子波主频;t0为雷克子波的主频时刻。

1.2 数值模型

1.2.1 模型尺度

瑞利面波是地震波的一种,是由体波传播到地表面时和地表面相互作用产生的。面波只存在于地表面附近,其能量随深度增加逐渐衰减。

面波主要能量集中在地表以下1个波长的范围内。由于波长为波速和频率的比值,因此面波的波长由地层的波速(或弹性参数)和传播面波的频率两个因数确定。例如,对于同一频率的地震波,场地越软弱,波速越低,波长就越短,即面波的穿透深度就越小;而对同一弹性参数场地,地震主频越低,地震波波长就越长,即面波的穿透深度就越大[11-12]。因此,为使研究结果对于实际变化的场地参数和地震的主频波长具有普遍意义,本文中的数值模型尺度均采用主波长归一表示,数值模拟结果均采用主波长归一显示,如图2、图3中横、纵坐标分别用主波长的倍数表示地层深度和测点到空洞中心的距离。

1.2.2 模型

图1为存在空洞场地的二维数值模型。定义波传播方向为x正方向,垂直于x方向向下为y正方向,即震源震动方向;定义位移在x方向上的分量为位移水平分量,在y方向上的分量为位移垂直分量。由表1所列材料参数和震源主频求得面波主波长λ=50 m,将空洞中心水平位置设在x=20λ处。因为面波能量主要集中在1个波长内,所以分别设计h=0.2λ、0.5λ、0.7λ、λ四个不同埋深的模型,对每一个埋深模型,设计了d=0.5λ、1λ、2λ三个不同直径进行研究。空洞场地效应的分析区域设置为:距离震源x=12λ～28λ,y=0～5λ。观测采样时长为2 s,采样间隔为0.000 2 s。

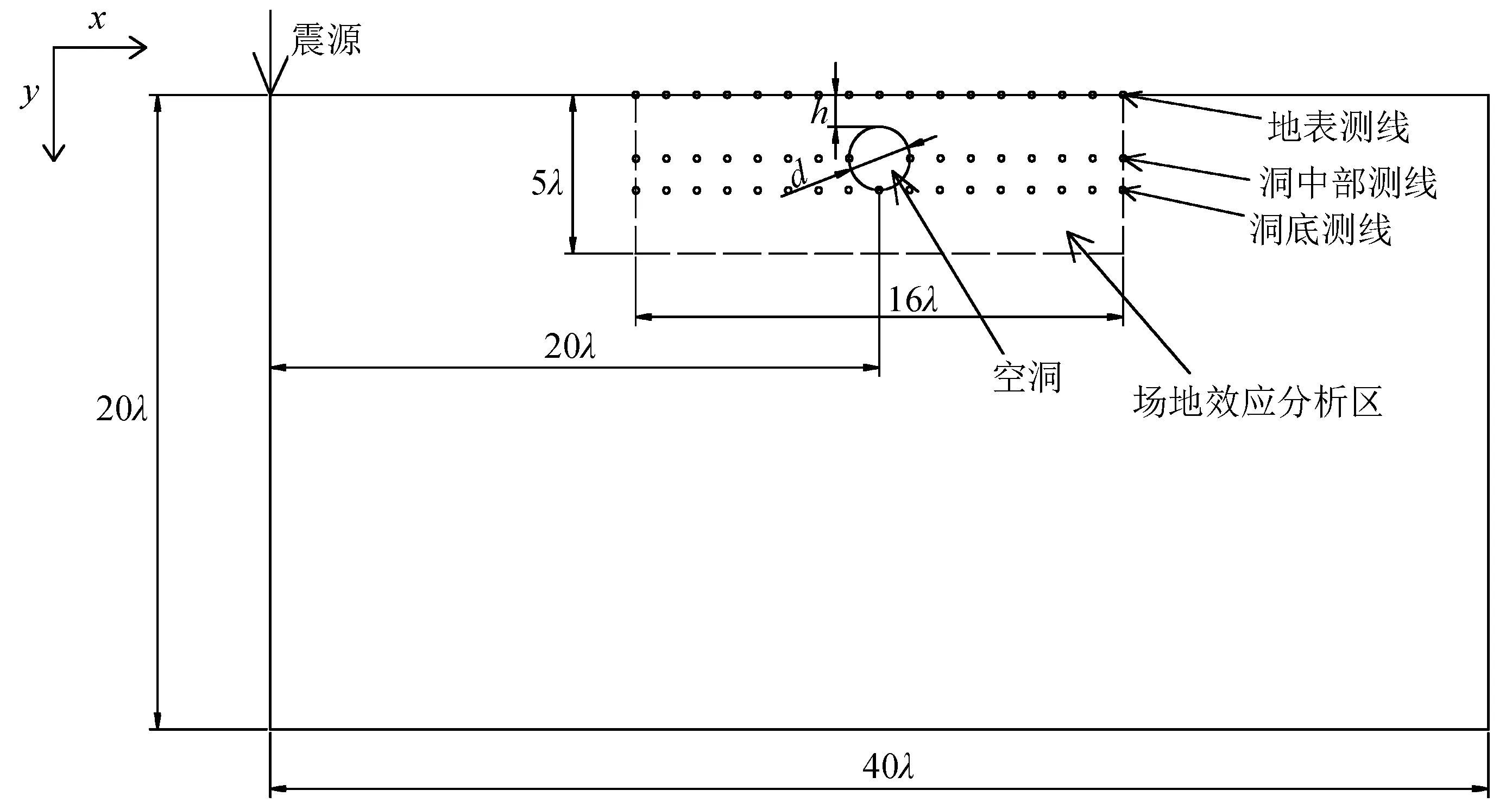
图1 空洞场地效应分析数值模型Fig.1 Numerical model for analysis of cavity site effect

表1 模型材料参数

根据文献[13]研究,距离震源3个波长外即可认为是远场区,远场区面波能量远大于体波能量,为地震波能量的主要部分。本文所有数值模拟研究均在远场区进行。

2 面波场地效应分析

2.1 空洞地层中面波传播的波场特征

本节主要通过数值模拟的波场快照和地震动记录对空洞地层中面波的波场特征进行研究。

图2(a)、(b)分别显示了空洞顶埋深h=0.2λ、直径d=1λ时模型的面波水平分量和垂直分量的波场快照。从图中可以发现,当面波传播到地下空洞位置会发生散射,因此会对面波能量的传播产生影响。其主要表现为:面波(R)传播到空洞时,部分能量转换为反射面波沿地表向反方向传播(RR),另一部分能量转换为新的面波沿洞壁传播(NR)。NR波部分能量转换为体波,主要为S波向空间扩散(RS),且这部分能量中大部分往空洞远源侧的右下区域空间传播,小部分通过洞壁反射回近源侧。面波通过空洞后形成一系列波串,即出现频散,波场中波的形态相较于到达空洞之前更为复杂。波场快照也显示,空洞远源侧右下区域传播的转换RS波具有很强的能量和很大的传播区域。

图2 空洞埋深h=0.2λ、直径d=1λ时面波的数值模拟波场快照图Fig.2 Snapshot of wave field in numerical simulation of surface wave with h=0.2λ and d=1λ

2.2 空洞场地效应特征

定义场地效应系数α为同一测点有空洞时波场最大位移与无空洞时最大位移的比值。α>1时空洞对位移产生放大效应,随α的增大放大效应越明显;α<1时空洞对位移产生减弱效应,随α的减小减弱效应越明显。显然场地效应系数α可以有效反映空洞存在时空洞周围岩土及地表的地震波能量或位移的变化情况。

图3(a)、(b)分别表示空洞埋深h=0.2λ、直径d=1λ时位移水平分量和垂直分量α值的空间分布情况。从图中可以看出,水平分量α的最大值出现在洞顶局部点处,达11.59。由于空洞的散射,空洞远源侧地下能量大幅增加,使得α值增大到5～7,空洞近源侧岩土体振幅出现小幅度加强,α值为2～3。在远源侧地表及近地表处出现小部分减弱区,α值为0.5～0.9。垂直分量的洞顶处α值较小,为0.5～0.9,而远源侧增强区位置与水平分量大致相同,α的最大值为6.52。由影响区域来看,空洞远源侧右下区域为空洞场地效应增大的主要区域,其位移水平分量和垂直分量的α值一般在3以上,最大可达7,即与无空洞时的震动幅值相比增大了3～7倍,且该增大区域分布范围很大,在深度上可达4λ,横向上可达6～7λ。由图2可知,这主要是由空洞对面波的散射所产生的向空洞远源侧右下区域传播的转换RS波能量所导致。图3结果还表明地下存在空洞时,位移水平分量的增强比垂直分量大。

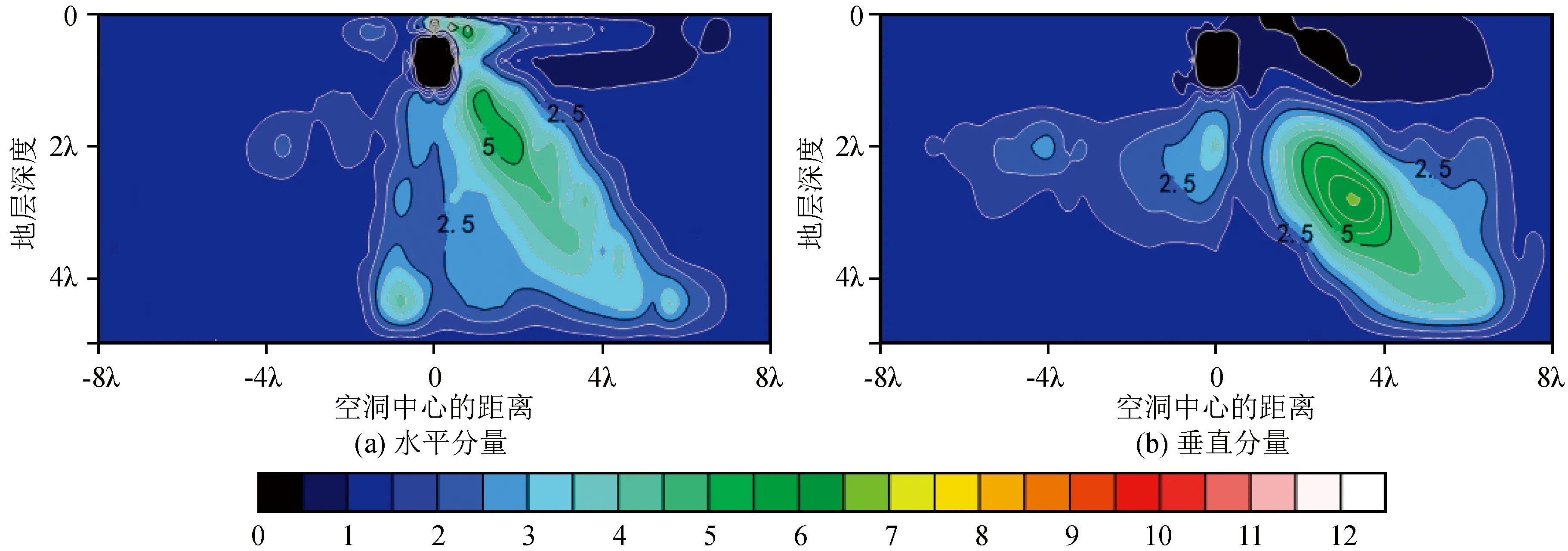
图3 埋深h=0.2λ、直径d=1λ时场地效应系数α值空间分布图Fig.3 Spatial distribution diagram of the value of site effect coefficient α with h=0.2λ and d=1λ

2.3 空洞埋深变化的场地效应

为研究空洞埋深对场地效应的影响,将数值模型的空洞直径固定为d=1λ,改变空洞顶埋深,以每个模型的地表、洞中部、洞底3条水平测线(测线位置见图1)的观测值分析研究场地效应系数α的变化情况。图4、图5和图6分别显示了洞径d=1λ不变、埋深h=0.2～1λ时,地表、洞中部、洞底的场地效应系数α的变化情况。图中纵坐标为空洞埋深与主波长的比值，横坐标为测点到洞中心的水平距离。

图4 空洞埋深变化时地表测线α值的分布图Fig.4 Distribution of α value of the surface survey line with different buried depth of cavity

图5 空洞埋深变化时洞中部测线α值的分布图Fig.5 Distribution diagram of α value of the survey line in the middle of cavity with different buried depth of cavity

从图4中可以发现空洞远源侧地表处约6～7个波长范围内,场地效应系数α<1,即能量有一定的减弱。随着空洞埋深增大到1个波长,场地效应系数α逐渐趋于1。图中也可看出,空洞埋深变化对水平分量的影响比垂直分量大。图5显示,在空洞中部左右约2个波长范围内,水平分量和垂直分量的场地效应系数α增大到2～4,但前者的场地效应系数α和影响区域均大于后者,且随着空洞埋深的增大其变化不大。图6显示,洞底处远源侧能量的增强更为明显,α增大到3～6,其分布范围为6～7个波长。同一埋深情况下水平分量的场地效应系数α最大值总是大于垂直分量。随着空洞埋深的增加,场地效应系数α的最大值减小,其影响范围也在减小。

图6 空洞埋深变化时洞底测线α值的分布图Fig.6 Distribution diagram of α value of the survey line at the bottom of cavity with different buried depth of cavity

2.4 空洞直径变化的场地效应

为研究空洞直径变化的场地效应,将数值模型的空洞顶埋深固定为h=0.2λ,改变空洞直径,以每个模型的地表、洞中部、洞底3条水平测线的观测值分析研究场地效应系数α的变化情况。图7、8、9分别表示洞顶埋深h=0.2λ、直径d=0.5～2λ时,地表、洞中部、洞底的场地效应系数α的变化情况。图中纵坐标为空洞直径与主波长的比值，横坐标为测点到洞中心的水平距离。

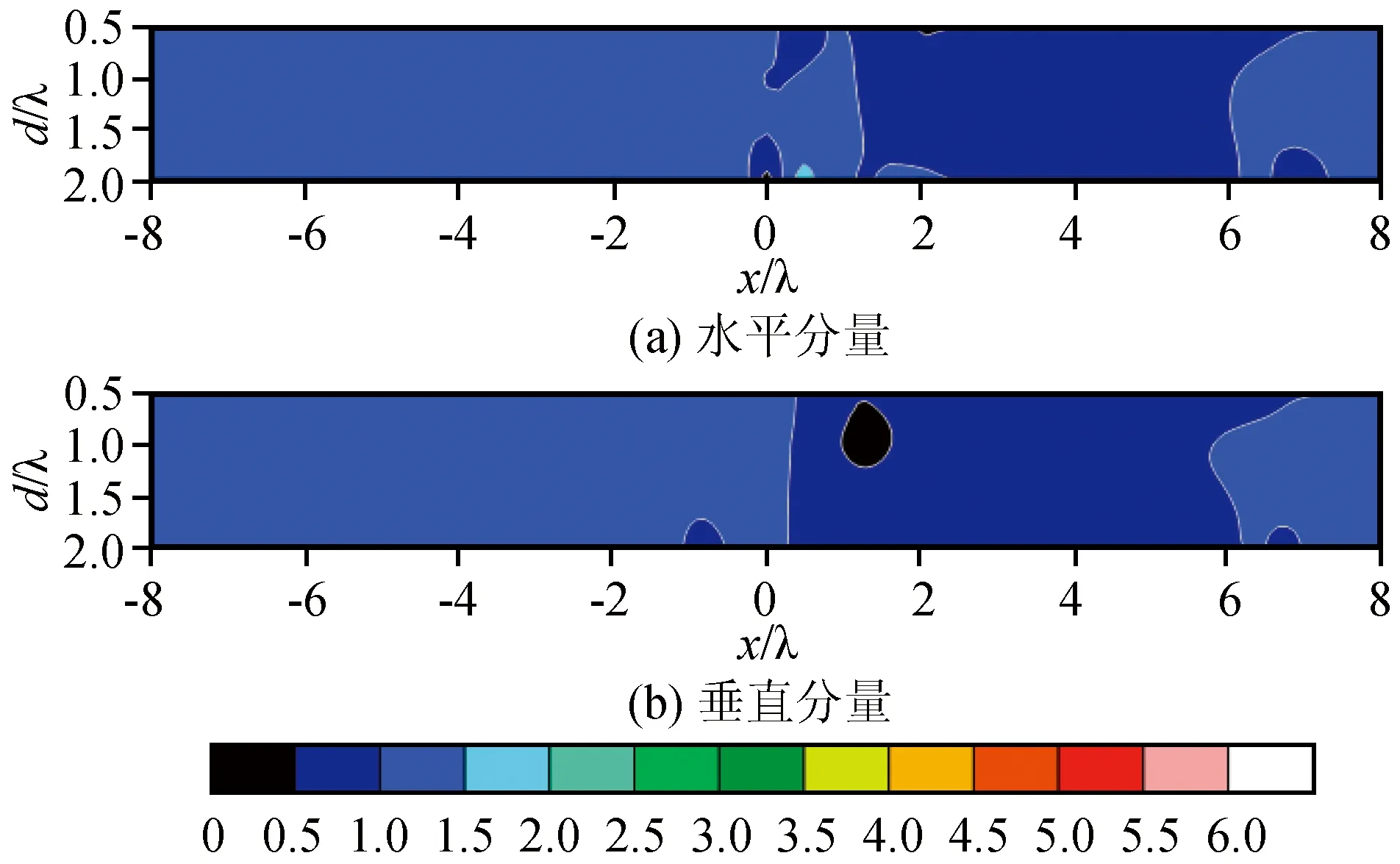
图7 空洞直径变化地表测线α值的分布图Fig.7 Distribution diagram of α value of the surface survey line with different cavity diameter

图8 空洞直径变化时洞中部测线α值的分布图Fig.8 Distributiondiagram of α value of the survey line in the middle of cavity with different cavity diameter

图9 空洞直径变化时洞底测线α值的分布图Fig.9 Distribution diagram of α value at the bottom of cavity with different cavity diameter

从图中可以发现,随着空洞直径的增大,空洞的场地放大效应迅速增大。与图4、5、6相似,在地表、空洞中部和底部,空洞直径变化对水平分量和垂直分量场地效应系数α的影响主要出现在空洞远源侧,分布范围可达6～7个波长,主要影响范围为洞周2个波长范围内。地表的场地效应系数α<1,空洞中部和底部的α值为3～6,出现场地放大效应,且水平分量的场地效应系数α的幅值和影响范围远大于垂直分量。

2.5 综合场地效应分析

图10(a)、(b)分别表示埋深和洞径变化时,水平分量和垂直分量的场地效应系数α最大值的变化情况。从图中可以看出,水平分量和垂直分量场地效应系数α的最大值均随洞埋深的增加而减小,随洞径增加而增加。图中还显示,垂直分量场地效应系数α最大值为6～7,而水平分量的α可高达12,水平分量具有更强的场地放大效应。此外当空洞埋深h<0.4λ时,水平分量的最大放大系数均高于7,对洞径变化不敏感。

图10 空洞直径和埋深都变化时α最大值的分布图Fig.10 Distribution diagram of the maximum α with different cavity diameter and buried depth

大多数地震的主频在10 Hz左右(如1971年阿根廷圣费尔南多地震主频10 Hz、1999年台湾南投地震主频11.6 Hz),对横波速度vS=1 000 m/s(面波速度vR≈0.92vS)的地层来说,其波长约为100～200 m,因此在地下空洞附近2个波长范围内(即200～400 m)修建地下结构物时应考虑场地效应带来的影响。

3 物理实验检验

为进一步验证以上数值模拟结果的准确性,将数值模拟得到的波场快照与已有实验得到的波场快照进行对照研究。

图11、12为文献[14]中用带空洞的有机玻璃进行超声物理实验所得到的波场快照,图中横、纵坐标分别表示到玻璃板左上角的横纵距离。图中可以看出:瑞利面波经过空洞后,位移的垂直分量和水平分量均会在空洞处散射转换为S波(本文中的RS),并向空洞远源侧右下方传播,因此空洞远源侧远地表处会出现震动增强区域。这与图2中数值模拟波场快照得到的结论是一致的,从而验证了本文数值模拟结果的可信性。