Electron acoustic solitary waves in unmagnetized nonthermal plasmas
2021-05-13MuhammadKhalidAqilKhanMohsinKhanDaudKhanSherazAhmadandAtaurRahman
Muhammad Khalid,Aqil Khan,Mohsin Khan,Daud Khan,Sheraz Ahmad and Ata-ur-Rahman
1 Department of Physics,Government Post Graduate College Mardan,Mardan 23200,Pakistan
2 Theoretical Plasma Physics Group,Department of Physics,Islamia College Peshawar (Public Sector University),Peshawar 25120,Pakistan
3 Department of Physics,Government Post Graduate College Nowshera,Nowshera 24100,Pakistan
Abstract Electron acoustic (EA) solitary waves (SWs) are studied in an unmagnetized plasma consisting of hot electrons(following Cairns-Tsalli distribution),inertial cold electrons,and stationary ions.By employing a reductive perturbation technique (RPT),the nonlinear Korteweg-de Vries(KdV) equation is derived and its SW solution is analyzed.Here,the effects of plasma parameters such as the nonextensivity parameter(q),the nonthermality of electrons(α),and the cold-to-hot electron density ratio (β) are investigated.
Keywords: Electron acoustic solitons,KdV equation,Cairns-Tsalli distribution
1.Introduction
In plasmas,electron acoustic waves (EAWs) contains hot inertialess electrons and cold inertial electrons.When inertial cold electrons oscillate,EAWs are produced,in contrast to inertialess hot electrons.Watanbe and Taniuti showed that if electrons in plasma have two different temperatures,i.e high and low,then an electron acoustic mode occurs.When the number density of hot electrons is smaller than that of those at lower temperatures,the electron acoustic mode is damped(landau),while in the opposite case,solitary waves(SWs)can be propagated [1].Yu and Shukla studied low-temperature cold-electron density and concluded that it strongly depended on frequency [2].They also discussed the solitons that are associated with modified EAWs.The topological behaviour of higher order modes (HOMs) in two-electron-temperature plasmas and the conditions under which HOMs can become weakly damped were qualitatively studied by Mace and Hellberg [3].The existence of modulational instabilities and also the occurrence of envelope solitary structures involving EAWs that propagate in unmagnetized plasma,which consist of cold electrons,hot electrons,and ions,meant that three components of plasma were discussed in [4].There are numerous differential equations that are used to describe many linear and nonlinear natural phenomena in different media such as shallow water,nonlinear optics,and plasma [5-12].
The study of nonlinear periodic waves has gained considerable interest within plasma physics; some examples are mentioned in[4,13-21].The properties of EAWs that propagate obliquely in magnetized plasmas composed of a cold magnetized electron fluid and a hot vortex-like distribution of electrons and ions were discussed by Mamun and Shukla,they studied the effects of the external magnetic field and obliqueness and found that they changed important properties of EAWs,such as amplitude and width [21].The electrostatic modes in an unmagnetized and homogenous plasma of three Maxwellian components: ions,hot electrons and cold electronswere studied by Gary and Tokar[22].Baluku et al[23]investigated EAWs in a plasma whose electron-velocity distribution was a combination of two kappa κ distributions with different densities,temperatures and values of kappa κ,using kinetic theoretical approach.They concluded that when the hot and cold densities became equal,then the damping of EAWs in this region was very small.Lu et al performed a 1D particle in cell electrostatic stimulation to analyze the nonlinear evolution of electrostatic waves excited in an unmagnetized plasma which was composed of cold,hot and beam electrons [24].Shukla et al [25] performed a theoretical investigation which helped to confirm the properties of multidimensional(3D)electron acoustic solitary waves(EASWs)in a magnetized plasma composed of stationary ions and magnetized cold electrons with an amount of beam electrons and magnetized hot electrons which obeyed a vortex-like distribution.They derived and mathematically solved a modified 3D KdV equation and concluded that 3D EASWs evolve with time.Younsi and Tribeche [26] showed the occurrence of arbitrary amplitude EA solitary potentials in a plasma composed of ions,cold electrons (inertial) and hot superthermal electrons.They concluded that localized EASWs can exist in such plasmas.They also found out that when the superthermal character of plasma increases,the potential pulse amplitude also increases,but its width becomes narrower.Moreover,the superthermal effect makes the EA solitary structures more spiky.In this paper,we describe a search for the propagation of EAWs in a plasma consisting of Cairns-Tsalli distributed hot electrons,inertial cold electrons and stationary ions.
This paper is organized as follows: model equations are given in section 2; the linear dispersion relation is derived in section 3;the derivation of the KdV equation by RPT and its SW solution are presented,respectively,in sections 4 and 5;a discussion is offered in section 6.In section 7,the conclusions of our work are presented.
2.Basic equations
We consider a three-component plasma comprising cold electrons,hot electrons and stationary ions.The hot electrons follow a nonthermal distribution,inertial cold electrons and the ions are stationary in the background.The dynamics of the cold electrons are governed by the following set of normalized equations:
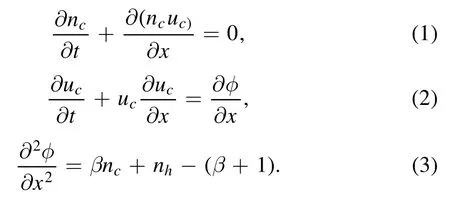
The hot electrons are assumed to follow Cairns-Tsalli distribution [27,28],given by:
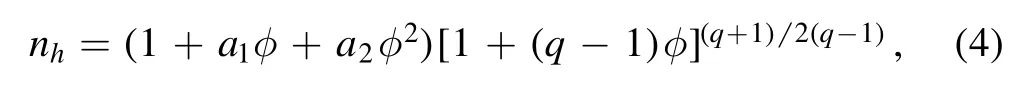
where we define

and
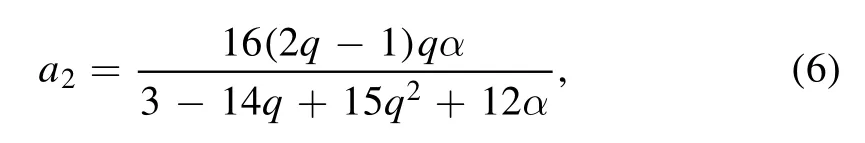
where q is a real parameter,known as nonextensivity [29],and α is a real parameter associated with the number of nonthermal electrons in the distribution [30].Here,nc(nh) is the cold (hot) electron number density scaled by its equilibrium value nc0(nh0),ucis the cold electron fluid velocity scaled by the EA speedandis the normalized electrostatic wave potential.The space variable (x)and time variable (t) are scaled byandrespectively.The cold-to-hot electron density ratio,The subscript ‘c’ is dropped from the rest of calculation for simplicity.
For φ ≪ 1,equation(4)can be expanded in the power of the potential as,
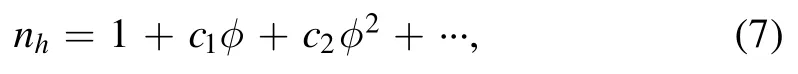
where c1and c2are defined,respectively,asc1=andUsing equation (7) in equation (3),we obtain

3.Linear analysis
Following the method provided in [27],we linearize equations (1)-(3) using a standard procedure where the firstorder quantities are proportional to exp (ikx- iωt),thus we obtain a linear dispersion relation in the form of

where c1is defined above.
4.Derivation of the KdV equation
To derive the KdV equation,we should adopt the RPT.The stretching of coordinates is given as

where vphis the EA speed and is interpreted as the phase velocity,and ∈is a very small real parameter.
Expanding the dependant variables as follows,
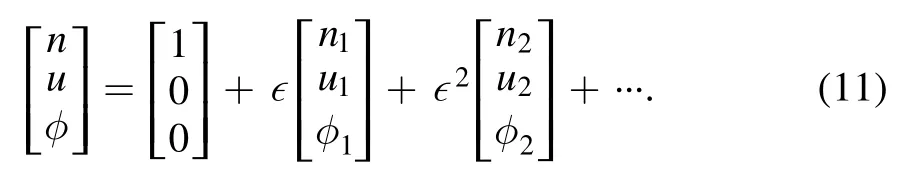
Using (10) and (11) in equations (1),(2),and (8) gives the first order quantities as

and

Comparing equations (12) and (14),we get

Moving to the next order of ∈i.e.the second order perturbation,we get
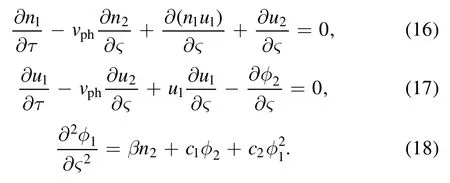
Now solving equations (16)-(18) and making the use of first order quantities,we get
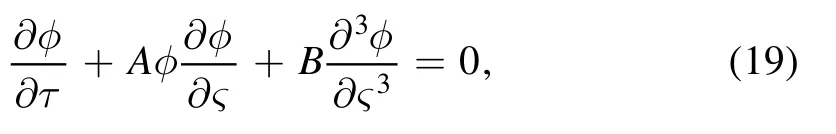
where φ1≡ φ.This is the KdV equation for EA waves,where the nonlinear coefficient A and the dispersion coefficient B are given below:
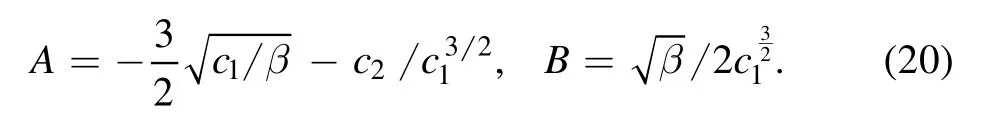
5.The SW solution
To solve equation (19),we define a traveling-wave transformation η = ς - v0τ,in respect of which the wave is stationary,where v0is the velocity of the EASW.Using this transformation,equation (19) takes the following form
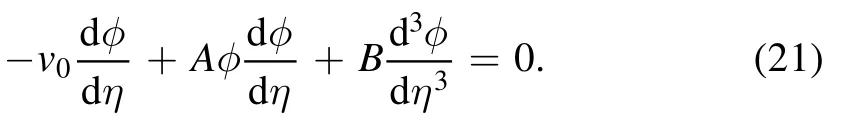
By solving the above equation using integration and some mathematical steps,we get

6.Numerical analysis
To study the behaviour of EASWs,we have derived the KdV equation,which we use to study the effects of various parameters involved in the coefficients of the KdV equation.These effects are studied with the help of various graphs that are discussed below.
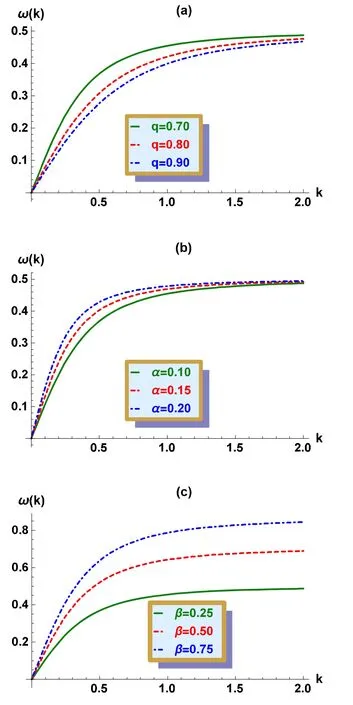
Figure 1.Plots of ω(k) versus k,for different values of: (a)nonextensivity parameter q;(b)nonthermality parameter α;(c)coldto-hot electron density ratio parameter β.
If we take into account the dispersion relation equation (9),the value of ω is strongly dependent upon the value of k.As shown in figure 1,ω increases as the value of k increases.A discussion of the ω-k graph depends upon c1,which is a further function of α,q and β.Figure 1(a) shows that whenever the value of q increases,a decrease occurs in the ω-k graph.This means that ω is inversely proportional to the parameter q.On the other hand,figure 1(b) shows the effect of α parameter on the ω-k graph.When the value of α increases,the graph also increases,as shown in the figure.Therefore,it shows a direct relation.Figure 1(c) shows the effect of β.As it is clear from equation (9),ω increases with an increase in the value of β,that is why the effect of β on the ω-k graph shows a direct variation,i.e.whenever β increases,the graph also changes to a higher value on the ω axis,as shown in figure.
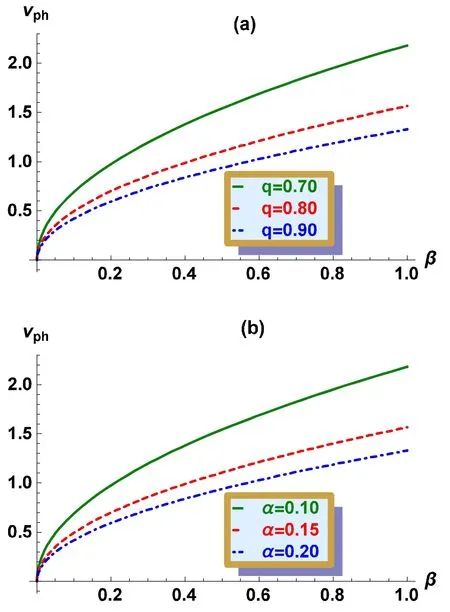
Figure 2.Variation of vph versus β for different values of: (a) the nonextensivity parameter q; (b) the nonthermality parameter α.
We now discuss the phase velocity of EASWs as given by equation(15).From the equation,it is clear that the phase velocity is directly proportional to β and inversely proportional to c1,which leads our discussion to study the effects of the parameters α,q and β on vph.Figure 2 presents the vph-β graph,which shows that the phase velocity increases as the value of β increases.Figure 2(a) shows that the q parameter has an inverse response to the vph- β graph,similarly α also affects the phase velocity: if α increases then the graph decreases.The effects of α and q parameters on the vph-β graph are shown in figures 2(a) and (b).
Moving to a study of the EASW,the nonlinear coefficient,A,and the dispersion coefficient,B,present in the KdV equation (19) are functions of various relevant plasma parameters.These parameters affect the structural characteristics of the pulses and may therefore lead to the generation of various kinds of EA solitary structures in a given plasma system.Figure 3 shows the SW solution for φ(η) versus η.Only negative pulses have been observed for the given plasma parameters α, q,and β.Figure 3(a)shows the effect of the q parameter on EASWs; if the value of q increases,both amplitude and width of the soliton decreases.The dependency of the SWs on α parameter is shown in figure 3(b).If we increase the value of α then the amplitude of the soliton decreases while its width increases,as shown in the figure.A similar situation occurs in case of β.An increase in β has the result that the amplitude of the soliton decreases,while its width increases,as shown in figure 3(c).
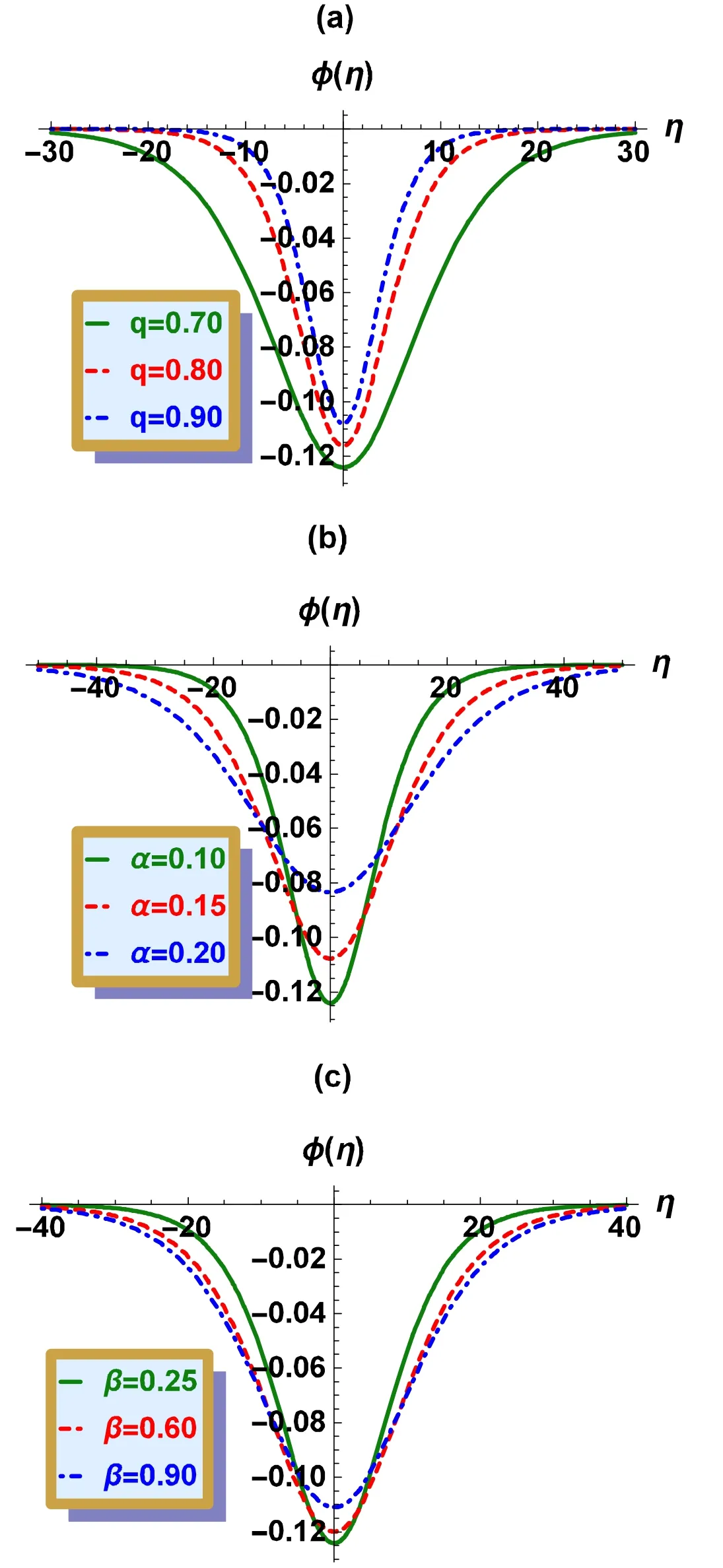
Figure 3.Variation ofφ (η) versus η for different values of: (a) the nonextensivity parameter q; (b) the nonthermality parameter α; (c)the cold-to-hot electron density ratio parameter β,with v0 = 0.1.
7.Conclusions
The propagation of EASWs was studied in an unmagnetized plasma consisting of hot electrons (following Cairns-Tsalli distribution),inertial cold electrons,and stationary ions.By employing RPT,the nonlinear KdV equation was derived and its SW solution was analyzed.The effects of plasma parameters such as the nonextensivity parameter (q),the nonthermality of electrons (α),and the cold-to-hot electron density ratio (β) were investigated.
Due to the variation of α, q and β,the KdV equation only gave the negative potential EA solitary structures for a given plasma system.It was found that smaller(in amplitude)and wider (in width) wave structures were obtained with increasing values of α and β.Also,smaller and narrower solitary structures were obtained with increasing values of q.
This work may be helpful in various space observation and astrophysical environments,where nonthermal nonextensive electrons are present [31,32].
杂志排行
Communications in Theoretical Physics的其它文章
- Insight into the chemomechanical coupling mechanism of kinesin molecular motors
- A pedagogical review on solvable irrelevant deformations of 2D quantum field theory
- Ab initio study of the effects of helium on the mechanical properties of different erbium hydrides
- Interface water-induced hydrophobic carbon chain unfolding in water
- A simplified Parisi ansatz
- Vector kink-dark complex solitons in a threecomponent Bose-Einstein condensate
