Effect of entanglement embedded in environment on quantum non-Markovianity based on collision model

Xiao-Ming Li (李晓明),Yong-Xu Chen (陈勇旭),Yun-Jie Xia (夏云杰)and Zhong-Xiao Man (满忠晓)

School of Physics and Physical Engineering,Shandong Provincial Key Laboratory of Laser Polarization and Information Technology,Qufu Normal University,Qufu,273165,China

Abstract By means of collision models (CMs) where the environment is simulated by a collection of ancillas consisting of two entangled qubits,we investigate the effects of entanglement in the environment on the non-Markovianity of an open quantum system.Two CMs are considered in this study,in the first one the open quantum system S directly collides with the environment,while in the second one the system interacts with two intermediate qubits which,in turn,are coupled to the environment.We show that it is possible to enhance the non-Markovianity by environment entanglement in both models.In particular,in the second model,we show that the initial state of the auxiliary qubits can also affect the non-Markovianity of the system and there exists the optimal combination of the initial environmental state and the initial state of auxiliary qubits.In this case,the non-Markovianity can be greatly enhanced.

Keywords: collision model,entanglement,non-Markovianity

1.Introduction

A quantum system inevitably interacts with its surroundings,resulting in a non-unitary evolution of the system.We can use the theory of an open quantum system [1] to deal with such dynamic processes.For Markovian dynamics[2,3],the system information can only flow from the system to the environment,that is,the environment is memoryless.By contrast,for non-Markovian dynamics,the system information that has flowed into the environment will partially or completely flow back from the environment to the system.In other words,the system can retrieve some information lost during the evolution of the system.In recent years,the study of non-Markovian dynamics has attracted extensive attentions and becomes a topical field[4-21],particularly in the characterization and measure of non-Markovianity[22-31].For example,the Breuer,Laine,and Piilo(BLP)measure [29] is proposed based on the trace distance which quantifies the degree of distinguishability between two arbitrary different initial states.Since the trace distance of any pair of states tends to contract in the Markovian process,the growth of the trace distance indicates the appearance of non-Markovian dynamics.

The collision model (CM),an efficient microscopic framework for simulating the open dynamics of a quantum system,was initially proposed by Rau in 1963 [32].In the memoryless CM,the environment is assumed to consist of a large number of uncorrelated particles prepared in the same states.The system interacts/collides with a fresh environmental particle each time.That is,the system qubit can collide with each environment qubit only once.Each collision can be described by a unitary operationTherefore,the dynamics of the open system is Markovian.To enable the CM to effectively simulate the non-Markovian dynamics of open quantum system,we can modify the memoryless CM by introducing the composite structure of the system [33] or the collision between environment qubits[34,35].More recently,various extended CMs have been used to investigate the non-Markovian dynamics of open quantum systems[33,36-48].Moreover,the CMs have been used widely in other fields,such as quantum optics [49,50] and quantum thermodynamics [2,51-55].

Figure 1.Sketch of collision model I.(a) The system qubit S collides with subancillas R11 and R12 in ancilla R1,respectively.(b) The two subancillas in ancilla R1 collide with the two subancillas in ancilla R2,respectively.The dotted blue lines in graph denote the correlation among S,R11 and R12 established after their collisions (i.e.after Step (a)).(c) The ancilla R1 is traced out and the processes (a) and (b) are repeated.

The non-Markovianity of the open quantum systems dynamics is closely associated with the system-environment correlations [39,46].The initial environmental states will inevitably affect the non-Markovianity of the open systems.Therefore,it is necessary to study the effect of the environmental state on the non-Markovianity in the open system dynamic process.In[44],the authors have investigated the smallest set of requirements for inducing non-Markovian dynamics in a CM of open quantum systems by introducing correlations in the state of the environment.It is noteworthy that the interaction between environmental particles was not considered in this study.The authors in [47] have studied the effect of entanglement on the non-Markovianity by considering two-mode squeezed vacuum state for the environment.It was found that under certain conditions,the entanglement can enhance the non-Markovianity of the system.In this work,we further study the effects of various environment states on the non-Markovianity.Therefore,we construct two types of CMs(hereafter denoted as CM I and CM II,respectively),in which the open system is a qubit and the environment consists of a large collection of identical ancillas.Each ancilla is bipartite,consisting of two subancillas.For CM I,the open system directly collides with the environment ancillas.For CM II,the system interacts with the environment through two auxiliary qubits.Based on these two types of CMs,we investigate the effect of the entanglement in the environment on the quantum non-Markovianity and the possibility of enhancing the non-Markovianity by taking the intracollision between reservoir ancillas into account.

2.Measure of non-Markovianity

Various methods for the measure of non-Markovianity have been proposed [22-31].In our work,we adopt the BLP measure proposed in [29],which can be expressed as

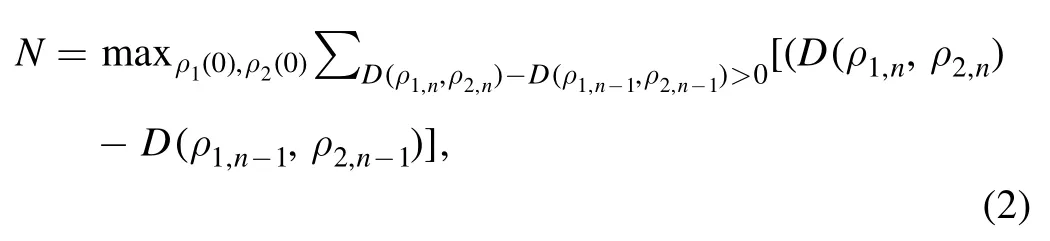
whereρm,nis the state of the system after n rounds of collisions from the initial stateρm(0)withm=1,2.

3.Non-Markovianity in CM I

Different from the standard CM,in our first model,as shown in figure 1,the environment is simulated by a large collection of identical ancillas{Rn},each of which is bipartite,consisting of two subancillasRn,1andRn,2,and each subancilla is modeled as a qubit.The system qubit,and reservoir subancillas are described by Hamiltonians (we set ħ= 1 in this paper)andrespectively,where the labelsωand()ωRn,12are the corresponding transition frequencies of the system qubit and reservoir subancillas (for simplicity,we assumeωS=ωRn,1(2)=ωin this paper),= ∣ 1〉X〈 1 ∣ - ∣ 0 〉X〈0∣is the Pauli operator and{∣ 0 〉X,∣ 1〉X}(X=S,Rn,1(2))are the logical states of the qubitX.

The interaction between the system and environment can be illustration as shown in figure 1.In the beginning,the system S collides with the subancillasR1,1andR1,2in the first r eservoir ancillaR1,respectively.After the collisions,they are correlated,as shown by the dotted line in figure 1(b).Now,each subancilla inR1carries part of the system information.Subsequently,an intracollision occurs between reservoir ancillasR1andR2,which is accomplished by colliding each pair ofR1,kandR2,k(k= 1,2),respectively.As a result,the correlation among S,R1,1,R1,2,R2,1andR2,2is established and a round of collisions is completed.Then the subancillasR2,1andR2,2also carry part of the system information,which will partly flow back to the system S in the next collision round.Taking the partial trace of the total stateρSR11R12R21R22of S,R1,1,R1,2,R2,1andR2,2with respect to ancillaR1,we can obtain the reduced stateρS R21R22of S,R2,1andR2,2,which is the initial state of the next round of collisions,and so on in a similar fashion.Therefore,from the reduced stateρSRn+1,1Rn+1,2of S,Rn+1,1andRn+1,2obtained at the nth round of collisions,the total state of S,Rn+1,1,Rn+1,2Rn+2,1and Rn+2,2at the(n + 1)th round of collisions can be obtained as

whereρRn+2,1Rn+2,2is the state of subancillasRn+2,1andRn+2,2.By tracing out ancillaRn+1,the reduced stateρSRn+2,1Rn+2,2of S,Rn+2,1and Rn+2,2can be obtained.In this way,we establish an iterative relationship between the stateρSRn+2,1Rn+2,2at the(n + 1)th collision and the stateρSRn+1,1Rn+1,2at the nth collision.Then the reduced state of the system at the (n + 1)th collision round can be obtained by tracing out the environmental degree of freedom,and it is expressed as

For the collision between the two qubits,the dynamical map that governs the unitary time evolution can be expressed as

We assume that the two subancillas in each reservoir ancilla are initially in entangled state with the form

Figure 2(a) shows the dependence of non-Markovianity N onγRRfor different entangled environmental states.As shown,for a givenθ,there is a threshold of intracollision strengthγRR,above which the system exhibits non-Markovian dynamics.The thresholds of intracollision strengthγRRdepends on the entangled states of the environment.The dependence of the non-Markovianity N on the initial entangled states and the interaction strengthγRRis shown in figure 3,from which the thresholds ofγRRfor a given initial entangled state of the environmentθare depicted clearly.It is worth noting that in comparison with the separable environment state withθ= 0,some specific choices of entangled states result in the smaller thresholds ofγRR,which means that in these cases the entanglement in the environment can be used to trigger the non-Markovianity.However,one can see that the non-Markovianity is even easier to activate as concurrence drops such that the easiest case indeed corresponds to the separable environmental state∣ 11〉 (i.e.θ= 0.5π),as shown in the region between the two dashed red lines.Turning back to figure 2(a),in the non-Markovian regime,the non-Markovianity N increases monotonically with the intracollision strengthγRR.Compared with the case ofθ= 0,some special entangled environment states (e.g.θ= -π/4,as shown by the dashed red line) can enhance the non-Markovianity for a relatively largeγRR.To fully grasp the effect of the initial environmental state on the non-Markovianity,in figure 2(b),we show the dependence of the non-Markovianity on the entanglement in the environment for different intracollision strengths.Note that for the sake of comparison,we plot several lines parallel to the horizontal axis in the figure based on the corresponding values of N withθ= 0.One can observe that for some initially entangled environmental state,e.g.θ= -0.04π,-0.46π,compared with the case of the separable environment state withθ= 0,the non-Markovianity of the system can be enhanced only within a certain range of intracollision strength.While for some other initial entangled environment states,e.g.θ= -0.25π,only when the intracollision strengthγRRexceeds a certain value,the non-Markovianity of the system can be improved.To be clear,in addition to the enhancement of non-Markovianity,the entanglement embedded in the environment can also suppress the non-Markovianity.In particular,when the values of the interaction strengthγRRis relatively small (e.g.γRR= 1.15),the entanglement in the environment can cause the non-Markovianity to vanish within several finite intervals ofθ,as shown by the solid black line.In other words,by changing the initial entangled environment state,the successive transitions between non-Markovian and Markovian regimes for the system dynamics can be achieved.Therefore,based on the analysis above,one can choose the appropriate initial entangled environmental state according to the intracollision strength between the reservoir ancillas to enhance the non-Markovianity of the system.

Figure 2.(a) Non-Markovianity against the interaction strength γRR for the different entangled environmental state.(b) Non-Markovianity against the entangled environmental state for different interaction strengths γRR.The parameters are given by γSR = 0.1and ω = 1.

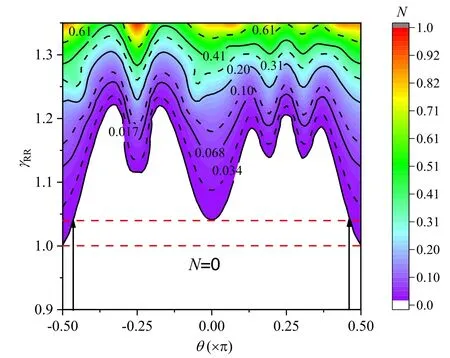
Figure 3.Non-Markovianity N versus the interaction strength γRR and the initial entangled environmental state.In this plot we used γSR = 0.1and ω = 1.

Furthermore,as shown in figure 2(b),for a given intracollision strengthγRR,the effect of the entanglement in the environment on the non-Markovianity depends completely on the entangled environment state(i.e.the value ofθ)and is not directly related to concurrenceCRof the environment state∣ Φ(θ) 〉.In other words,different entangled environmental states with the same values ofCRmay impose different effects on the non-Markovianity of the system.For example,for the initial environmental states∣ Φ(0 .25π)〉and∣ Φ (- 0.25π)〉,when the value ofγRRis relatively large,the effect of the entanglement on the non-Markovianity is diametrically opposite.

4.Non-Markovianity in the CM II

In the second CM (a composite CM [33]),the composite system is tripartite,as shown in figure 4,which consists of the system S of interest and two auxiliary qubits S1and S2.The auxiliary qubit is described by the HamiltonianThe system qubit S indirectly interacts with the reservoir ancillas through collisions with the two auxiliary qubits S1and S2.Under certain conditions,the model can simulate a quantum emitter in dissipative contact with a reservoir featuring a spectral density that is the sum of two Lorentzian distributions [33].

For the composite CM,the interaction mechanism between the system and the environment is shown in figure 4.Firstly,the system qubit S collides with auxiliary qubits S1and S2,respectively,hence,they are correlated.Next,S1and S2collide with the subancillasR1,1andR1,2in ancillaR1,respectively,and the correlation among S,S1,S2,R1,1andR1,2is established.Next,R1,1andR1,2collide with the two subancillasR2,1andR2,2in ancillaR2,respectively.As a result,the system qubit,auxiliary qubits and the reservoir ancillasR1andR2are correlated with the total stateρSS1S2R1,1R1,2R2,1R2,2and a round of collisions is completed.Tracing out the first reservoir ancillaR1,we obtain the reduced stateρSS1S2R2,1R2,2of S,S1,S2,R2,1andR2,2,which is the initial state of the next round of collision.As a consequence,based on the interaction mechanism of the model,the total state of S,S1,S2,Rn+1,1,Rn+1,2,Rn+2,1andRn+2,2at the (n+1)th round of collision is determined from the nth round of collision as

Figure 4.Sketch of collision model Ⅱ.(a) Pairwise collisions (S-S1,S-S2) occur between system qubit and auxiliary qubits,hence they are correlated.(b) Auxiliary qubits S1 and S2 collide with the subancillas R11 and R12 in ancilla R1,respectively.The dotted blue lines in the graph denote the correlation among S1,S2 and S established after their collisions (i.e.after Step (a)).(c) The two subancillas in ancilla R1 collide with the two subancillas in ancilla R2,respectively.The dotted blue lines denote the correlation among S,S1,S2,R11 and R12 established after Step (b).(d) The ancilla R1 is traced out,and then the processes (a)-(c) are repeated.

whereρSS1S2Rn+1,1Rn+1,2is the reduced state of S,S1,S2,Rn+1,1andRn+1,2at the nth collision,ρRn+2,1Rn+2,2is the initial state of subancillasRn+2,1andRn+2,2.The reduced state of the system at the(n + 1)th collision round can be obtained by tracing out the degrees of freedom of the environment and the auxiliary qubits,which is expressed as

Similarly,we assume that the two subancillas in each reservoir ancilla are initially in entangled state with the form of equation (9).For simplicity,we assume that there is no interaction between the auxiliary qubits S1and S2,and we setandin this section.

4.1.Separable auxiliary qubits state

In this section,we assume that the initial state of the auxiliary qubits S1and S2are in their ground states∣0〉 .We first study the non-Markovianity in the absence of intracollision between r eservoir ancillas,i.e.γRR= 0.The dependence of the non-Markovianity N on the interaction strengthγSRfor different initial entangled environmental states is shown in figure 5(a).We can see that the non-Markovianity decreases monotonically with the increase ofγSR.This indicates that the strong interaction between the system and the environment will weaken the non-Markovianity,consistent with the results presented in[48].Figure 5(b)shows the non-Markovianity N against the interaction strengthγSSfor different initial entangled environmental states.We notice that the non-Markovianity can be activated only when the interaction intensityγSSexceeds the threshold,which depends on the initial environment state.It should be emphasized,compared with the separable environment state withθ= 0,the entanglement embedded in the environment enlarges the threshold ofγSS(see the inset of figure 5(b)).In other words,the entanglement in the environment makes it harder to activate the non-Markovianity of the system.Once activated,the non-Markovianity N increases monotonically withγSS.Moreover,when the value of the collision strengthγSSis relatively small,the entanglement embedded in the reservoir can enhance the non-Markovianity for some particular values ofθ(e.g.θ=π/4,as shown by the dashed red lines in figures 5(a)and(b)).However,for the relatively large value ofγSS,the entanglement in the reservoir can only weaken the non-Markovianity.

Figure 5.(a) Non-Markovianity against the interaction strength γSR for different initial entangled environmental state with γSS = 0.01.(b) Non-Markovianity against the interaction strength γSS for different initial entangled environmental states with γSR = 0.1and ω = 1.

Next,we discuss the case in which the intracollision between reservoir ancillas is taken into account.In figure 6(a),we plot the non-Markovianity N as a function ofγRRfor different entangled environmental states.It is clear that the variations of non-Markovianity N with respect to the interaction strengthγRRare nonmonotonic,which shows the behavior of decreasing first and then increasing.For some initial entangled environment states,e.g.θ= ±π/4,the entanglement in the environment can enhance the non-Markovianity when the value ofγRRis relatively small.However,with the increase ofγRR,the entanglement in the environment can cause the non-Markovianity of the system to vanish completely within a finite interval of intracollision strengthγRR,and then revive,as shown by the dashed blue line and dotted red line in figure 6(a).That is to say,successive transitions between non-Markovian and Markovian regimes for the system dynamics can be realized by manipulating the intracollision strengthγRRfor some particular initial entangled environment states.The interval of the intracollision strengthγRRin which the non-Markovianity N remains zero value becomes smaller with the increase of interaction strengthγSS,as shown in figure 6(b).However,it can be seen from figure 6(c) immediately (for the sake of comparison,we plot two horizontal dashed green lines in figure 6(c)) that only when the coupling strength between the system and the auxiliary qubits is small (e.g.γSS= 0.01,0.015),can the entanglement in the environment (θ= ±π/4) enhance the non-Markovianity of the system.

4.2.Entangled auxiliary qubits state

In this section,we assume that the two auxiliary qubits are initially in entangled statesinβ∣11〉S1S2withβ∈ [ -π/ 2 ,π/2] .It is noteworthy that for reasons similar to those mentioned in the previous section,we only discuss the case where the auxiliary qubits are in entangled state described by∣ Ψ(β) 〉.

Figure 7(a) shows the dependence of the non-Markovianity N on the intracollisions strengthγRRfor different initial states of the auxiliary qubits whenθ=π/ 4.When the auxiliary qubits are initially in certain entangled states,e.g.β= -π/4,compared withβ= 0 (as shown by the solid black line in figure 7(a)),the non-Markovianity of the system is improved significantly within a definite range ofγRR,as shown by the dotted blue line.This indicates that it is feasible to further enhance the non-Markovianity by selecting the appropriate initial entangled state of the auxiliary qubits.However,for some other initial auxiliary qubit states,compared withβ= 0 (as shown by the solid black line),the non-Markovianity of the system reduced,e.g.β= -π/3.Even in some cases,e.g.β=π/ 4,the non-Markovianity of the system is severely weakened.These findings indicate that the entanglement embedded in the environment and in the auxiliary qubits jointly affect the non-Markovianity of the system.However,the total effect of the two on the non-Markovianity is not a simple superposition of their respective effects on it,as shown in figure 7.For example,for bothθ=0,β=π/4 (as shown by the dashed red line in figure 7(b))andθ=π/ 4 ,β=0(as shown by the solid black line in figure 7(a)),the non-Markovianity of the system is enhanced.However,whenθ=π/ 4,β=π/ 4 (as shown by the dashed red line in figure 7(a)) the non-Markovianity is reduced.Consequently,there must be an optimal combination of∣ Φ(θ) 〉 and∣ Ψ(β) 〉 which can greatly enhance the non-Markovianity of the open quantum system.For the parameters considered,we determined the combination{∣ Φ (π/4) 〉 ,∣ Ψ (-π/4) 〉}via numeral simulations,as shown in figure 8.It has been demonstrated that the CM can be realized in artificial systems,such as the superconducting quantum circuits [60] and the optical scheme [35,61].These provide the potential candidates for the implementation of our scheme.Hence,our scheme is effective for improving the non-Markovianity and is expected to provide a certain reference for some quantum information tasks,which is conducive to the development of quantum information processing.

Figure 8.Non-Markovianity N versusθ and β.The parameters are given by γSS = 0.01,γSR = 0.1,γRR = 0.03and ω = 1.

5.Conclusions

In summary,we have investigated the effects of the entanglement embedded in an environment on the non-Markovianity of the open quantum system dynamics by means of CMs.In CM I,the system qubit directly collides with the environment ancillas.We show that for some initial entangled environment states,the entanglement embedded in the environment can enhance the non-Markovianity of the system when the intracollision strength is relatively larger.Furthermore,we find the effect of the entanglement embedded in the environment on the non-Markovianity is not directly related to the entanglement degree.In CM II,the system interacts with the environment through two auxiliary qubits.The results show that,similar to the former,some initial entangled environment states can enhance the non-Markovianity of the system in certain conditions.In particular,compared with the case of the separable auxiliary qubit state,we demonstrate that the appropriate initial entangled auxiliary qubit states can further enhance the non-Markovianity.More importantly,there exists an optimal combination of initial environmental state and initial auxiliary particle state,which can greatly enhance the non-Markovianity.Finally,it is worth mentioning that in both models,the successive transitions from non-Markovian to Markovian dynamics can be realized by manipulating the state of each ancilla in the environment.

The non-Markovianity of the open quantum system can be used as a resource to enhance quantum information processing[17,62].Improving the non-Markovianity of the open systems is of great significance to the development of quantum information processing and quantum computation.In this regard,our results can provide an alternative for enhancing the non-Markovianity of the open system and might be useful in certain quantum tasks.

Acknowledgments

This work is supported by National Natural Science Foundation(China)under Grant No.61675115 and No.11974209,Taishan Scholar Project of Shandong Province(China)under Grant No.tsqn201812059 and Shandong Provincial Natural Science Foundation (China) under Grant No.ZR2016JL005.