考虑与过街行人冲突的道路右转机动车延误研究
2021-05-13李硕夏文慧李洁贺文
李硕, 夏文慧, 李洁, 贺文
(湖南大学 土木工程学院, 湖南 长沙 410082)
1 引言
随着中国城市化发展的不断提速,交通冲突现象日益严重。而步行在如今政府大力倡导的绿色出行背景下作为自由度最高的短途出行方式,在混合交通流中仍占据着较大的比重。人车冲突现象增加了安全事故发生的频率,大幅降低了道路尤其是交叉口的使用效率。交叉口是各个方向车流的汇合节点,发挥着重要的交通枢纽作用,然而交叉口也是人车冲突和交通事故的高发地点。交通信号控制是目前道路交叉口交通管理最有效的手段之一。国内外学者对于信号控制交叉口的交通延误做了颇多研究,但关于机动车与过街行人冲突的研究相对较少,尤其是右转机动车与过街行人冲突研究。
Schmidt S和Farber B对行人过街行为进行分析发现,行人过街行为取决于机动车可穿越间隙而非行人过街时间;Lyon C和Persaud B通过分析城市道路交叉口的人流量和车流量,建立了人车冲突预测模型;Ahmed A等对无信号交叉口的机动车右转行为进行分析,探究了引起右转车冲突的重要因素;苏岳龙等通过采集分析右转机动车与行人、非机动车冲突数据,建立了右转车距机非冲突点位置不同时的速度统计模型;陈永恒等根据混合交通流特点计算了行人和机动车在冲突点的通行时间,建立了提前右转的机动车和行人的延误模型;张茂民等通过对行人交通需求进行分析,提出在信号控制和行人干扰条件下的右转车流量控制条件。
Romer等发现当右转机动车与过街行人发生冲突时,通过降低行人绿灯时间、修建地下通道等措施可以降低交叉口机动车延误。根据《中华人民共和国道路交通安全法》(2011版)规定:机动车行经人行横道时,应当减速行驶;遇行人正在通行人行横道,应当停车让行。但从现场调查发现无信号控制右转机动车并未严格遵守让行条例,与行人抢行现象严重。因为在未对右转机动车行为加以约束的信号交叉口,行人过街有信号控制,但右转机动车没有,所以右转机动车抢行时有发生。李玲对右转车辆与行人抢行过程进行分析,推导出了无信号控制的右转机动车直接选择与过街行人抢行情况下的交通延误模型,但并未考虑右转机动车等待一段时间后再与过街行人抢行的情况。该文结合上述研究成果,分析右转机动车与过街行人发生冲突过程,推导右转机动车等待一段时间后与过街行人抢行情况下的交通延误模型,再通过实例分析和VISSIM仿真进行模型有效性验证。
2 右转机动车与过街行人冲突分析
2.1 人车冲突过程
在具有行人信号控制而无右转专用信号控制的道路交叉口,当行人与直行或者转向的车辆在道路交叉口的同一时间、同一地点互相交叉,就会形成交通冲突点。在未对右转机动车行为加以约束的信号交叉口,右转机动车和行人的冲突点有两处,均位于人行横道,如图1所示。右转机动车穿越过街行人时存在以下情况:① 右转车在行人红灯时间内到达,此时行人未至冲突点,右转车可快速通过;② 右转车在行人绿灯时间内到达,但此时无行人到达冲突点,仍可快速通过;③ 右转车在行人绿灯时间内到达,在人车冲突点前停车等待可穿越间隙或者选择抢行。
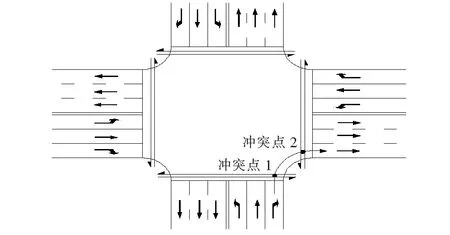
图1 右转机动车与过街行人冲突点
2.2 可穿越间隙
无信号控制的右转机动车在即将到达人行横道前会对行人流进行预判,在遵守行人优先通行的原则下,如果行人之间的间距大于驾驶员预期的最小可穿越间隙,右转车辆就会进行穿越。为了便于分析右转机动车等待一段时间后穿越行人流状态,将过街行人看作独立的个体。假定行人过街状态服从泊松分布,则行人之间的时距大于右转机动车最小可穿越间隙的概率为:
P{h(s)>a}=e-qa
(1)
式中:h(s)为人行横道处过街行人间的时距(s);a为人行横道处右转机动车通过过街行人的最小可穿越间隙(s);q为人行横道处过街行人流量(人/s)。
当过街行人到达服从泊松分布,行人时距就服从负指数分布。故过街行人时距大于最小可穿越间隙时右转机动车可穿越强度λ1为:
λ1=q·P{h>a}=qe-qa
(2)
式中:λ1为单位时间内右转机动车穿越过街行人流时的可穿越强度(人/s)。
2.3 右转机动车等待穿越过街行人流过程
为保证采集数据的统一性,在确定人车冲突的前提下,若在行人绿灯时间内人行横道处行人间距小于最小可穿越间隙,右转机动车仍选择通行,则判定右转机动车抢行。李玲认为无信号控制的右转机动车在人行横道处是否选择同过街行人抢行与最小可穿越距离(最小可穿越时间间隙与行人过街平均速度的乘积,即右转车道宽度)内过街行人的数量高度有关,且右转机动车的平均抢行概率与过街行人数基本呈负线性相关。该文通过观测统计长沙市3个信号交叉口数据证实了上述论断。3个交叉口右转车辆抢行概率与最小可穿越距离内行人数量线性拟合关系如图2所示,基本呈一元线性负相关。
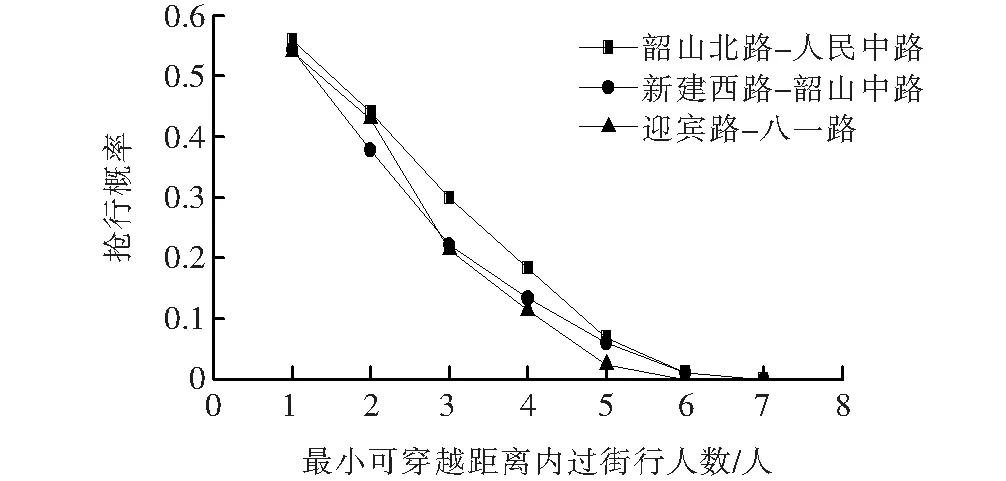
图2 抢行概率与最小可穿越距离内过街行人数的关系
线性回归模型为:
韶山北路—人民中路:
y=-0.094 2x+0.573 8R2=0.946 6
新建西路—韶山中路:
y=-0.105 9x+0.595 3R2=0.939 2
迎宾路—八一路:
y=-0.095 4x+0.570 2R2=0.866 9
从图2可以看出:当道路交叉口最小可穿越距离内过街行人的数量大于一定值时,右转机动车抢行概率为0,可定义该临界值为抢行临界行人数,记作m(整数)。令y为0,可得3个交叉口的x值均不小于7,故可取m=7。
将抢行概率模型通式记作:
y=bx+c(x≤m)
(3)
式中:y为右转机动车抢行概率;x为信号交叉口右转机动车最小可穿越距离内过街行人数,取整数;b、c为相关系数。
当最小可穿越距离内过街人数不大于m时,可以用该线性回归模型计算抢行概率,而当最小可穿越距离内过街人数大于m时,该模型不再适用,但这并不意味着右转机动车不会再发生抢行。事实上,行人过街有成群的现象,前述的右转机动车不抢行准确来说指的是单次到达交叉口最小可穿越距离内的行人数量不小于m时,右转车辆不会抢行。通过现场观测可以看出当过街行人数较多时,部分右转车辆会选择等待一段时间,等行人消散一部分后再抢行。
如图3所示,将临界行人数m看作一个独立的行人群,记作1,将后续抵达交叉口的行人看作独立的个体,记作2,3,4,…,右转机动车遇到超过m个行人后停车等待,将等待时间记作tw,当走在前面的m个行人消散后,右转机动车选择继续等待可穿越间隙或者抢行,回到前述计算模型。当右转机动车遇到超过2m个行人后,模型再次超界,经统计3个交叉口单个行人群中超过2m个过街行人全部通过右转车道的时间超过行人绿灯时间的概率均大于95%,为了便于计算,可认为此种情况下右转车辆不进行抢行,故此时抢行概率为0。
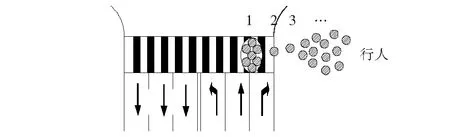
图3 右转机动车等待抢行过程
综合可得抢行概率方程为:

(4)
3 右转机动车延误模型
3.1 不考虑与行人发生冲突的右转机动车延误模型
当无信号控制的右转机动车在到达可能与过街行人发生冲突的区域时,右转机动车若选择等待可穿越间隙,此时会产生交通延误。若选择直接抢行,则在不受其他干扰的条件下不会产生延误。若选择等待一段时间后再抢行,则等待时间需计入延误时间。
在不考虑右转车抢行的前提下,假定行人绿灯时间结束的时间点为0,右转机动车到达与过街行人冲突点的时刻为u,如图4所示。
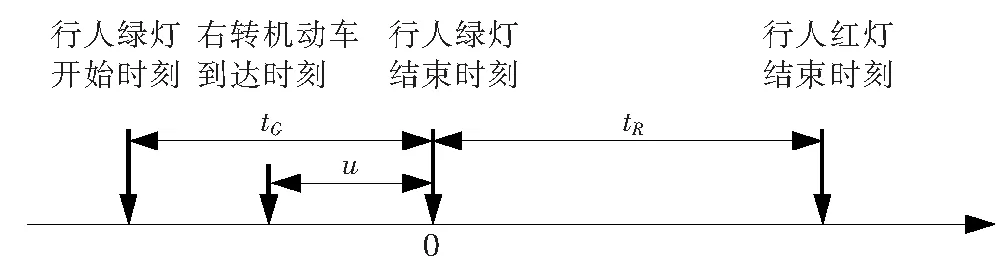
图4 右转机动车到达时刻分布
u的概率密度函数记为f(u),对应的概率分布函数为F(u)。设右转机动车在信号交叉口的延误时间为T,T的概率密度为g(T),对应概率分布为G(T),且0≤T≤tG(行人绿灯时间/s)。
若信号交叉口过街行人到达服从泊松分布,则:
G(T)=p{T≤t}=1-e-λ1t
(5)
式中:T为时间变量;t为机动车穿越行人的临界时间间隙(s)。
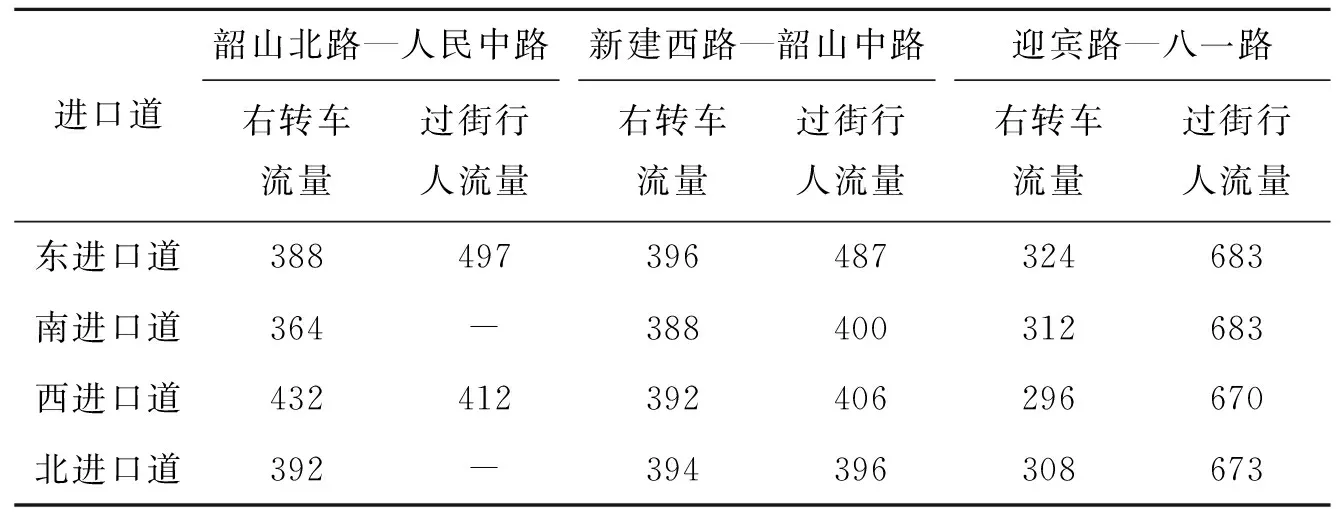
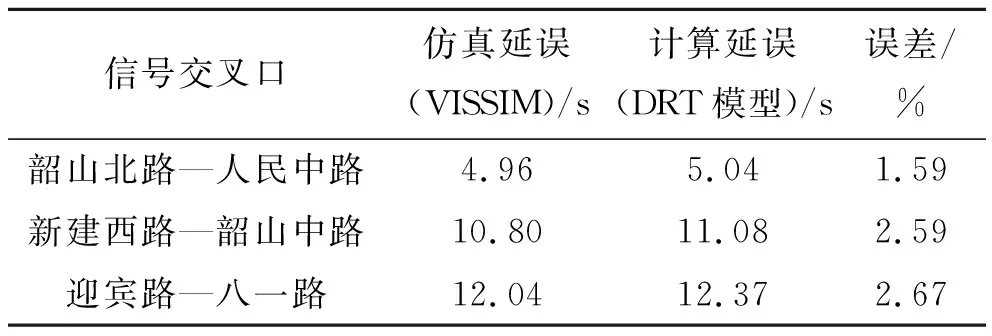
当右转机动车在u时刻到达时其交通延误概率分布密度为g(T,u),对应概率分布函数为G(T,u)。当0≤T 假设右转车到达信号交叉口服从泊松分布,则: f(u)=λ2e-λ2u (6) 式中:λ2为右转机动车在信号交叉口单位时间间隔内的平均到达率(veh/s)。 当过街行人随机过街时间∈[0,tG],在此区间内不考虑与过街行人发生冲突的右转机动车平均延误为: D0=t0+∬tG(t,u)f(u)dtdu (7) 式中:t0为右转机动车加减速损失时间(s)。有研究表明右转机动车加减速延误为6~10 s,该文取其均值t0=8 s。 将右转机动车最小可穿越距离内有1个行人到达的概率记作P1,此时右转机动车抢行概率记作y1,右转机动车交通延误记作D1;那么最小可穿越距离内有x个行人到达的概率为Px,对应的右转机动车抢行概率为yx[根据式(4)可得]、右转机动车交通延误为Dx。 假设过街行人到达服从泊松分布,则在计数间隔t内到达x个人的概率P(x)为: (8) 式中:t为计数间隔,取一个信号绿灯时间(s);λ1的取值见式(2)。 将长沙市3个信号控制交叉口的数据代入发现:在可穿越距离内过街行人数超过2m的概率分别为4%、1.3%、2.4%,在误差5%范围内,为了便于计算,在计算右转机动车交通延误时忽略此部分。则根据概率论求期望值的方法近似计算考虑与过街行人发生冲突条件下右转机动车平均延误为: (9) 若右转机动车在冲突点选择抢行,认为抢行后交通延误为0,根据概率论求期望值的方法近似计算当最小可穿越距离内过街行人数x≤m时右转机动车平均延误为: Dx=(1-yx)D0 (10) 将式(5)、(6)、(7)联立再代入式(10),解得当x≤m时右转机动车平均延误为: Dx=(1-yx)(t0+ (11) 式中:λ1、yx的取值分别根据式(2)、(4)求得。 当可穿越距离内过街行人数m Dx=(1-yx)(D0+tw) (12) 式中:tw为右转机动车停车等待时间(s)。 将式(5)、(6)、(7)联立再代入式(12),解得当m Dx=(1-yx)(t0+tw+ (13) 式中:λ1、yx的取值分别根据式(2)、(4)求得。 以长沙市3个信号控制交叉口为例。其中,韶山北路—人民中路交叉口仅东、西进口道有人行横道,新建西路—韶山中路和迎宾路—八一路交叉口4个进口道均有人行横道。3个交叉口右转专用车道宽度分别为3.2、3.2、3.5 m,每个交叉口均进行两天的高空俯拍录像,每天录制4 h。3个交叉口的绿灯时间分别为60、53、115 s(南北向、东西向为55 s),观测时段为天气条件优良的工作日(07:00—09:00、16:30—18:30)。流量统计见表1。 表1 长沙市3个交叉口高峰小时流量 pcu/h 由表1可计算得韶山北路—人民中路、新建西路—韶山中路及迎宾路—八一路3个信号交叉口右转车等待时间如图5所示。由图5可得:3个交叉口的等待时间算术平均值分别为7.92、10.84、8.45 s。将上述数据代入DRT模型,计算结果如表2所示。 表2 DRT模型计算结果 图5 右转机动车等待时间 张谞博等应用VISSIM对长沙市一信号交叉口进行仿真分析,并与点样本法及HCM2000计算延误值进行比较,发现VISSIM能较好地反映现实信号交叉口的交通特性。因此该文采用VISSIM仿真模型与前述右转机动车延误计算模型进行结果比对。 VISSIM无法仿真右转机动车抢行过程,故需对VISSIM得出的延误值做以下处理: 仿真延误=VISSIM延误值×右转机动车不抢行占比+等待时间×右转机动车等待抢行占比。最终计算结果如表3所示。 表3 仿真延误与计算延误对比 通过分析无信号控制的右转机动车与过街行人发生冲突过程,提出了在考虑右转机动车等待一部分过街行人消散后再抢行的情况下右转机动车交通延误模型(DRT模型)。以长沙市3个信号交叉口为例,进行流量、抢行和等待时间统计并代入DRT模型计算右转机动车平均延误。将模型计算值与VISSIM仿真处理值进行对比,发现韶山北路—人民中路、新建西路—韶山中路、迎宾路—八一路交叉口延误分别存在1.59%、2.59%、2.67%的误差,表明该文模型具有一定的准确性,对于研究右转机动车抢行条件下的交通延误具有一定的参考意义。但该文仅考虑了右转机动车抢行情况,并未研究行人抢行状况,在未来的研究中仍需进一步的改进。3.2 考虑与行人发生冲突的右转机动车延误模型
4 实例计算

5 结语
