下伏岩溶地层隧道的地震响应分析

李明达，张 昱，孟 康，周 晶

(1.大连理工大学 海岸与近海工程国家重点实验室， 辽宁 大连 116024；2.大连理工大学 建设工程学部水利工程学院 工程抗震研究所， 辽宁 大连 116024)

随着我国城市化进程快速发展，为缓解城市交通、运输等压力，各大城市都在大力发展地下空间以满足需求。地下结构一般埋置在围岩中，结构振动受到周围地基的作用，近些年地铁车站、区间隧道，如日本阪神地震、中国台湾集集地震、汶川地震等，均有相当数量的隧道出现不同程度的损伤和破坏，且震后修复难度很大。由此地震作用下隧道结构的动力响应特性受到了国内外越来越多的关注。

由于地下结构地质的复杂性，特别是在岩溶地区的隧道工程，在地震作用下，地层可能会产生较大的变形和位移，使得结构产生严重的损伤甚至破坏，进而将造成巨大的经济损失及人身伤害。现有研究大多关注受溶洞引起的围岩应力、位移变化特点，从施工和静力角度研究溶洞对隧道工程特性的影响，如周华贵等[1]和李鸿博等[2]研究了静力荷载下溶洞对隧道结构内力的影响，并提出了岩溶处理方案及隧道加固方案。齐勇[3]研究了不同位置溶洞对大断面隧道施工力学特性的影响。文献[4-6]通过数值计算及试验研究了岩溶对隧道变形、围岩稳定性及安全距离等的影响，然而目前对岩溶地区盾构隧道的动力响应特性研究较少[7-8]。因此有必要进行岩溶地区隧道工程的地震动力响应分析研究。

本文以大连地铁五号线典型断面为背景，基于黏弹性人工边界理论，建立有限元模型，计算并分析了下伏岩溶地层隧道在不同洞隧间距、洞径大小、溶洞跨径比条件下，隧道结构的地震动力响应特性。研究结果对隧道结构设计、建设及监测具有一定的指导意义。

1 工程概况

大连地铁五号线线路全长24.48 km，其中火车站站—梭鱼湾南站区间(火梭区间)线路全长3 310 m，采用单洞双线大直径盾构隧道建设方案。

火梭区间地质条件较为复杂，区间纵断面地质示意图如图1所示。根据勘察资料，勘察深度范围内主要包括杂填土、粉质黏土、卵石等地层；下部基岩为灰岩、板岩等，且存在辉绿岩侵入岩脉。场地内主要的不良地质作用为岩溶，专勘资料表明，区间内主要存在三个溶洞群，两个溶洞群位于海域段，一个溶洞群位于陆域段。

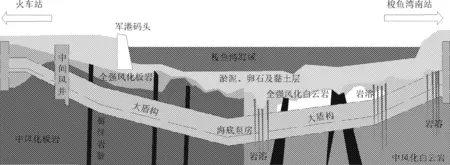
图1 纵断面地质示意图

隧道建设过程中会不可避免的遇到各种复杂地质，岩溶地区通过钻探及跨孔弹性波CT技术得到岩溶类型及发育等情况，但仍可能存在未能探测的隐伏溶洞，在隧道建设过程中会安全通过隐伏溶洞区域，但运营中在动荷载等作用下可能会导致管片开裂、错位、破裂等现象进而造成事故。本工程所处华北地震区中的郯庐地震带，该地震带层发生多次破坏性地震，一旦发生地震，可能对结构造成严重的伤害。

2 黏弹性人工边界及地震动输入

黏弹性人工边界是一种应力型的局部人工边界，具有良好的频率稳定性，能够准确地模拟截断边界外半无限介质的弹性恢复能力，并能有效消除外行波在有限计算区域的截断边界上的反射作用[9]。黏弹性人工边界已经在地下结构中得到了广泛的应用，并且其准确性及高效性也得到了证实[10-11]。本文采用黏弹性人工边界以保证结构系统的地震动输入的准确性，即通过在有限元边界上将地震动波动转化为作用于人工边界节点上的等效荷载。则边界上等效物理体系的弹簧和阻尼系数分别为：弹簧系数：

(1)

阻尼系数：

Cn=ρcp×Ai；Ct=ρcs×Ai

(2)

式中：Kn和Cn分别是弹簧和阻尼器在法线方向上的系数；Kt和Ct分别是弹簧和阻尼器在切线方向上的系数；αn和αt分别为法线方向和切线方向上弹簧的修正系数；R为每一个边界点到力加载点的距离；G和ρ分别为介质的剪切模量和介质密度；cp和cs分别为介质中压缩波和剪切波的传播速度；Ai是边界节点的影响区域。

Liu等[12]提出，在二维黏弹性人工边界中，推荐αt和αn的取值范围分别为[0.35, 0.65]和[0.8, 1.2]。本计算中αt和αn的取值为0.5和1.0。

作用在边界节点上的等效荷载可由下式表示：

(1) 左侧边界上等效节点荷载表示为：

(3)

(2) 右侧边界上等效节点荷载表示为：

(4)

(3) 底边界上等效节点荷载表示为：

(5)

3 模型参数及有限元模型

盾构隧道采用单洞双线双层衬砌方案，由于结构设计中二衬不作为结构受力构件，在本文计算中仅考虑初衬管片。管片内径D1为10.8 m，外径D为11.8 m，环宽2.0 m，管片厚度为0.5 m。隧道围岩结构简化为匀质基岩，且不考虑地下水的影响，结构埋深12 m。研究表明，计算模型取3～5倍跨径时，边界影响较小[14]，所以本模型尺寸横向长度取为84 m，纵向取为68 m。

3.1 模型参数

依据大连地铁5号线火梭区间地质详勘报告，隧道结构穿越地质属于全-强风化白云质灰岩，围岩等级属于Ⅴ级。围岩材料及衬砌结构材料力学参数如表1所示，围岩材料屈服准则采用郑颖人等[15]提出的DP3平面应变摩尔-库仑匹配。

表1 材料力学参数

根据《建筑抗震设计规范》[16](GB 50011—2010) ，大连地区抗震设防烈度为Ⅶ度，设计基本地震加速度值为0.10g，设计地震分组为第二组，选取经修正后的El Centro地震波，峰值加速度(PGA)为0.10g，地震波由基岩底部垂直入射，加速度时程曲线如图2所示。

国内岩溶盾构隧道加固范围一般取距隧道洞径D以内，本文计算中选取距隧道衬砌外缘一定范围内设置溶洞，为简化计算先将溶洞取为圆形，后文将讨论改变溶洞跨径比对结构地震动响应特性的影响。

图2 El Centro波

3.2 有限元模型

数值模拟采用通用有限元软件ANSYS，计算采用地层-结构模型。梁建文等[17]研究中表明，在二维隧道模型计算时，采用PLANE42和BEAM23单元模拟衬砌结构，结果相差很小。故本文计算中衬砌结构与围岩均采用PLANE42单元进行计算。溶洞的数值模拟采用“空场力学模型”计算[18]。根据地勘资料，选取火梭区间内典型断面，建立二维有限元模型。二维模型示意图及有限元模型如图3、图4所示。

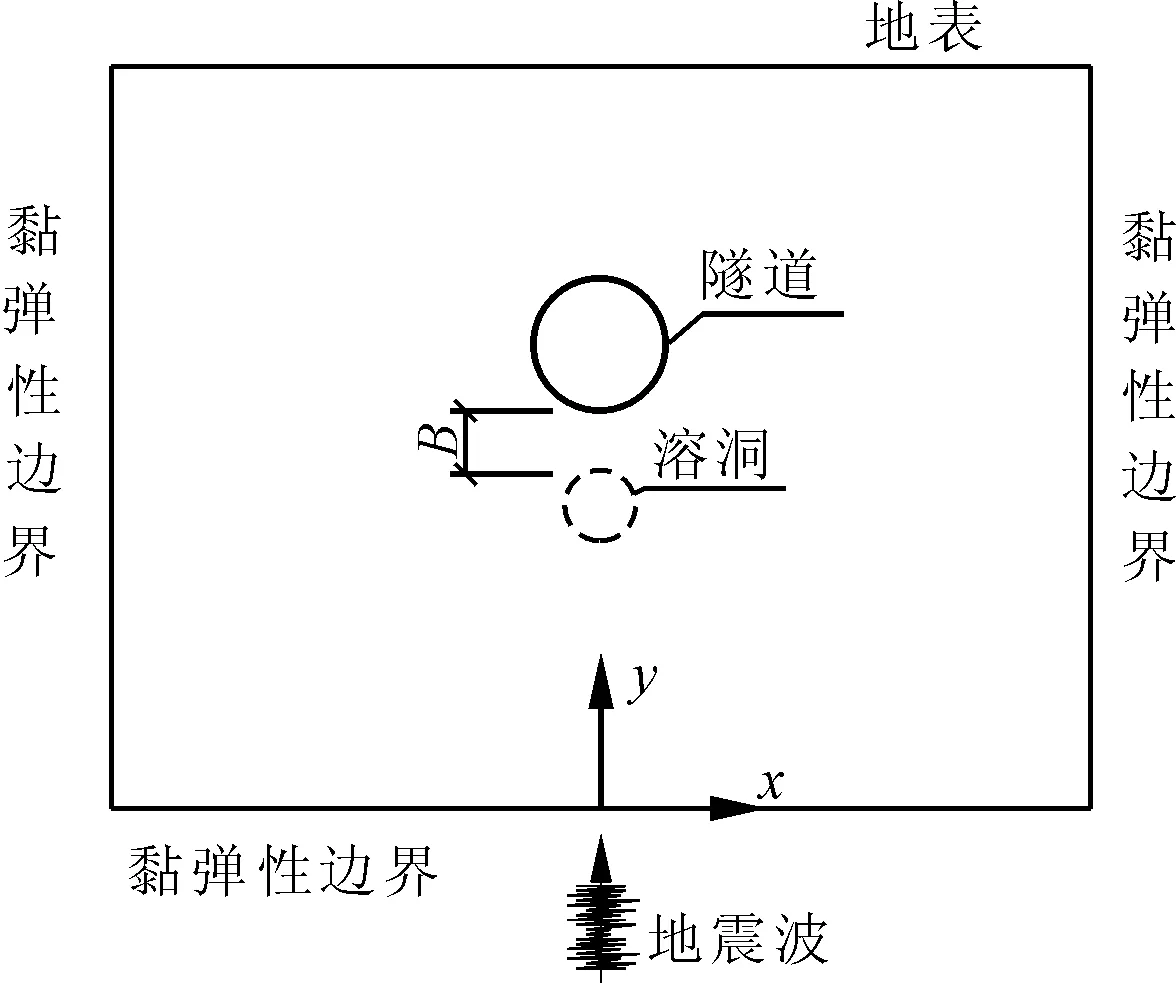
图3 二维模型示意图

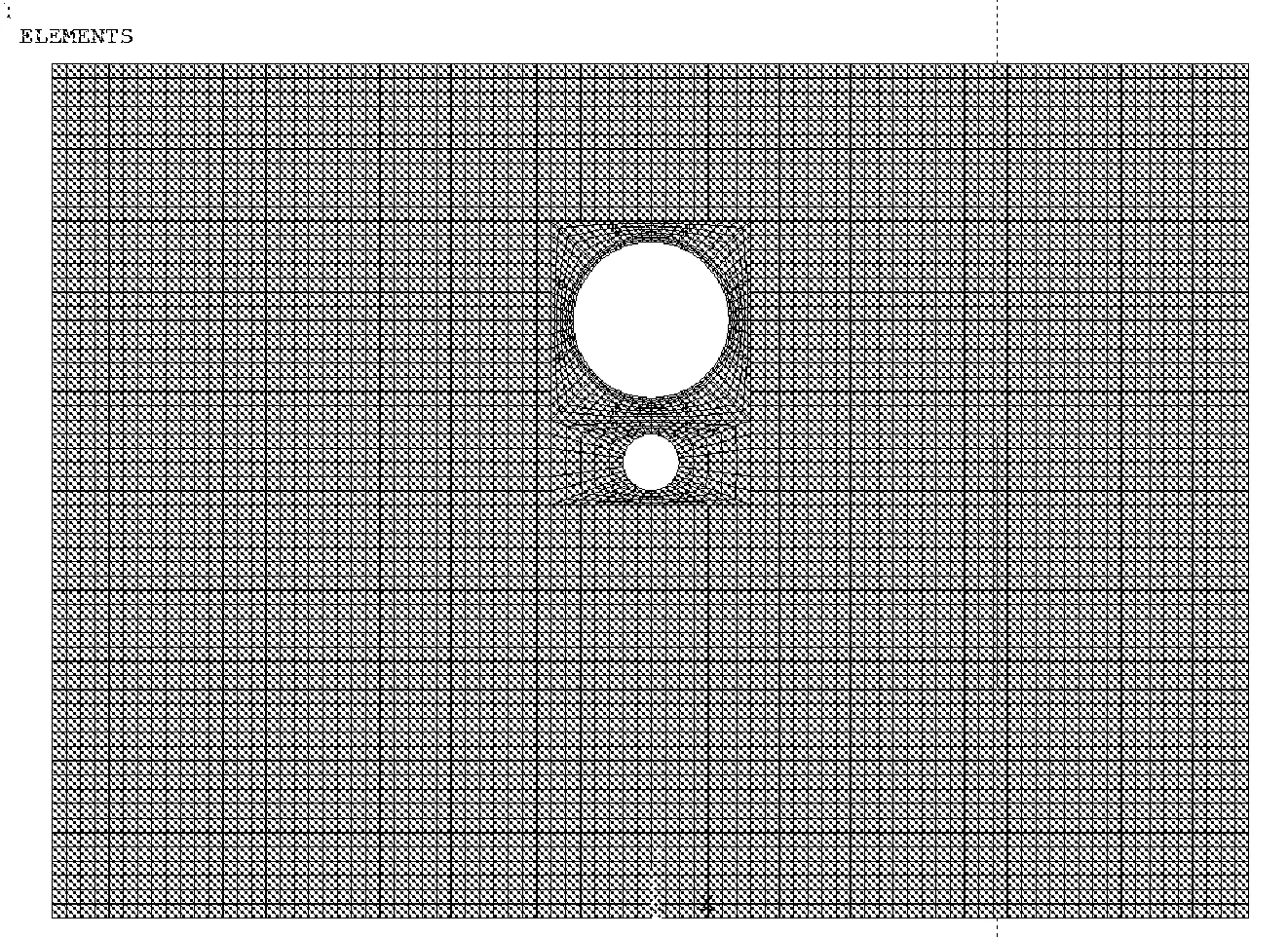
图4 二维有限元模型

模型建立后，首先将整体结构在静力条件下做地应力平衡；其次进行静力开挖模拟隧道形成过程；最后在此基础之上对结构底部及侧向施加黏弹性边界条件，再对整体结构进行地震动分析。结构动力分析中阻尼确定是很重要的，本模型采用瑞利阻尼，按照5%的阻尼比来确定瑞利阻尼的两个比例系数。

4 计算结果及分析

4.1 洞隧间距及洞径尺寸对结构的影响

由于洞隧间距、洞径大小对结构地震响应的影响与隧道直径D有关，通过计算洞隧间距B为0.2D、0.5D、0.8D、1.0D，溶洞洞径0.2D、0.5D、0.8D、1.0D时结构的地震动力响应，得到各工况下结构内缘加速度响应与应力响应。

如图5所示，以洞隧间距B为0.2D的结构加速度响应计算结果为例，与底部无溶洞结果对比，无溶洞时拱底内缘加速度峰值(PGA值)为0.938 6 m/s2，溶洞洞径为1.0D时，拱底内缘PGA值为1.032 2 m/s2，相比无溶洞的PGA值放大了8.6%。由此可见，随着洞径的变大，拱底内缘x方向加速度响应呈现放大效应。

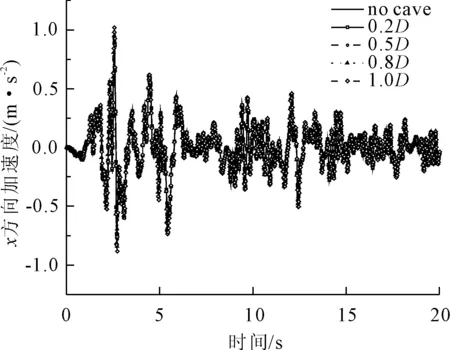
图5 拱底x方向加速度时程曲线

根据各工况拱底x方向时程曲线的PGA值，汇总如表2所示，在洞隧间距一定时，拱底内缘x向PGA值在随着洞径的增大而增大，溶洞洞径一定时，洞隧间距对拱底内缘x向PGA值的影响逐渐减弱。与输入地震波PGA值0.98 m/s2相比，洞隧间距一定范围内，溶洞会减弱结构动力响应，大尺寸溶洞洞径会致使结构拱底内缘x向PGA值呈现放大作用。

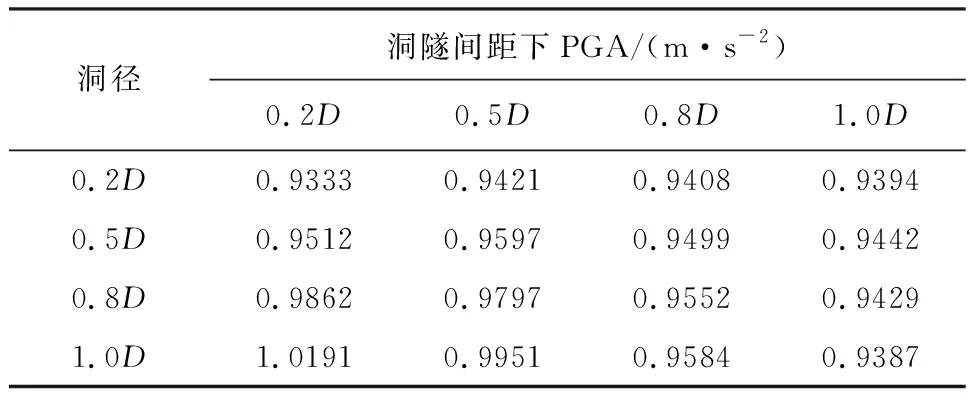
表2 拱底内缘x方向PGA值

以洞隧间距B为0.2D，溶洞洞径0.2D为例，隧道结构内拱顶、拱腰、拱底及同深度位置处围岩的x向加速度时程曲线略有差异，如图6所示。从图中可以看出，在相同深度位置处，隧道结构的加速度响应均略小于围岩内的加速度响应，同深度处围岩加速度响应为1.153 m/s2，比拱顶加速度响应放大1.05倍，比输入地震波PGA值放大1.177倍。从拱底、拱腰到拱顶结构加速度响应PGA值呈现非线性关系，其加速度响应PGA值关系为拱腰(0.798 m/s2)<拱底(0.933 m/s2)<拱顶(1.097 m/s2)。

根据动力响应计算得到各洞隧间距、洞径工况下结构内缘主拉应力峰值包络图,如图7所示。

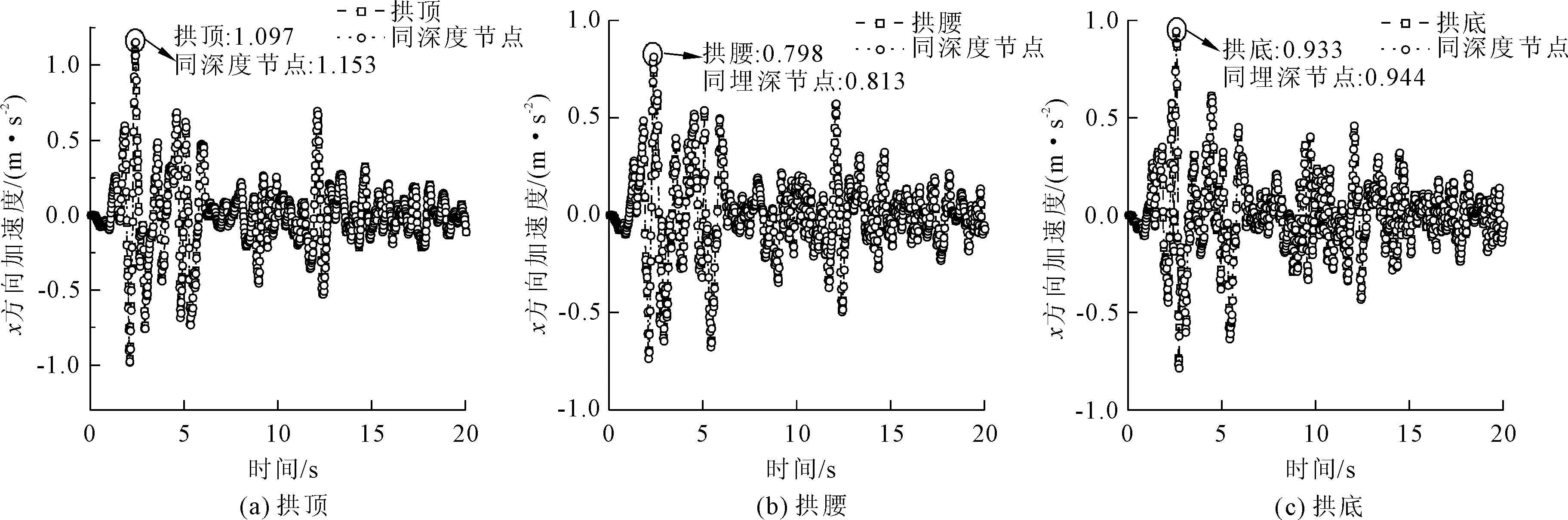
图6 隧道节点及围岩同埋深节点x向加速度时程曲线

受下伏岩溶区域溶洞的影响，各工况下结构下部主应力峰值变化较结构上部更大，随着溶洞洞径的增大，结构主拉应力峰值增幅随之变大，其中结构下部两拱脚附近增幅明显。随着洞隧间距的增大，结构主拉应力峰值增幅越来越小，洞隧间距为0.2D时，主拉应力峰值最大值均出现在结构拱脚附近，与无溶洞条件相比，不同洞隧间距主拉应力峰值增幅倍数最大值分别为2.728、1.363、1.220、1.137，洞隧间距为1.0D时，溶洞洞径大小对结构主拉应力峰值影响基本不大。

图7 不同洞隧间距下结构内缘主拉应力峰值包络图

以洞隧间距B为0.2D，不同洞径下结构内缘主拉应力峰值包络图为例分析，随着溶洞洞径的增大，主拉应力包络图逐渐增大，由于洞隧间距较小，对结构上下部均产生较大的影响，洞径为1.0D结构上、下部主拉应力增幅最大值分别为1.365倍、2.128倍。溶洞洞径为0.2D时，主拉应力峰值增幅较无溶洞时不明显，无溶洞时，拱底主拉应力峰值为0.118 MPa；溶洞洞径为1.0D时，拱底主拉应力为0.233 MPa，与无溶洞相比，放大了0.97倍。由此可见，下伏溶洞对结构拱底影响不明显，对结构拱脚附近影响较大。

表3为各工况下结构内缘主拉应力峰值包络图最大值，当溶洞洞径大小一定时，随着洞隧间距的增大，结构内缘主拉应力峰值逐渐变小，即结构主拉应力峰值与洞隧间距成反比关系，且随着洞隧间距的增大主拉应力峰值最大值增幅逐渐趋于平稳。不同洞隧间距下洞径为0.2D的溶洞对结构主拉应力峰值最大值影响基本不大，在洞隧间距为1.0D时，大洞径溶洞隧结构主拉应力峰值影响不明显。

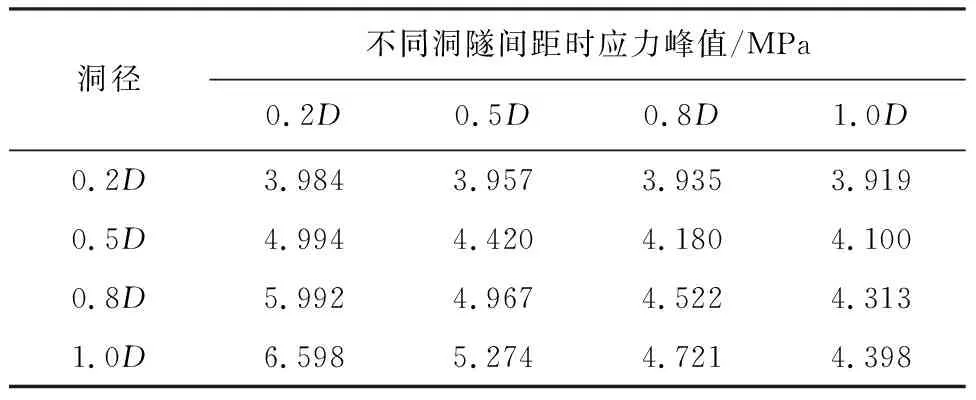
表3 各工况下内缘主拉应力峰值最大值

4.2 溶洞跨径比对结构的影响

上文研究溶洞对结构的动力响应将溶洞简化为圆形研究，如图8所示，以洞隧间距B为0.2D，短半轴长1 m，不同长半轴(L)椭圆形溶洞为例，研究溶洞跨径比(x∶y)对结构动力响应的影响。

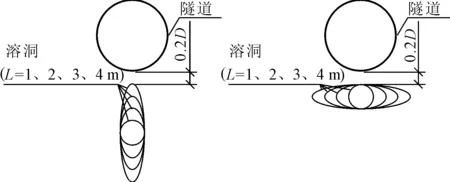
图8 不同跨径比溶洞与隧道空间关系图

如表4所示为不同跨径比条件下结构内缘x方向PGA值，拱腰及拱底均随着长半轴的增大略有增大，无论长半轴在哪个方向，对结构拱顶PGA值的影响效果不明显。长半轴在y方向时比在x方向对结构的影响略大。

根据动力响应计算，得到不同跨径比条件下结构内缘主拉应力峰值包络图，如图9所示。

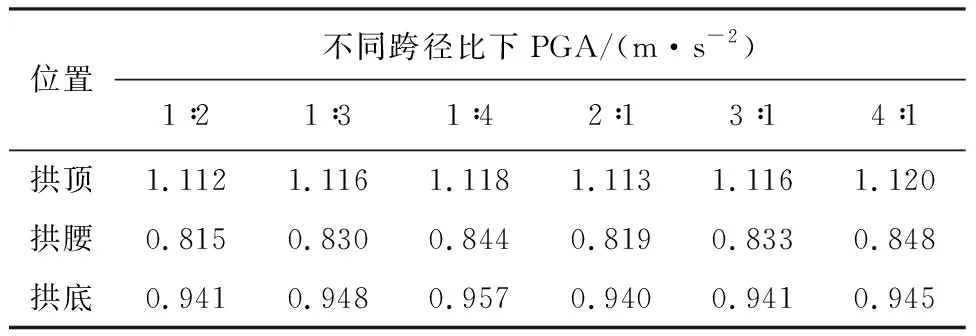
表4 结构内缘x方向PGA值

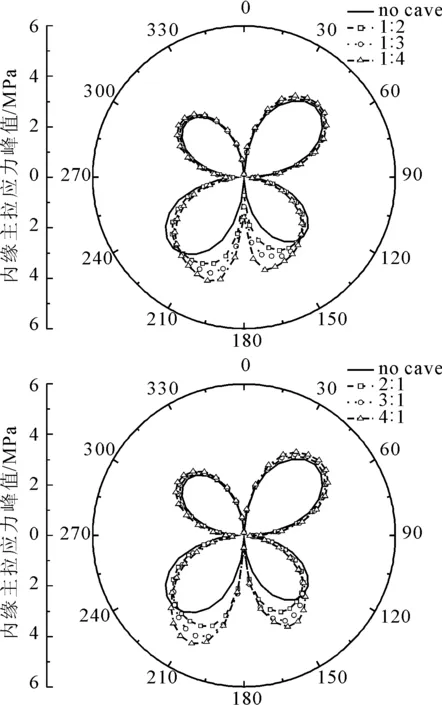
图9 洞隧间距2 m结构内缘主拉应力峰值包络图

从结构整体来看，随着长半轴L的增大，结构下部主拉应力峰值包络图逐渐增大，且主拉应力峰值最大值均出现在结构拱脚附近。

溶洞长半轴在y方向时，随着跨径比值的减小，主拉应力峰值逐渐增大，且结构下部包络图略向拱底收窄，主拉应力峰值在跨径比为1∶4时最大值为4.868 MPa，与无溶洞时主应力峰值最大值3.870 MPa相比，放大1.26倍。

溶洞长半轴在x方向时，随着跨径比值的增大，主拉应力峰值包络图增幅均匀，在跨径比为4∶1时最大值为4.768 MPa，与无溶洞时主应力峰值最大值3.967相比，放大1.23倍。

表5所示为不同跨径比下，结构内缘主拉应力峰值。拱顶主拉应力峰值均在0.075 MPa左右，受洞径比变化不明显，拱腰、拱底主拉应力随着长半轴的增大而增大，长半轴在y方向时比在x方向对结构拱底的影响明显更大。

表5 结构内缘主拉应力峰值

5 结 论

(1) 结构的加速度响应及应力响应随着洞径的增大而增大，随着洞隧间距的增大逐渐趋于平稳，结构及围岩的加速度响应与节点位置深度呈非线性关系，且围岩加速度响应略大于同一深度的隧道结构。

(2) 结构的主拉应力峰值与洞隧间距呈负相关，下伏溶洞对结构拱底影响不明显，且主拉应力峰值最大值均出现在拱脚附近，与无溶洞相比，主拉应力峰值最大放大了2.728倍。

(3) 溶洞跨径比对结构加速度响应和应力响应略有不同，溶洞跨径比对结构加速度响应影响不明显，长半轴在y方向溶洞对结构应力响应影响较大。综合来看，底部溶洞在竖向方向的尺寸对结构地震响应影响较大。

根据本文结果，在岩溶区隧道工程的结构设计应特别加强结构拱脚附近的抗震性能。对大连地铁5号线火梭区间施工及后期运营应加强上述结构部位的监测，采取必要措施加强结构稳定性。