改进传递系数法在边坡稳定性分析中的应用

邓 文 伟

(中铁十八局集团第五工程有限公司, 天津 300459)

边坡是指具有倾斜面的岩土体，是人类工程活动中最基本的地质环境之一。边坡形成时，由于受到自然环境或工程施工的影响，岩土体内部会产生应力重分布，当边坡稳定性较差时，就会发生不同形式的变形与破坏，造成经济损失甚至人身危害。因此，边坡稳定性分析对边坡的治理具有重要意义。

目前，适用于边坡稳定性的分析方法有很多，其中我国规范[1]中推荐的不平衡推力传递法具有适用范围较广、计算方法简便的特点，成为目前国内常用的边坡分析方法[2-4]。但很多学者认为该种方法计算偏于保守，因此展开了大量的优化研究。张晨等[5]针对传递系数超载法对局部条块剩余下滑力小于0的滑坡进行稳定性计算时产生结果偏大的问题进行了研究分析，对传递系数法进行了修正，并通过某滑坡的计算实例证明了修正后方法的准确性。乔梁[6]以宝汉高速某新建隧道为工程背景，通过理论分析、数值模拟和现场监测，研究了隧道洞口顺层仰坡稳定性分析方法和加固措施。将锚索锚固力看作分布力均匀分布在所穿过土条上，此方法改善了应力在滑裂面上集中的问题，土条的实际受力状况得到了更好的反映，使传统传递系数法在加锚顺层仰坡稳定性分析中的计算更加精确。庄晓莹等[7]考虑到锚固边坡具有锚固结构与土体变形协调的特点，在用条分法分析边坡稳定性时由于将土体视为刚体，不能将土体与结构联系起来综合考虑其本质，无法分析周全锚固效应，因此使用了锚固边坡的有限元计算方法。结果表明这种方法所得稳定性系数更大，其有效锚固长度与条分法相比也存在不同。赵晓彦等[8]提出当锚索穿过的滑坡体单元时锚索锚固力应分布均匀，锚固力的作用点为条块中线与锚索相交处。作用在滑动面上的锚固力是沿锚固方向以一定角度从锚墩处向滑动面扩散的分布力而不是单一的力。雷军等[9]为充分考虑锚拉力的应力扩散效应能更合理分析边坡稳定性，将坡面上的锚拉力转化为沿坡面法向与切向的局部条形荷载，与传统计算方法相比，这种方法计算结果偏小，且更接近数值分析结果。

传统传递系数法将锚索锚固力看作集中力，这不符合滑坡体单元的实际受力状况，会造成滑坡的滑裂面应力集中，有必要对此进行改进。因此针对这种弊端，本文提出假设将锚索锚固力均匀分配在锚索所穿过的滑坡体单元上的改进传递系数法，这样更符合实际情况。并以某边坡工程为依托，通过理正软件对天然状态下以及锚固后的边坡进行稳定性分析，并运用MIDAS/GTS软件建立数值计算模型，分析改进传递系数法锚固后边坡位移及应力，以此验证改进传递系数法的可行性。

1 改进的传递系数法

1.1 传统传递系数法

依据条分法的原理，徐邦栋等[10]提出不平衡推力传递法，也称传递系数法。传递系数法是极限平衡分析法中的一种，该法认为岩土体破坏是因滑体在滑动面上滑动造成的，因此将该范围按照岩土体规则划分为多个条块，同时按照条块的平衡条件建立整体平衡方程，并依据该方程进行边坡计算。由滑动面形成的隔离体的静力平衡方程，能够得到沿滑裂面滑动的可能性，即得到滑动面安全系数。不平衡推力法适用于任意形状滑裂面，该法假设条间力的合力方向与上一个相邻土条的底面平行，如图1所示。

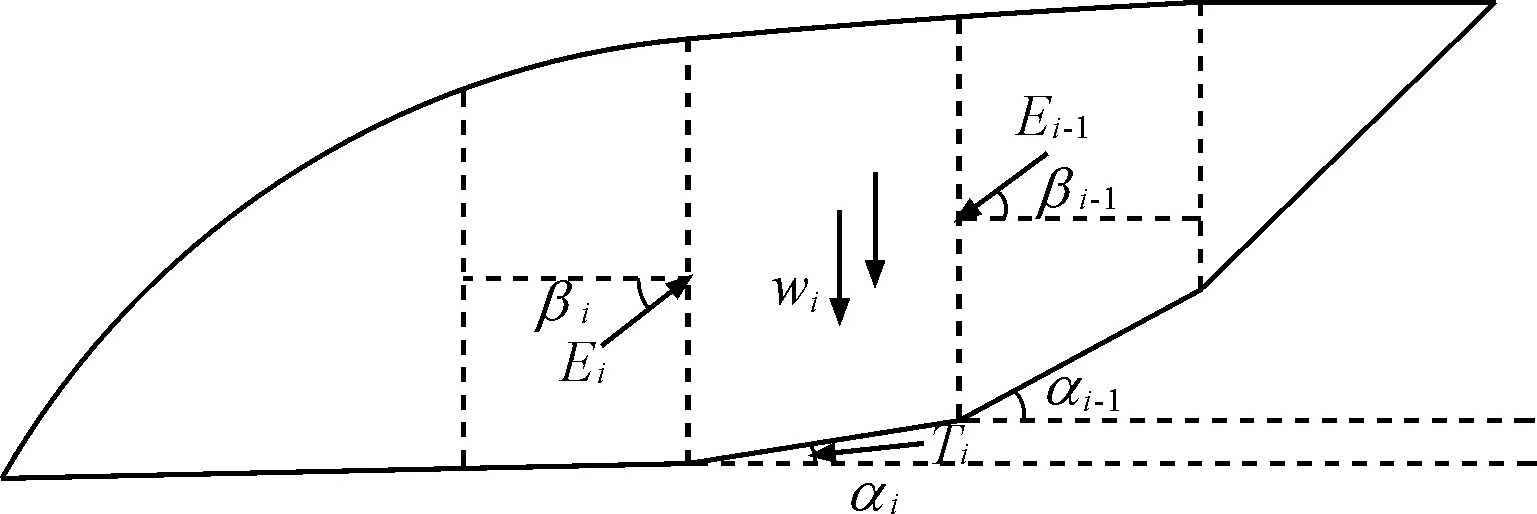
图1 不平衡推力法边坡受力分析图

在图1中，第i块土条自重引起的下滑力为：

Ti=Wicosαi

(1)

式中：Wi为第i块土条自重；αi为潜在滑裂面倾角，(°)。

该土条产生的抗滑力为：

Ri=Wicosαitanφi+cili

(2)

式中：φi为滑裂面处内摩擦角，(°)；ci为第i块土条滑裂面处黏聚力，kN/m；li为第i块土条滑裂面长度，m。

该土条左侧作用于第i块土条的条间力(剩余下滑力的反力)为：

Ei=Ti-Ri+ψi-1Ei-1

(3)

式中：Ei-1为第i-1块土条的剩余下滑力，kN/m；ψi-1为传递系数。

ψi-1=cos(αi-1-αi)-sin(αi-1-αi)tanφi

(4)

从右向左用式(3)逐条计算Ei，到达滑动面终点的条块上有:

En=0

(5)

若假设锚索锚固力为Pu，则第i块土条产生的抗滑力为：

Ri=[Wicosαi+Ei-1sin(αi-1-αi)+Pusin(αi+θi)]tanφi+cili+Pucos(αi+θi)

(6)

式中：θi为锚固倾角。

其中锚索锚固力可由式(2)确定：

Pu=πDLτs

(7)

式中:D为钻孔直径，m；L为锚固段长度，m；τs为注浆体与孔壁之间的极限粘结强度，kPa。

但传统的传递系数法只考虑了滑动面方向的力平衡，而不考虑力矩的平衡条件，在运用中需做出以下补充规定：

(1) 条间力的倾角使条间的剪应力不超过土的抗剪强度。

(2) 条间力不能传递拉应力。

(3) 滑动面所有转折点的倾角变化不应超过10°，否则要进行修正，消除尖角效应。

即便如此，传递系数法同简化Bishop和Morgenstern-Price法比较，安全系数普遍偏大，在工程上不够经济。

1.2 改进的传递系数法

传统传递系数法中，锚索锚固力分布比较集中，未将锚索锚固力均匀分配在锚索所穿过的坡体单元上，如图2(a)所示。针对传统传递系数法在锚索锚固力分布上的不足，可将锚索锚固力均匀分配在锚索所穿过的坡体单元上，即锚索锚固力不作为集中力，而是从锚墩处沿锚固方向以一定角度向滑动裂缝面扩散，如图2(b)所示。改进的传递系数法更适用于实际情况在锚索穿过滑坡体单元时的受力更加均匀，从而提高加锚仰坡稳定性分析中的计算精度。体现了对传统传递系数法的优化。

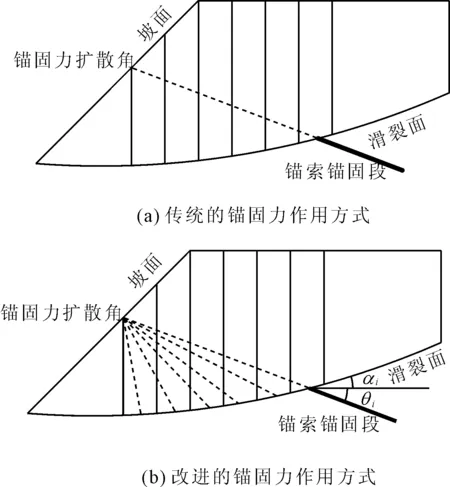
图2 改进传递系数法锚固力作用方式

设锚索水平间距为a，每束锚索的锚固预应力为Pu，第i排锚索锚固角为θi，其穿过处的滑面倾角为αi，第i排锚索产生的锚固力Pi为：

n排锚索能提供的总锚固力为：

sin(αi+θi)tanφi]

(9)

由图2(b)所示预应力的作用方式可知，实际的力量将分布在一定长度的滑动面，而不是集中在一个点上，所以它是合理的，分发一束锚索的锚固预应力通过滑块。在计算过程中，作用点相当于每个滑块的重心。假定第j块土条上共n束锚索穿过，其中第i(i=1,2,3……n)束锚索的锚固力为Pi并且穿过m块滑坡体单元。得到第j块土条所分担的锚索锚固力Pj计算公式为：

(10)

把式(10)代入式(6)得到改进传递系数法的第i块土条抗滑力计算公式：

Ri=[Wicosαi+Ei-1sin(αi-1-αi)+Pjsin(αi+

θi)]tanφi+cili+Pjcos(αi+θi)

(11)

第i块土条的下滑力：

Ti=KWisinαi+Ei-1cos(αi-1-αi)

(12)

式中：K为稳定性计算时采用的安全系数，本文取1.3。

采用改进传递系数法计算加锚后边坡第i块土条的稳定性安全系数为Fsi，如式(13)，即为锚固后边坡整体稳定性安全系数为最后一块土条的稳定性安全系数。

Fsi=Ri/Ti

(13)

Ei=Ti-Ri

(14)

式中：Ei为第i块土条的剩余下滑力。

2 基于改进传递系数法预应力锚索锚固参数设计计算

2.1 预应力锚索锚固力计算

假设边坡中设置k排相同间距的预应力锚索，其中锚索间距为a，每束锚索的锚固力为Pu，锚固倾角为θi，潜在滑裂面倾角为αi，如图3所示。假定第l块土条上共n束锚索穿过，其中第i束锚索共穿过m块滑坡体单元。则第j块土条所分担第i排预应力锚索产生的单位宽度的锚固力Pj为：

(15)

式中：φi为第i排预应力锚索穿过的滑裂面内摩擦角。

图3 边坡加锚图

n根预应力锚索对第j条土体提供的锚固力为：

θi)tanφi]

(16)

其中Pu可由式(7)求得，将式(16)代入式(11)得到抗滑力Ri。

为了使锚固后的仰坡达到稳定，则有：

Pj=Ei=Ti-Ri

(17)

即土体的剩余下滑力等于锚固力，仰坡稳定。

2.2 锚索锚固段位置及锚固段长度的确定

根据《岩土锚杆(索)技术规程》其计算公式为：

lsa=Fs2Pu/πdsτu

(18)

la=Fs2Pu/πdhτ

(19)

式中：Fs2为锚固段抗拉安全系数；ds钢绞线组成锚索体的外表面直径，m；dh为注浆体直径，m；τu为锚索体与注浆材料之间的粘结强度,MPa；τ为锚孔内部岩土体与注浆材料之间的粘结强度，MPa。

每束锚索的钢绞线根数为n，由钢绞线强度和单孔预应力锚索锚固力共同确定：

n=Fs1Pu/Ps

(20)

式中：Fs1一般取值1.7～2.2；Ps为钢绞线极限张拉载荷，kN。

2.3 锚索锚固角度确定

根据《岩土锚固技术手册》锚索最优锚固角计算公式为：

(21)

式中：A为锚固段长度与自由段长度之比；φ为滑裂面内摩擦角；α为滑裂面倾角。

3 工程应用

3.1 工程概况

某工程位于晋、陕、蒙三省接壤地带，黄土高原与毛乌素沙漠的过渡地带。边坡位于阴塔河神庙西北坡，为牵引式基岩顺层边坡，边坡长约150 m，平均宽200 m，边坡高程约60 m。表层主要由砂、泥岩强—中等风化产物构成，两侧上部为黄土，局部为填土，广泛分布于坡体表面，深度5.00 m～7.80 m，平均深度6.65 m，平均厚度6.11 m。下层主要为细砂岩夹泥岩，局部为泥质砂岩，岩层倾角∠60°，中等风化—微风化，是坡体稳定的基座。边坡主要为细砂岩夹泥岩，局部为泥质砂岩。实验得出坡体中的岩石天然重度为21.5 kN/m3～24.8 kN/m3，根据当地的实际岩土及边坡堆积岩体破碎裂隙发育情况，取天然状态下土体的重度为22 kN/m3。该边坡岩土体设计参数如表1所示。

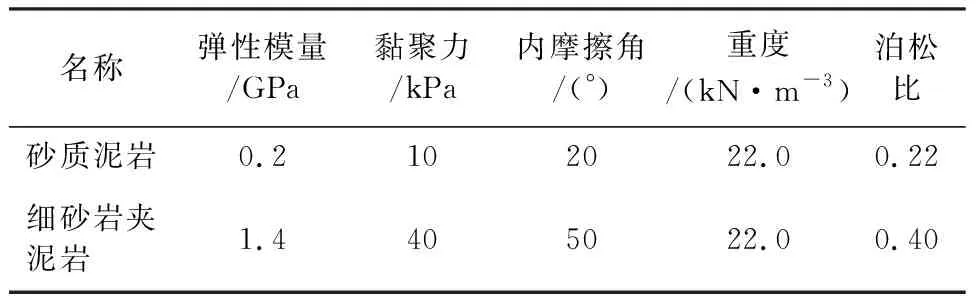
表1 边坡岩土体设计参数表

3.2 边坡稳定性分析

为了计算简便以及考虑计算精确度，将滑坡土体分成8块进行计算。通过理正软件边坡稳定性分析模块计算滑坡稳定性安全系数及下滑力，得到最危险滑裂面位置如图4所示，滑裂面位置即岩土体分界线。计算得到该边坡剩余下滑力为411 kN，稳定性安全系数为0.98，根据《滑坡防治工程勘查规范》[11](DZ/T 0218—2006)第12.4.6条的规定，属于不稳定边坡。

图4 原始边坡滑裂面分析

3.3 预应力锚索加固设计

本工程采用预应力锚索进行加固，锚孔直径φ150 mm，锚索选用强度为1 860 MPa，公称直径为15.24 mm的钢绞线。

根据计算式(18)—式(21)以及《岩土锚杆与喷射混凝土支护工程技术规范》[12](GB 50086—2015)中的规定，设定锚索参数如表2所示。

表2 锚索锚固参数初步计算表

3.3.1 传统传递系数法加锚后边坡稳定性计算结果

由式(6)、式(12)、式(14)计算得到加锚后边坡抗滑力、下滑力、剩余下滑力，计算结果如表3所示，由式(22)计算得到加锚后边坡稳定性系数为1.29。

(22)

式中：ψi为传递系数。

3.3.2 改进传递系数法加锚后边坡稳定性计算结果

传统算法是条块底部滑裂面的倾角为锚索穿过处滑面倾角，而改进算法是以滑裂线与条块中线的交点再与坡脚的连线即为锚索穿过处的滑面倾角。设定锚固间距为3 m，锚索排数21排，由图4可知每块土条上共8束锚索穿过，其中每束锚索共穿过3块滑坡体单元，故每条滑块所分担的锚索锚固力可按式(22)来计算。再根据式(11)—式(14)，计算结果如表3所示。由式(22)得到改进算法加锚后边坡稳定性系数为1.38。

表3 传统与改进传递系数法计算结果

3.3.3 传统与改进算法结果对比分析

由式(22)计算得到两种算法边坡稳定性系数分别为1.29、1.38，改进后的传递系数法偏于安全。由表3可知，改进传递系数法计算的抗滑力相对较大，剩余下滑力计算结果与传统算法比较相对较小。与传统算法相比，改进后的预应力锚索锚固力的分配情况较合理，不会出现应力集中，安全系数合理，可以节约成本。

4 数值模拟

4.1 模型建立及网格划分

MIDAS/GTS是为岩土工程开发的有限元软件，该软件界面简单，具有强大的岩土材料模型库和前后处理功能，能满足大部分岩土体的破坏模式[13-15]。依据工程概况与工程地质手册，模型计算参数如表1所示。所建三维模型长150 m，宽100 m，前部高差40 m，后部高差100 m。边坡岩土体模型建立及网格划分如图5所示。设置锚索21排，锚固间距为3 m，锚索锚固段采用植入式梁单元不需考虑锚固体与岩土体的耦合[16-17]，预应力锚索网格划分如图6所示。用位移法确定了边界条件。在水平方向上，两侧边界都有约束，而在垂直方向上，只约束下侧边界，上边界无约束。分别对传统算法和改进算法加固后的边坡进行数值模拟，在传统算法中对每根锚索施加相同大小预应力，而改进算法中不同位置锚索施加荷载值由式(15)计算所得。

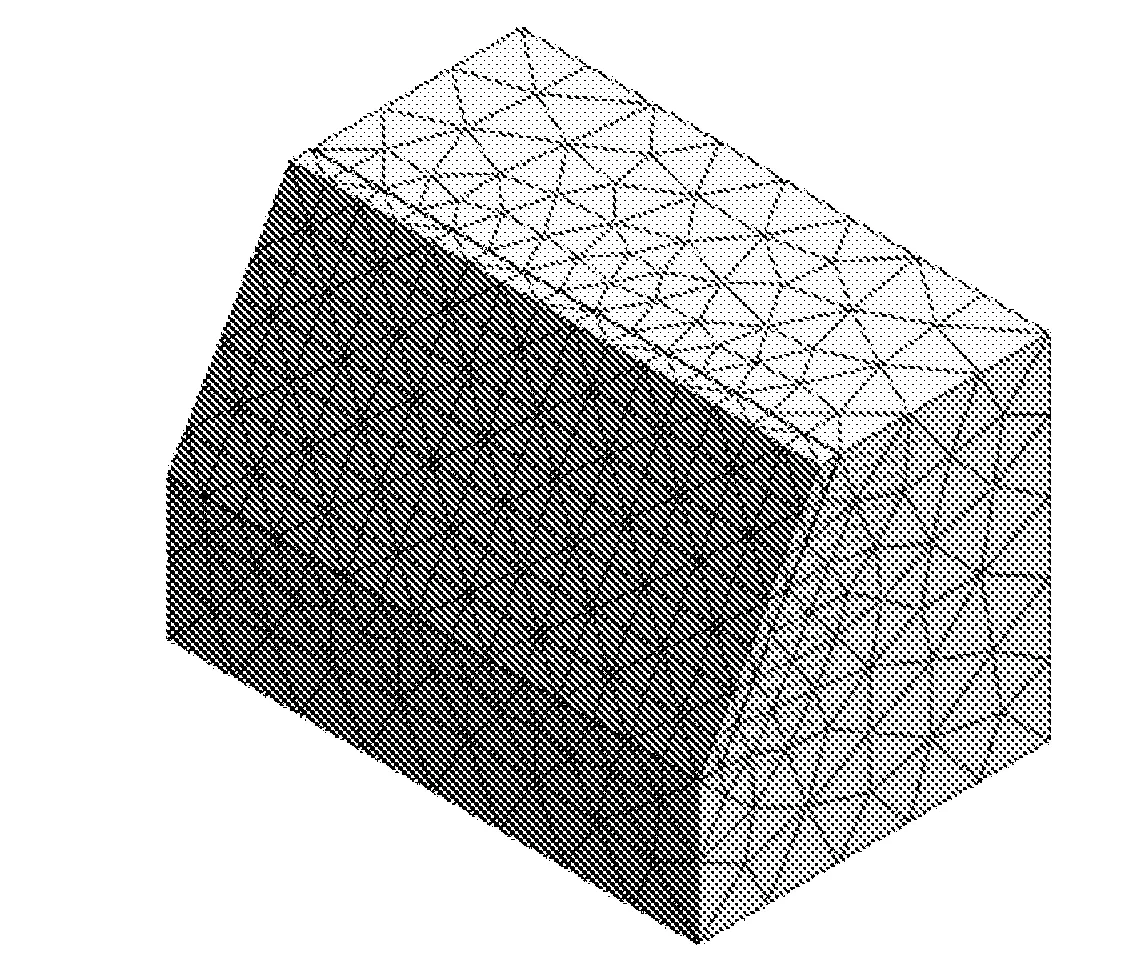
图5 边坡岩土体网格划分图

图6 预应力锚索网格划分图

4.2 计算结果及分析

传统传递系数法模拟结果如图(7)—图(9)所示，改进算法模拟结果如图(10)—图(12)所示，最大位移值，最大主应力值统计结果见表4。通过图(7)、图(10)可知，两种算法下边坡最大位移均出现在坡顶，其中传统算法下坡顶最大位移值为0.083 m，改进算法下的边坡最大位移值仅为0.017 m。对比图(8)、图(11)，改进前后最大主应力值由0.29 MPa降为0.19 MPa，经过计算最大主应力没有超过土体抗剪强度。由图(9)、图(12)可以看出最大剪切变形发生在坡顶，改进算法后最大剪应变值减小，计算结果见表4。以上变化都说明改进后的应力锚索很好的加固了该边坡，有效限制了边坡变形，验证了改进传递系数法在边坡稳定性计算中得可靠性。

表4 数值模拟计算结果表

图7 传统加锚后边坡总位移图

图8 传统加锚后边坡最大主应力云图

图9 传统算法下边坡最大剪切应变云图

图10 改进后边坡总位移图

图11 改进后边坡最大主应力云图

图12 改进后边坡最大剪切应变云图

5 结 论

(1) 本文提出的改进传递系数法假定锚索锚固力沿锚固方向扩散，即锚固力均匀分散在锚索穿过的每个土体上，这样可使滑坡体单元的应力分析更加符合实际。

(2) 通过工程实例验证了改进后的传递系数法较传统传递系数法相比既可确保工程安全，又可以节约成本。

(3) 运用 MIDAS/GTS 有限元分析软件对加锚后的边坡进行数值模拟，进一步证实了改进的传递系数法在加锚边坡稳定性分析及在边坡稳定性分析中使用预应力锚索加固的准确性和可行性。