铝蜂窝叠层板锯切刀具机构模型改进分析
2021-05-13李飞,陈琳,肖雨,李楠
李 飞,陈 琳,肖 雨,李 楠
(1.北华航天工业学院 机电工程学院,河北 廊坊 065000;2.河北省跨介质飞行器重点实验室,河北 廊坊 065000;3.北华航天工业学院 科技处,河北 廊坊 065000;4.北华航天工业学院 计算机学院,河北 廊坊 065000)
铝蜂窝夹芯子料[1-2]的蜂窝夹层结构,以其高比强度、高比模量、尺寸稳定性广泛用于航天器、空间站、卫星、飞机、高速列车、轮船等领域。铝蜂窝芯是由多层铝箔粘合、叠压成铝蜂窝叠层板[3-4],使用时先切成需要的条状,然后展开成规则的蜂窝形状。铝蜂窝叠层板在实际的高精度直线锯削[5-6]加工过程中却存在加工振动问题,造成切割断面直线度下降,噪声较大[7],不能满足现实的生产需要。
目前很多科技人员对锯片振动特性方面进行过研究,如郭兴旺博士[8-9]做过圆锯片振动模态分析的纯理论分析,主要推出无量纲函数,并得到函数的数值解;沈宇峰等[10]做过锯片铣刀的计算机模态仿真分析,使用abaqus软件仿真出锯片的前8阶振型模态,并得到62.94 Hz~68.78 Hz为低阶模态密集区;赵民等[11]做过金刚石圆锯片在实验条件下的横向振动分析,得出圆锯片转速过大时,圆锯片会产生较大的横向振动,并随转速增大而增大;谭心等[12]通过对两种不同的锯片施加相同的横向载荷并进行瞬态的动力学仿真,得到了锯片横向振动响应曲线。但是也都停留在自由振动的理论分析和实验分析上,针对铝蜂窝叠层板力学特性[13]是各向异性,加工切削振动[14-15]时,必然不是开始就为自由振动,而是瞬时静力状态下的受迫振动,随之进入衰减状态。本项目主要针对铝蜂窝叠层板锯切加工过程中的锯片振动做理论分析,希望能通过薄板小扰度理论分析找出造成切削振动的具体理论模型,通过matlab数值计算得出其参数对切削振动的影响趋势,并结合实际的工程进行分析和实验,找到能应用于工程实践的刀具机构模型,即在保证精度的前提下,能够降低维修成本,并提高锯片使用寿命,使之能够适用于切削同类材料通用特性的刀具机构模型。
1 理论分析
切割所用锯片的尺寸是305 mm×3.0 mm×25.4 mm×120,锯片外圆直径为305 mm,内孔直径为25.4 mm,刀片厚为3 mm,整圈刀齿数120个。可以看出锯片厚度远远小于外圆直径(δ/r<1/6,r为锯片的外半径,δ为锯片厚度),实际观察其振动挠曲与板厚的比值w/δ<1/5,w为锯片扰度,可以认为是薄板小扰度进行数学建模。
在实际生产中发现切削振纹在入刀处和出刀处较为明显和密集,可以认为锯片在短时间内受到一个较大的横向起振力,然后进入平衡力状态的振动衰减。所以薄板锯片的平衡力状态下的振动微分方程为
(1)
式中:
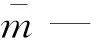

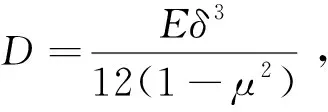
t—时间变量。
设方程式(1)的解为
w=(Acosωt+Bsinωt)W(r,θ)
(2)
式中:
ω—振动频率;
A,B—待定系数;
W—相应的振型函数。
将解(2)式带入微分方程(1),得出振型函数的微分方程:
▽2▽2W-γ4W=0
(3)
式中:
γ—替代符号,其替代公式为
(4)
此时取振型函数为如下形式:
W(r,θ)=R(r)cosmθ
(5)
式中:
m=0,1,2,……—周向波数,即节径数,沿坐标θ方向均布,m为0时振型是轴对称;
R(r)—只关于半径变量r的函数。
将式(5)代入式(3)得
(6)
微分方程(6)的解为
R(r)=Cm1Jm(γr)+Cm2Im(γr)+Cm3Ym(γr)+Cm4Km(γr)
(7)
式中:
Jm、Ym、Im、Km—分别为m阶第一、二类及第一、二类修正贝塞尔函数;
Cm1、Cm2、Cm3、Cm4—待定系数,其值则有边界条件确定。
将式(7)代入式(5)得到完整的振型函数:
W(r,θ)=[Cm1Jm(γr)+Cm2Im(γr)+
Cm3Ym(γr)+Cm4Km(γr)]cosmθ
(8)
实际的锯片形状如图1,此处不考虑锯齿的影响,因为齿高远远小于半径值,在理论模型中非主要矛盾,故忽略。内半径为a的圆孔安装在侧铣刀柄上(刀柄型号为BT40-SCA25.4-75),所以内半径为a处的边界条件可以看成固定边,半径b处为切削刀齿处,边界条件可以看成自由边。
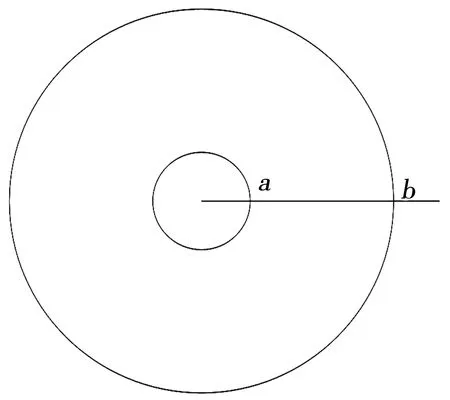
图1 切割锯片简图Fig.1 Sketch of the cutting blade
由以上分析可以得出,r=a处为固定边,则边界条件为扰度和斜率为0,即
(9)
r=b处为自由边,弯矩和横向剪力为0,即
(10)
(11)
将式(8)代入式(9)、(10)、(11)。并应用贝塞尔函数递推关系进行简化,得到如下的公式:
(12)
其中,四个方程分别是
Cm1aJ+Cm2aI+Cm3aY+Cm4aK=Cm1J(γa)+Cm2I(γa)+Cm3Y(γa)+Cm4K(γa)
(13)
Cm1bJ+Cm2bI+Cm3bY+Cm4bK=
(14)
Cm1cJ+Cm2cI+Cm3cY+Cm4cK=
(15)
Cm1dJ+Cm2dI+Cm3dY+Cm4dK=
[(m-1)Jm(γb)-γbJm+1(γb)]}-
[(m-1)Im(γb)-γbIm+1(γb)]}+
[(m-1)Ym(γb)-γbYm+1(γb)]}-
[(m-1)Km(γb)-γbKm+1(γb)]}
(16)
如果想要齐次方程有非零解,则系数行列式的值应该等于0:
(17)
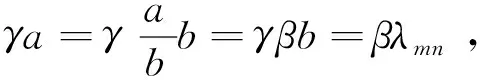

表1 参数表Table 1 Parameter table

图2 节圆为0时,夹径比与无量纲频率的关系Fig.2 When the pitch circle is 0,the relationship between the diameter ratio and the dimensionless frequency
2 工艺分析
从以上的理论分析可以看出,增大锯盘内外半径的比值能够增大锯片的频率系数λmn,而频率系数λmn与各阶频率值成正比,所以改变了锯片的固有属性,使锯片的动刚度增大,而锯片的动刚度直接影响锯片在受到轴向冲击后的横向振动。所以较好的锯片模型应该是圆带状,但其不能直接应用于工程中,以下通过分析来设计满足工程应用的刀具模型。
增大锯片内外半径的比值的方法:
①减小锯片的外圆尺寸,即换一个比较小的锯片;
②增大锯片的内孔直径。
方法①虽然增大了内外半径的比值,但是减小了锯片的外圆直径,根据公式(18)可以知道当转速一定时,切削速度跟刀具的直径同向变化,当锯片的直径变小时,切削速度必然变小,造成达不到加工铝合金工件的高速切削速度。
(18)
式中:
v—切削速度;
d—锯盘的外圆直径;
n—切削转速。
方法②,增大锯片的内孔直径,必然会带来侧铣刀柄直径变大,使整体的空转功率增大,而且锯片的内孔直径是有相应标准的,如果采用非标准锯片,对于锯片这种切削易损工具,一定会带来加工成本的直线增加。
通过以上分析,可以看出方法①和方法②都不是理想的解决办法,而理论分析时,假设内孔的边界条件为扰度和斜率为0,即满足式(9)即可,所以改进的刀具模型机构满足边界条件即可,为了其能进行工程应用,先将整体的刀具模型机构进行拆分,由三部分组成,即刀片、前护刀盘(如图3)、后护刀盘(如图4)。当护刀盘夹住刀具时,护刀盘的外径可以看成刀具的内径,此种刀具模型即满足了理论分析,也符合加工工艺的需求。

图3 前护刀盘Fig.3 The front of blade guard

图4 后护刀盘Fig.4 The back of blade guard
3 加工实验
3.1 实验器材
根据以上分析,进行实际的加工实验。实验所用工具:一台自研制的铝蜂窝叠层板的切割机,所用刀柄为BT40-SCA25.4-75,切削所用锯片为305 mm×3.0 mm×25.4 mm×120 mm,护刀盘的直径为
180 mm,其夹径比0.59、大于0.5。实验所用铝蜂窝叠层块的铝合金材料牌号为5A02-HX8(LF2Y),规格为0.03 mm×4 mm×1 500 mm(350层),即是铝箔厚度为0.03 mm,蜂窝芯格边长为4 mm,板长1 500 mm。所采用的切削工艺参数:切削速度为1 916 m/min,进给量为10 mm/s。实验过程如图5所示,刀盘位置如图6所示。

图5 切削实验简图Fig.5 Sketch of cutting experiment

图6 刀盘安装位置Fig.6 Installation position of cutter head
3.2 实验结果分析
图7、图8为刀具机构模型改进前后切削的铝蜂窝叠层块的实物图。从图7可以发现改进之前入刀处发生切削振颤的非稳定切削,在已加工工件表面留下了较大的刀具痕迹,表明切削振动的振幅较大,随着刀具的z方向进给,系统经过一段振荡过程,进入了稳定切削状态,符合理论分析的自由振荡的条件假定。较深的振颤刀纹的存在,不仅影响工件的表面粗糙度,还会造成工件尺寸的急剧变化,使已加工工件在距离料头和料尾150 mm的两处工件报废,增加原料成本。

图7 改进前切削的工件Fig.7 Cutting workpieces before improvement
图8为改进之后切削加工的工件。可以发现改进之后的入刀处也有切削振颤的非稳定切削,但是切削振动的振幅明显较小,已无明显的振纹痕迹,这是由于增大了锯片内外圆的半径比值,提高了振动模态的各阶固有频率,有效避开了共振区域,使振动幅值明显降低,且衰减明显在一个较小的范围,增加了加工的工件可用区域,提高了材料的利用率,符合理论分析的结果,达到了预期的目的。

图8 改进后切削的工件Fig.8 Cutting workpiece after improvement
用德国Mahr数显游标卡尺(量程为150 mm,分辨力为0.01 mm)测量改进前后工件尺寸(理论切削尺寸为25 mm),测量点位置如图9,得到的尺寸如图10、图11。可以看出改进前其尺寸误差为0.20 mm,改进后其尺寸误差为0.04 mm,尺寸精度提高了一个数量级,且尺寸相对稳定。通过观察和测量都可以发现,改进后的刀具机构模型可以解决实际的工程问题,且改造成本可以接受。

图9 工件测量点位置Fig.9 Measuring points of workpiece
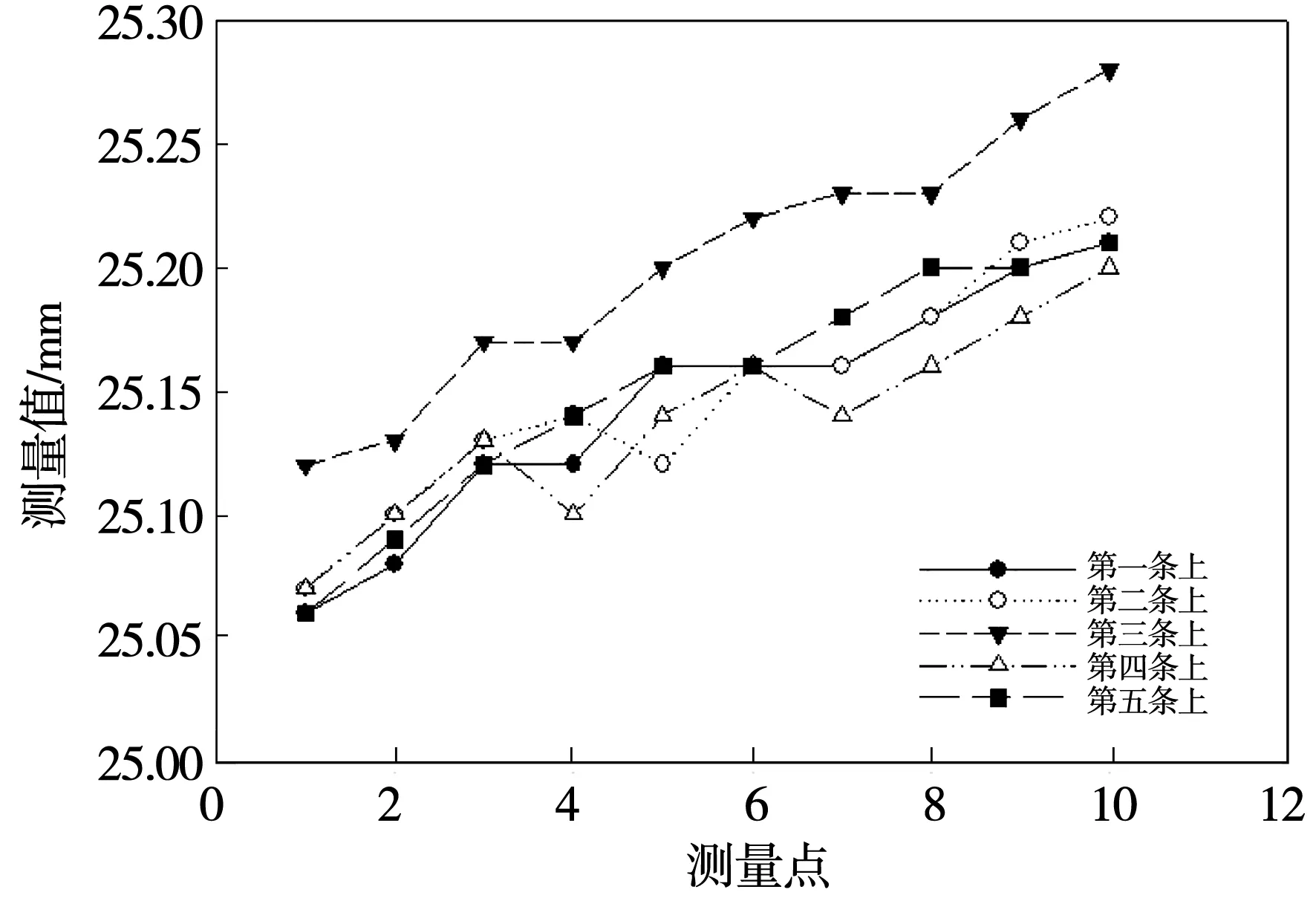
图10 改进前的测量尺寸值Fig.10 Measurement size before improvement

图11 改进后的测量尺寸值Fig.11 Measurement size after improvement
4 结 论
通过以上的理论分析和工艺分析,以及实验的结果可以看出:
1)提高锯片内外径的半径比值,可以有效地提高锯切过程中振动模态的各阶固有频率,提高了锯片动刚度。
2)锯片的内外圆的半径比实际是按分析的边 界条件所确定的,不必是圆环上的半径值。
3)工艺分析中是通过增加护刀盘来提高内外圆半径比值,这其实带来了装刀和卸刀的效率降低,但是在换刀频率十分低的情形下,增加的装刀和卸刀时间是可以接受的,且可大幅度降低维修成本。
4)从理论分析到工程的实际应用时,应考虑在成本允许下的所有可能性,最终选择相对合理的改进方案。
