交通拥堵判别方法研究综述

贾若 戴昇宏 黄霓 李水滢 刘志远

(东南大学 交通学院，江苏 南京 211189)

在国家、城市发展中，经济发展与交通建设一直密不可分。近年来，我国经济的高速发展，使城市交通出行需求急剧增加，但城市基础设施建设速度较为滞后，无法满足快速增长的出行需求，交通拥堵已成为城市交通运输中最常见的问题之一。交通拥堵是一种车多拥挤且道路上车辆行驶速度缓慢的现象，国内外每年因交通拥堵产生了大量的经济损失，且造成能源浪费以及环境污染。为了有效地减少拥堵的危害，各国学者都致力于缓解以及消除交通拥堵的研究与实践，而这其中关键的一步便是交通拥堵的判别与分析。

国外学者自20世纪50年代起，就开始了对交通拥堵现象的系统研究。从传统的交通流理论方法到新兴的与计算机等学科交叉的机器学习方法，各国学者已经进行了许多有效的探索。国内对于交通拥堵判别的研究虽然起步较国际落后，但我国学者根据国内的实际情况进行了拓展与创新，进一步推动了交通拥堵判别与分析理论的发展。

国外的研究通常采用研究交通异常事件的方法对交通拥堵进行判断，我国通常采用道路占有率、排队车辆及交通流速度作为城市交通拥堵的检测标准，通过对道路通行能力、占有率等交通参数进行阈值判断，综合评判城市道路是否产生了拥堵。在交通拥堵自动检测中，当某路段在一定时间内，道路占有率、交通流速度和交通量等多个参数均超过阈值时，才认为存在交通拥堵[1]。传统交通流理论的模型，通常使用传统物理学、数学等基础学科的理论描述交通行为。模型虽然合理简单、有明确的物理意义，但其限制条件多[2]。相比之下，机器学习使用数据驱动方法，深入挖掘数据信息，对于异常特征及其特征变化十分敏感，同时更为注重模型的应用价值和算法研究[3]。这类模型主要用于复杂交通流现象的研究，其中，一些机器学习方法能够更好的检测交通异常事件，并更好地获取车流速度、道路占有率以及是否有拥堵车流等特征的变化，能够被用于交通拥堵判别。

文中主要从传统的交通流理论方法和机器学习方法中归纳总结交通拥堵判别方法。文中的主要内容包括：交通流理论方法中的基于指标方法、基本图方法、元胞自动机模型(CA Model)、元胞传输模型(CTM Model)以及二流理论(Two-fluid Model)。在机器学习部分，依次介绍了贝叶斯理论、马尔科夫这两种基于概率图模型的方法，还介绍了支持向量机、K-近邻、神经网络、聚类等非参数统计方法。最后对现有的传统交通流理论方法和机器学习方法进行总结，并指出一些有待解决的研究方向。

1 传统交通流理论方法判别拥堵状态

1.1 基于指标的方法

交通拥堵最直接体现是出行时间的增加和车辆行驶速度的下降，但各国对交通拥堵尚无统一的定义，也没有统一的衡量标准[4]。自20世纪50年代起，国外相关科研机构开始对交通拥堵评价体系进行研究，提出了近百种用于评价交通拥堵状态的指标。对于路网中交通流速度降低、交通瓶颈的出现及车辆占有率增加等情况，研究者们通常根据多次实验结果为各指标设定某一阙值，将模型的实际运行结果与阙值进行对比，进而判别拥堵状态。其中传统拥堵状态判别的指标可分为基于出行时间的指标、基于排队论的指标、基于公路通行能力手册(HCM)的指标。不同指标适用于高速公路或城市道路等不同场景下的交通拥堵判别。在此基础上，研究人员对不同指标进行组合，衍生出许多更加有效的基于指标的拥堵评价模型。

1.1.1 适用于高速公路的指标

(1)行程时间与延误

行程时间与延误是评价高速公路是否拥堵的有效指标。行程时间通常由地点车速或浮动车法调查得到。延误是指因道路条件、天气、排队或者交通管制等各种因素引起的行驶时间的损失，表现为车辆通过某一段路时实际行驶时间与理想行驶的时间差[5]。

美国国家高速公路合作研究项目根据行程时间定义交通拥堵，将其分为可接受拥堵与不可接受拥堵[6- 8]；其中当行程时间大于自由流下的正常行程时间，且所形成的延误时间较大时，即认为发生拥堵，当延误超过民众接受范围时即为不可接受拥堵。

(2)占有率

占有率包括时间占有率与空间占有率。空间占有率表示某一时刻某一路段内，车辆总长度与车道总长度之比，表明道路实际占用情况；但道路的空间占有率很难直接得到，因此往往很少应用。时间占有率代表任一道路上所有车辆通过该段的累计时间与所有车辆观测总时间的比值，反映了该路段车辆的排队时间。根据道路交通流理论，车流密度小时车速快，时间占有率低，车流密度大时车速慢，时间占有率高。

美国芝加哥交通管理部门规定，车道占有率高于30%并且该状态维持的时间超过5min时即为交通拥堵。Koukis等[8]对比分析了多个临近周期的占有率数据，并将结果与阈值对比进行拥堵判断；国内学者庄斌等[9]采用交通流量与占有率的增量变化率对交通拥堵状态进行判别。

(3)服务水平

服务水平通常根据平均交叉口延误及V/C比进行判断，美国交通管理部门根据V/C比将公路服务水平分为6级，当其大于0.9时处于不稳定流状态，稍有干扰即处于拥堵状态；日本与我国分别实行对应的三级、六级公路服务水平分类方法。

除此之外，区间平均车速也用于高速公路交通拥堵的判断，例如公路通行能力手册(HCM)当中使用区间平均车速计算高速公路交织区服务水平判断拥堵。区间平均车速需要特定地区长期的大量数据统计结果，不具有普适性，但不同地区可根据实际情况自行制定对应标准，判断拥堵状态。

1.1.2 适用于城市道路的指标

(1)区间平均车速

区间平均车速可以更好的体现出车辆在某一特定的时间及路段上的行驶状态[10]，该指标不仅能够反应每辆车各自的交通行为，同时能够随着实际的交通供给与需求状态改变而变化[11]。某一特定路段上的区间平均车速也可利用该区间长度除以此路段上所有车辆的平均行程时间。

日本道路公路团对城市快速路的拥堵定义为，当某一城市快速路段上车队以低于40 km/h的速度行驶或反复多次停驶，并持续该状态15 min及行驶1 km以上即为拥堵[12]；在2002年，我国公安部出台规定，根据城市主干路的区间平均车速对交通运行状态进行描述，定义区间平均车速低于30 km/h时的道路处于拥堵状态，低于10 km/h时为交通严重拥堵。德国学者Kerner[13]基于经典交通流理论提出了三相交通流理论，并以区间平均速度区分交通自由流与拥堵状态，发现拥堵交通流中的车速低于自由流中的最低车速；北京工业大学交通工程北京市重点研究室[14]通过数据采集、利用默认阙值降噪处理数据，类比三相交通流理论，运用统计分析方法得出交通流速度低于30 km/h时进入拥堵状况。

(2)排队长度

排队长度指自交通间断点，排队或低速行驶的车辆占有的道路长度。排队长度越长，拥堵越严重，该指标反映的拥堵情况直观而易于理解。我国规定，3个信号周期车辆未能通过交叉口即为阻塞。当交叉口进口处排队延长到上游交叉口时，此时车辆的排队长度不能准确评价交通拥堵状态。

排队长度比表示停车线上游排队长度与停车线至上游交叉口停车线长度之比。若排队长度比在低于0.5下的某一值附近浮动时，排队长度小，交通较为流畅；若排队长度比趋近于1，则排队即将溢出，交通拥堵严重。

(3)流量比通行能力(V/C)

流量比通行能力指理想的道路交通条件下，最大服务交通量与基本通行能力之比，也称道路负荷度，即V/C比。由于一个V/C比的值通常对应两种相反的交通状态，一般不单独用于交通拥堵评价，而是与其他参数共同组成评价体系。

20世纪80年代末，Lindley[15]将实验中获取的高峰小时交通量扩样为日交通量，使用V/C比对交通拥堵进行评价，若该值大于0.77时，认为道路处于拥堵状态；Cottrel[16]提出AADT/C的概念，美国加州35个城市规定了当V/C比超过1.0或者AADT/C超过9.0时即发生了拥堵[17]。焦海贤等[18]提出虚拟路网容量均衡分析模型，考虑道路供需矛盾关系以V/C比为指标判别城市交通网络中的交通瓶颈，为缓解城市交通拥堵、保障城市交通资源供需平衡提供了新思路。

(4)平均交叉口延误

平均交叉口延误是高峰行驶期间，所有车辆在交叉口延长度内行驶的实际时间与在该路段内以自由流速度行驶时间的差值的均值，该值能够将拥堵量化，较为准确地评价交叉口拥堵情况。

对于城市道路，流量比通行能力(V/C)在评价城市道路通行状况、公共交通运行状况等方面有着广泛应用。在城市道路中，使用平均交叉口延误及V/C比评价道路服务水平。但相比高速公路服务水平，城市道路服务水平尚且没有统一理论，徐林等[19]定量划分了北京的城市道路通行能力，初步探索了城市道路服务水平分级方法。

1.1.3 综合指标判断拥堵

相比上述采用单一指标对交通拥堵状态进行判别，许多复杂情况下的拥堵判别需要采用多种参数进行判断，将各种不同的指标组合在一起，通过系统的模型与算法对交通拥堵进行判别。

2007年Hartgen等[20]通过对不同地区的大量历史数据分析，提出了出行时间指数(TTI)与超负荷车道长度(LMO)的拥堵指标。其中出行时间指数(TTI)是由行驶时间与自由流下行驶时间的比值定义的拥堵判别指标，超负荷车道为流量通行能力比大于等于1.0的车道。Bertini等[21]在2004年，利用俄勒冈州过境交通区的公交调度系统数据与车辆自动定位(AVL)数据获取了行驶时间和速度两种指标，以此分析交通运行状态。该研究有助于过境机构或交通研究人员更好的进行干线性能评估；Coifman等[22]在AVL数据中获取了出行时间与平均速度，定量分析了交通流的情况；Bertin等[23]在2005年，利用伦敦附近环路探测器的数据，进行了高速公路车道缩减处的交通流特性研究，采用时间平均速度、占有率等指标，探讨了排队消散流量与排队形成流量之前的关系，通过计算交通波的传播速度，判断交通拥堵开始和持续的时间。

在道路服务水平的评价中，通常根据平均交叉口服务水平及V/C比两个指标进行判断。在交通流理论中，交通量由行驶速度及车辆密度共同确定，当三参数均处于理想状态时，交通流处于临界状态，一旦车的数量有所增大，交通流量便会减小，同时行驶速度减小，交通流密度增大，该段道路便被判定为拥堵状态。

不同单一指标以不同方式组合在一起，可以衍生出许多种行之有效的拥堵状况综合评价模型。与单一指标下的拥堵判别相比，综合判断指标适用范围更广，判断判别的结果也更加可靠。上述指标也常作为机器学习方法的参数，利用机器学习模型与方法，能够更准确地捕捉指标特征的变化，且更有效地利用交通数据，从而更好地判别交通拥堵。基于指标判别拥堵的重要参考文献汇总如表1所示，将排队论瓶颈值和交通流参数的变化进行量化，通过单一指标和综合指标对交通拥堵进行判别。

1.2 基于宏观基本图的分析方法

上述基于指标的方法，通常用于判别局部路网的拥堵情况，实际应用中具有相对的局限性。随着人们对交通拥堵的研究从局部区域逐渐转移至整个路网，宏观基本图方法也逐渐被提出。

宏观基本图(MFD)的概念最早由Daganzo和Geroliminis[24]提出，并且他们在后续的研究中给出了宏观基本图的定义，被认为可以用于描述城市道路网中移动车辆数量与道路网络运行水平之间的一般关系。宏观基本图模型通过统计分析路网的历史数据，得到不同参数之间的关系，从而得到宏观基本图模型。通常包括密度-速度模型、流量-速度模型和流量-密度模型。其中，最具代表性的密度-速度模型由Greenshields[25]在20世纪30年代提出。

根据MFD理论[26]，现有两种具有代表性的宏观基本图相关参数计算方法，其一为

(1)

式中:kw为城市路网范围内的加权密度;ow为其加权时间占有率；i为路网中路段编号；li为路段i的长度；qi为路段i的车流量；s为路网中行驶车辆的平均长度；oi为路段i的时间占有率；ki为路段i的密度。

还有一种方法为

(2)

式中，N为分析的路段或者检测断面数量，k为路网的平均密度，v为路网的平均速度，q为路网的平均流量。

1.2.1 宏观基本图在城市道路拥堵判别中的应用

Daganzo等[27]于2001年在日本横滨，使用主干道上的固定传感器与出租车载移动传感器，记录车辆占有率及车辆行驶状况，并于2007年提出了宏观基本图的概念。Buisson等[28]于2009年在法国图卢兹市，利用线圈检测器监测路网中的交通流运行数据，根据得到的MFD显示，路网中宏观交通量随密度的变化概率与路网中检测器与停车线的距离成正比。贺正冰等[29]在2014年利用北京市快速环路上分布的交通监测器，利用宏观基本图的思想，研究得到路网密度分布的不均匀性与网络流量的函数关系有相同的变化趋势。通过分析快速环路的交通拥堵变化规律，得出该特征的原因是北京市快速环路拥堵的传播过程是中心向外辐射的过程。

1.2.2 宏观基本图在高速公路拥堵判别中的应用

Saberi等[30]，在2012年利用波兰高速公路网的数据，研究了拥堵判别中信号控制对宏观基本图造成的影响与滞后性。姬杨蓓蓓[31]在2013年研究采用Vissim仿真实验，根据实测数据建立并标定了阿姆斯特丹高速公路的仿真模型。通过对不同车道临界密度的定量分析，量化了路网拥堵情况，并通过交通仿真使用MFD模型描述了路网交通拥堵的变化过程。Gavah等[32]，于2011年提出，MFD模型只适用于高速公路网实施了交通管制措施的情况，如采取匝道控制、可变信息情报播报等。因为MFD良好应用或者得到光滑的宏观基本图的前提，是交通拥堵较为平均的分布在被测路网中，而这需要一定的交通管制措施。

运用监测手段获取路网数据，进而绘制城市路网宏观基本图，虽然在宏观基本图与交通拥堵的研究中被广泛适用，但通常因成本较高与数据缺失，难以得到完整宏观基本图，对深入分析有一定影响。因此目前大部分关于宏观基本图的研究均采用交通仿真获得所需数据。交通流的基本图方法能够比较直观地体现交通拥堵形成的原因与过程，但是由于阈值的难以界定，在实际使用中往往有较大的局限。宏观基本图的分析方法文献整理如表2所示。

表1 基于交通拥堵指标的重要文献

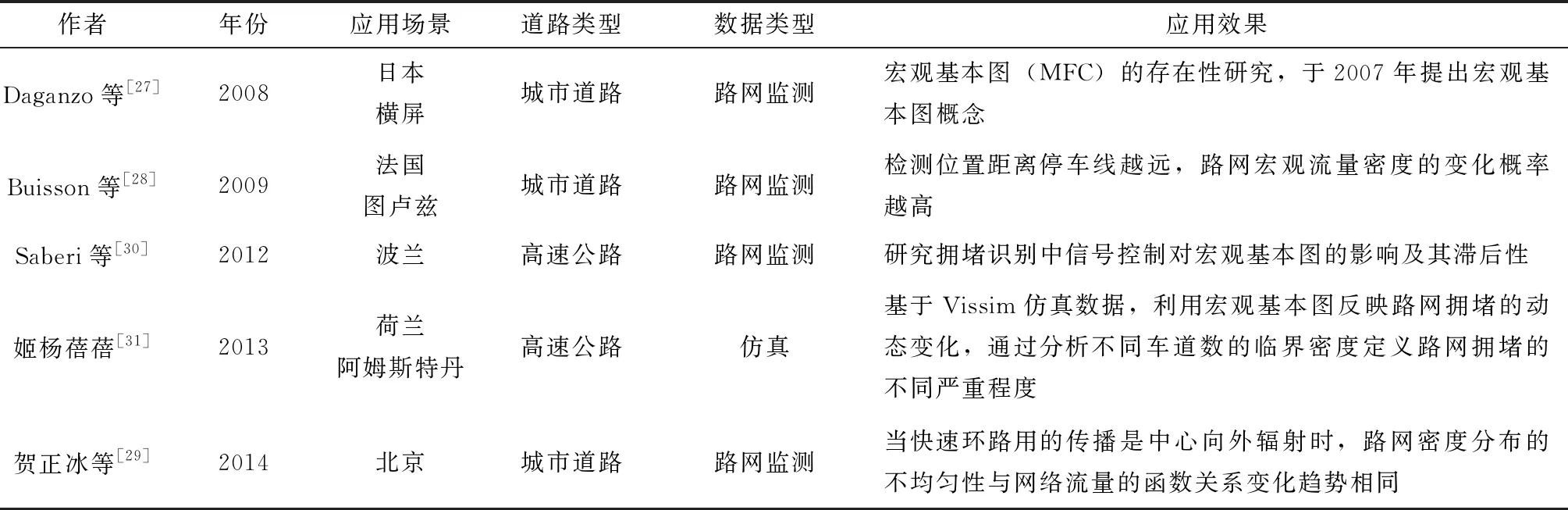
表2 宏观基本图模型与应用

1.3 元胞自动机模型(CA Model)

元胞自动机是粒子在一个由具有离散、有限状态的元胞组成的空间上，按照某种局部规则在离散的时间维度上演化的动力学系统模型[33]。元胞自动机理论最初由“计算机之父”冯诺依曼提出，并在20世纪90年代起成为了道路交通流领域的热点研究方向，可以用于拥堵的判别与评估。

最初用于交通研究的一维元胞自动机模型模拟的是单车道的交通状况，其中最具代表性的是在Wolfram[34]的元胞自动机规则基础上建立的一维模型(NS)[35]。

该模型将一条单车道用一个一维点阵表示，每个位置点代表一个元胞，其中空置或容纳一辆车，运行状态取决于元胞是否空闲或者车速大小的不同，同时所有车辆按照特定的速度规则和位移规则运动，模拟真实的交通状况。

NS模型设置了一种较为理想的车辆运行条件，能反映出车辆的启动和停止过程，表现出交通流的拥挤和非拥挤状态，对交通拥堵的判别有一定作用。但考虑到城市道路往往交错形成路网，一维元胞自动机模型无法更细致地表现其交通特性，因此基于二维元胞自动机的模型(BML)[36]应运而生。

BML模型首先给出了一个二维周期性边界的正方形网络，每个格点上空缺或者存在仅向东或仅向北行驶的车辆。不同方向的车流在奇偶时间步上错开运行，若某一辆车的前方格点上有车，则该车不运行。

BML模型考虑了交通信号灯因素下的情况，但只模拟了交叉口情况而忽视了路段，并且车辆只能在两个方向上行驶，仍然与实际的交通状况有很大区别。

为了改正这些问题，城市交通网络模型[37](CS Model)在BML模型与NS模型结合的基础上应运而生。并且在此之后，各国学者都致力于BML模型的扩展与衍生。如Nagatani等[38- 40]分别在考虑了立交桥的设置、车辆的不对称分布情形以及车辆的转向情况后建立了新的元胞自动机模型等。

总之，元胞自动机模型形式简单，且易于在计算机上模拟、实现。该模型不仅能够得到每一辆车的微观特性，而且能表现交通流的宏观特点，从而进行交通拥堵的判别。然而，元胞自动机的研究虽然比较深入，理论也较为全面，但比较缺乏真正的应用，因此在实际应用中还需要进一步的检验。

1.4 元胞传输模型(CTM Model)

LWR(Lighthill-Whitham Richards)模型是一个交通流一阶流体动力学模型，可以用以下方程来表示：

(3)

式中，Q为交通量，x为位移，k为密度，t为时间。

LWR模型从流体力学的角度较好地描述了交通流特性，但是由于其求解过程比较复杂，并没有被很好地实际应用，因此知名学者Daganzo[41- 43]在此基础上提出了元胞传输模型。

元胞传输模型(CTM模型)在经典的LWR方程的基础上进行了分段线性化处理，并将道路划分为多个等距离的元胞，时间也同样离散为多个时间间隔，原本的方程化简为如下的离散形式：

(4)

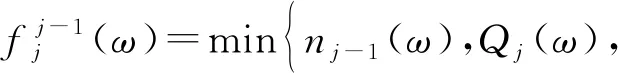
(5)

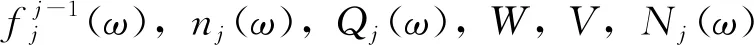
通过这样的离散形式，LWR模型所描述的交通流现象得到了较好的数学解法。因此CTM模型能够重现与实际交通流情况接近的现象，并进行拥堵的判别与分析。

后来，Daganzo又在考虑车流滞后效应的因素后提出了迟滞元胞传输模型(LCTM)，该模型具有更高的计算精度[44]。在此后的时间里，其他各国学者也在他的研究基础上进行了大量研究，先后提出了ELCTM模型、MCTM模型、SSM模型、ACTM模型、CCTM模型与LSCTM模型等[45]，一步步提高了模型的普适性与准确性，使其与真实的交通状态特性越来越接近。

由于元胞传输模型与实际交通情况的良好拟合特性，其常常被用在交通拥堵机理的研究上，也在实践中被用于交通拥堵的判别与分析。元胞自动机模型和元胞传输模型的应用整理后列于表3。

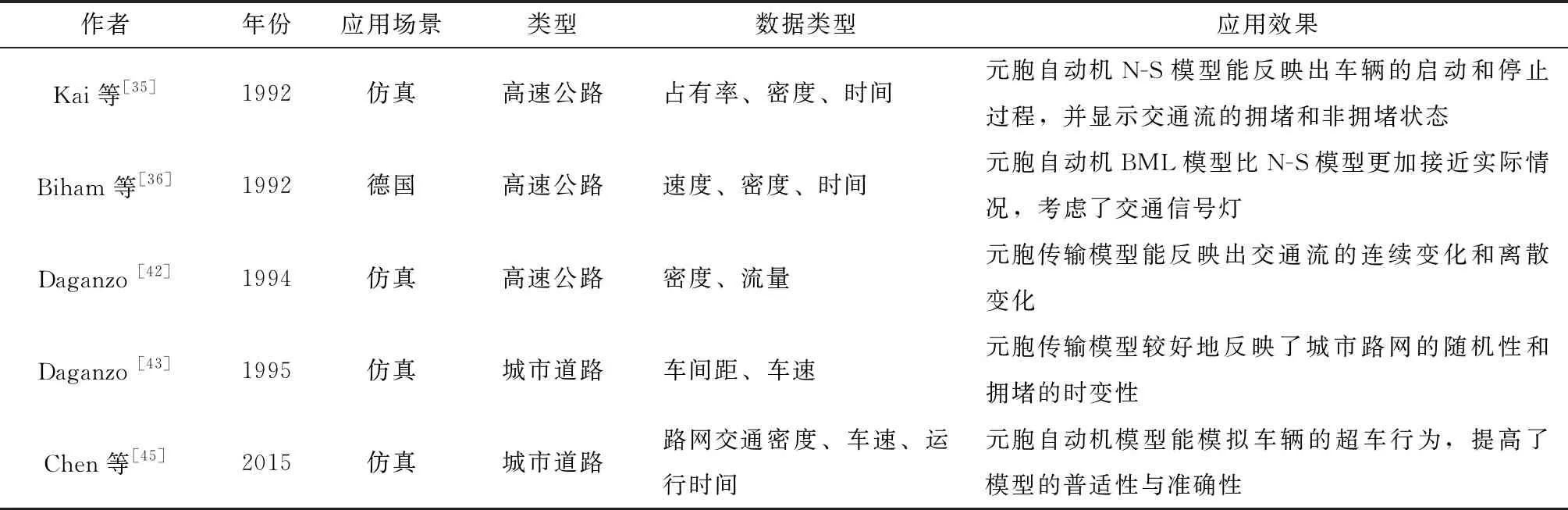
表3 元胞传输与元胞自动机模型的应用

1.5 二流理论

除了LWR模型和CTM模型利用流体力学的理论知识进行交通流的研究外，交通领域的研究者们从20世纪中期开始一直都在尝试着用动力学理论描绘交通特性。

为了避免对不同的交通状态下的细节进行分类讨论,Herman等[46]在动力学理论的基础上提出了二流理论，将交通流中存在的车辆分为运动和由于交通原因停止的两类，并作出了如下两个结论：①路网中车辆平均速度与运动车辆在整个交通流中所占的比重成正比；②路网中每单位距离的车辆行驶时间与单位距离的停车时间呈现线性相关趋势。此后，Herman等[47]又在德克萨斯州的奥斯汀市进行了一系列实验，除了证明上述两个结论的正确性外，还提出了：③路网中循环测试过程时测试车的平均停车时间与整个路网中的停车时间相一致的假设。

此后，这一理论被证明除了在路网中成立外，还在城市干道及其各部分、各时间段下成立[48]，并且被用在了城市道路服务水平的评价上。张翛等[49]建立了基于二流理论的城市干道交通模型，并提出了一个评分函数来对其服务水平进行评价。王殿海等[50]从二流理论出发，对城市路网中宏观层面的交通参数之间的关系进行了推导，由此建立了对宏观交通状态进行评价的模型。

总之，二流理论由于其适用的广泛性，在各种交通状况下都可以直观简单地使用，并且不需要考虑各个过程的细节问题。因此，使用这一理论分析交通状态，进行交通拥堵的判别往往能收到良好的效果。

2 机器学习方法判别拥堵状态

传统交通流理论模型运用数学和物理学的定理来描述交通流特性，以分析的方法阐述交通现象及机理。但是数学和物理的模型并不能完全正确地描述现实复杂交通流。机器学习模型可以很好地克服此局限，它们没有固定结构约束，被证明与数据有更好的拟合[2]。利用机器学习方法判别拥堵的研究文献整理于本章末尾的表4中。

2.1 基于概率图模型的方法

建立概率图模型也是常用的判别交通拥堵，预测交通流状态的一类方法，其中具有代表性的模型包括贝叶斯网络、马尔科夫模型等。

2.1.1 贝叶斯网络

(1)贝叶斯网络简介

贝叶斯网络从形式上看是一个有向无环图，以结点表示变量，有向边表示结点之间的关联关系，边的权值为条件概率(设起点为A，终点为B，则有向边的权值为P(A|B))。

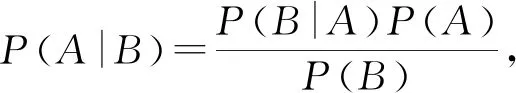
(2)传统贝叶斯网络的构造

构造贝叶斯网络的过程主要分为3步。

步骤1 确定变量集和变量域

步骤2 确定变量间拓扑关系，形成网络结构

建立网络结构最常见的方法就是从主观的经验出发(通常是依据专家知识)，根据变量间的因果关系建立网络结构，例如盛春阳等[51]在使用贝叶斯网络对交通状态进行预测时，通过变量关系图建立模型的网络结构，直接获得网络结构，但缺陷是主观成分较大。现在也有学者从数据的相关性分析出发，探索变量间的依赖关系，例如Liu等[52]学者在建立贝叶斯网路结构时，采用定向依赖式分析的方法，通过计算两个变量之间的条件独立性来确定两个节点是否需要用边来连接(即变量间是否存在关联关系)，然后再采用基于条件交互信息的碰撞判别来确定边的方向。

步骤3 确定贝叶斯网络的概率分布

如图1所示，要想求得目标——交通状态的值，必须确定贝叶斯网络的概率分布。确定概率分布的方式常常是从已有的数据和经验出发得到先验概率，然后通过样本训练得到后验分布，多次迭代，得到最终的概率分布。

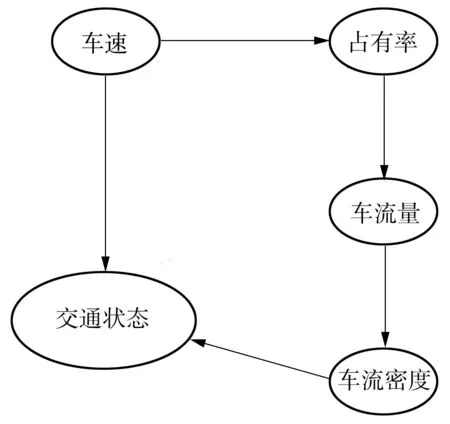
图1 判别交通状态的贝叶斯网络

(3)贝叶斯网络的演变和发展

除了传统的贝叶斯网络以外，一些非传统的贝叶斯网络也开始涌现。在一般情况下，交通流对时间敏感，具有明显的高峰时段，因而在目前的研究中，常常使用含有时间序列的贝叶斯网络来提高预测准确度。张敬磊等[53]建立了基于时间序列的动态贝叶斯网络，为贝叶斯网络增加了时间维度。

此外，由于单一模型的适用范围小、普适性差，贝叶斯网络通常与其它基本预测模型结合组成贝叶斯组合模型，通过贝叶斯网络的后验概率计算得到各个基本模型的权重，从而实现对交通流的联合预测，提高模型的普适性。如王建[54]等利用贝叶斯网络实现了多方案组合的交通流短时预测，首先建立基于小波分析的BP神经网络算法、ARIMA算法等基本模型对交通流进行预测，然后将基本模型的预测结果和实际结果离散化处理后，利用贝叶斯网络推理获得在各个基本模型的预测结果组合下的联合预测结果的概率分布，使得贝叶斯网络成为多方法组合预测交通状态的有效载体。

2.1.2 马尔科夫模型在预测交通状态方面的应用

(1)马尔科夫过程

马尔科夫过程是一类随机过程，它的特点在于未来的变化趋势仅取决于现在的状态，而与过去的演变无关。Yu等[55]利用马尔科夫过程的特性建立模型，对校园道路拥堵的预测进行了研究。

(2)马尔科夫链

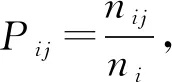
郑建湖等[56- 57]，结合大量的交通状态转移数据，利用马尔科夫链完成了对交通状态的预测。李军怀等[58]将马尔科夫链与指数平滑法相结合，兼顾了历史数据的演变和当前状态对未来变化趋势的影响，进行交通状态的预测。

(3)隐式马尔科夫模型

隐式马尔科夫模型较于传统的马尔科夫模型多了一个隐含的状态链，即存在两个随机次过程。Zhu等[59]利用隐式马尔科夫模型，不仅考虑特定道路区域本身的交通流状态变化，还考虑到特定道路区域的交通流状态变化与其它道路区域交通状态的关系。这对于一个路网的交通拥堵预测具有重要的意义。

2.2 非参数统计方法判别交通拥堵

与参数统计方法相比，非参数统计方法对数据和模型的假定更少，适用范围更广，结果也更加稳定，因此也更加适用于复杂的交通系统。

2.2.1 支持向量机模型(SVM)

传统的统计模式判别方法在样本量较大的情况下进行研究，而支持向量机[60]却能够很好的解决小样本问题，在统计资料较少的交通问题研究中具有良好的表现。它在20世纪90年代中期被提出，是一种有监督的统计机器学习方法。最初的SVM理论只能用来解决二类分类问题，随着各国学者的不断研究，多分类SVM算法以及与其他数据挖掘方法相结合的理论逐步建立并完善，支持向量机的应用也更加广泛，并被用于交通拥堵的模式判别。

SVM理论的核心思想是将输入向量非线性地映射到一个高维度特征空间中，之后在这个空间中构建一个决策超平面，将空间里的多个向量根据设定好的不同特征分为两大类。每个分类中距离分隔平面最近的向量是该分类的边缘向量，即支持向量。当两个分类的支持向量与平面的距离相等且取到最大时，认为该平面是最优的决策超平面，距离和也称为最优间隔。图2是一个二维空间下的例子，灰色部分选中的为支持向量，中间的虚线为最优超平面，两端实线间的距离即最优间隔。

图2 二维支持向量实例[57]

SVM算法在应用时的两大难点为超参数的选择和核函数的确定，针对前者，Hong等[61- 62]将SVM模型结合模拟退火算法(SA)和蚁群优化算法(ACO)进行解决，较好地预测了交通流状态，为拥堵判别提供了基础。而在针对核函数进行的研究中，Wang等[63]采用小波函数构造了一个新的核函数，Cong 等[64]则将果蝇优化算法(FOA)和最小二乘支持向量机模型(LSSVM)结合起来，取得了较为理想的结果。

支持向量机有着小样本、高泛化的优点，在交通状态的划分及交通拥堵的判别上有着较好的应用，关键在于与其他数据挖掘方法或优化算法的结合，来提高分类的精度，增大判别交通拥堵的准确性。

2.2.2 K-邻近算法(KNN)

KNN是非参数统计算法中一种较为简单的数据挖掘方法，其思路是：某个待测的数据在特征空间中有k个距离最近的已知类别的数据，那么这k个数据中的大多数属于哪一类，该待测数据也属于这一类[65]。

原始的KNN模型仅采用时间序列作为计算标准，而Cai等[66]改进了KNN模型，用时空状态矩阵描述路段的交通状态，更适于短期的交通状态预测。Xu等[67]先提取比较具有代表性的交通流数据建立了道路交通状态的参考序列，之后提取区域交通的吸引子序列构造核函数，得到当前序列与参考序列的距离，最后获得k个最小的距离，即利用核KNN算法(Kernel-KNN)判别了当前序列的所属交通状态。

KNN算法通过多对象中的占优类别进行决策，而非单一决策，因此能更好地进行交通拥堵状态判别。其对于样本的要求高于SVM模型，但在实际应用中，相较于支持向量机的非线性映射与构建线性决策超平面，KNN算法又更加易于处理。与决策树模型相比，KNN算法同样易于理解和使用。

2.2.3 神经网络

神经网络(ANN)是近40年来人工智能领域的研究热点。它作为典型的监督机器学习算法，已被广泛用于交通状态判别。目前应用于交通拥堵判别预测领域的神经网络模型有：BP神经网络、递归神经网络、多层反馈神经网络、径向基RBF神经网络等。

最基础的ANN架构包括输入层、输出层和隐含层。含有多个隐含层的感知器即为深度学习结构。如图3所示。

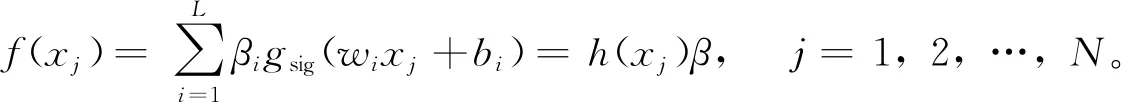
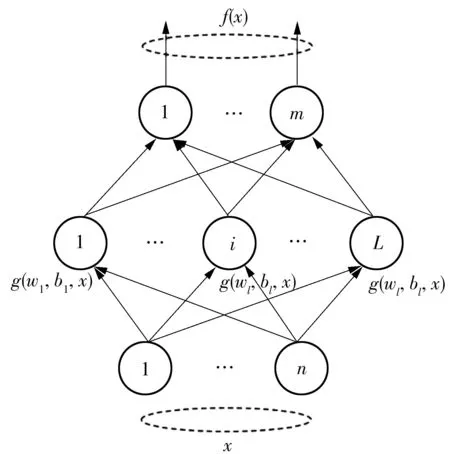
图3 最基础的ANN架构

式中,wi=[wi1,wi2,…,win]T是输入和第i个隐含层节点的连接权重。而βi=[βi1,βi2,…,βim]T是第i个隐含层节点和输出的权重。bi是第i个隐含层节点的偏置。

(1)BP神经网络

实际的交通系统是实时变化的，十分复杂，因此对于交通状态的判别模型需要能反映动态变化。Smith等[68]在BP神经网络模型与基于历史数据的算法和时间序列模型等较传统方法的比较中，发现BP模型在结果的准确率上相对较优，更能反映动态条件，并且没有时间序列模型的滞后和过度预测特征；BP算法是神经网络中最具代表性的网络训练方法，它通过梯度下降法求得隐含层节点参数的最优取值[69]。

虽然BP算法检测精度高，但是它学习速度较慢；因为是梯度下降，可能得到局部最优收敛而非全局最优收敛，从而导致网络训练失败。

(2)递归神经网络

时间序列交通流量预测要求模型的输入为序列数据，而递归神经网络(RNN)模型可以用来处理序列数据。递归神经网络记忆历史数据的输出，并且随着网络的外部输入作为下一时刻隐藏层单元的输入，该属性使网络可以动态记忆[70- 73]。

Ulbricht[74]介绍了解决短期交通预测任务的递归神经网络。在使用面向对象的神经网络进行短期交通状态预测的研究中，Dia等[75]发现5 min速度预测的延时递归神经网络(TLRN)非常准确，精度达到90%～94%。

(3)多层神经网络

多层感知器包括至少一个隐藏层，可以判别线性函数，也可以判别非线性函数，对于非线性的交通参数预测具有非常好的效果。例如，Chen[76]介绍了多层前向神经网络在回路检测站预测高速公路交通状况的设计。结果表明，神经网络在低、中、高容量条件下(包括反复出现的拥塞和可能发生的事件期间)在体积、占用率和速度预测方面具有高精度；2005年，Vlahogianni等[77]提供了一种基于高级遗传算法的多层感知神经网络交通流量预测模型，该模型不仅可以协助交通流数据的正确表示，也可协助时间、空间特征和神经网络结构的选择。

(4)径向基神经网络RBF

RBF神经网络有全局近似与收敛的特性，所以使得它成为交通流判别预测的主要选择之一。RBF神经网络的隐藏层空间是由径向基函数作为隐单元的“基”构成，隐节点被高斯函数定义：

(6)

式中，ci是第i个RBF隐藏集合的中心，xi是第i个RBF隐藏集合的宽度。

隐含层将低维的输入矢量映射到高维特征空间。在该较高维空间中绘制最佳分离超平面，以将点分成不同的组，同时最大化线性决策边界之间的边界。其网络结构简单，训练简单，学习收敛速度快，具有接近任何非线性函数的能力，可以处理复杂的交通系统的拥堵判别问题。Park等[78]比较了4种神经网络模型，如径向基神经网络(RBF)等，得出以下结论：RBF神经网络模型效果最好，比BP神经网络需要更少的计算时间。虽然RBF神经网络优于指数平滑法，但它比指数平滑法更复杂。

以上提及神经网络在交通状态判别与预测问题上表现优异，但神经网络用于交通流预测也存在着一定的局限性。如训练需要大量数据，若数据量过大则训练太耗时，若数据量过小则结果不够精确。另外，隐层节点的数量需要由经验进行确定，太多将导致计算时间过长，太少又难以达到实际问题中计算精度的要求。

2.2.4 聚类

聚类是常见的无监督的机器学习算法之一，可以在没有任何先验知识的情况下对交通流量数据进行分类。聚类旨在最小化类别内的差异并使各个类别的差异最大化。

K-means聚类是最常见的聚类之一，2011 年，Montazeri等[79]提出了一种基于行驶路段聚类的交通状况判别方法。使用k均值聚类算法判别驾驶特征并将其用于行驶路段聚类。结果表明，使用所提出的方法可以正确判别87%的交通状况；2010 年，Azimi等[80]采用3种模式判别方法对高速公路交通流状况进行流动特征分类。方法有K-means，Fuzzy C-means和CLARA(聚类大应用)。确定了与HCM分类一致的最佳聚类方法：K-means聚类。然后使用聚类方法补充HCM交通流状况分类。此外，这些方法提供了合理分类过饱和流动条件的手段；但K-means聚类对聚类数目和噪声数据的初始化很敏感，系统聚类缺乏鲁棒性，非唯一性且难以解释，所以此算法不能通用。

因此出现了嵌套和SOM等聚类。嵌套聚类类别数由数据的统计特性来确定，不断分组直到差异过小不能分组为止。如2007 年，Xia 等[81]介绍了一种嵌套聚类技术及其在高速公路运行状况分析中的应用：利用探测器收集的交通数据(流量、速度、占有率)开发了一个聚类模型，并以5 min为增量进行聚合。

自组织映射(SOM)神经网络聚类是一种竞争学习型的神经网络，它能将高维输入数据映射到低维空间，同时保持其拓扑结构不变，即将高维空间中相似的样本点映射到输出层相邻的神经元。它易于解释和可视化，所以SOM在分析具有时变性和充满噪音性质的交通流数据方面具有优势。Andrienko等[82- 83]已经在具有真实城市交通数据的大型数据集上得到验证，SOM能够对拥堵及其时空演变规律进行有效判别。

通过分析交通状态判别方法的研究现状可以发现，因现实中缺乏各种属性参数和标签的数据，聚类分析已成为判别交通拥堵的最重要方法。但是，聚类方法从大数据中提取特征通常需要花费大量时间，所以可能无法满足交通拥堵判别的实时性。于是，Chen等[84]提出了一种新的聚类算法，实时自动监测和分析交通状况。以道路上的车辆为数据点，提出了一种基于人工免疫网络的K-means网格密度聚类算法，将车辆数据划分为适当的簇，并标记密度，以监测和分析交通状况。仿真实验结果表明，该算法比传统方法具有更高的效率和稳定性。

表4 机器学习模型与应用

机器学习模型使用数据驱动方法，能够克服数学和物理模型描述复杂交通流的局限性，它们没有固定结构约束，被证明与数据有更好的拟合。从概率图模型到支持向量机、K-近邻算法、神经网络和聚类，这些机器学习方法，对于拥堵产生的异常特征及其特征变化十分敏感，能够大幅提高拥堵判别的可靠性。

3 结语

交通拥堵是诸多交通问题中影响最大、持续时间最长、出现频率最高的问题。如想解决此问题，最先要做的就是能够判别交通拥堵，然后利用各种信息平台诱导车辆合理选择行车路线。因此本文涵盖传统交通流理论与机器学习两大类方法，系统综述了国内外拥堵判别的方法。总体上，文献的特点包括以下3点：

(1)国外学者对于交通拥堵现象的系统研究起步较早，已经进行了许多较为有力的探索。国内学者在交通拥堵判别方面的研究虽然起步较晚，但根据我国的实际情况进行了很多创新与拓展。

(2)传统交通流理论与机器学习两大类方法并不是完全分开的，只是它们所针对的应用场景和采取的研究手段有所区别。传统交通流理论物理意义明确但严谨、限制条件苛刻，机器学习方法注重实际应用，但理解起来更困难。在研究不同的问题时它们各有优缺点。

(3)不可否认，使用机器学习方法来判别交通拥堵的趋势愈加明显。机器学习算法可以有效地分析利用数据，一些机器学习方法能够更好的检测交通异常事件，并更好地识别车速的降低、道路占有率的增加以及拥堵车流的出现等特征，许多研究都证明机器学习的算法有着强大的能力和可靠性，算法本身也在不断创新。并且，随着数据处理相关设备的更新，科研工作者数据处理能力的提高与信息科技的进步，交通领域积累了大量的数据，这也给机器学习算法提供了广阔的应用空间。

国内外学者在交通拥堵判别方面已经获得了较为丰富的成果，并逐步建立了相对完整的理论体系。然而已有研究还存在以下几点不足：

(1)缺乏对交通拥堵的统一定义和衡量标准

判别拥堵时研究者们往往给参数设定某一阈值，当达到这一阈值时，就可以判定交通拥堵状态的形成。因为没有统一定义和衡量标准，不同地区阈值不一样，因此各标准不具有普适性，大大增加了判别拥堵的工作量。

(2)缺少传统交通流理论与机器学习方法的协同合作

机器学习方法作为交通拥堵判别的重要组成部分，随着数据相关设备的更新，数据处理能力的提高与信息科技的进步，应用前景将更加广阔。而传统交通流理论作为交通领域的宝贵财富，曾指导许多交通拥堵判别问题，但目前两者的协同合作并不密切或深入。因此，为更好地完成交通拥堵判别，需要加强传统交通流理论与机器学习方法协同使用，进一步完善交通拥堵判别理论。

(3)应用于拥堵判别的参数不足

首先，数据获取困难，尤其是对于有高样本量要求的参数统计方法，取得符合训练要求的数据不太容易。另外，交通流参数众多，但现有研究中，每种方法只能关注几个参数，通过选取的部分参数进行交通流状态判断，并进而判别拥堵情况，这可能会导致解释出的结果存在一定片面性。

总体而言，无论是传统的交通流理论方法，还是新兴的机器学习的方法，在进行交通拥堵状态判别时，往往都会以流量、密度、速度、占用率、车头时距等交通流参数为基础进行交通状态判断，进而再检测拥堵。这些方法使用类似数据的区别在于：传统的基于指标的判别方法借助各类设备或信息平台直接监测路网内的相关数据，通过与阈值的比较来判断是否拥堵。而传统方法中的元胞传输模型与元胞自动机模型由于数学理论较强，大多通过纯数学方法处理数据、进行研究。机器学习方法则看重数据特征的挖掘和样本的训练，因此，即使采用的数据类似，处理方法也完全不同。考虑到已有研究的不足，未来的研究可基于(但不限于)以下几个研究方向：

(1)考虑各国对拥堵的不同定义与衡量标准，基于高速发展的信息搜取和整合技术，收集整理实际常使用的拥堵衡量标准，进而建立简单通用的拥堵衡量标准，完善拥堵判别的理论研究体系；

(2)针对难以理解的机器学习模型，在已知输入输出的情况下，采用其他方法如敏感性分析等反推变量内部联系。这样既可以保证判别预测的精确度，又可以帮助理解变量的影响；

(3)考虑传统交通流理论与机器学习方法协同合作。利用机器学习中优秀的算法及解决问题的思路来优化传统交通流模型，小到可以考虑对排队论、流体力学模型、动力学模型等模型的某一步骤进行改进，大到利用算法减少人为对交通流规律分析、交通问题机理诊断判别的步骤。两者互相配合，以期更好地判别交通拥堵。

(4)在未来，在研究数据这一方面还可以展开如下工作：首先，建立各省市完善统一的交通信息平台，形成完整的交通流参数数据库，便于各项拥堵判别的研究；其次，鉴于某些模型需采用特定参数，为了更好的利用其它参数数据，可以更多发掘不同参数之间的关联，以获得方便可行、解释全面、更具说服力的结果。