褶皱山区NDVI与地形因子的多尺度耦合关系研究
2021-05-13王慧玲熊亚兰陈小凤
王慧玲,熊亚兰,陈小凤,刘 颖
(四川农业大学资源学院,成都 611130)
归一化植被指数,即NDVI(normalized difference vegetation index)数值,其动态主要受地形特征和人为因素的影响[1]。NDVI可以削弱大气层和地形阴影的影响,对地表植被的覆盖程度非常敏感,是目前检测和指示植被覆盖状况和动态的常用指标之一[1]。在山区,地形因素显得尤为重要。其通过影响太阳辐射与降水的空间再分配过程,对植被分布格局的塑造起着不可或缺的作用[2]。利用地形差异来揭示植被空间分异规律,是自然地理、生态学等领域的重点研究方向之一。如仇宽彪等研究了基于NDVI太湖流域片植被覆盖变化[3]。邓元杰等研究了长江流域中上游植被NDVI时空变化及其地形分异效应[4]。刘梁美子等研究了黔桂喀斯特山区NDVI与地形之间存在的相关性[5]。而三峡库区重庆段的渝东北地区是长江流域重要生态屏障和长江上游特色经济走廊[6],但该区域内褶皱山脉广布、山高坡陡、土层浅薄,农业生产较为落后,因此生态环境保护任务重,发展农业生产的压力大,有必要对该区植被覆盖情况与地形因子的关系进行全面深入和多尺度的研究。
地形要素作用于一系列的地理过程,从而对区域植被的格局产生影响,而简单的相关性分析不足以揭示这其中的影响关系。目前对于植被覆盖指数和地形因素的相关影响程度伴随着小波变换分析法的发展,已由静态、单一尺度转向动态、多尺度划分[7-8]。小波分析被称为“数学显微镜”,可以揭示自然或生态因子的多尺度格局,并且不要求数据符合二阶平稳假设[9-11]。过去对NDVI与地形因子多尺度关系的研究主要是采样一维小波变换方法对研究区多条样带上NDVI与地形因子的多尺度相关性或小波相干性进行研究[12-15]。如李双成等通过小波变换揭示了西藏高原生态系统的NDVI与地形因子的多尺度空间格局和相关性[14-15]。李小梅等利用小波多尺度分析工具分析了福州市NDVI和地形因子等生态环境参数的尺度—格局特征以及生态环境参数相关关系的尺度响应[9]。邱炳文、邹伟成等利用离散小波变换对武夷山自然保护区的NDVI与地形因子进行了多尺度空间相关分析[16-17]。
样带的选择是一维小波变换研究中的关键,而克服样带代表性等的限制则需要运用到二维小波变换的方法。二维小波变换能将栅格数据进一步分解为低频和高频部分,高频部分又可划分为水平、垂直和对角3个部分。低频系数为实测值经过多尺度分解后的近似信息,可显示出实测值通过小波变换剩余的基本轮廓信息,若进一步分解,即分解尺度扩大。其更能滤去细节信息,趋向清晰化和简单化,从而较为直观地反映出研究对象的总体变化规律[9-11]。高频系数即实测值经过多尺度分解后的细节信息,反映出该变量在不同空间位置的波动变化情况,某个区域的波动变化越大,则反映了该区域研究对象变化越复杂,受到其他因素干扰的强度越大。故二维小波变换较一维小波变换更能从多方位、多角度、深入贴合地反映出植被与地形因子在大空间和小空间的耦合关系。因此本研究拟采用二维小波变换对褶皱山区NDVI与地形因子的多尺度耦合关系进行研究,研究结果在一定程度上能够为山区植被保护、生态环境恢复、水土流失治理和提高农业生产规划提供相关数据支撑。
1 材料和方法
1.1 研究区概况
研究区(108°12′13″~108°54′27″E,30°48′33″~31°10′43″N)位于长江上游,川东平行岭谷东北部,面积约2 700 km2(图1)。该区域属亚热带季风气候,立体气候显著,四季分明,光照充足,雨量丰沛,降雨量1 200 mm左右,年平均气温18℃左右。全区为两列褶皱山脉由北东—南西走向转为西东走向的转折地带,地势西高东低,海拔高度为78~1 350 m;出露地层的地质年代多见于中生代三叠纪和侏罗纪,侏罗纪地层分布最广,三叠纪次之;山地和丘陵广布;土壤类型以黄壤、紫色土、石灰土和水稻土等为主[18]。海拔500 m以下的丘陵区主要为农耕区,海拔500~1 350 m的低山和中山下部,自然林被主要为常绿阔叶与落叶阔叶混交林[2]。

图1 NDVI和地形因子的多尺度空间分布图Figure 1 Multi-scale spatial patterns of NDVI and topographic factors

图1 研究区位图Figure 1 The location of study area
1.2 研究方法
1.2.1 数据来源与预处理
研究区年降雨充沛,植被整体覆盖情况较好,在7月份和8月份植被覆盖度达到最大值,但其空间分布的差异较小,因此为了更好地反映地形对植被覆盖度的影响,本研究选择的是一年中植被覆盖度最低、空间差异最大的1月份(2016年)的植被覆盖度数据。MODIS合成的标准NDVI产品MODND1M为月内每天最大值,空间分辨率为500 m,坐标系为WGS84。
在山地生态学研究中,高程、坡度和坡向是地形的3个主要属性,也是决定植被生境其他要素分异(如土壤、小气候、水文等)的主导因子。本研究利用数字高程模型(digital elevation model,DEM)来计算并用ArcGIS提取得到高程、坡度和坡向。数据空间分辨率为30 m,坐标系为WGS84。
NDVI和DEM数据均在地理空间数据云平台下载,并在ArcGIS中将DEM重采样为500 m。考虑到研究区地形以山地和丘陵为主,且重采样前后空间分辨率差异较大,因此采用三次卷积插值法重采样。
1.2.2 小波多尺度分析的基本原理
设任意一个采样点坐标为(x,y),点坐标(x,y)变化时各要素的变化就形成了一个离散变化的二维信号(函数)f(x,y)。小波变换就是利用母小波(mother wavelet)与原函数内积,从而达到分解原函数的目的。二维小波变换的公式如下[19]:
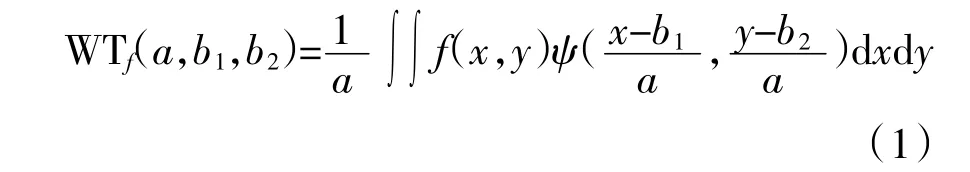
式中,WTf为小波系数,a为尺度因子,b1和b2分别为x和y方向的平移因子,ψ(x)为母小波,f(x,y)为待分析函数(网格实测值)。将母小波与待分析函数内积后,可得到不同尺度下的小波系数并对它们进行分解。本研究选取小波分析中常用的db6算法作为小波母函数,采用Mallat塔式算法。根据塔式算法,实测值与分解后小波系数的关系为[20-22]:

式中,j为分解的级数;A为低频系数;H、V和D分别为水平、垂直和对角方向的高频系数;G为多级分解尺度下3个方向高频系数之和。在MATLAB中完成了小波低频系数和高频系数的提取。
根据小波变换的原理,最大分解尺度与栅格行(列)的数量密切相关,若行(列)的数量为2n,那最佳分解尺度为n-2[11]。本研究采样点为128行、64列,因此可对NDVI和地形因子进行四级分解,分解后每一级所对应的网格大小分别为1 km×1 km、2 km×2 km、4 km×4 km和8 km×8 km。每一级小波分解后低频系数和高频系数对应的空间尺度单元(样点间距)会放大为上一级的2倍,即每级小波系数的个数会减少为上一级的1/2。通过二维小波重构可以确保不同分解尺度下小波系数的个数一致。小波分解后的小波系数是没有量纲的,但重构后的小波系数是有量纲的。
2 结果与分析
2.1 NDVI与地形因子的基本统计特征分析
小波低频系数反应全局变化态势,高频系数表征出细节信息,由于本研究中栅格尺度较大,因此只对低频系数进行分析。NDVI和地形因子的基本统计特征见表1。0.5 km尺度,NDVI的取值为0.09~1.00,均值为0.50,变异系数为24%,说明研究区植被覆盖情况良好,但具有中等程度的变异。高程、坡度和坡向的变异系数分别为49%、53%和58%,均为中等程度的变异。从0.5~8 km尺度,各要素最大值与最小值的距离缩小,变异系数、峰度和偏度均逐渐降低,但均值保持不变,这表明在小波分解的过程中随着尺度的增大,各要素低频信息得到平滑。

表1 NDVI及地形因子的基本统计特征Table 1 Basic statistical characteristics of NDVI and terrain factors
2.2 NDVI与地形因子的多尺度空间分布特征
基于小波低频系数的NDVI与地形因子空间分布见图2。根据国家《土壤侵蚀分级标准》[23]中的植被覆盖度分级标准,并结合研究区的实际植被覆盖情况,将植被覆盖度划分5个等级:<0.1(裸地)、0.10~0.35(低植被覆盖)、0.36~0.45(中低植被覆盖)、0.46~0.60(中等植被覆盖)、>0.6(高植被覆盖)。
从0.5~8 km尺度,随着分解尺度的增大,小波变换方法的平滑效应逐步强化,轮廓信息凸显出来而内部细节信息逐渐被弱化,使得NDVI空间分布规律更加简单明了。NDVI>0.6的区域主要为两列北东-南西走向的条带状区域,边缘呈齿状分布。利用多尺度分解后的NDVI空间分布图和高清遥感影像进行参照比较分析,可得知,该区植被主要为常绿阔叶与针阔叶混交林,NDVI>0.6的区域与平行岭谷的分布和走向极为吻合,齿状边缘主要是受山脉两侧岭谷相间的地貌特征影响。另外,NDVI>0.6的区域在长江两岸也有局部分布,这些区域的海拔在500米以下。NDVI为0.10~0.35的区域主要集中在平行岭谷两侧的丘陵地带,地表植被稀少,多为农耕区。NDVI<0.1的区域为裸地,裸地主要分布在农田附近。
综合5个尺度看,在高程、坡度和坡向3个地形因子中,高程和NDVI的空间分布格局最为相似,坡度和坡向与NDVI的空间分布相似度较低。坡度和坡向的多尺度空间变化特征不如NDVI和高程明显,但仍可识别出其在0.5~4 km尺度上呈北东-南西走向。
2.3 NDVI与地形因子的多尺度小波相关分析
多尺度相关分析可以更好地区分不同要素,将其耦合程度与单一尺度相关分析的耦合程度比较,显得更加合理。基于小波低频系数的NDVI与地形因子的相关性见表2。地形因子与NDVI相关性的大小的顺序为高程>坡度>坡向,并随小波分解尺度的增加而增大。从0.5~8 km尺度,NDVI与高程均呈极显著正相关,相关性随分解尺度的增加而增大,由0.256逐渐增加到0.507。主要原因在于该区域受海拔影响,在较低处地形为丘陵和平坝,受人类活动影响程度大,农业生产率高,伴随着海拔的增加,人类活动逐渐减少,植被生长茂盛。同时,由于研究区地形起伏空间尺度较大,因此随着空间尺度的增加,高程对NDVI的影响作用越来越明显。坡度与NDVI在各尺度下均呈正相关,相关性随分解尺度的增加而增大。呈正相关的原因在于该区坡度小的区域往往开垦为农田,坡度大于25°的区域受国家退耕还林工程影响植被覆盖较高。坡向与NDVI在5个尺度上均无相关性,其原因是该区山脉呈北东-南西走向,因此受太阳辐射影响的差异较小。同时,本研究中坡向的最小空间分辨率为0.5 km,而坡向是在较小尺度上对NDVI产生影响的因子,因此在较大尺度上对NDVI的影响不明显。

表2 不同尺度下NDVI及地形因子的相关系数Table 2 Correlation coefficients between NDVI and topographic factors at multi-scale
首先,本文构建了基于小波低频系数的NDVI回归方程(表3)。是为了更好地分析整理NDVI与地形因子,这两者之间的定量关系。本研究又在SPSS软件中采用逐步回归法对NDVI进行拟合,解决了建模因子共线性的问题。在0.5、1和2 km尺度,最优拟合方程的建模因子仅有高程,说明在该尺度范围虽然坡度与NDVI也有一定的相关性,但NDVI的高低主要由高程决定。在4 km和8 km尺度,拟合方程的建模因子为高程和坡度,说明在较大尺度上NDVI高低受控于高程和坡度。
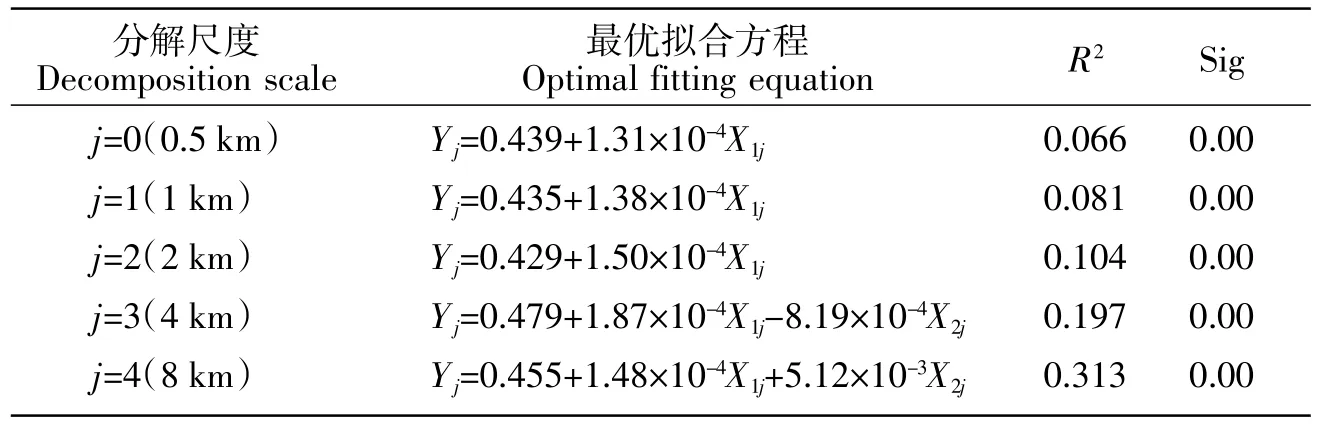
表3 不同尺度下NDVI的拟合方程Table 3 Regression prediction model and R2for NDVI at multi-scale
由回归方程的决定系数分析可知,伴随分解尺度的增加,拟合方程的R2由0.066提高到0.313,说明伴随分解尺度的增加,图片中微小的信息被过滤,小波低频系数反映的空间总体规律趋于清晰,NDVI和地形因子的关系更加明显。
3 结论与讨论
本文选择二维小波变换的实验方法,对褶皱山区NDVI与地形因子之间的多尺度空间耦合性进行分析研究,研究结果如下:①多尺度下NDVI和高程的空间分布相似度最高,高植被覆盖(NDVI>0.6)区域主要集中于褶皱山脉和长江两岸,低植被覆盖区域(NDVI<0.35)主要集中于丘陵农地。②综合5个尺度看,NDVI与地形因子相关性的大小的顺序为高程>坡度>坡向,其中,NDVI与高程和坡度的值都呈正相关,与坡向几乎无相关性,且相关性随小波分解尺度的增加而增大。③在0.5、1和2 km尺度,NDVI的最佳拟合方程中建模因子仅需高程,而在4 km和8 km尺度,最佳拟合方程的建模因子为高程和坡度,拟合方程的决定系数随着分解尺度的增加而增加。
高程、坡度与NDVI的相关性较高,且随空间尺度的增加而增大,说明两者倾向于在宏观尺度上影响NDVI的空间分布,这与胡云锋等[8,14-16]在蒙古高原、青藏高原、浙江省和武夷山的研究结果一致。NDVI回归方程的决定系数在5个尺度下均偏低,其原因在于NDVI与地形因子并非简单的线性关系,并且一些重要的影响因素如土地利用类型、距河流的距离等没有考虑,在今后的研究中可以尝试增加这些因子。
小波变换能够反映出NDVI和地形因子的多尺度特征,对于小波变换的方法来说仍然要考虑以下几个问题,首先因为本研究中所采用的MODIS影像的空间分辨率为0.5 km,所以不宜对小波分解后的细节信息进行分析,今后的研究中可以考虑采用分辨率较高的数据源,以便对NDVI和地形因子小波分解后的多尺度细节信息进行研究,以进一步揭示两者的多尺度耦合关系;其次,数学领域的研究已经表明,选择不同的小波基函数,会导致小波分解后结果发生变化[7,20],在研究中仍需进一步寻找有关小波基的筛分方法;最后,目前所采用的小波分析方法仅能给出断续尺度(即尺度必须为2n)上的小波系数,无法在连续尺度上开展计算和分析,此问题在今后的研究过程中仍需得到进一步解决[8,24]。
