比例时滞脉冲细胞神经网络的指数稳定性

龚爱爱,许友军,刘柏林

(南华大学 数理学院,湖南 衡阳 421001)

0 引 言

近些年来，脉冲微分方程的研究受到了许多学者和专家的关注[1-3]，同时，在许多领域中，如控制技术、药物管理和生物学等的阀值中出现了具有时滞脉冲细胞神经网络的稳定性[4-6]。文献[7]研究了比例时滞混沌神经网络的脉冲控制全局功率率同步问题。文献[8]应用了Lyapunov法和线性矩阵不等式(LMI)方法得时滞脉冲细胞神经网络平衡点渐进稳定的条件。文献[9]通过非线性变换和非线性测度方法分析比例时滞CNNs。文献[10]利用Lyapunov 函数和Razumikhin 技巧分析了泛函微分方程解的指数稳定性。

本文通过构造合适的Lyapunov 函数和Razumikhin 技巧研究了系统的全局指数稳定性，并获得了该系统平衡点全局指数稳定性的一个时滞依赖的充分条件。

1 模型描述和预备知识

研究如下比例时滞脉冲神经网络：

(1)

在系统(1)中，假设满足下列条件：

A1：存在常数Li>0，使得|Fi(u)-Fi(v)|≤Li|u-v|，其中u,v∈R，i=1,2,…,n。

A2：系统(1)存在唯一的平衡点y*。

(2)

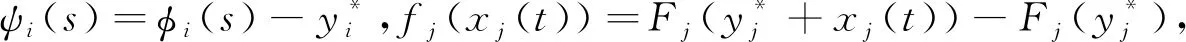
定义2 设函数V:[t0,∞)×Rn→R+，若V(t,x)满足:

(ii)在x∈Rn上，V(t,x)是局部Lipschitz的，对于任意的t≥t0满足V(t,0)≡0；则函数V∈v0。

定义3 设函数V∈v0，V的Dini导数定义为：

定义4 对于任意初始值xt0=ψ，存在常数λ≥0,M≥1，使得：

‖x(t,t0,ψ)‖≤M‖ψ‖e-λ(t-t0),t≥t0,

则称系统(2)的平凡解是指数稳定的。

2 稳定性分析

定理1 假设存在函数V∈v0，p、c1、c2、λ为大于0的常数，c2>c1，k=1,2,…,n。满足下列条件：

(i)c1‖x(t)‖≤V(t,x(t))≤c2‖x(t)‖;

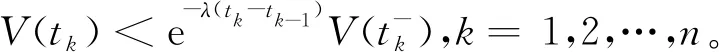
则系统(2)的平凡解是指数稳定的。

证明：设x(t)=x(t,t0,ψ)为系统(2)的解，V(t)=V(t,x)，下面要证明：

V(t)≤c2‖ψ‖e-λ(t-t0)，t∈[tk-1,tk)其中k=1,2,…,n。

当t∈[qt0,t0]时，由条件(i)得，

V(t)-c2‖ψ‖e-λ(t-t0)≤V(t)-c2‖ψ‖≤0。

建立Q(t)=V(t)-c2‖ψ‖e-λ(t-t0)，t∈[tk-1,tk)其中k=1,2,…,n,只需要证明当t≥t0时，Q(t)≤0。

当t∈[t0,t1)时，假设Q(t)≤0不成立，则存在t∈[t0,t1)使得Q(t)>0，又因为当t=t0时Q(t0)≤0，Q(t)连续，所以存在t*=inf{t∈[t0,t1]:Q(t)>0}使得Q(t*)=0,D+Q(t*)>0，故有Q(t)≤0,t∈[qt0,t*]，

当t=t*时，V(t)满足下列等式：

V(t*)=Q(t*)+c2‖ψ‖e-λ(t*-t0)；

所以当t=qt*时可得出：

由条件(ii)得，D+V(t*)≤-h(t*)V(t*) ，可得Q(t)在t=t*处的倒数：

与D+Q(t*)>0相矛盾，因此Q(t)≤0,t∈[t0,t1)。假设当t∈[t0,tm),m≥1时，Q(t)≤0，接下来证明当t∈[t0,tm+1),m≥1时，Q(t)≤0。

由条件(iii)可得出：

接下来证明当t∈(tm,tm+1)时，Q(t)≤0；假设该不等式不成立，由Q(tm)≤0和Q(t)的连续性可知存在t*=inf{t∈[tm,tm+1]:Q(t)>0}使得Q(t*)=0和Q(t)≤0,t∈[t0,t*]。

因为V(t*)=Q(t*)+c2‖ψ‖e-λ(t*-t0)，

即可得出：

由条件(ii)得，D+V(t*)≤-h(t*)V(t*)，则有：

与假设矛盾，因此Q(t)≤0，t∈(tm,tm+1)。由归纳法可知Q(t)≤0，t≥t0。

即得出：

V(t)≤c2‖ψ‖e-λ(t-t0)，t∈[tk-1,tk)其中k=1,2,…,n。

由条件(i)，得c1‖x‖≤V(t)≤c2‖ψ‖e-λ(t-t0)，所以有‖x‖≤M‖ψ‖e-λ(t-t0),t≥t0，其中M=(c1/c2)≥1，因此系统(2)的平凡解是指数稳定的，也就是说，系统(1)中的平衡点也是指数稳定的，收敛指数为λ。