基于轨迹灵敏度的暂态过电压两阶段优化控制

王长江 姜 涛 刘福锁 陈厚合 鲁华威

（1. 现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学） 吉林 132012 2. 智能电网保护和运行控制国家重点实验室南瑞集团（国网电力科学研究院）有限公司 南京 211106）

0 引言

近年来，以风电为代表的新能源发电技术得到快速发展[1-4]，大规模风电经高压直流（High Voltage Direct Currents, HVDC）远距离输送到负荷中心时[5-6]，若发生受端交流系统短路、直流闭锁、换相失败等功率大扰动，将打破直流送端系统的无功平衡，大量盈余无功涌入直流送端系统，易造成直流送端系统的暂态过电压，引发风机脱网及连锁反应[7]，严重威胁交直流混合系统的安全稳定运行[8-10]。因此，抑制直流送端系统暂态过电压对提高含大规模风电的交直流系统稳定性具有重要意义[11]。

目前，国内外对抑制直流送端系统暂态过电压的研究，主要集中在增设辅助装置和优化控制系统两方面[12-20]。在增设辅助装置方面，文献[12-14]分别通过配置动态无功补偿器、动态电压恢复器和调相机等辅助装置，能在一定程度上补偿故障与正常情况的电压差值，抑制暂态过电压，规避风机脱网，但会增加系统的投资。在优化控制系统方面，文献[15]基于时域仿真法，从优化直流系统整流侧电流控制环节和低压限流环节的控制参数来抑制暂态过电压，该方法计算精度高，能准确、直观地反映故障后系统的暂态过程，但计算速度较慢，优化过程相对繁琐；文献[16]提出一种孤岛附加控制策略来改善“风火打捆”特高压直流系统的频率和电压稳定性，可通过改变直流系统功率指令来灵活调节直流功率，进而改善特高压直流系统的稳定性；文献[17]在直流闭锁场景提出一种暂态过电压的极控（切滤波器）和安控（切机）动作时序协调控制方法，可有效避免“二次压升”的风险[18]；文献[19-20]分别提出了双馈风电机组的虚拟阻抗控制方法和直流系统的动态无功支撑控制方法来优化系统的控制性能，抑制暂态过电压，但增加了控制系统的复杂程度。上述研究从增设辅助装置和改进系统自身控制的角度出发，可较好地抑制暂态过电压，但暂态过电压的动态过程较快，易伴随风机连锁脱网等现象，而控制装置从接收控制指令到装置动作需要一定延时，很难确保在暂态过电压动态过程中予以实时抑制。因此需要在故障发生前采取适当的预防控制措施。预防控制可通过调整发电机的机端电压、变压器分接头位置、系统无功补偿设备以及网络参数等措施改变系统的当前运行点，使系统在发生暂态过电压失稳前将系统关键母线电压控制在合理范围，有利于避免暂态过电压失稳引起的大范围连锁性电压失稳或崩溃，提高区域系统整体的稳定性。该方法无需增设额外辅助装置或引入复杂控制环节，所需控制代价较低[21]。因此开展暂态过电压的预防控制措施研究，可在保证经济性的前提下，有效避免直流送端系统暂态过电压的出现。

国内外学者在电力系统暂态电压预防控制方面已进行了很多有益探索[22-26]。文献[22]通过调整发电机出力，使暂态过程中的关键母线电压轨迹运行在安全范围，但控制措施相对单一，且未考虑其他控制措施对暂态电压安全的影响；文献[23]通过稳态运行时的电压协调控制，可有效预防风电机组在扰动期间的连锁故障，提高风电场扰动时的安全性；文献[24]提出了一套考虑快速动态无功补偿装置的二级电压控制体系，可改善扰动后系统电压的恢复效果；文献[25]提出的暂态电压优化控制模型，通过调整并联电容器组和变压器电压比等控制量，确保暂态电压快速恢复稳定。由于暂态电压优化控制模型中包含电力系统的动态过程，需要求解复杂的非线性代数微分方程组，使优化模型的计算效率较低。文献[26]借助轨迹灵敏度法将暂态电压优化控制模型转换为线性规划模型，并采用启发式优化求解方法获得近似最优解，可有效降低优化控制模型的复杂度。虽然现有暂态电压预防控制可有效地改善暂态电压的安全性，但缺乏交直流送端系统暂态过电压的预防控制研究，且控制措施主要采用交流系统的传统控制元件，忽略了直流和风电等控制元件对暂态电压的影响。鉴于现有交直流送端系统暂态过电压预防控制研究匮乏和模型求解复杂的问题，将轨迹灵敏度方法应用到暂态过电压预防控制，降低暂态过电压优化控制模型的复杂度。采用直流送端系统暂态过电压和恢复阶段电压的两阶段优化控制，兼顾直流送端系统恢复过程电压不安全的风险，改善交直流送端系统的暂态过电压稳定性。

针对上述问题，本文提出一种基于轨迹灵敏度的暂态过电压两阶段优化控制方法。首先，分析含大规模风电的交直流送端系统暂态过电压产生原因，并介绍轨迹灵敏度和模型预测控制（Model Predictive Control, MPC）的基本原理，基于MPC 构建暂态过电压的两阶段控制模型，借助轨迹灵敏度将暂态过电压的非线性控制模型转换为二次规划模型。然后，针对直流送端系统暂态过电压失稳场景，在故障发生前求解暂态过电压预防控制的控制量变化值值，并将控制量变化值施加到交直流系统，避免严重的暂态过电压危害，若控制实施后恢复阶段电压不安全，同理将恢复阶段电压控制的控制量变化值施加到交直流系统的恢复过程，并滚动调节控制量直至暂态过电压恢复过程运行在安全范围内。最后，通过修改后IEEE 39 节点系统的仿真分析验证所提优化控制方法的有效性。

1 暂态过电压的产生原理

借助大规模风电经HVDC 外送的简化模型，分析直流送端系统暂态过电压的产生原理。直流送端系统换流站与风电场之间的无功功率交换示意图如图1 所示。

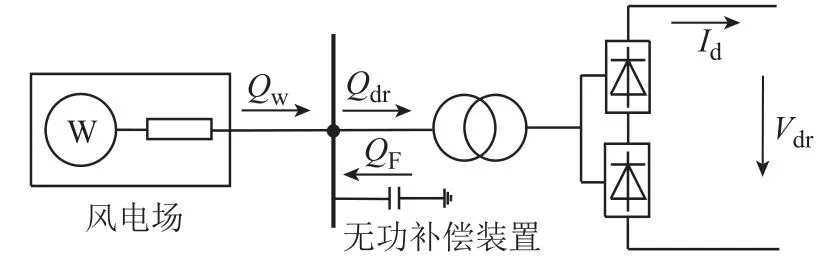
图1 换流站和风电场无功功率交换示意图Fig.1 Diagram of reactive power exchange between rectifier station and wind farm

图1 中，Qdr为换流站吸收的无功，Qw为风电场出口发出的无功，QF为滤波器发出的无功，Id为直流电流，Vdr为整流侧直流电压。整流站和风电场之间的无功平衡关系为

由式（1）可知，Qdr、Qw、QF只有满足上述无功关系，才能保证整流站与风电场间的无功平衡。当受端交流系统故障导致直流换相失败后[11]（整流侧动态过程包括直流侧短路、直流电流减小和恢复阶段），在直流电流减小阶段，直流电流因电流控制超调而低于目标值，甚至降为零，Qdr随之降低[27]。此时，为满足无功平衡需减小Qw和QF，而故障后的暂态过程中QF变化较小，近似为稳态值[15]；Qw受风电场与整流站间通信延迟的限制而无法及时减小[28]，使整流站与风电场之间的无功平衡被打破，导致直流送端产生大量盈余无功，造成直流送端系统的暂态过电压，可表示为

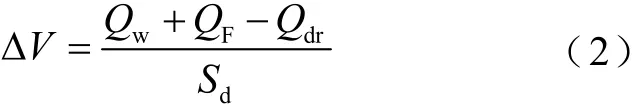
式中，ΔV为换流母线暂态电压变化率；Sd为系统短路容量。

由于直流送端系统暂态过电压发生在直流电流减小阶段，一般为故障切除后70～170ms[11]，很难在故障切除后及时施加暂态过电压控制，而且施加控制后有可能引起恢复阶段的电压不安全现象。因此，如何兼顾直流电流减小阶段的暂态过电压失稳和恢复阶段的电压不安全，仍是抑制直流送端系统暂态过电压急需解决的问题。

2 暂态过电压的两阶段优化控制

由于直流送端系统暂态过电压一般发生在故障切除后的几十毫秒，难以在动态过程中及时给予控制，故可在故障发生前求解暂态过电压预防控制模型获得控制量变化值，并施加控制到交直流系统，规避暂态过电压风险。由于施加预防控制后，有可能引起恢复阶段的电压不安全，需实时监控恢复阶段的电压安全性，若检测到恢复阶段电压不安全则求解恢复阶段电压控制模型获得控制量变化值。由于恢复阶段的电压属于长时间尺度问题，可实施MPC 控制来改善电压安全性，进而在抑制直流送端系统暂态过电压的同时，确保恢复阶段电压运行在安全范围内。同时借助直流送端系统暂态过电压和恢复阶段电压对控制量的轨迹灵敏度，将非线性控制模型转换成以控制量增量为独立优化变量的二次规划模型，改善模型求解效率。

2.1 交直流系统的轨迹灵敏度

交直流系统轨迹灵敏度可随时间不断变化，反映参数微小变化对交直流系统运行状态的影响[29-30]。电力系统动态过程可表示为

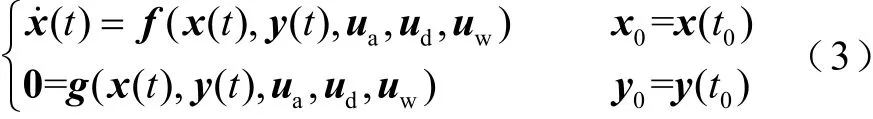
式中，x(t)和x˙(t) 分别为系统状态变量在时刻t的向量和导数；y(t)为代数变量在时刻t组成的向量；ua、ud和uw分别为交流系统、直流系统和风电场的控制量，u=[uauduw]；x0、y0分别为x(t)、y(t)在时刻t0的向量，本文采用Фx(u,t)、Фy(u,t)表示交直流系统状态变量和代数变量的变化轨迹，即

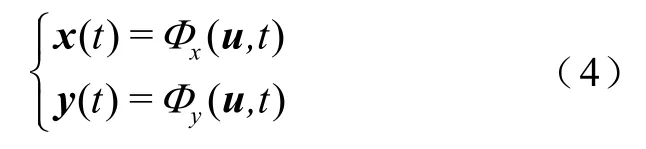
将x(t)和y(t)在u=u0处进行泰勒级数展开，并忽略控制量增量Δu的高阶项，由Δu引起时刻t的状态变量增量Δx(t)和代数变量增量Δy(t)可近似表示为

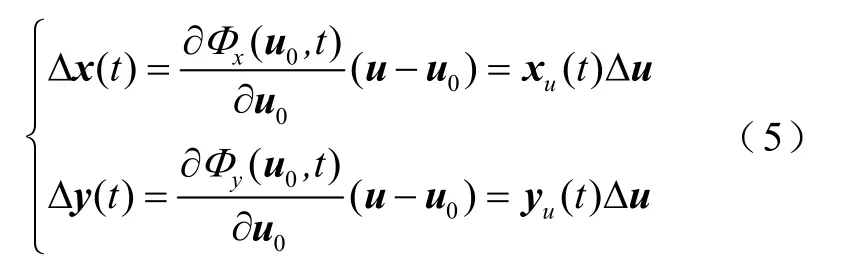
式中，xu(t)、yu(t)为x(t)、y(t)关于u的轨迹灵敏度。当Δu足够小时

由式（6）可知，当系统控制量变化Δu时，可利用轨迹灵敏度求得系统状态变量和代数变量的变化轨迹。轨迹灵敏度有解析法和摄动法两种求解方法。针对大规模交直流混合系统结构复杂和方程维数较高的特点，普遍采用摄动法求解轨迹灵敏度，该方法适用于复杂的黑箱系统，无需考虑系统的线性化和网络拓扑特点，便于得到轨迹灵敏度的近似值，避免了解析法繁琐的数值积分过程。

采用摄动法计算直流送端系统节点电压对控制量的轨迹灵敏度，可将控制量的变化区域划分为Z个离散时间点，第i个离散时间点的直流送端系统节点电压为Vi，i=1, 2, …,Z。采用式（7）的中心差分、正向差分和反向差分法（本文采用正向差分法）计算直流送端系统电压对控制量的轨迹灵敏度，并选取灵敏度值较大的控制量作为关键控制量。

2.2 模型预测控制的基本原理

直流送端系统动态过程中的直流电流减小（即暂态过电压）阶段时间尺度较短，可在故障发生前施加暂态过电压优化控制的控制量。然而直流送端系统动态过程中的电压恢复阶段时间尺度较长，可采用MPC 原理在线求解恢复阶段电压优化控制模型和在线实施控制决策，实质为不断滚动的局部优化和在线控制过程。MPC 原理如图2 所示，其中，y为被控量；u为控制量；Δu为控制量增量，Δuk+1和Δuk+m-1分别为k时刻预测到的第1 个和第m-1个控制量增量；yr(t)为参考轨迹；yp(t)为预测轨迹；y0(t)为未加控制的实际轨迹；c为被控量的目标值；Ts为采样周期；m为控制周期数，N为预测周期数，且m≤N；在预测时域[tk，tk+N]内求解优化问题，使控制后的yp(t)接近yr(t)，得到控制时域[tk,tk+m-1]内的各控制量。由于实际系统建模不精确以及干扰的存在，将t≥tk的所有控制量施加到系统中可能会进一步增加误差。因此在tk时刻仅实施控制动作序列的第1 个控制，重复上述过程以实现预测控制。

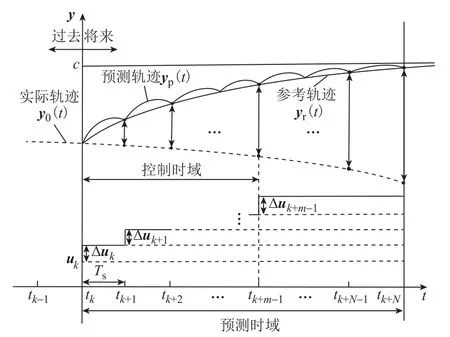
图2 MPC 原理Fig.2 Principle of MPC

现有非线性MPC 模型的目标函数综合考虑了各采样时刻预测轨迹与参考轨迹的偏差和各控制量的控制代价，控制模型为

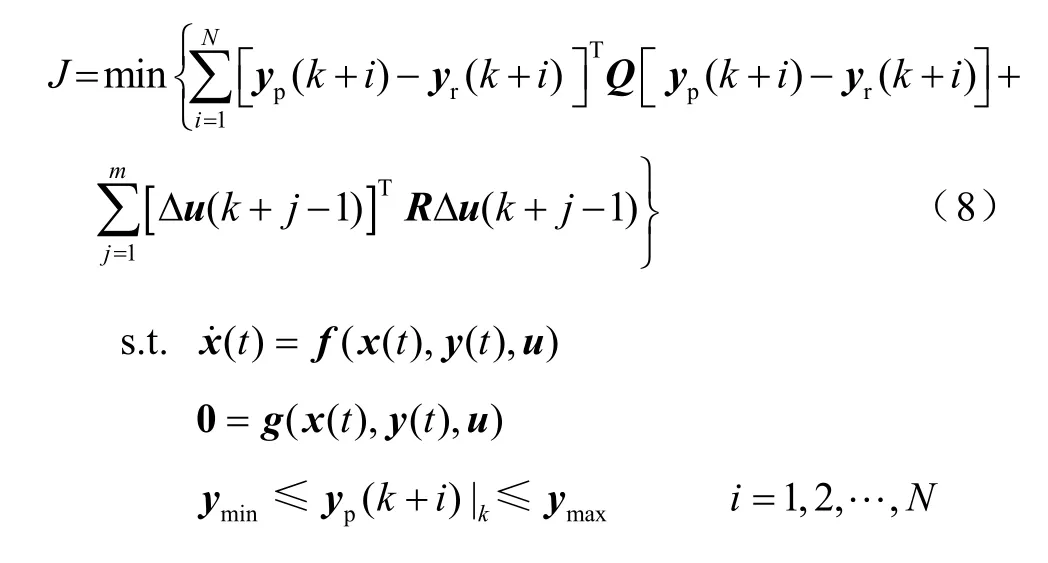
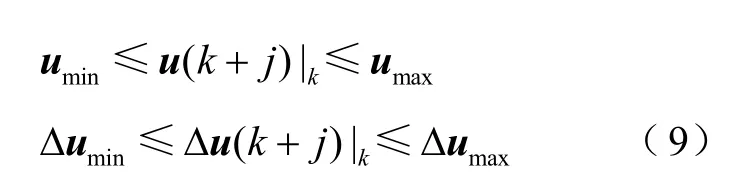
式中，Q和R分别为加权对角矩阵；ymax、ymin分别为被控量的上、下限；umax、umin分别为u的上、下限；Δumax、Δumin分别为Δu的上、下限；j=1,2,… ,m。

由式（8）和式（9）可知，传统非线性MPC 模型需求解复杂的非线性代数微分方程，其模型求解较为复杂。为简化控制模型求解来提高预测控制的时效性，可借助2.1 节的轨迹灵敏度法将MPC 模型转换为二次规划模型进行求解（可采用求解非线性规划的一般方法和求解线性规划的特定解法），大幅降低模型求解的复杂度，快速给定控制元件的动作量来改善暂态电压稳定性。

2.3 两阶段优化控制模型

实施直流送端系统暂态过电压预防控制可降低暂态过电压失稳风险，但有可能出现恢复阶段电压不安全，故需要进行直流送端系统暂态过电压的两阶段优化控制，即暂态过电压的预防控制和恢复阶段电压的预测控制。借助2.1 节轨迹灵敏度法，构建直流送端系统暂态过电压和恢复阶段电压对控制量的轨迹灵敏度，简化传统非线性MPC 控制模型，暂态过电压预防控制和恢复阶段电压预测控制的模型构建过程如下：

1）暂态过电压的预防控制

直流送端系统暂态过电压的预防控制，可从降低暂态过电压幅值和减少暂态过电压持续时间两个方面进行。本文主要考虑抑制暂态过电压幅值，即确保暂态过电压峰值低于1.1(pu)[31]，保证风机不脱网运行，可表示为

式中，Vh.max为节点h的暂态过电压峰值；tcl为故障清除时刻；tlim为故障清除后到暂态过电压峰值出现所经历的时间（文献[11]提出故障切除后70～170ms出现暂态过电压，本文取70ms）；Vlim=1.1(pu)。

通过改变系统初始运行状态，使控制后的暂态过电压峰值低于1.1(pu)，避免风机脱网。暂态过电压预防控制示意图如图3 所示，其中y为被控量，Vh.max(0)和Vh.max(1)分别为控制前、后节点h的暂态过电压峰值。施加暂态过电压预防控制后若出现恢复阶段电压不安全，可通过2.2 节的MPC思想调节控制量，滚动地实施控制直至电压恢复到安全水平。

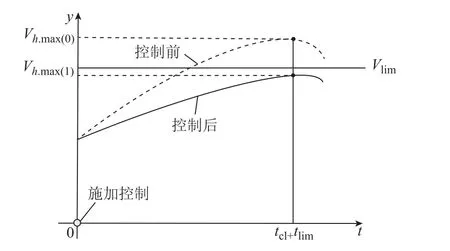
图3 暂态过电压预防控制示意图Fig.3 Schematic diagram of transient overvoltage preventive control

采用2.1 节的交直流系统轨迹灵敏度构建方法，可求取直流送端系统暂态过电压的轨迹灵敏度As。将式（8）和式（9）的原始非线性MPC 数学模型简化为以控制量增量为独立控制变量的二次规划模型，即

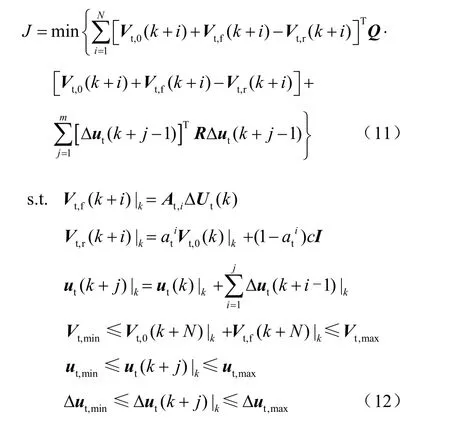
式中，Vt,0、Vt,f和Vt,r分别为暂态过电压的基准值、变化量和目标值，目标函数的第1 项和第2 项分别为控制措施实施代价和节点电压预测偏差的惩罚；At为直流送端系统暂态过电压Vt对控制量的轨迹灵敏 度 矩 阵，可 表 示 为其中Q(o)、VF(p)、kT(q-r)、PH和PW均为暂态过电压控制量，分别代表节点o的电容器无功功率、节点p的发电机机端电压参考值、节点q与节点r之间变压器电压比、直流输电系统的有功功率和双馈风电场的有功功率；ΔUt为所有控制时刻暂态过电压变化量的矩阵；at为设计参数可调节参考轨迹趋近目标值c的快慢程度；I为单位向量；ut和Δut分别为暂态过电压的控制量和控制量的变化量，ut,max、ut,min分别为ut的上、下限，Δut,max、Δut,min分别为Δut的上、下限；Vt,max、Vt,min分别为直流送端系统暂态过电压的上、下限。

由于直流送端系统暂态过电压的动态过程较短，无法直接实施预测控制，可在系统故障前调整控制元件的动作量来预防控制暂态过电压发生。

2）恢复阶段电压的预测控制

在对暂态过电压进行预防控制的同时，若恢复阶段电压不安全，可采用相同原理构建恢复阶段电压的二次规划模型，实现恢复阶段电压的预测控制。

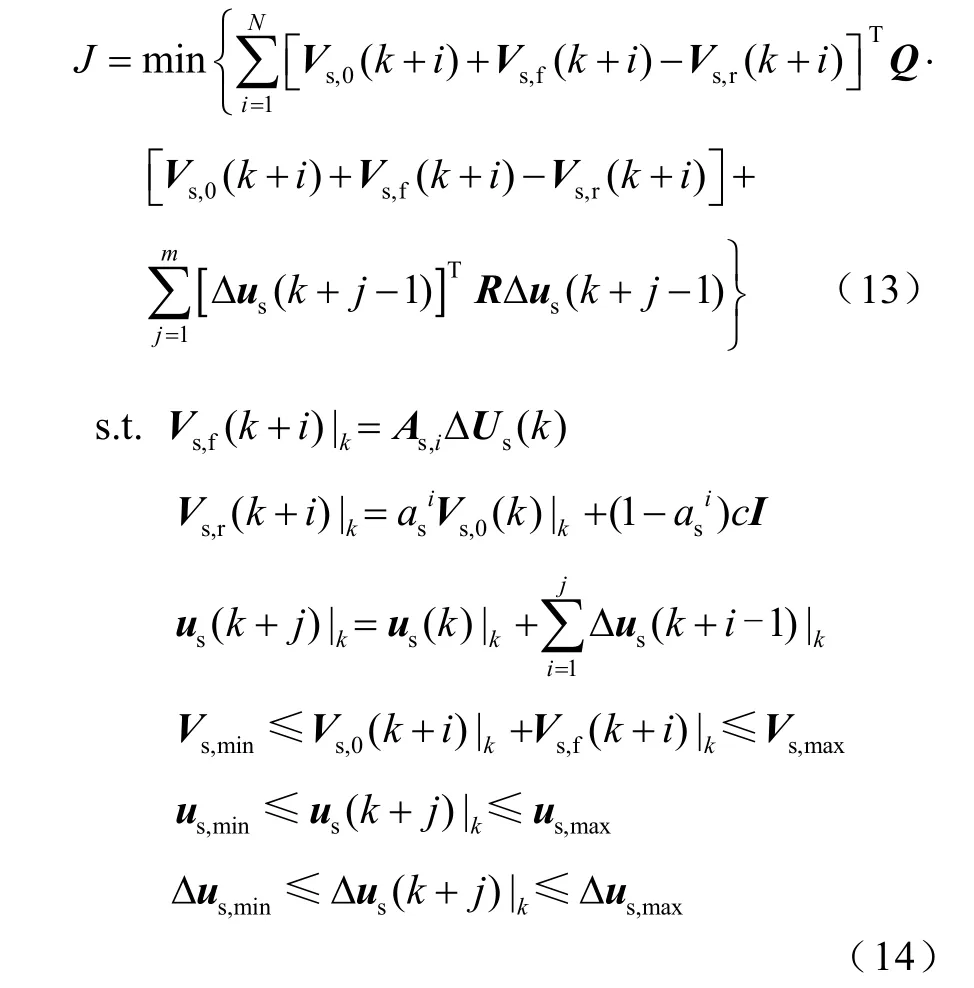
式中，Vs,0、Vs,f和Vs,r分别为恢复阶段电压基准值、变化量和目标值；As为直流送端系统恢复阶段电压Vs对控制量的轨迹灵敏度矩阵，可表示为As=[∂Vs/∂Q(o)∂Vs/∂VF(p)∂Vs/∂kT(q-r)∂Vs/∂PH∂Vs/∂PW]；ΔUs为恢复阶段所有控制时刻电压增量组成的矩阵；as为恢复阶段电压控制的设计参数；us和Δus分别为恢复阶段电压的控制量和控制量的变化量；us,max、us,min分别为us的上、下限；Δus,max、Δus,min分别为Δus的上、下限；Vs,max、Vs,min分别为恢复阶段电压的上、下限。

通过恢复阶段电压的预测控制，可使直流送端系统规避暂态过电压失稳风险的同时，确保后期恢复阶段电压运行在安全范围内。

2.4 控制元件选取

控制元件的选取原则是在直流送端系统暂态过电压预防控制和恢复阶段电压预测控制阶段，分别根据直流送端系统暂态过电压和恢复阶段电压对控制量的轨迹灵敏度确定控制元件投入顺序。当施加某种控制措施后电压未满足要求，则采用其他控制措施进行协调控制。具体方法如下：

（1）设被控节点为直流送端系统节点h，通过时域仿真得到该节点在tk+1时刻的暂态过电压预测值和目标值

（2）根据被控节点h暂态过电压对控制量的轨迹灵敏度和控制元件的最大投入量，计算tk+1时刻节点h的暂态过电压最大控制量ΔVt(k+1)为

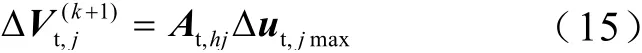
式中，ΔVt,j(k+1)为ΔVt(k+1)的第j个元素；Δut,jmax为暂态过电压预防控制中第j个控制元件的最大投入量；At,hj为节点h暂态过电压对控制量j的轨迹灵敏度，，其中Δut,j为暂态过电压预防控制中第j个控制元件的变化量，和分别为控制量j实施前、后的暂态过电压幅值。

（3）设置控制元件可投入的最大台数，按ΔVt(k+1)中元素由大到小的顺序依次投入，若M（小于最大台数）个控制元件动作后，暂态过电压达到目标值则根据式（16）确定待投入控制元件数目。

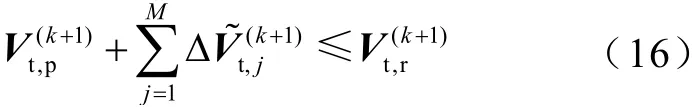
（4）若某种控制元件投入极限台数后，系统暂态过电压未满足要求，则根据轨迹灵敏度由大到小的顺序依次投入其他控制元件，选取方法相似。

（5）若施加控制后恢复阶段电压不安全，则进行恢复阶段电压控制，计算恢复阶段电压不安全节点h对控制量的轨迹灵敏度，并结合式（17）和式（18）选取控制元件，具体实施方法与上文类似，本文不再赘述。

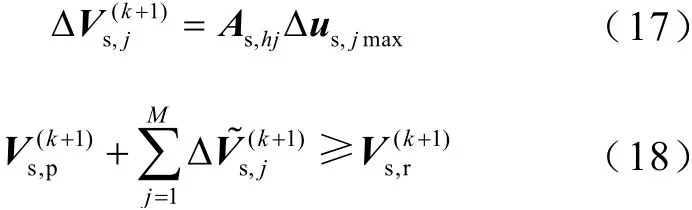
式中，ΔVs,j(k+1)为tk+1时刻节点h恢复阶段电压最大增量ΔVs(k+1)的第j个元素；As,hj为恢复阶段电压不安全节点h对控制量j的轨迹灵敏度；Δus,jmax为控制中第j个控制元件的最大投入量为按从大到小排序后的第j个元素；和分别为恢复阶段电压的预测值和目标值。

2.5 优化控制流程

基于轨迹灵敏度的暂态过电压两阶段优化控制流程如图4 所示。

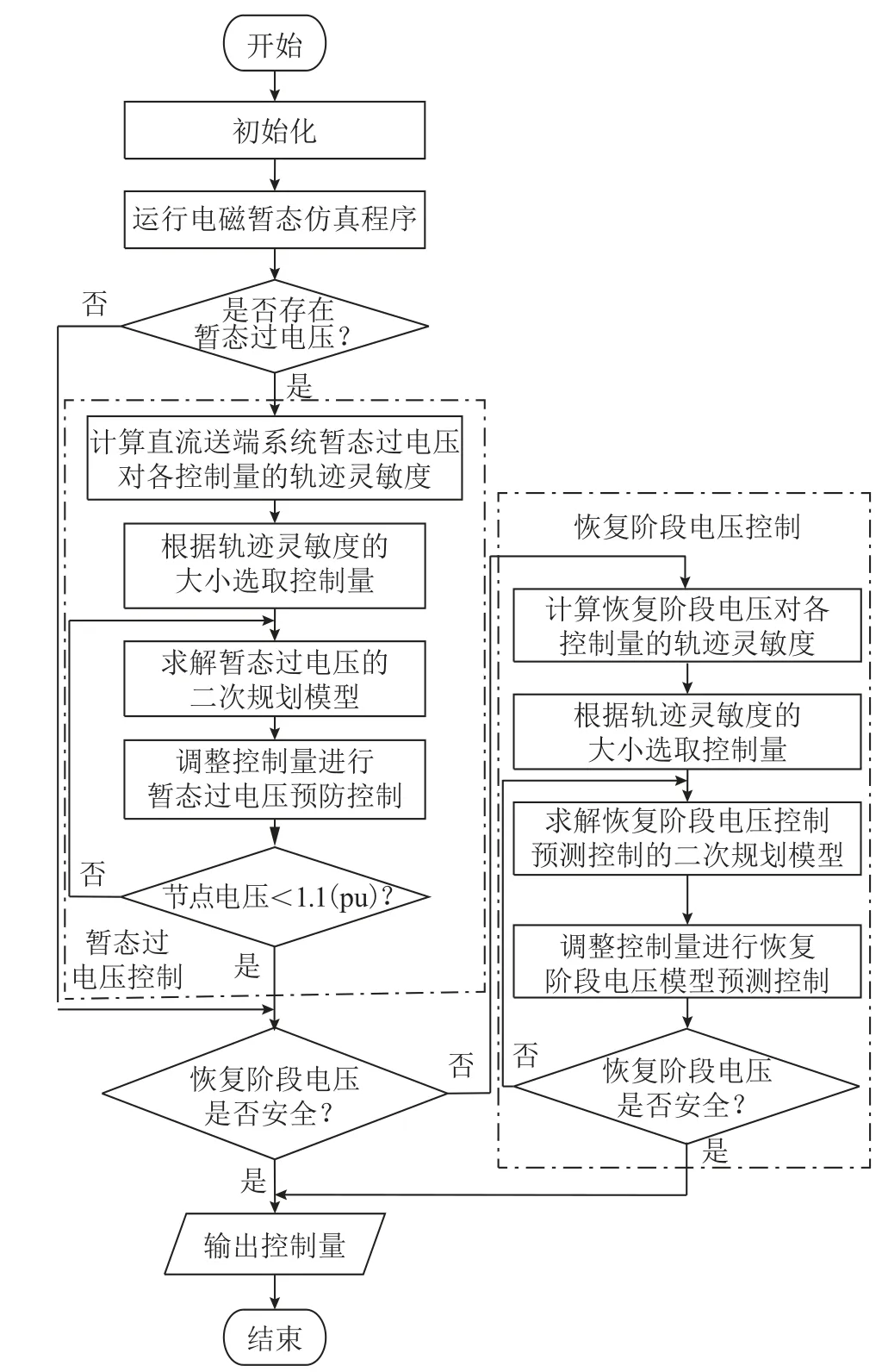
图4 两阶段优化控制流程Fig.4 Flow chart of two-stage optimization control

暂态过电压两阶段优化控制的具体步骤如下：

（1）初始化。设置故障发生和切除时刻，MPC模型参数以及电磁暂态仿真参数。

（2）运行电磁暂态仿真程序。基于电磁暂态仿真得到系统轨迹，计算直流送端系统暂态过电压对各控制量的轨迹灵敏度，根据轨迹灵敏度大小选取控制量。

（3）由式（11）和式（12）将传统MPC 模型转换为暂态过电压预防控制的二次规划模型，并在初始时刻将控制量施加到系统中进行电磁暂态仿真。

（4）判断直流送端系统暂态过电压幅值是否小于1.1(pu)，若未满足，则在下一个控制周期到来时重复步骤（2）和步骤（3）。若满足，则判断恢复阶段电压是否运行在安全范围内；若是，则仿真结束，输出最优控制序列；否则，继续运行步骤（5）。

（5）计算恢复阶段电压不安全节点对各控制量的轨迹灵敏度，根据轨迹灵敏度大小选取控制量。

（6）按式（13）和式（14）将传统MPC 模型转换为恢复阶段电压预测控制的二次规划模型进行求解，并将所得控制序列的第一个优化控制量施加到交直流系统实施滚动优化控制。

（7）判断直流送端系统恢复阶段电压是否安全，安全则仿真结束，输出最优控制序列；否则，在下一个控制周期转到步骤（6）。

3 算例分析

本节以修改后IEEE 39 节点系统为例进行仿真分析。在节点37 接入360 台1.5MW DFIG(采用单机等效模型模拟双馈风电场[32])；在节点2 和节点25 间加入CIGRE 500kV 双极HVDC 输电系统[33]。借助 Simulink/Matlab 搭建仿真模型，仿真步长为5×10-5s（仿真计算机配置：CPU：Core i7-8550U，主频1.80GHz，内存8.00GB）。发电机采用4 阶模型，各发电机上均装设电压调节器，励磁系统采用4 阶模型，负荷采用恒阻抗负荷模型。预测控制模型的初始参数可参考文献[34]。

3.1 暂态过电压的仿真分析

在交直流受端系统节点2 发生三相短路故障，故障开始时刻为8s，故障持续时间为0.1s。未施加控制时的直流送端系统节点25 电压曲线如图5 所示。

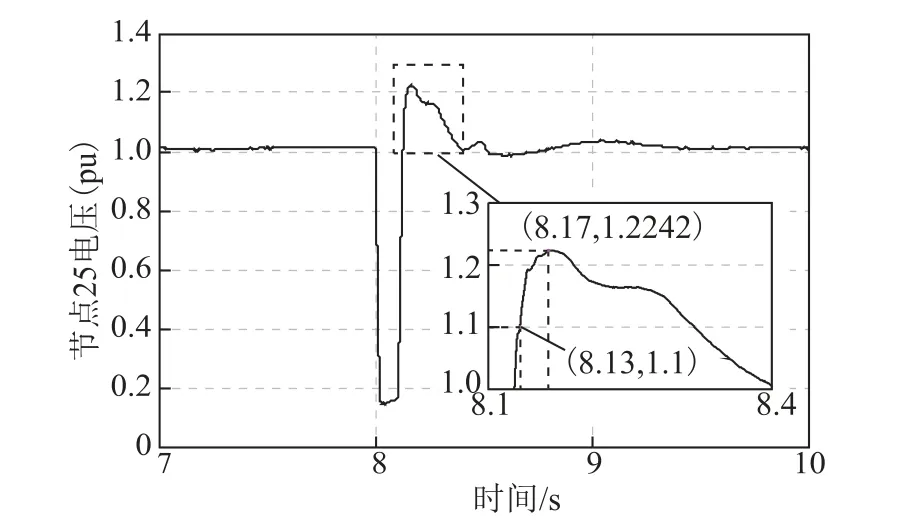
图5 未施加控制时节点25 电压曲线Fig.5 Bus 25 voltage curve without control

由图5 可知，在t=8.1s 故障清除后，交直流送端系统节点25 的电压逐渐上升，若不施加任何控制，在t=8.13s 时电压值达到1.1(pu)，节点25 开始出现暂态过电压现象，并在t=8.17s 时暂态过电压达到最大，暂态过电压峰值为1.224 2(pu)。

3.2 暂态过电压的预防控制

采用所提控制措施对直流送端系统暂态过电压进行预防控制，在t=0s 时预防控制动作对系统实施电压控制，以保证节点25 电压在1.0(pu)～1.10(pu)的范围内。本文借助暂态过电压对各控制量的轨迹灵敏度选取关键控制元件。为说明轨迹灵敏度用于暂态过电压预防控制的准确性，以节点20 的电容器为例进行仿真分析，电容器容量与暂态过电压峰值的对应关系如图6 所示。

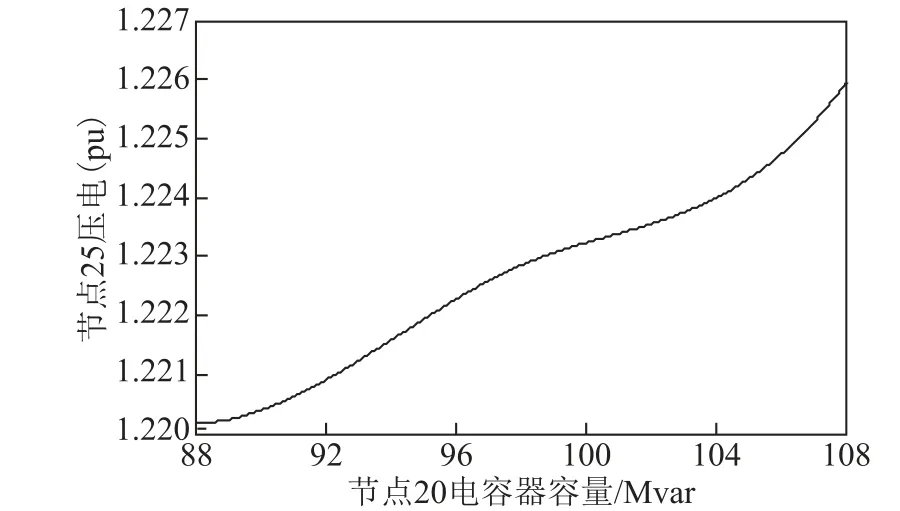
图6 电容器容量对暂态过电压的影响Fig.6 Effect of capacitor capacity on transient overvoltage

由图6 可知，节点20 所连电容器容量在区间[88Mvar，108Mvar]变化时，与暂态过电压峰值的灵敏度呈线性变化，而在暂态过电压预防控制中节点20 所连电容器的变化区间为92～103Mvar，均在灵敏度的线性区间，进而证明将轨迹灵敏度应用于暂态过电压预防控制的可行性和准确性。

节点25 暂态过电压对各控制量的轨迹灵敏度如图7 所示。由灵敏度大小确定参与控制的元件为：节点4、20、27、28、29 的电容器，节点30、32、35、38、39 的励磁调节器，变压器2-30、29-38、6-31、10-32、21-33，直流输电系统和双馈风电机组。其中，电容器每次优化的最大控制变化量为10Mvar，最大控制量为20Mvar，每次优化最多动作台数为5 台；发电机机端电压每次优化的最大控制变化量为0.04(pu)，最大控制量为0.06(pu)，每次优化最多动作台数为5 台；变压器电压比每次优化的最大控制变化量为0.005(pu)，最大控制量为0.006 7(pu)，每次优化最多动作台数为5 台；HVDC 系统传输的有功功率每次优化的最大控制变化量为70MW，最大控制量为100MW；风电场有功功率每次优化的最大变化量为30MW，最大控制量为45MW。

由图7 可知，节点25 暂态过电压峰值对变压器电压比kT和发电机机端电压参考值VF的轨迹灵敏度，较HVDC 系统传输的有功功率PH、风电场的有功功率PW和电容器无功功率Q的轨迹灵敏度大，即kT和VF对节点25 暂态过电压峰值的影响程度较PH、PW、Q高。因此在施加控制时，优先投入kT和VF，若未满足控制要求再依次投入PH、PW和Q。

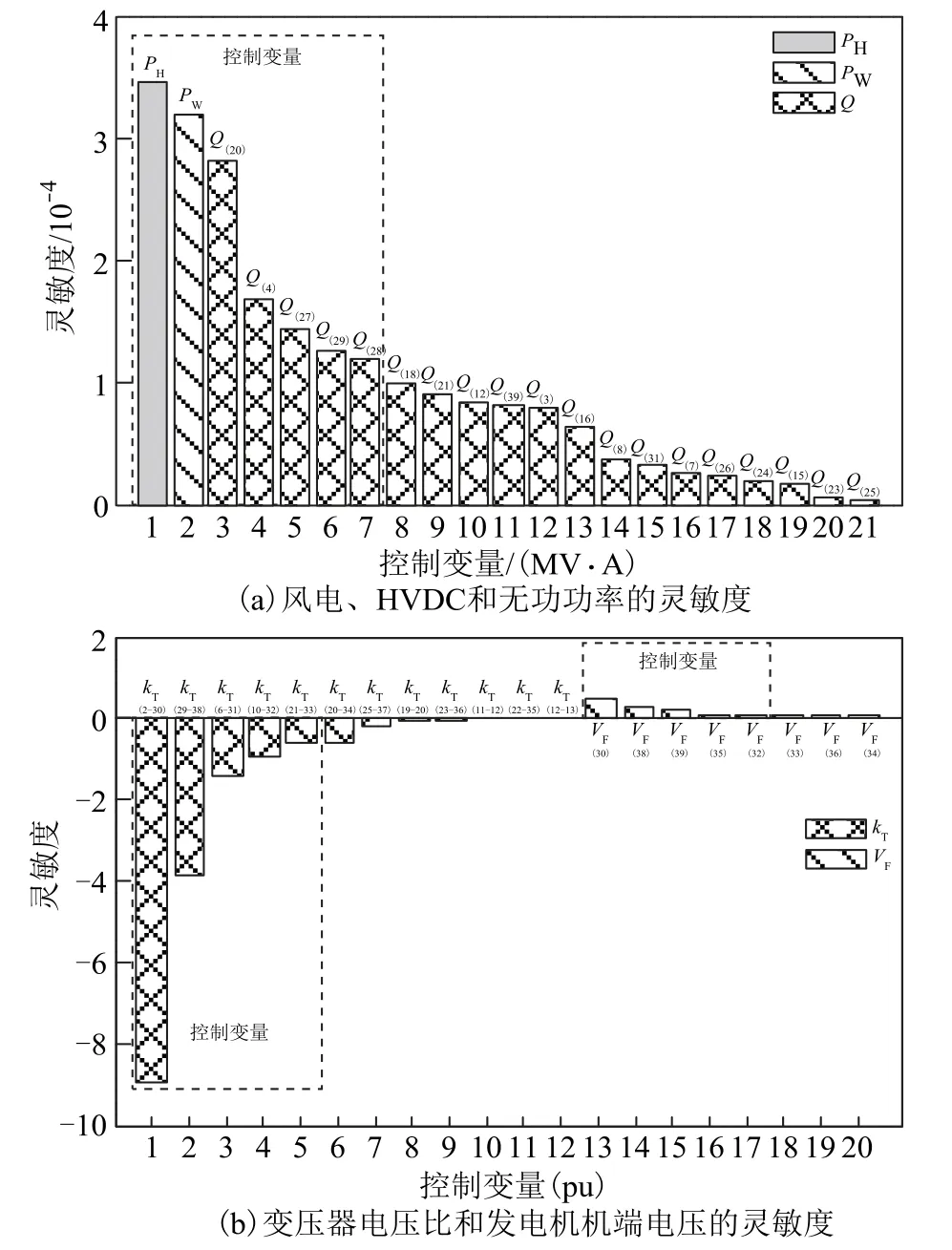
图7 节点25 暂态过电压峰值对控制量的轨迹灵敏度Fig.7 Trajectory sensitivity of bus 25 transient overvoltage peak to selected control quantity

经直流送端系统暂态过电压预防控制后的控制量变化值情况见表1。将各控制量施加到交直流系统后，可得直流送端系统节点25 电压的曲线如图8所示。

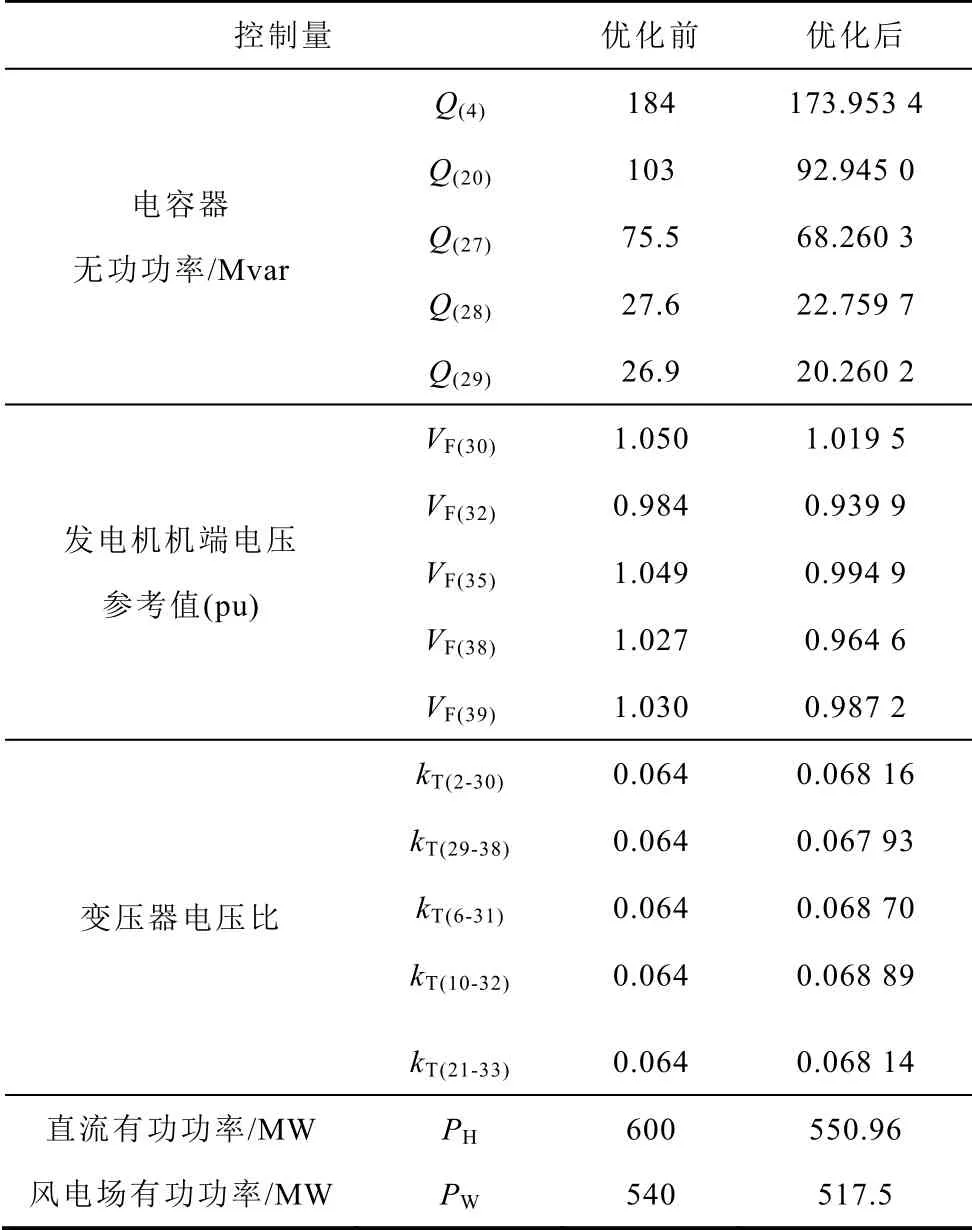
表1 暂态过电压预防控制的控制量变化值情况Tab.1 Values of control variables after transient overvoltage prevention control

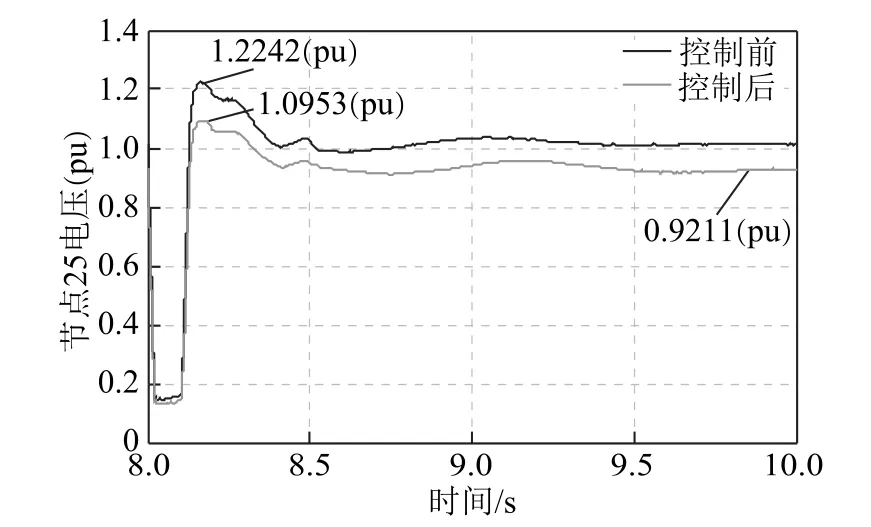
图8 施加预防控制后节点25 电压曲线Fig.8 Bus 25 voltage curve with prevention control

由图8 可知，将预防控制施加到交直流混合系统后，节点25 的暂态过电压峰值由1.224 2(pu)降到1.095 3(pu)，即将暂态过电压峰值限制在1.1(pu)以下，避免风机脱网风险，由此可验证本文所提方法的有效性。交直流系统部分节点暂态过电压峰值见表2。

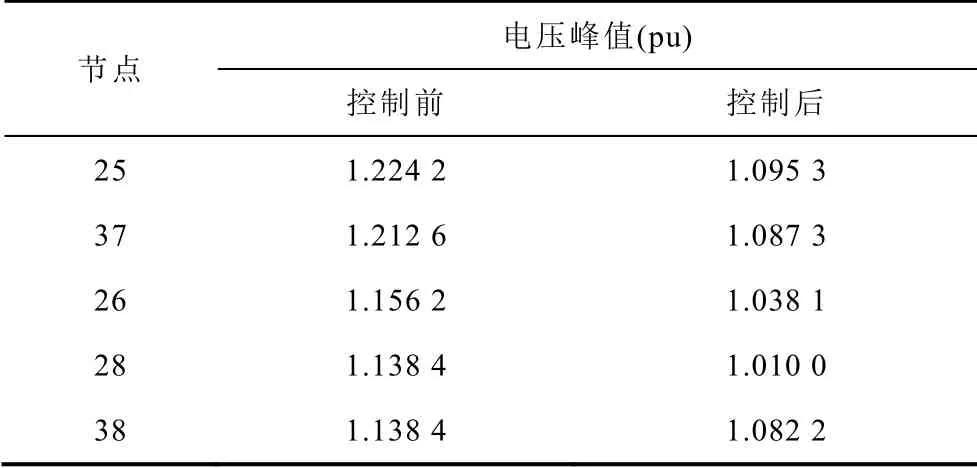
表2 其他节点的暂态过电压峰值Tab.2 Transient overvoltage peak of other nodes

由表2 可知，在直流送端系统暂态过电压最严重的节点25 进行预防控制后，交直流系统的暂态过电压现象得以消除，进一步验证所提方法的可行性。

3.3 恢复阶段电压的预测控制

由3.2 节的图8 可知，在直流送端系统施加暂态过电压的预防控制后，节点25 的恢复阶段电压跌落至0.921 1(pu)，超出电压的安全运行范围。需启动本文所提直流送端系统恢复阶段电压预测控制，以确保节点25 的恢复阶段电压运行在安全范围内。同样由节点25 的恢复阶段电压对各控制量的轨迹灵敏度大小，确定参与控制的元件为节点27、12、20、23、31 的电容器，节点30、38、39、32、26 的励磁调节器，变压器2-30、25-37、29-38、21-33、22-35，直流输电系统和双馈风电机组。控制元件的最大投入量确定方法同3.2 节，而且控制元件施加顺序依然是优先投入kT和Vref，若未满足控制要求，再依次投入PH、PW和Q。将暂态过电压恢复阶段预测控制方法与基于准稳态方程的非线性 MPC（Nonlinear Model Predictive Control, NLMPC）[35]方法进行对比分析。为保证其可比性，选取相同的控制量，经交直流送端系统恢复阶段电压预测控制模型的优化求解，获得两种优化控制方法下第1 个控制周期各控制量的变化量见表3。

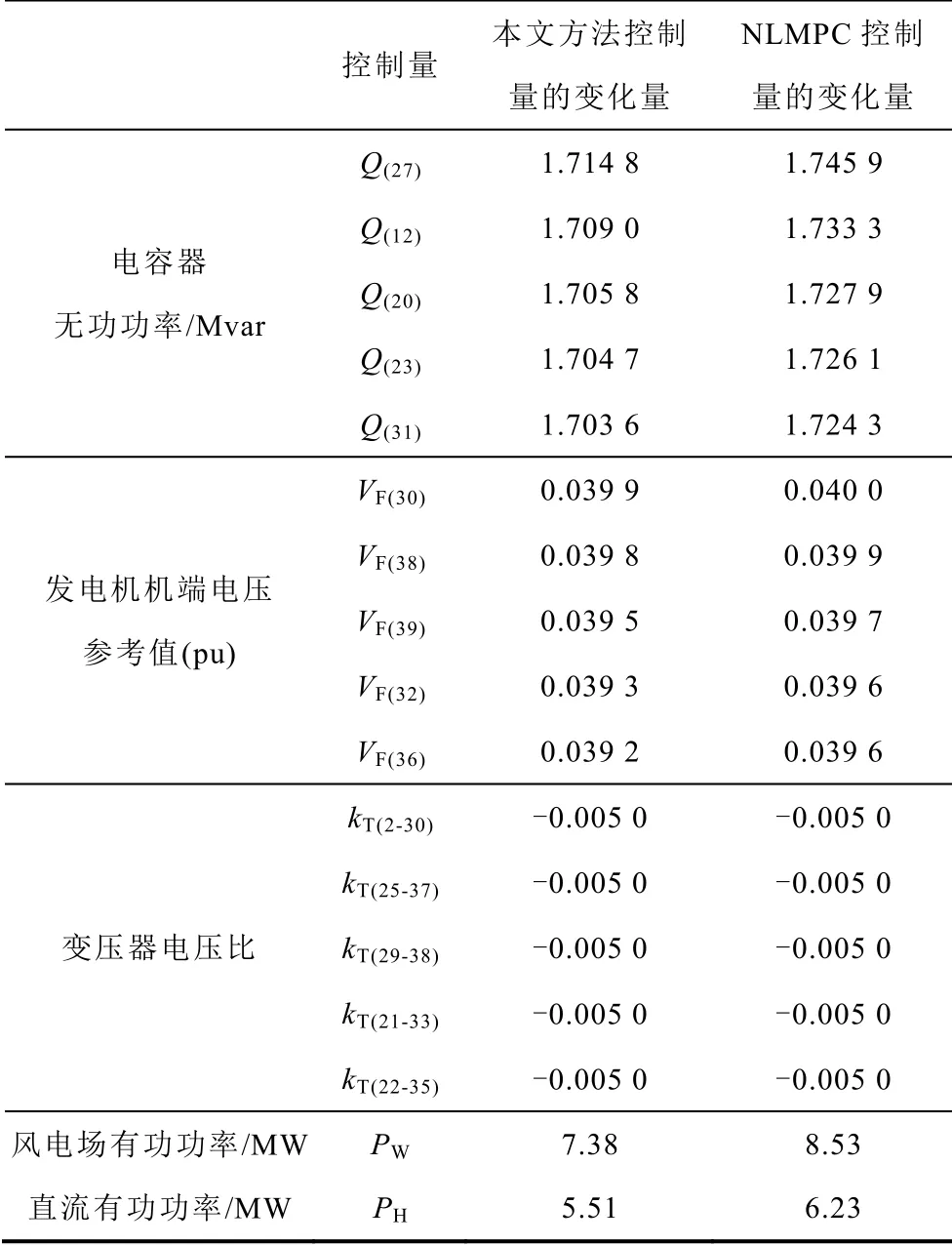
表3 第1 个控制周期各控制量的变化量Tab.3 Variation of each control variable in the first control period

借助电磁暂态仿真来模拟预测控制的实时滚动优化控制效果，并对比分析未施加任何控制、施加暂态过电压预防控制、施加恢复阶段电压第1 次控制时的直流送端系统节点25 的电压变化情况。在t=11s时，将预测控制模型优化求解的第1 控制周期各控制量施加到交直流系统，得到施加第1 次控制后直流送端系统节点25 的电压曲线如图9 所示。而本文方法与NLMPC 的电压曲线变化如图10 所示。

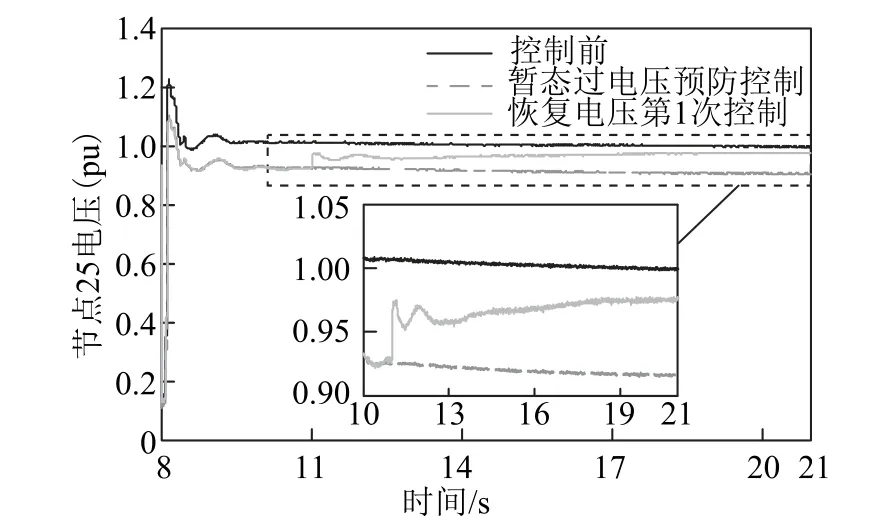
图9 第1 次控制后节点25 电压Fig.9 Voltage of node 25 after the first control

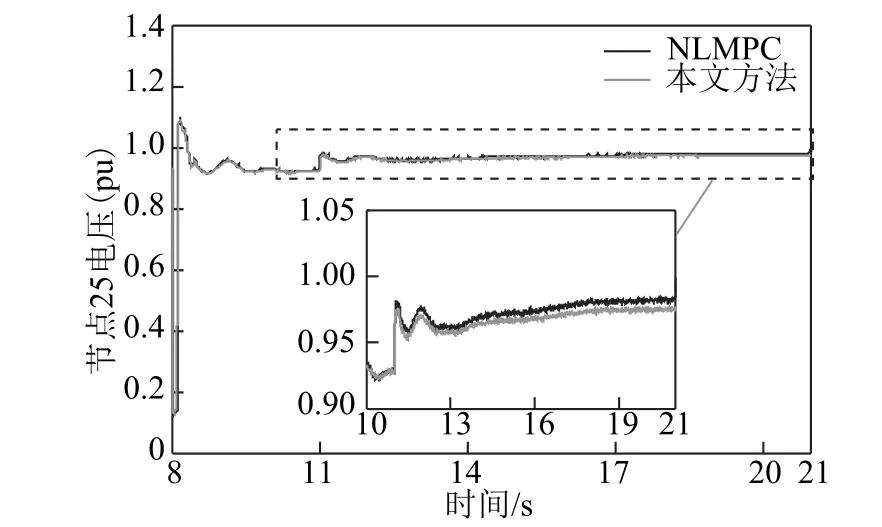
图10 不同控制方法的电压曲线Fig.10 Voltage curves of different control methods

由图9 和图10 可知，本文所提恢复阶段电压预测控制在t=11s 时将第1 周期控制量施加到交直流系统，节点25 的恢复阶段电压值由0.921 1(pu)提高到0.973 8(pu)，经NLMPC 控制后恢复阶段电压由0.921 1(pu)提高到0.975 2(pu)，预测结果具有更高的准确性。在优化时间方面，本文方法的优化时间为1.093s，而NLMPC 需在预测时域内反复进行时域仿真求取最优控制序列，其优化控制求解速度较慢。综上，由于两种方法第1 周期控制均未使恢复阶段电压达到1.0(pu)，都需要进行第2 周期控制。进一步通过恢复阶段电压预测控制模型的优化求解，获得第2 个控制周期各控制量的变化量，见表4。

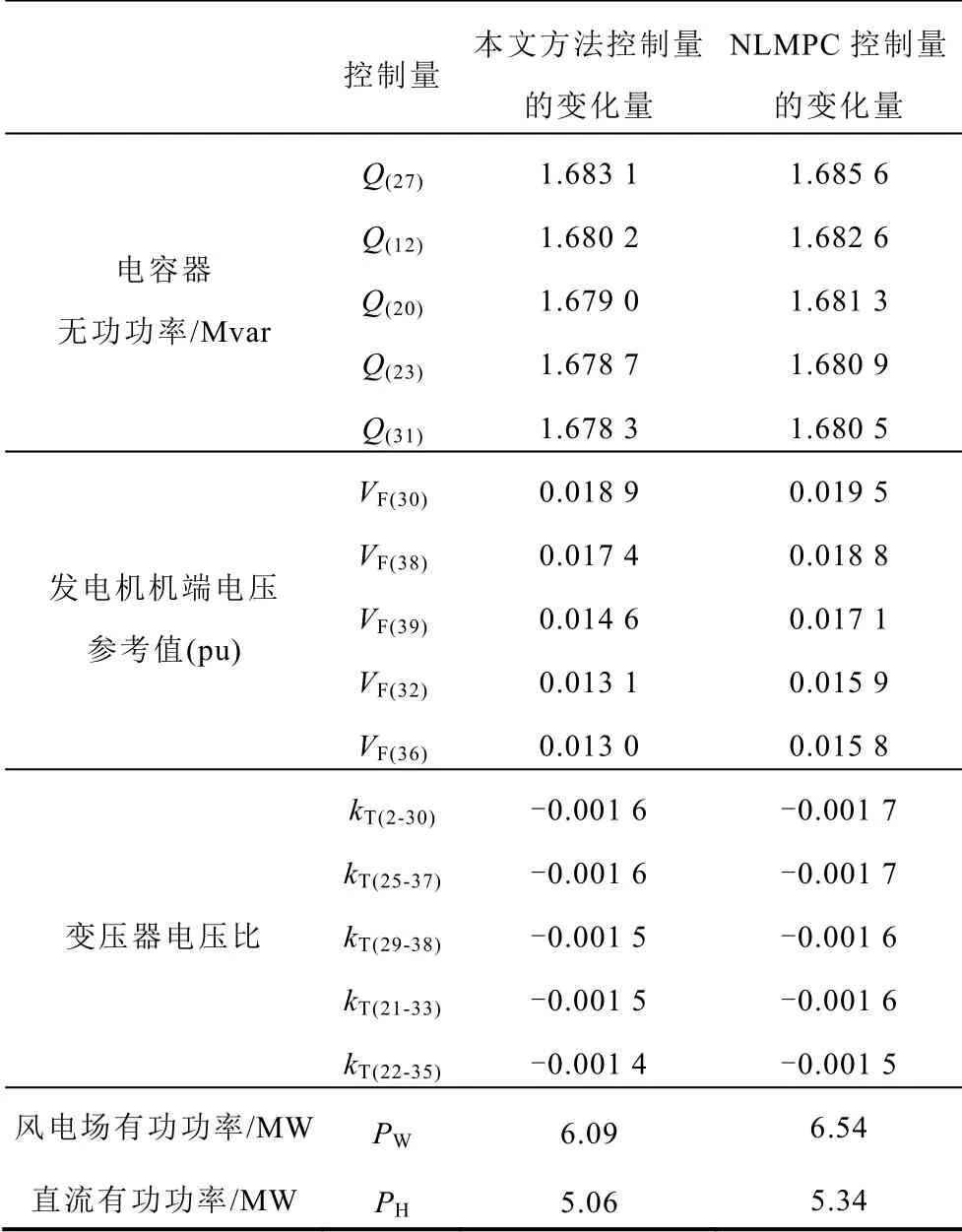
表4 第2 个控制周期各控制量的变化量Tab.4 Variation of each control variable in the second control period

当t=21s 时将预测控制模型优化求解的第2 控制周期各控制量施加到系统中，获得本文方法在第2 次控制后节点25 的电压曲线，如图11 所示。本文方法与NLMPC 的电压曲线变化如图12 所示。

图11 第2 次控制后节点25 电压Fig.11 Voltage of node 25 after the second control

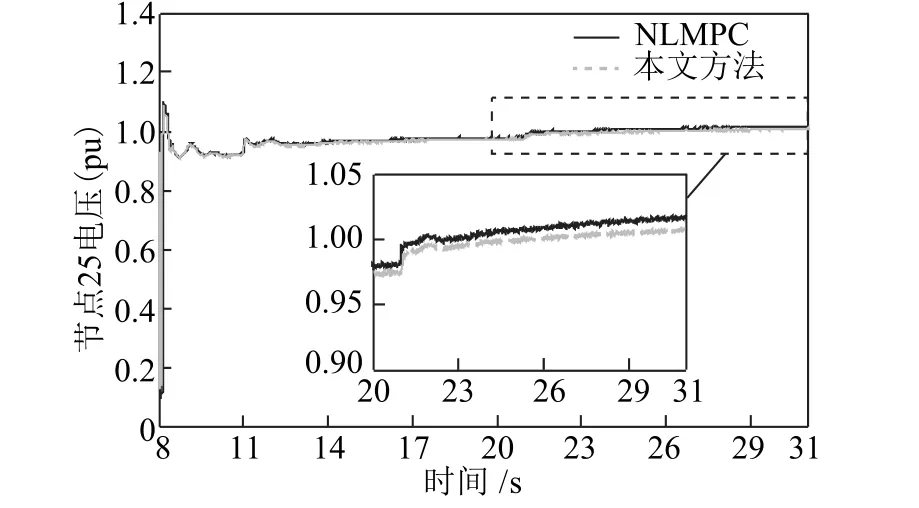
图12 不同控制方法的电压曲线Fig.12 Voltage curves of different control methods

由图11 和图12 可知，本文方法可使节点25 恢复阶段电压值由0.973 8(pu)提升到1.009 8(pu)，优化时间为1.091s。LMPC 可将节点25 恢复阶段电压值由0.975 2(pu)提升到1.011 5(pu)。可见两种方法都可使预测电压达到目标值，即本文所提预测控制方法可使恢复阶段电压运行在安全范围内，进而验证所提方法的有效性。

进一步对比分析施加恢复阶段电压预测控制后，直流送端系统其他节点恢复阶段电压值的变化情况见表5。

表5 其他节点的恢复阶段电压Tab.5 Recovery voltage of other nodes

由表5 可知，将第1 周期控制量施加到系统后，两种优化控制方法节点25、37、26 的恢复阶段电压仍低于1.0(pu)，未达到预期控制目标值。第2 周期控制量施加到系统后，所有节点的电压均在1.0(pu)以上，达到预期电压控制效果，且本文方法恢复阶段电压预测控制的平均优化时间为 1.092s，相比NLMPC 方法可大幅度减少优化求解所需时间，由此进一步验证所提控制方法的有效性。

4 结论

本文提出一种基于轨迹灵敏度的暂态过电压两阶段优化控制方法。通过修改后IEEE 39 节点系统的算例分析可知，借助直流送端系统暂态过电压和恢复阶段电压对控制量的轨迹灵敏度，将传统MPC优化模型转换为以控制量增量为独立变量的二次规划模型，与NLMPC 方法相比具有较快的模型求解速度，并充分发挥直流和风电有功控制量对暂态过电压和恢复阶段电压的调节作用。

在暂态过电压两阶段优化控制中，直流送端系统暂态过电压预防控制能将暂态过电压峰值限制在1.1(pu)以下降低风机脱网风险，恢复阶段电压的预测控制可将恢复阶段电压不安全节点调整到电压安全范围1.0(pu)附近，从而兼顾直流送端系统暂态过电压和恢复阶段电压的安全稳定性，可为调度人员的暂态电压稳定控制提供参考。