计及多个风场预测误差的电力系统风险快速计算方法

张 沛 田佳鑫 谢 桦

（北京交通大学电气工程学院 北京 100044）

0 引言

受能源转型的需求及国家政策影响，新能源并网规模越来越大，但大规模风电的波动性会给电网的调度运行带来风险，所以需要对电网运行开展量化风险评估。因此，风险的计算方法的研究显得尤为重要。

电力系统风险计算方法主要有四种：点估计法、状态枚举法、蒙特卡洛法和半不变量法。在点估计法和状态枚举法的研究方面，文献[1-3]均采用点估计法来计算系统的运行风险，构建系统风险指标与可用电源输出随机变量的函数关系，从随机变量中选取少量估计点进行函数运算，进而求得风险指标。点估计法虽然在计算风险指标时有较快的速度，但是当系统规模较大时，输出随机变量的高阶距和概率分布误差增加，其实用性与准确性会降低，还需进一步考证。文献[4]中所列举的状态枚举法，通过对系统出现的所有状态逐一枚举并进行潮流计算，进而得出风险，使用该方法进行风险计算时，结果固然准确，但当系统中接入多个风场时，基于状态枚举的方法计算运行风险时会出现系统状态组合爆炸的问题。例如，某电力系统中风场数量为n，每一风场的出力区间为Ni，则系统的状态数为，采用枚举法计算运行风险时不仅需要进行次潮流计算，还需要在每一次潮流计算结果的基础上计算运行风险，耗费大量时间，无法满足调度运行的时效性。

在蒙特卡洛法的研究方面，文献[5]采用改进的分散抽样蒙特卡洛法，其中等分散抽样仅仅在处理多状态元件上具有较高的抽样效率，可以加快计算的收敛速度；文献[6]采用传统的非序贯蒙特卡洛法来计算风险，其中风场预测误差运用TLS（T-location scale）拟合，具有好的拟合效果，文献中提出切负荷、电压越限、线路有功越限及电压崩溃等风险指标，全方面地评估系统运行风险；文献[7]采用蒙特卡洛模拟法评估光伏并网系统的时变风险，通过失负荷概率和期望缺供电量风险指标来评估风险水平；文献[8-10]均采用非序贯蒙特卡洛法建立电力系统的运行风险评估模型，较序贯蒙特卡洛法而言，该算法具有需求内存少、模型简单及收敛快的优点。文献[5-10]都采用蒙特卡洛法或者蒙特卡洛的改进算法，要进行大规模抽样才能保证其准确度，但会导致计算效率下降。这些方法虽然提高了状态抽样的效率，可以加快收敛速度，但是无法避免大量重复的潮流计算，计算周期长，内存消耗大，不利于电力系统的实时调度运行。

半不变量法是根据潮流计算结果构建输出随机变量和输入随机变量的线性化关系，在此基础之上，利用半不变量的性质计算出输出随机变量的半不变量，结合级数展开理论得到输出随机变量的概率分布函数。文献[11]采用半不变量法计算线路随机故障下的运行风险，同时改进了分布式电源的随机模型，但仅应用于小型配电系统，针对大型主电网的风险计算并没体现；文献[12]在快速解耦的潮流模型基础上采用半不变量的改进Von Mises 方法计算运行风险，加快了计算速度，但该方法是建立在快速解耦法之上，因而前提为电抗远大于电阻，这一条件不是所有电力系统都能满足，因此存在一定的局限性；文献[13]先采用基于序列运算理论实现随机潮流计算，之后将随机潮流引入安全评估，通过概率与风险两个角度来实现风险的量化。文献[11-13]均采用半不变量法或者其改进算法，虽然避免了大量重复的潮流计算，提高了计算效率，但输入随机变量波动范围较大时，计算结果会产生较大线性化误差。文献[14]对这种误差进行了研究和说明。同时由于这种线性化误差的存在会导致输出随机变量的概率分布发生局部畸变，使得风险评估结果准确度不能够达到实时调度运行的要求。

针对上述不足，本文提出快速计算运行风险的方法，可以快速计算含有多个风场预测误差的电力系统的运行风险。本文所提方法在半不变量法基础之上加入了聚类技术。在该方法中，考虑风电预测误差的节点注入功率（简称节点注入功率）作为输入随机变量，节点电压与支路潮流作为输出随机变量。基于K-means 聚类技术对输入随机变量样本进行聚类，以降低样本的波动范围。针对每一簇类进行潮流计算，根据潮流计算结果构建输出随机变量与输入随机变量的线性化关系，并结合半不变量的性质计算输出随机变量的K阶半不变量，进而采用Gram-Charlier 级数展开理论计算输出随机变量累积分布函数（Cumulative Distribution Function, CDF）。根据CDF 曲线，对越限部分进行积分运算求得运行风险，并计算其运行风险指标。经过聚类处理后，输入随机变量样本的波动范围大大减小，在每一类簇中采用半不变量法相比整个样本采用半不变量法得到的线性化关系更加准确，提高了运行风险评估结果的准确性。

1 考虑风场预测误差波动的潮流线性化关系构建

本文考虑多个风场于不同节点同时并网的运行工况，计及预测误差的风场出力作为系统的输入随机变量。在该运行工况，由于风电预测误差的波动范围较大，所以每个风机并网点的风场出力也具有较大的波动性。由于这种波动性的存在，以风场出力期望值代入系统得到的潮流线性化关系进行风险计算会产生较大的线性化误差，因此本文提出采用K-means 对输入随机变量样本进行聚类，建立每一簇类样本对应的潮流线性化关系，可以降低每一簇类内风场出力的波动性，减小线性化误差。

1.1 输入随机变量的概率分布

输入随机变量是风场出力，其中风场出力是风场预测功率与预测误差之和，故输入随机变量的概率分布与风场预测误差的概率分布相同。其中，由于风场之间存在一定的差异，所以不同风场预测误差的概率分布也不同。本文风场预测误差的概率分布是根据某地区风场出力实际功率与预测功率的差值进行统计计算而来，因此更符合实际运行工况。

由于输入随机变量之间相互独立是使用半不变量法的前提条件，因此输入随机变量之间需要进行相关性处理。根据文献[15-16]中的Cholesky 分解去除多个输入随机变量之间的相关性。根据输入随机变量的概率分布，并进行相关性处理后，生成符合该分布的样本，可表示为

式中，Xwind为输入随机变量样本；xij为第j个随机变量中第i个样本的数值；m为输入随机变量的数量；N为每个输入随机变量中样本数量。

1.2 基于K-means 技术的样本聚类

为了减小由风场出力波动性较大而造成的线性化误差，采用K-means 技术[17-18]将输入随机变量聚为多簇类。其聚类过程如下：

（1）选取初始聚类中心。为了保证能够得到较好的聚类效果，针对输入随机变量样本Xwind而言，随机选取10%的样本进行聚类，得到a个聚类中心，即

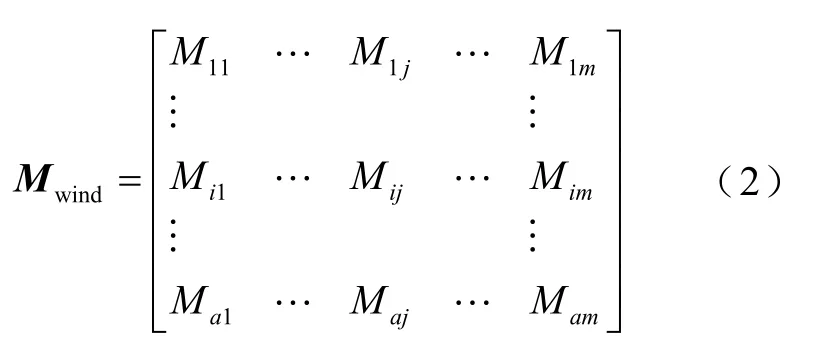
式中，Mwind为聚类中心矩阵；Mij为第j个输入随机变量第i簇类的聚类中心。通过该方式得到的聚类中心可以反映整个样本的分布情况，且可以提高聚类效率。因此，将这10%样本的聚类中心作为初始聚类中心。

（2）计算所有点到聚类中心的欧式距离。欧式距离D为

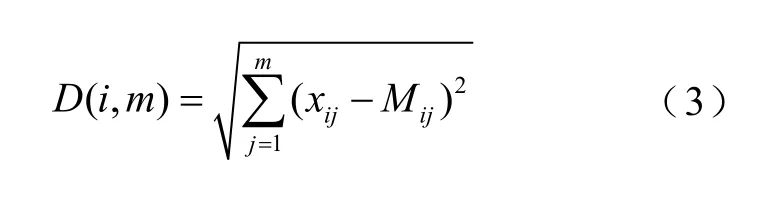
（3）计算簇中样本均值并更新聚类中心。根据欧式距离大小，更新每一簇类中的点，并计算簇类中样本均值，更新聚类中心Mwind。

（4）重复步骤（2）、步骤（3）直到簇类中的点和聚类中心不发生改变，将最后一次得到的聚类中心作为输入随机变量的聚类中心。

1.3 潮流线性化关系的建立

针对多个风场并网的系统，将输入随机变量经过K-means 聚类后形成的聚类中心Mwind代入系统进行a次潮流计算。根据每次潮流计算结果，得到每一簇类样本下的潮流线性化关系。以某一簇类为例，其计算方法如下。

电力系统的潮流方程[15,19]为

式中，f(·)为潮流方程；S为节点注入功率向量；V为节点电压向量。在该簇类的中心处，应用泰勒级数对式（4）展开，可得该运行点处的潮流线性化关系为

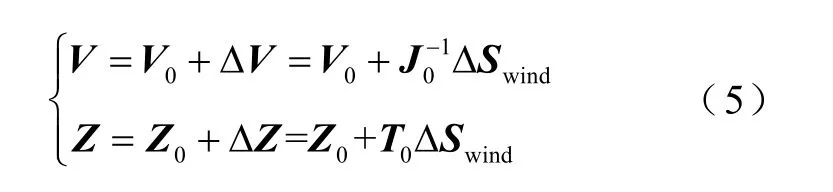
式中，Z为支路功率向量；V0和Z0分别为当前运行点处的节点电压和支路功率向量；ΔV和ΔZ分别为节点电压和支路功率的变化向量；和T0分别为节点电压和支路功率对节点注入功率的灵敏度矩阵；ΔSwind为节点注入功率的变化向量。

由于输入随机变量样本具有较大的波动性，采用整个样本的期望值计算潮流线性化关系误差较大，不能完全满足整个样本的波动特性。因此基于Kmeans 技术将输入随机变量样本聚为a类，在每一类中，样本的波动性会大大降低，其构建的潮流线性化关系更加符合该类样本的波动特性，使得线性化误差大大减小，解决了文献[11-13]中的线性化误差问题。

2 输出随机变量概率分布的计算方法

基于K-means 技术对输入随机变量样本聚类的结果，针对每一簇类而言，通过式（5）可以得到输入随机变量与输出随机变量之间的线性化关系，根据线性化关系可以计算出输出随机变量的概率分布。在这一过程中，对聚类后的每一类簇中应用半不变量法，将复杂的卷积运算简化为加法运算，依次计算输入随机变量和输出随机变量的半不变量，并采用级数展开的方式计算输出随机变量的概率分布，不仅降低了计算的复杂程度，而且K-means 聚类方法的使用解决了使用传统半不变量法时由于输入随机变量波动大而导致线性化误差的问题，使输出随机变量概率分布更加准确，提高了风险计算的精度。

2.1 输入随机变量半不变量的计算方法

根据聚类结果，采用式（6）[20]可以计算每一簇类样本对应输入随机变量的k阶半不变量

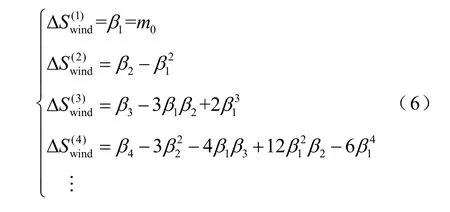
式中，m0和β分别为经过聚类后簇中样本的均值和原点矩。β的计算公式为

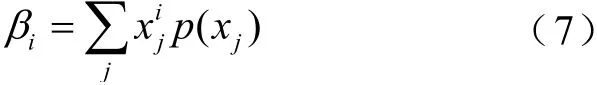
式中，xj为簇类中的样本；p(xj)为xj的概率。

2.2 输出随机变量半不变量的计算方法

以每一簇类样本作为研究对象，式（5）中的ΔSwind需要通过各风场预测误差的概率分布卷积计算得到，运算复杂。利用半不变量的性质可以将卷积运算简化为加法运算，故每一簇类样本对应的输出随机变量半不变量计算公式为

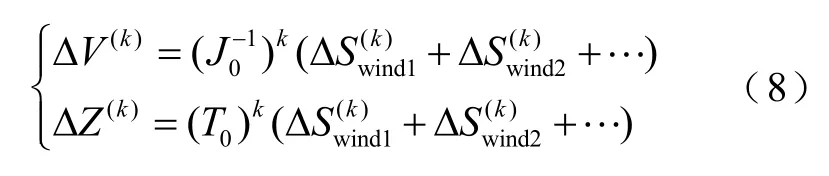
式中，ΔV(k)为当前簇类样本对应的节点电压k阶半不变量；ΔZ(k)为当前簇类样本对应的支路潮流k阶半不变量。

将每一簇类样本对应的输入随机变量半不变量代入式（8）中，可以计算该簇类样本对应的输出随机变量半不变量。

针对全样本而言，计算输出随机变量的半不变量方法如下：

（1）计算全概率值。计算各簇类样本数量占总样本数量的概率。

（2）计算各簇类样本的原点矩。根据式（6）计算各簇类样本对应的各阶原点矩。

（3）计算全样本的原点矩。将各簇类样本的原点矩与全概率值对应相乘并累加得到全样本的原点矩。

（4）计算全样本下的输出随机变量半不变量。将全样本的原点矩代入式（6）中，计算全样本下的输出随机变量半不变量。

2.3 输出随机变量累积分布的计算方法

在输出随机变量半不变量已知的状况下，本文采用级数展开法计算输出随机变量的累积分布函数。目前，常用的级数展开方法有Gram-Charlier 级数展开、Edgeworth 级数展开和Cornish-Fisher 级数展开。其中，Cornish-Fisher 级数展开对非正态分布变量更加准确，且展开的多项式中是以随机变量的分位数作为系数，而本文采用的是半不变量，故不采用Cornish-Fisher 级数展开法；Edgeworth 级数展开在随机变量的CDF 和PDF 尾部存在较大误差；Gram-Charlier 级数展开却具有较高的精度[21]，且节点电压越上限和支路潮流越限一定出现在输出随机变量CDF 曲线的尾部，若该部位出现较大误差，其运行风险的计算结果也会有较大误差。由此可见，Gram-Charlier 级数展开法比Edgeworth 级数展开法更加合适。因此本文采用Gram-Charlier 级数展开法[22]计算输出随机变量的累积分布函数。

Gram-Charlier 级数展开求取输出随机变量的概率密度函数f(x)，即

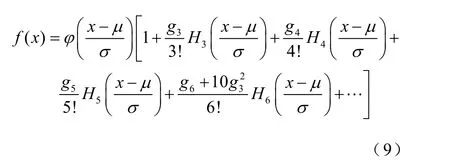
式中，ϕ(·)为标准正态分布的概率密度函数；μ为输出随机变量的期望值；σ为输出随机变量标准差；gk为输出随机变量标准化后的k阶半不变量；Hk(·)为Hermite 多项式[23-24]。

对式（9）进行积分运算可得出输出随机变量的累积分布函数F(x)，即

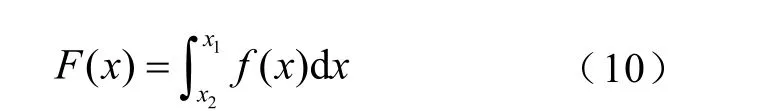
式中，1x和2x分别为积分上、下限。

将节点电压和支路潮流的各阶半不变量代入式（10），可以计算相应的概率分布函数。

3 运行风险指标计算和评估流程

3.1 运行风险评估指标的计算方法

系统运行风险是通过风险发生概率与产生影响的乘积来综合表征。其中，产生的影响在电力系统中体现为两方面：节点电压越限和支路潮流越限。因此，本文采用节点电压越限指标和支路潮流越限指标来定量评估系统的运行风险。在计算运行风险时，本文提出采用积分运算理论，对CDF 曲线中越限部分进行积分运算求得风险，进而计算运行风险指标。

3.1.1 节点电压越限风险指标

节点电压越限风险指标是对系统在一定条件下发生越上、下限的度量。根据电力系统运行导则可知，110kV 及其以下的节点电压的限值范围为0.9(pu)～1.1(pu)，220kV 及其以上的节点电压的限值范围为0.95(pu)～1.05(pu)。以220kV 以上的电压等级为例，节点电压的越限风险指标计算如下。

节点电压的 CDF 曲线如图 1 所示。若Vimin≥0.95(pu)且Vimax≤1.05(pu)时，节点电压越限风险为0；若Vimin或Vimax不在0.95(pu)～1.05(pu)之间，节点电压越限风险为图1 中阴影面积之和，计算方法为

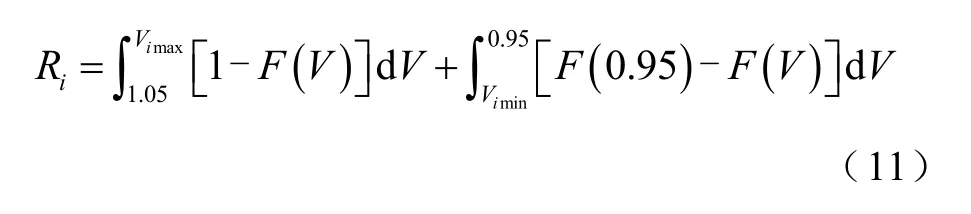
式中，Vimin为第i节点电压可能出现的最小值（即图1 中累计概率刚好大于零所对应的电压值）；Vimax为第i节点电压可能出现的最大值（即图1 中累积概率刚好等于1 时所对应的电压值）；Ri为节点i的电压越限风险。针对具有n个节点的电力系统，系统的节点电压越限风险指标

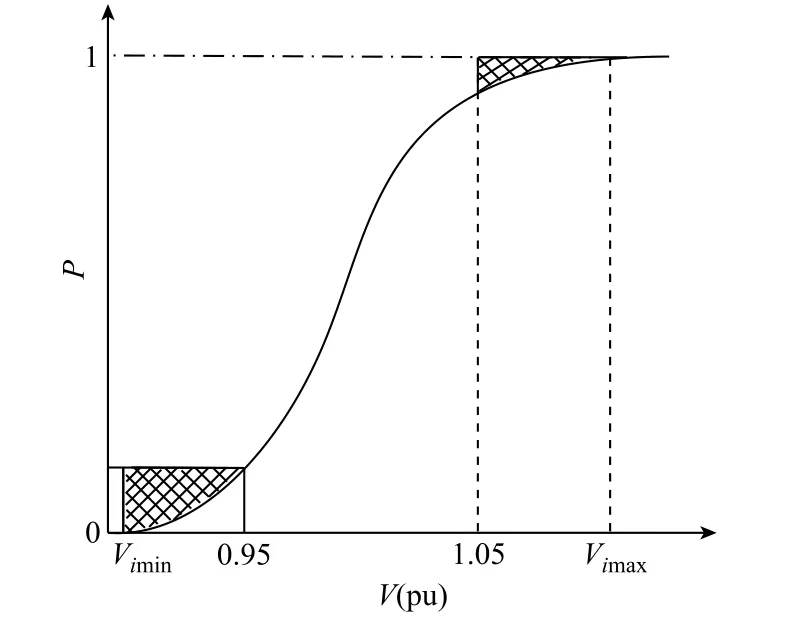
图1 节点电压的CDF 曲线Fig.1 CDF curve of node voltage

3.1.2 支路潮流越限风险指标

与节点电压越限指标相似，但支路潮流只有越上限的风险。支路潮流上限值为线路允许的最大传输功率Pmax，其大小与线路型号有关。支路潮流的越限风险指标计算如下。

若PLmax≤Pmax，支路潮流的越限风险为0；若PLmax＞Pmax，支路潮流的越限风险为

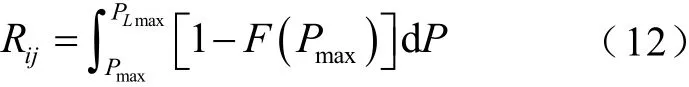
式中，PLmax为某一支路潮流可能出现的最大值；Rij为支路ij的潮流越限的风险。对具有h条支路的电力系统，其支路潮流越限风险指标

3.2 运行风险评估流程

采用本文所提方法进行运行风险评估的具体计算流程如图2 所示。

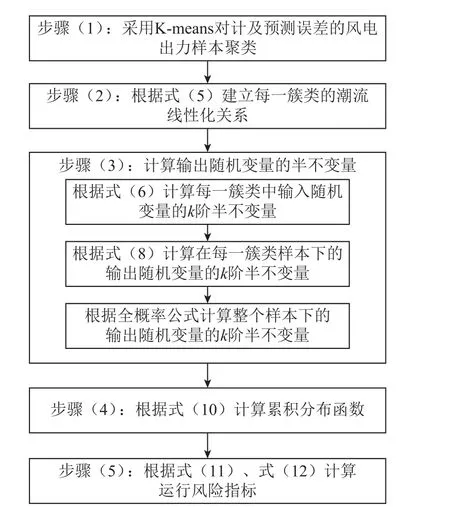
图2 计算流程Fig.2 Compute process

（1）采用K-means 对计及预测误差的风电出力样本聚类。将输入随机变量样本进行聚类，得到a个聚类簇和a个聚类中心。

（2）建立每一簇类的潮流线性化关系。将每一簇类的聚类中心分别代入系统进行潮流计算，确定在每一簇类样本下的潮流线性化关系。

（3）计算输出随机变量的半不变量。首先计算每一簇类中输入随机变量的k阶半不变量，再根据潮流线性化关系计算在每一簇类样本下的输出随机变量的k阶半不变量，最后根据全概率公式计算整个样本下的输出随机变量的k阶半不变量。

（4）计算累积分布函数。利用Gram-Charlier 级数展开理论分别计算节点电压和支路潮流的累积分布函数。

（5）计算运行风险指标。根据累积分布函数计算各节点和支路的越限风险，分别累加各节点和支路的风险值，得到运行风险指标。

4 案例分析

本文选取某实际电网作为算例，基于该算例设定了两种不同场景进行仿真研究。在这两个场景中，场景1 风电并网点为两个，风电装机总量为400MW；场景2 风电并网点为四个，风电装机总量4 000MW。针对上述两个场景而言，本文将场景1 的结果详细列出并进行分析；由于场景2 所采用方法和仿真过程与场景1 一致，且出于篇幅的原因，详细结果和过程本文不再赘述，其得到的风险指标及计算耗时将和场景1 进行对比分析。

4.1 算例系统说明

在该算例系统中，共有810 个节点和977 条支路，其中有263 个负荷节点及48 台发电机，总共负荷为17 400.2MW。系统电压等级有500kV、220kV、110kV、66kV 和35kV 及其以下，图3 的单线图展示了500kV 和220kV 主网架。

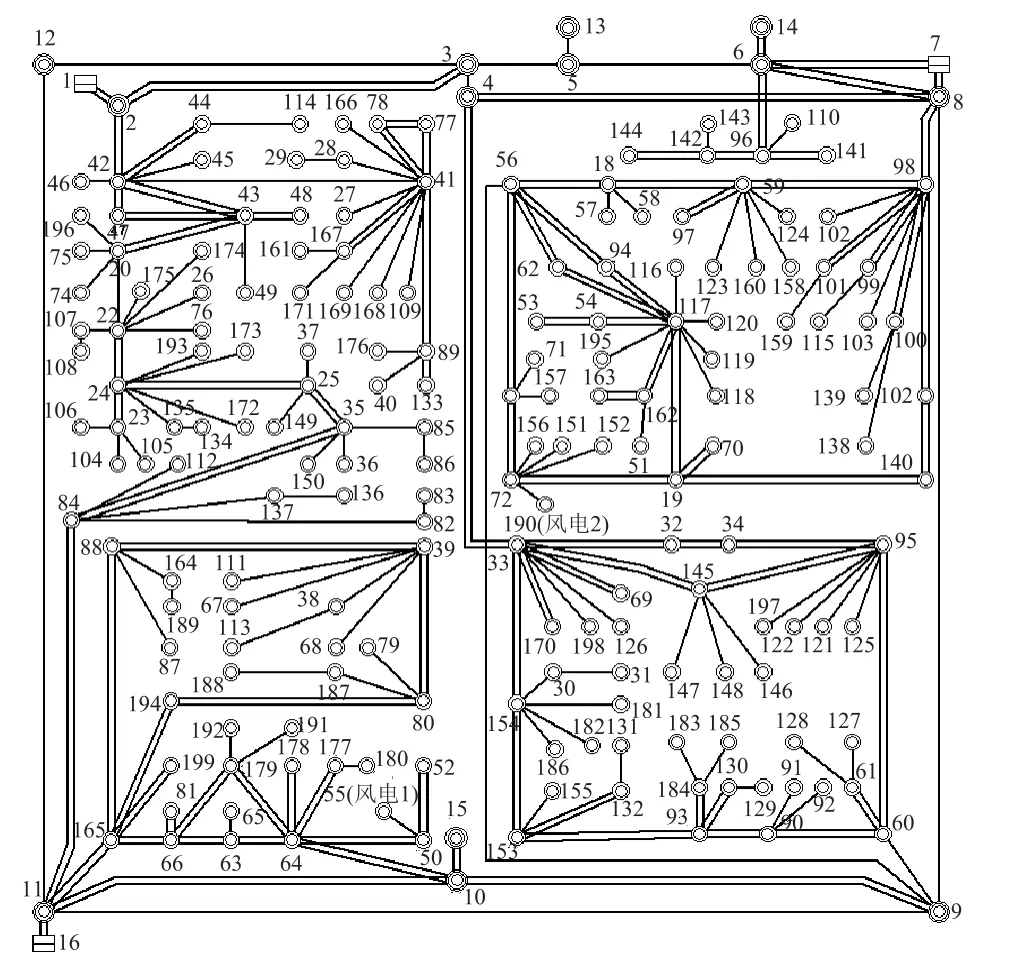
图3 电网单线Fig.3 Single-line diagram of power grid

场景1 中，在220kV 等级的母线55 和母线190 处分别接入装机容量为200MW 的风电场；场景2 中，分别在母线55 和母线190 接入装机容量为200MW 的风电场，将母线7 和母线16 处的火电机组用等容量的风电场代替，故总的装机容量为4 000MW。风场预测误差的概率分布是根据该地区风场实际数据计算而来，选取该地区风电场两年的历史数据（实际功率和预测功率）作为数据支撑，基于上述数据进行统计，计算出适合该地区特性的风场预测误差概率分布。风场预测误差的概率分布通过对所选数据进行数值拟合得到。场景1 中，采用风场实际运行数据进行拟合，得到风场预测误差概率分布为正态分布（拟合结果和比较证明见附录），这也满足了Gram-Charlier 级数展开法对输入数据分布特征的要求。基于此，风场预测误差的概率分布如图4 所示。图4 中分别为节点55 和190 处风电场预测误差的概率分布，风场出力概率分布与其相同。本文将得到的正态分布参与后续的风险评估计算，这样更能反映该地区的实时运行工况。

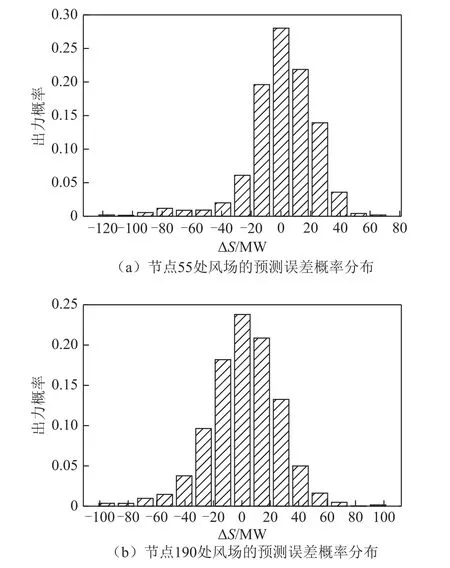
图4 风场预测误差的概率分布Fig.4 Probability distribution of wind farms forecasting errors

4.2 输入随机变量样本的聚类结果

根据图4 的概率分布，采用蒙特卡洛法生成20 000 组符合该分布的样本，使用K-means 对场景1 中两个风场的20 000 组样本进行聚类。对输入随机变量进行聚类时，聚类数量越多效果越好，但耗时较长。因此聚类数量的合理选取不仅可以保证聚类效果，还能提高计算效率。本文使用加权平均半径[21]（Weighted Average Radius, WAR）来确定聚类数目，其表达式为

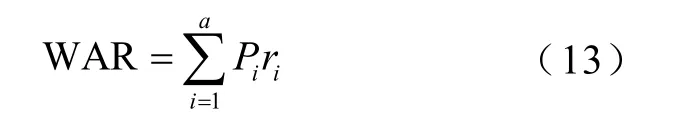
式中，WAR 为聚类后各簇类的加权平均半径；Pi为第i簇类中样本数量占总样本的比例；ri为第i簇类的半径。通过上述计算得出场景1 中WAR 与聚类数量的关系如图5 所示。

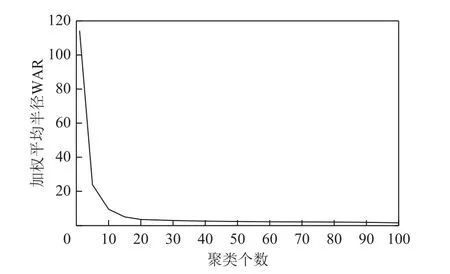
图5 加权平均半径和聚类数量关系Fig.5 Relationship between WAR and number of clusters

根据图5 可知，随着聚类数量的增加，加权平均半径越小，说明聚类的效果越好。从图中可以看出，聚类数量为10 时，WAR 有一个明显的转折；当聚类数量超过20 时，WAR 趋于稳定，且变化较小，因此最佳聚类数量选取应在10～20 之间。基于此，在该区间选取10、12、15、17、19 对比聚类效果，经过对比发现，聚类数量为10 和12 时，对于边缘点聚类效果较差；聚类数量为15、17 和19 时，聚类效果相差较小，考虑到聚类数量和计算耗时成反比的因素，同时在图5 中发现在聚类数量为15 时有一个转折，综合上述几种因素，所以选择聚类数量为15。对输入随机变量样本聚为15 类，其聚类效果如图6 所示。

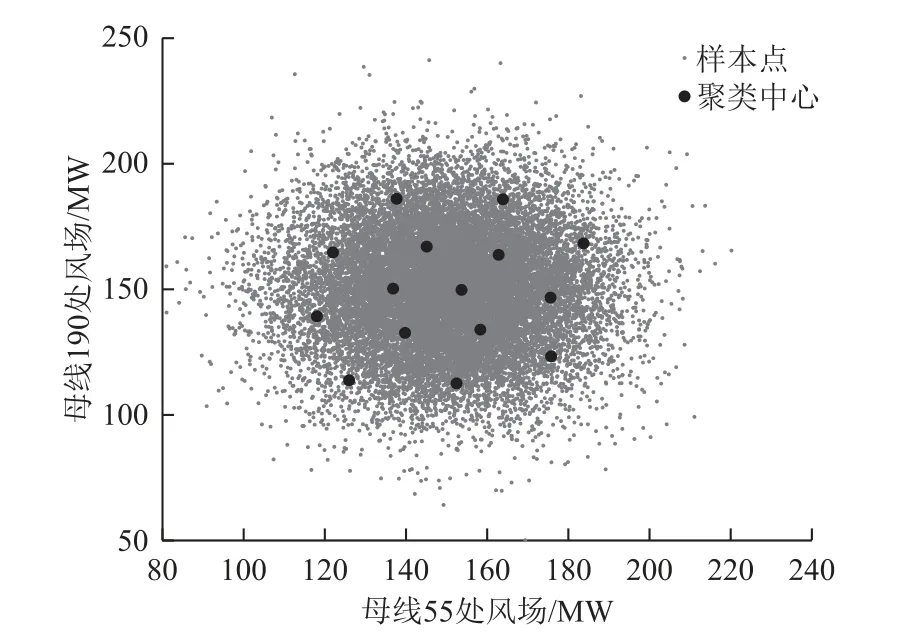
图6 聚类结果Fig.6 Clustering results

在图6 的聚类结果中，15 个聚类中心坐标Mij见表1。

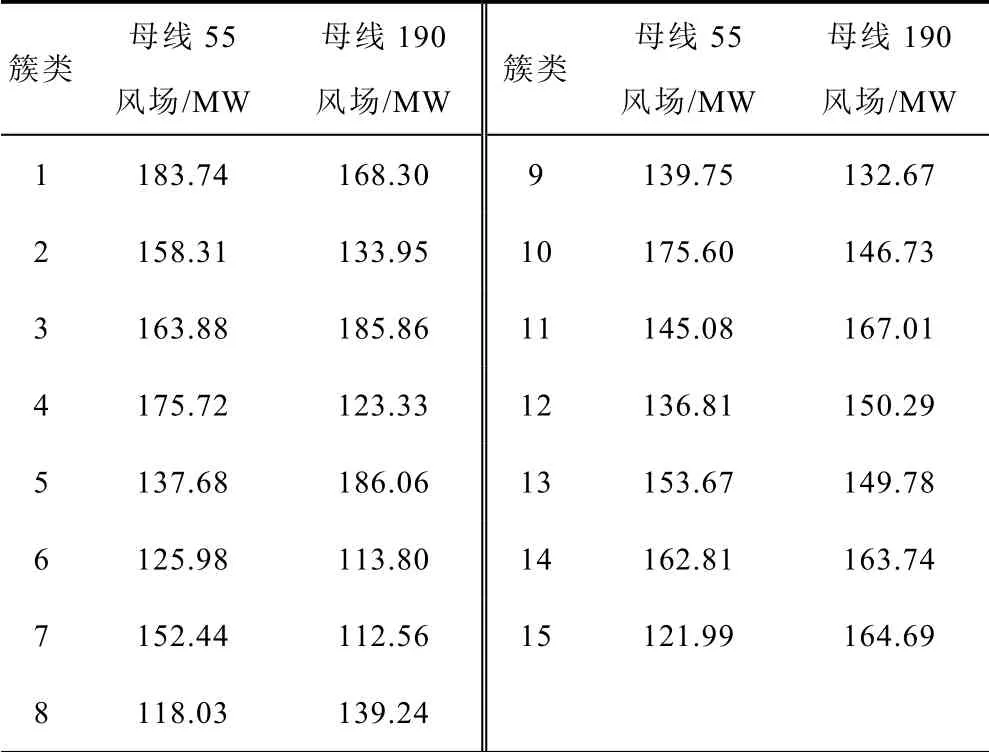
表1 聚类中心坐标Tab.1 Coordinates of the cluster center

4.3 输出随机变量半不变量的计算

根据聚类结果和2.2 节可以计算15 簇类中各类样本对应输入随机变量半不变量、潮流线性化关系和输出随机变量半不变量。由于聚类数目和输出随机变量数量较多，以第15 个簇类样本为研究对象，母线55 处风场注入功率的半不变量见表2。

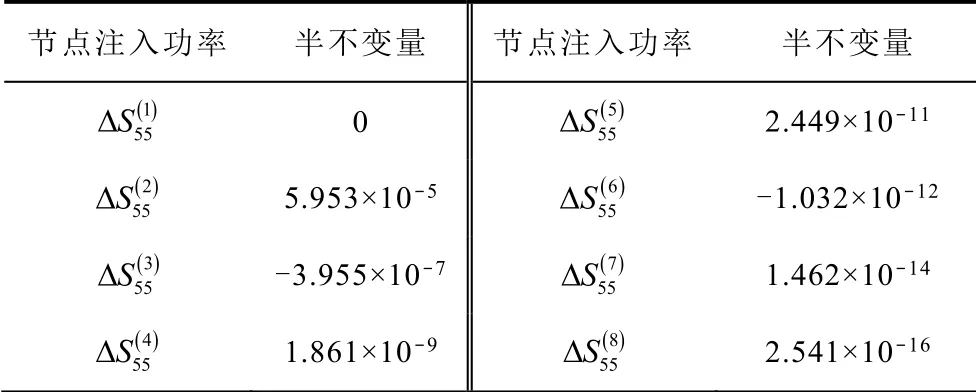
表2 母线55 注入功率的半不变量Tab.2 Cumulant of injected power at bus 55

根据表1 将第15 簇类的聚类中心代入算例系统进行潮流计算，得到该簇类样本对应的潮流线性化关系。以节点190 的电压和支路805 的潮流为例，其线性化关系为

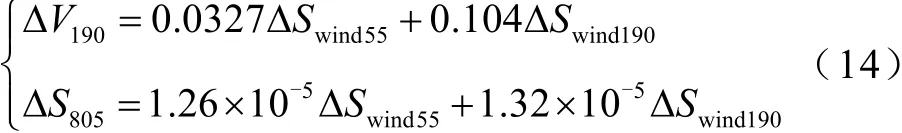
结合表2 和式（14）可以计算该簇类样本对应的节点190 的电压和支路805 的潮流半不变量，见表3。

针对其他簇类而言，将聚类中心Mij代入系统中进行潮流计算，其潮流线性化关系和输出随机变量半不变量均可计算。计算每个簇类样本数量占全样本数量概率见表4。

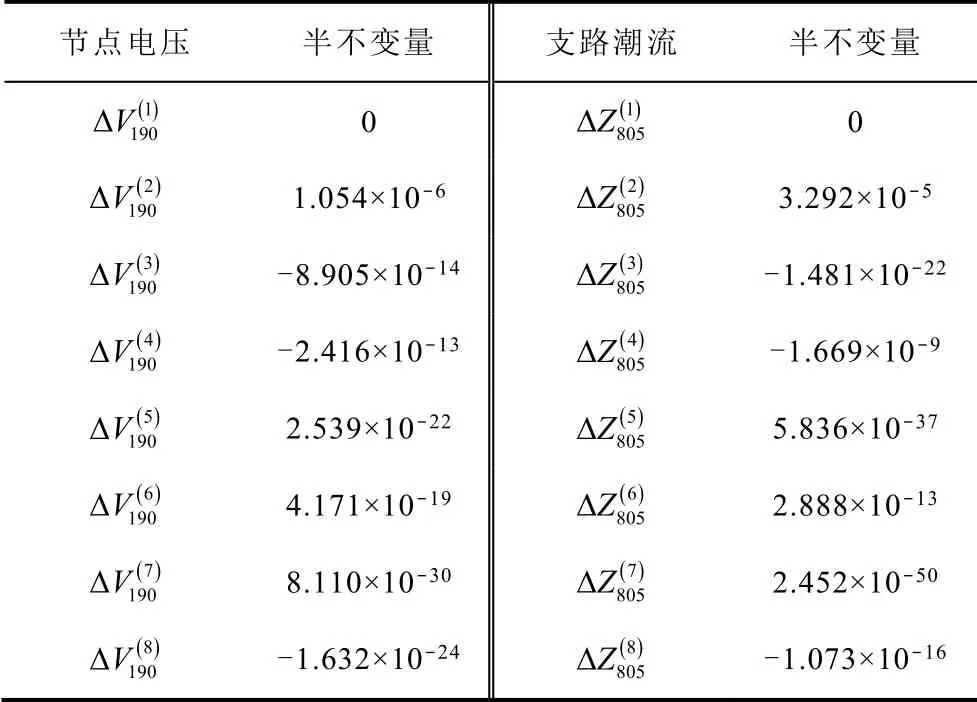
表3 输出随机变量的半不变量Tab.3 Cumulant of output random variable

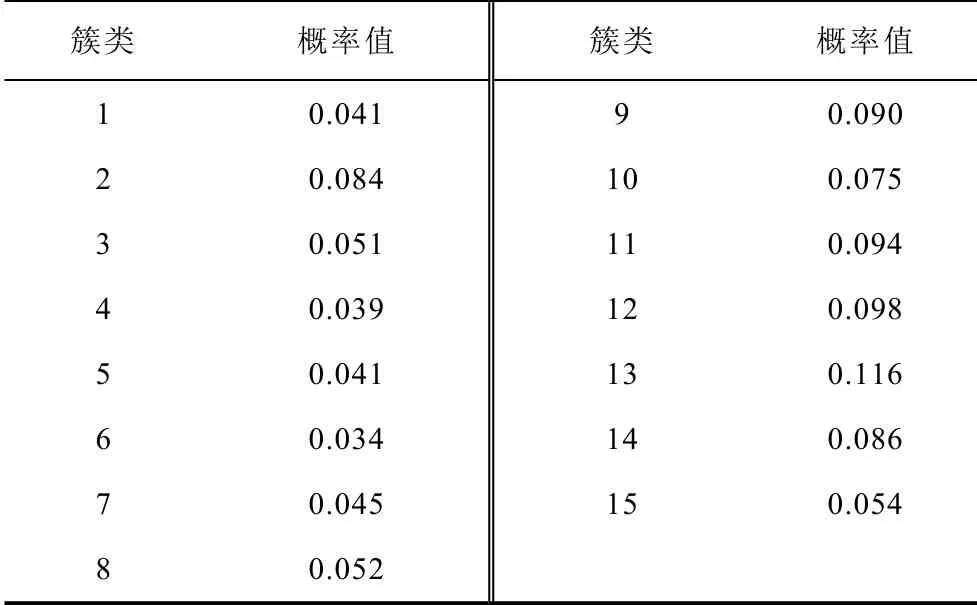
表4 全概率值Tab.4 Total probability value

根据表4 的全概率值计算整个样本下的输出随机变量的半不变量。还以节点190 和支路805 为例，其8 阶半不变量见表5。

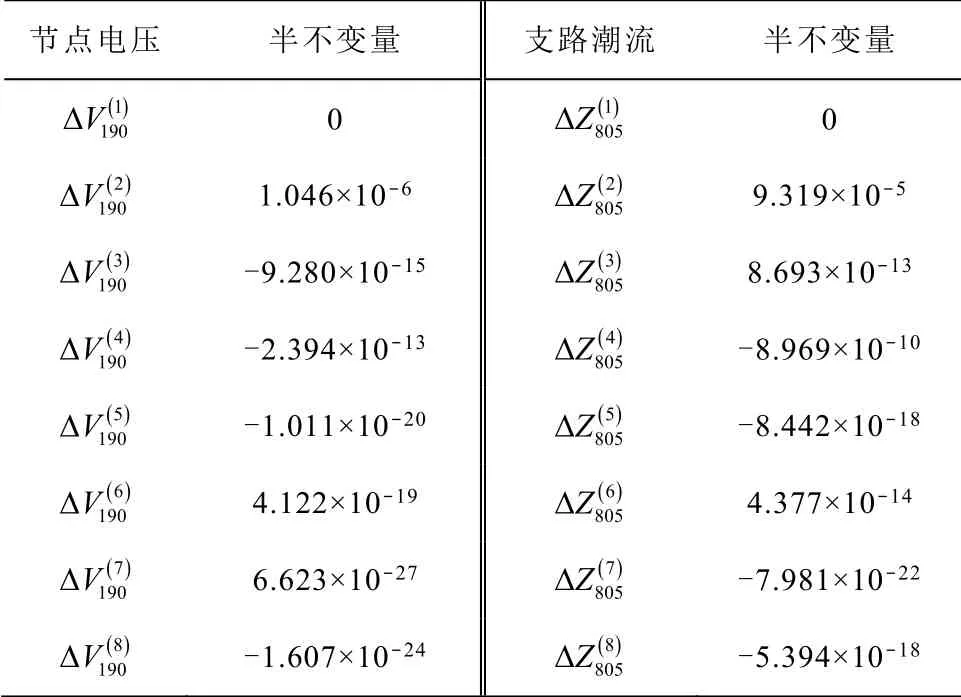
表5 输出随机变量的半不变量Tab.5 Cumulant of output random variable

4.4 输出随机变量累计分布的计算

根据2.3 节中的Gram-Charlier 级数展开理论求得输出随机变量的累积分布，以节点475 和支路544为例，CDF 曲线如图7 所示。

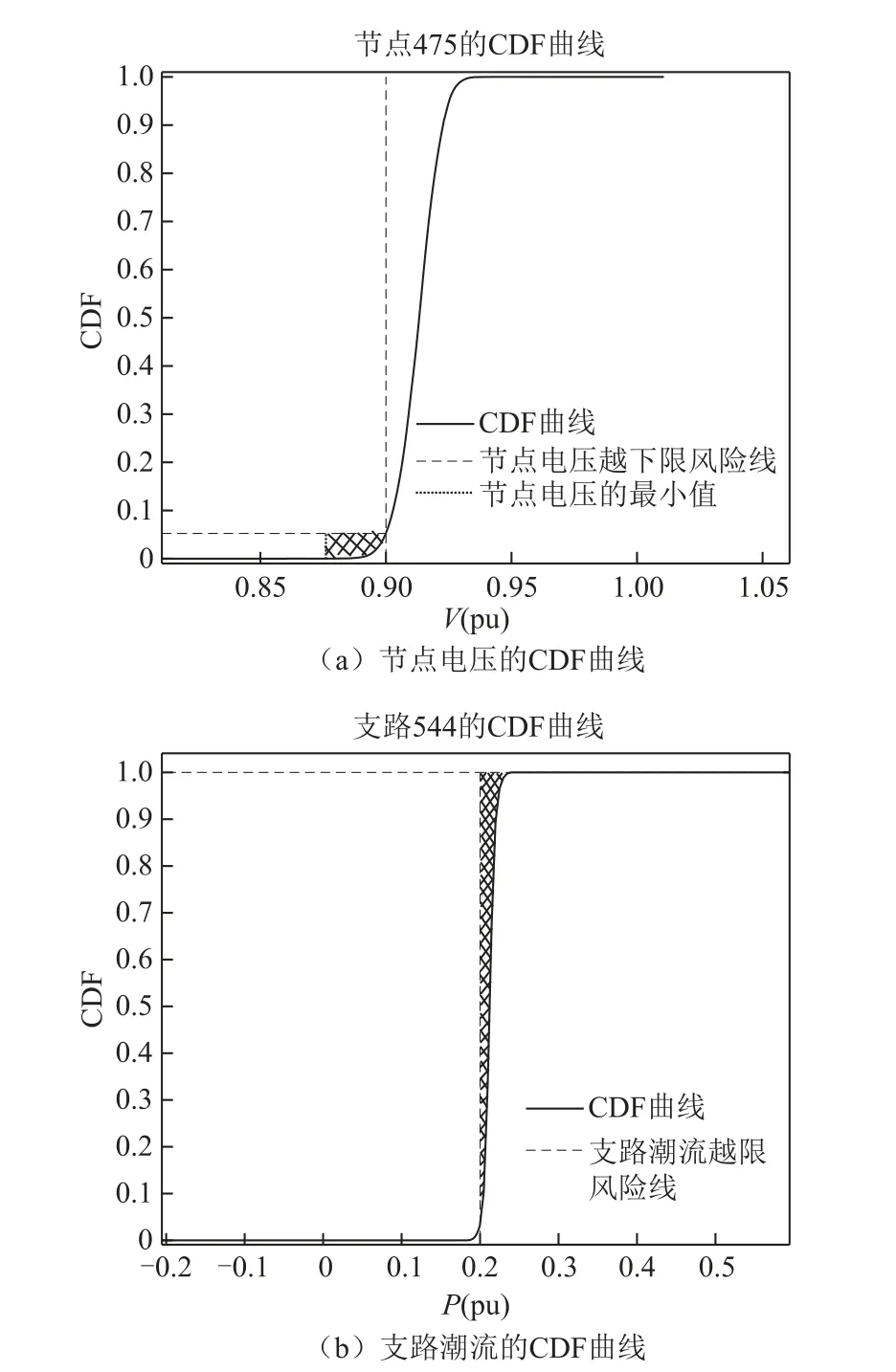
图7 输出随机变量的CDF 曲线Fig.7 CDF curve of output random variable

图7a 中阴影部分面积为节点475 的越限风险值，图7b 中阴影部分面积为支路544 的越限风险值。

4.5 系统运行风险指标

在求得输出随机变量的累积分布的基础上，根据式（11）可以计算各节点电压的越限风险值；同理，各支路潮流的越限风险值也可以由式（12）计算得到。经过计算，场景1 中有121 个节点和9 条支路存在越限风险；经过同样的仿真计算，场景2 中有154 个节点和8 条支路存在越限风险。两个场景运行风险指标见表6。

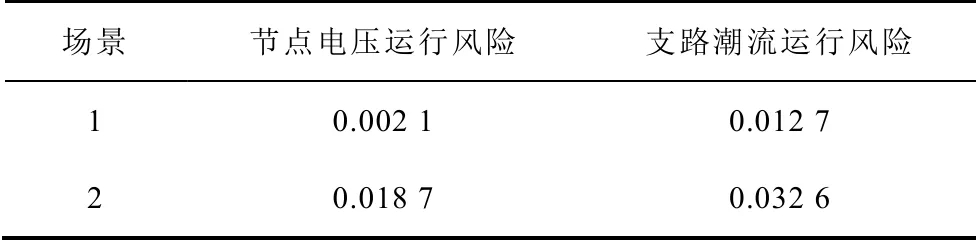
表6 运行风险指标Tab.6 Operational risk indices

从表6 中可见，针对场景1 而言，由于风电波动而引起的节点电压总的风险为0.002 1，支路潮流总的风险为0.012 7；针对场景2 而言，节点电压的总风险为0.018 7，支路潮流的总风险为0.032 6。由此可见，场景2 的节点电压越限风险和支路潮流越限风险均比场景1 大。

4.6 准确性和快速性验证

为了验证本文所提计算运行风险方法的准确性和快速性，与蒙特卡洛法、未聚类的半不变量法和状态枚举法分别进行对比分析。

本文为了保证计算结果的准确性，采用文献[7]中的蒙特卡洛模拟法作为基准与之比较。蒙特卡洛模拟法是根据样本满足相应分布产生大量随机数，在此基础上进行大量重复性潮流计算。由于样本数量足够大，故计算结果足够精准，且不受系统规模的影响，是衡量其他方法准确性的重要参考。因此，本文基于输入随机变量的概率分布，采用蒙特卡洛模拟法生成20 000 组随机数，进行了20 000 次仿真结果作为对比的标准。以节点400 为例，本文方法所得CDF 和蒙特卡洛法的对比见图8。由图8 可见，本文方法的计算结果与蒙特卡洛法吻合度较高，但仍存在一定误差。为了避免偶然性，同时采用了文献[20]中平均方均根（Average Root Mean Square,ARMS）描述两种方法计算结果的误差，经过大量计算（计算结果见附录），结果表明本文提出的方法与蒙特卡洛法相比，误差较小，可以作为随机概率潮流结果。

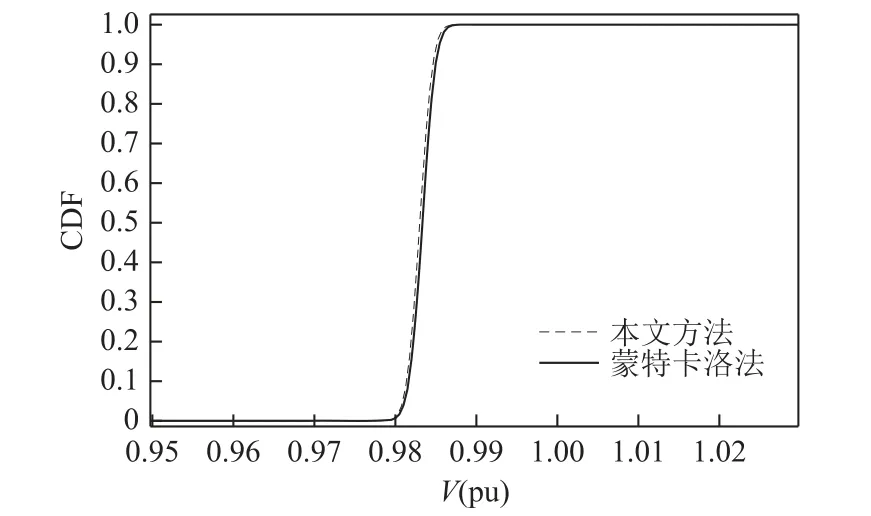
图8 CDF 曲线对比Fig.8 The comparison of CDF curves

同时，本文还采用状态枚举法对系统进行了风险评估。由图4b 可知，场景1 中每个风场有15个出力区间（风场出力区间的选择过程见附录），因此风场出力共有152种组合状态；同理场景2 中风场出力共有 154种组合状态。对两个场景的所有状态进行潮流计算，之后分别计算各个场景的风险指标。

为避免人为主观层面的影响，选取K-means 不同聚类数对计算效率的影响进行验证。分别选取10、12、15、17 和20 个聚类数并使用本文方法进行仿真计算，其耗时结果见表7。

表7 耗时对比Tab.7 Time comparison

由表7 可见，随着聚类数量增加，其耗时在逐渐增加，计算效率会降低（主要原因是聚类数量的增加导致潮流计算的次数增加）。结合之前聚类数量选取的分析，聚类数量选取15 合理。

在基于相同的服务器环境和仿真平台下，对蒙特卡洛法、未聚类的半不变量法、状态枚举法及本文提出的方法分别进行了编译计算，针对两个场景采用上述四种方法的计算用时和风险指标见表8。

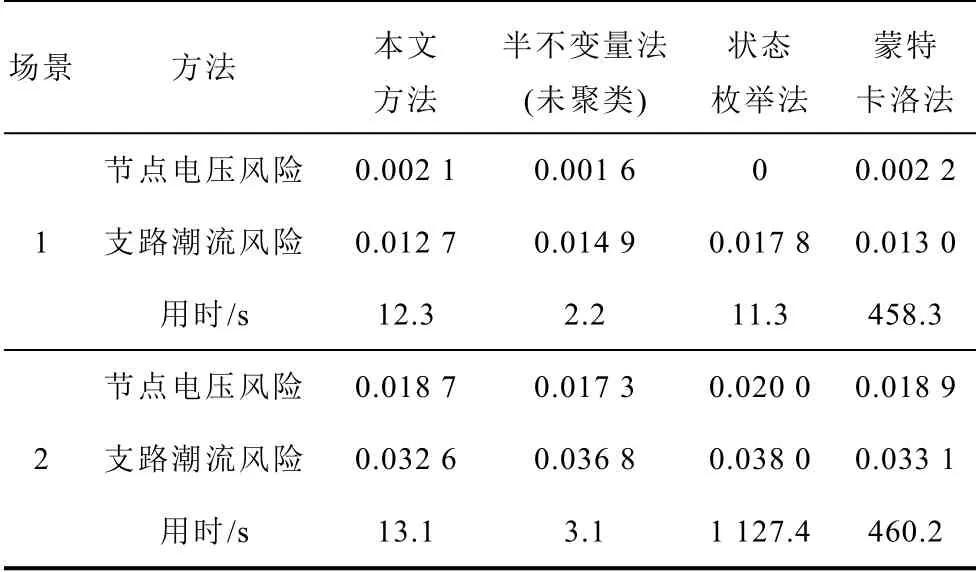
表8 综合对比Tab.8 Comprehensive comparison

表8 中，以蒙特卡洛法的计算结果为标准，在计算的准确度方面，对于场景1，本文方法的准确度为97.4%，半不变量法（未聚类）的准确度为83.6%，状态枚举法的准确度为82.9%；对于场景2，本文方法的准确度为98.6%，半不变量法（未聚类）的准确度为89.8%，状态枚举法的准确度为88.5%。通过两个场景均可以看出，本文提出的方法较半不变量法（未聚类）准确度更高，这是由于采用了聚类技术使得线性化误差大大减小，从而提高了计算精度。综上，本文方法的准确度最高，计算结果与蒙特卡洛法最为接近，证明了本文方法的准确性。

在计算耗时方面，针对场景1 而言，本文方法用时12.3s，仅为蒙特卡洛法的2.68%，其耗时较少的原因有三方面：①本文方法对输入变量样本进行聚类，其聚类数远小于样本数量，因此大大减少了潮流计算次数；②采用本文方法在计算输出随机变量的概率分布时，运用半不变量的方法将卷积运算转换为加法运算，大大降低了计算复杂程度；③根据累积分布计算风险时，仅对越限部分进行统计计算，减少了计算量。半不变量法（未聚类）与本文方法相比，由于只进行一次潮流计算，所以耗时更少，但使用该方法在风电出力波动大的点存在较大的线性化误差，准确度低。状态枚举法耗时11.3s，为蒙特卡洛法的2.47%，与本文方法相差较小。通过对比相同方法下两个场景的耗时情况，发现本文方法、半不变量法（未聚类）和蒙特卡洛法在两种场景下耗时相差很小，但状态枚举法相差非常大，这是由于风电并网点的增加，使系统组合状态数量从152暴增到154，潮流计算量呈指数增长，突显出状态枚举法在处理该种问题上存在一定的弊端。综上所述，通过各方法之间的横向比较和场景之间的纵向比较，可见本文所提方法在计算运行风险时突显其快速性。

5 结论

针对含多个风场的电力系统，本文提出考虑风电预测误差的系统运行风险快速计算方法。其中，K-means 聚类技术的运用有效降低了由风电出力波动性大而导致的线性化误差，在此基础之上，在每一类簇中通过将半不变量法和Gram-Charlier 级数结合，可以准确快速地计算节点电压和支路潮流的概率分布，最后通过积分运算计算运行风险。通过算例分析对本文方法进行了验证，场景1 的结果表明：本文方法计算运行风险比蒙特卡洛法耗时更少，计算效率提高了97.3%；以蒙特卡洛法为标准，与半不变量法（未聚类）和状态枚举法相比，本文方法计算的运行风险准确度最高，达97.4%。

综上所述，采用本文方法进行风险评估，不仅具有高的计算精度，还可大大降低风险评估的耗时，能够满足电力系统实时调度运行在精度和时效上的需求。

附 录

1. 场景1 中，对风场预测误差数据进行拟合，其拟合结果如附图1 所示。

为了验证拟合的精确性，分别计算了附图1a 和附图1b 的ARMS。附图1a 中的ARMS 为7.2×10-4，附图1b中的ARMS 为6.3×10-4，其值均非常小，因此风场预测误差概率分布满足正态分布。

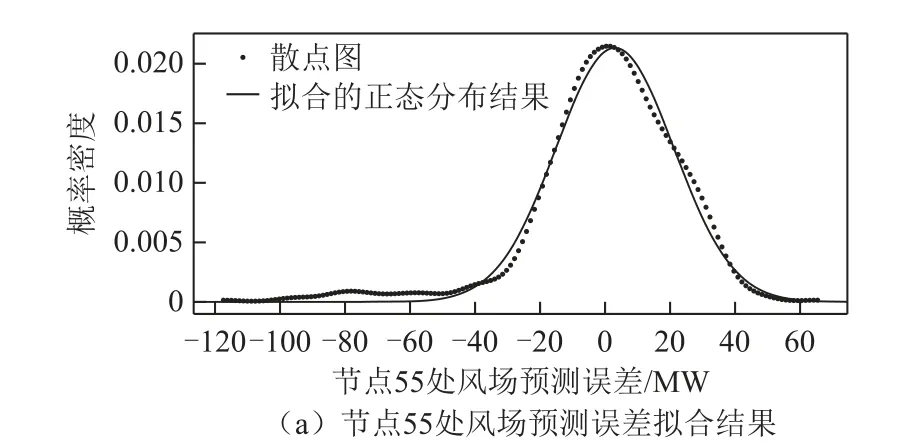
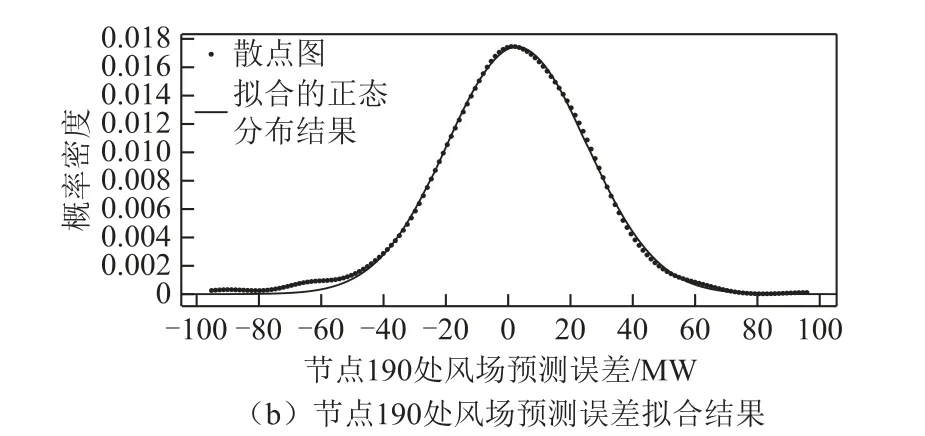
附图1 风场预测误差拟合结果App.Fig.1 Fitting result of wind farms forecasting error

2. 由于本文所选算例规模较大，节点和支路数较多，若全部列出，篇幅较长，因此附表1 中只列出部分数据。

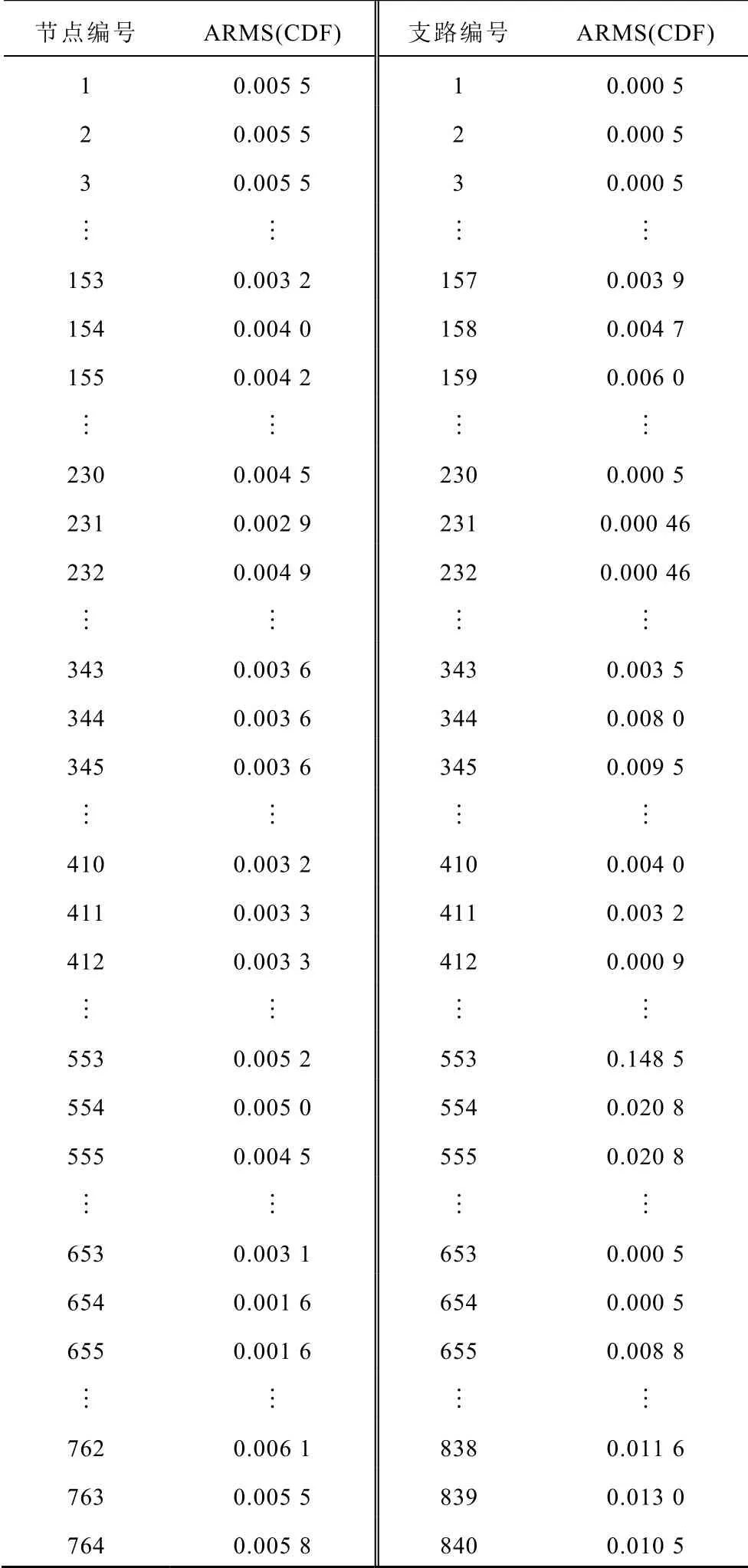
附表1 部分CDF 曲线的ARMS 值App.Tab.1 ARMS value of partial CDF curve

3. 采用状态枚举法计算系统的运行风险时，选取合适的风电出力区间数量，可以节省大量计算时间。分别选取6、8、10、12、15、20、30、40、50、60、70、80个区间进行计算，将各种情况下的耗时和风险值记录于附表2。

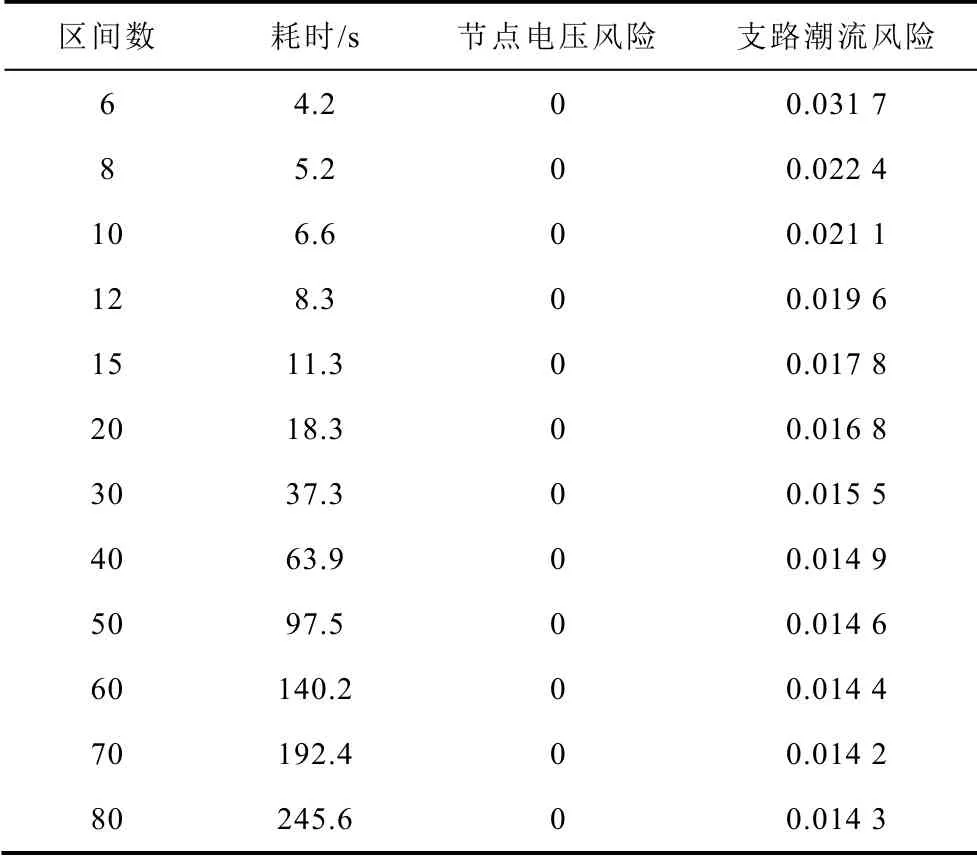
附表2 不同区间的对比App.Tab.2 Comparison of different discrete intervals

基于上述计算结果可见，随着区间数量的增加，其支路潮流越限风险也趋于稳定，但计算耗时在逐渐增加。若选择区间数量较少，计算速度快，但计算结果精度较低；若选择区间数量较多，计算精度可以满足要求，但耗时较长。支路潮流越限风险的均值为0.018 1，观察附表2 中0.017 8 与之最为接近，因此选择区间数量为15。